Lock-up装置的作用机理与分析模型

夏修身，崔靓波，李建中

（1.兰州交通大学土木工程学院，甘肃兰州730070；2.同济大学土木工程学院，上海200092）

Lock-up装置的作用机理与分析模型

夏修身1，崔靓波1，李建中2

（1.兰州交通大学土木工程学院，甘肃兰州730070；2.同济大学土木工程学院，上海200092）

为探讨Lock-up装置的分析模型，介绍了其构造、阐述了其作用机理，给出了Lock-up装置阻尼力的力学模型并提出了相应的数值模拟方法。基于某铁路桥梁，建立全桥有限空间模型，采用文中提出的模拟方法进行了Lock-up装置的减震性能分析，通过与常用的刚性连杆或主从约束模拟方法的比较，明确了刚性连杆模拟方法的适用条件。结果表明，Lock-up装置的地震作用过程比较复杂，当Lock-up装置能够激发出极大的阻尼力时，文中的模拟方法与常用的刚性连杆或主从约束模拟方法结果非常接近，通常情况按刚性连杆或主从约束模拟方法得到的结果偏大。

Lock-up装置；分析模型；地震反应；阻尼力；桥梁

英文文献中常用的冲击传递装置（shock transmission unit，STU）的另一个名字为Lock-up装置（Lock-up device，LUD）［1］。由于该装置传力大小与速度有关，在国内工程上有时也称为速度锁定器。Lock-up装置通常安装在桥梁的伸缩缝或支座附近，在温度作用、收缩和蠕变等低速荷载下的反应很小，不会影响桥梁结构的原有功能；而在地震作用或制动力等高速荷载作用下，装置类似为一个的刚性连接［2］，使结构各个构件共同分担荷载，可用于新建桥梁及旧桥的抗震加固。目前Lock-up装置已在美国Carquinez大桥、孟加拉国Paksey大桥、英国Docklands轻轨铁路桥［3］等得到了应用。

欧洲桥梁抗震规范（2005）中对Lock-up装置低速与高速的参考值、装置的最大承载力、位移能力等参数等有所规定，可以在一定程度上指导设计。尽管我国有多座连桥梁拟采Lock-up装置［4-6］，但现行的铁路、公路及城市桥梁抗震规范中均没涉及Lockup装置，这不利于该装置在我国的应用。国外有关Lock-up装置分析模型的文献很少［7］。国内学者通过简化提出了采用刚性连杆或节点的主从约束近似模拟Lock-up装置的方法［8］，可以满足工程上需要，但是研究中均没有提及到Lock-up装置的关键参数：阻尼系数C值及速度指数a、也很少提涉到Lock-up装置复杂的地震作用机理。

本文阐述了Lock-up装置作用机理，给出了Lock-up装置阻尼力数学模型，提出了分析模型，通过与刚性连杆模拟方法的比较，明确了刚性连杆模拟方法的适用条件。

1 Lock-up装置的构造及作用机理

Lock-up装置与液体黏滞阻尼器具有相同的组成部分，主要由活塞杆、活塞头、圆筒及工作介质几个部分组成［9］，见图1。与阻尼器不同之处是Lock-up装置的活塞孔或壁筒间隙很小，承受较大荷载时仅发生较小位移［10］，除阻尼器常用的液体工作介质外，还可以选择胶泥作为工作介质。由于Lock-up装置所需的位移能力（冲程）较小，它通常都比较紧凑。

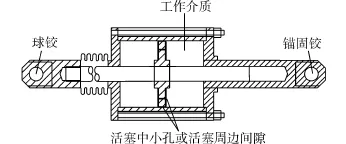
图1 Lock-up装置构造Fig.1 Configuration of Lock-up device

胶泥具有反复触变特性，在低速的温度、收缩和徐变作用下，胶泥受挤压可通过活塞小孔或壁筒间隙。在高速的地震作用或制动力下，胶泥受挤压不能快速通过小孔或壁筒间隙，装置瞬间会产生较大的阻尼力，而仅发生较小的位移，此时装置提供较大阻尼，类似于锁死［11］。

胶泥是硅胶与液体的混合物、容易密封，但胶泥在提供较大阻尼时不能很好的传递热量。当选择液体作为工作介质时，Lock-up装置与阻尼器的工作原理相同［12］：利用黏滞液体通小孔产生阻尼力。与阻尼器相比，低速荷载下液体通过小孔时激发较小阻尼，产生较小的力；而高速荷载下Lock-up装置激发出较大阻尼力。在整个荷载作用过程中，Lock-up装置仅产生较小位移，故其耗能与阻尼器相比较小。

2 Lock-up装置恢复力特性

鉴于Lock-up装置在低速荷载下激发较小阻尼，产生较小的力，高速荷载下装置产生较大力，近于锁死，整个过程耗能较小。文献［8］提出预设一个速度开关V0，在V＞V0时Lock-up装置可按一个刚性连杆计算。锁定力F按下式计算：

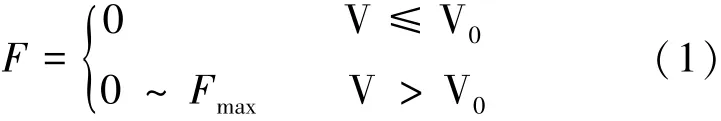
式中：Fmax为最大锁定力。

式（1）中锁定力F随速度V在变化，这如何在有限元分析软件中模拟文献［8］没有说明。文献［4，6，12］采用相连构件平动自由度的主从约束法来模拟Lock-up装置。文献［13］采用大刚度弹簧在通用有限元软件中模拟Lock-up装置。

液体黏滞阻尼器的阻尼力表达式为式中：F为阻尼力，V为活塞速度，C为阻尼系数，a为速度指数。

a与阻尼器的内部构造有关，主要取决孔的大小与形状有关，通常介于0.1～2.0。图2为C＝1 kN·（s／m）的阻尼力与速度函数关系［7］。由图2可以看出，低速荷载下Lock-up装置与阻尼器均输出较小阻尼力，而高速荷载下随着速度的增加Lockup装置输出的阻尼力显著大于阻尼器。文献［7］提出当a＜1时作为液体黏滞阻尼器，当a＞1时用作Lock-up装置。

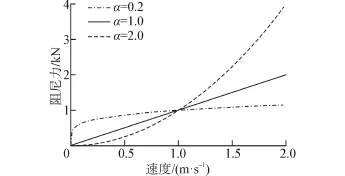
图2 不同速度指数的阻尼力函数关系Fig.2 Force in viscous device against velocity for different values of a

为了考查锁定与解除锁定的速率，文献［14］基于2个幅值57 mm、加载频率为0.001 1 Hz，分别进行了加载速度不大于2.5 mm／s和大约5 mm／s（大于锁定速度）的性能试验，其中一个试验得到的力-位移关系曲线如图3所示，其力－位移滞回曲线与常用的阻尼器力-位移曲线相似［12］。

Lock-up装置利用了阻尼器常用的流动阻抗力技术、采用与阻尼器相同的构造，是一种微冲程阻尼器。当采用刚性连杆或相连构件平动自由度的主从约束方法进行Lock-up装置模拟时不能反应其在地震荷载下大阻尼力、微位移的作用过程。地震作用下只有当Lock-up装置输出的阻尼力与刚性连杆或主从约束连接时产生的水平力相当或相差较小时，采用刚性连杆或主从约束连接才是合理的，否则会过高的估计其锁定效果。因此，采用刚性连杆或主从约束连接模拟Lock-up装置只是工程上的一种简化。

本文建议Lock-up装置的阻尼力采用式（2）计算，为了在高速荷载下产生较大的阻尼力、微小位移、锁定更加有效，建议a取2。相应于式（2）的Lock-up装置恢复力模型可用Maxwell模型［15］模拟，在常用的有限元软件Sap2000、Midas中均有相应的单元模块。

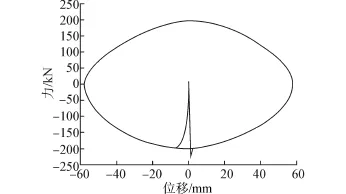
图3 一个冲程的力－位移关系Fig.3 Force vs displacement of a full cycle stroke

3 实例分析

3.1 基本分析数据

某（120＋208＋120）m铁路矮塔斜拉桥，上部结构采取塔梁固结、梁墩分离。下部为圆端形截面空心墩、群桩基础（见图4）。其中1＃墩高为50 m、设置为固定支座，2＃墩高52 m。结构的基本周期为2.018 s、对应振型为1号墩的顺桥向弯曲振动。拟对2＃墩设置8个C＝180 kN·（s／mm）2、a＝2的Lock-up装置，使其与1＃墩共同抗震。桥址位于VII度地震区、II类场地，安评报告给出50年超越概率2%的地震动基本峰值加速度为0.319g。

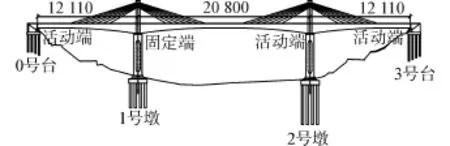
图4 某铁路高墩桥梁的立面布置（单位：cm）Fig.4 Elevation of a typical tall pier railway bridge（unit：cm）

3.2 结构有限元分析模型

借助MIDAS有限元软件，建立空间有限元模型进行顺桥向的地震反应分析。主梁、桥塔与桥墩采用空间梁单元模拟，斜拉索采用空间桁架单元模拟，考虑拉索的垂度效应，修正拉索弹性模量，拉索与主梁及主塔均为主从约束连接。二期恒载为160 kN／m，以分布质量的方式施加到主梁上。桩基础简化成平动、转动及耦联弹簧施加在承台底［16］，土性资料根据m法确定。模型的边界条件列于表1。

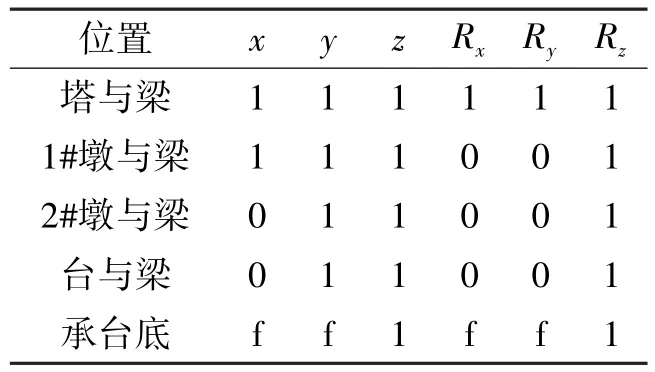
表1 模型边界条件Table 1 Model boundary conditions

为便于分析模型的比较，文中分别采用以下2种方法模拟2＃墩的Lock-up装置。

方法1：采用Maxwell模型、连接弹簧刚度文中取2×108kN／m，输入表1中的参数；

方法2：墩、梁平动自由度的主从约束［4，12］。

3.3 结果及分析

以50年超越概率2%的安评地震波作为地震动输入（见图5）。采取（顺＋竖）的地震动输入方式，竖向地震动幅值取水平地震动的0.65倍［16］。图6～11及表2为图5所示安评地震波的分析结果。

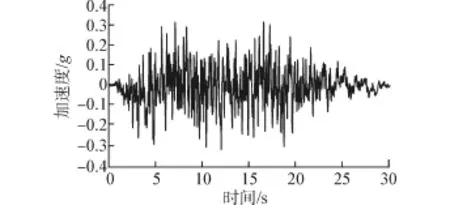
图5 安评地震动Fig.5 Seismic safety assessment acceleration wave

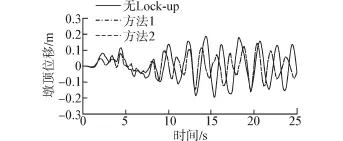
图6 1＃墩顶水平位移时程曲线Fig.6 Top displacement time-history for pier No.1

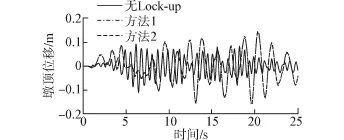
图7 2＃墩顶水平位移时程曲线Fig.7 Top displacement time-history for pier No.2

由图6、7可以看出，Lock-up装置显著减小了1＃墩顶的水平位移、增大了2＃墩顶的水平位移。这是因为通过Lock-up装置使得1＃墩与2＃墩共同抗震、2＃墩分担了1＃墩的部分地震作用。由表2可知，与无Lock-up装置相比，1＃墩顶位移按方法1模拟时减小了17%，而按方法2模拟时减小了15%；至于2＃墩顶位移按方法1模拟增大了55%，按方法2模拟则增大了58%。2个方法所得的1＃、2＃墩顶位移时程曲线基本重合。由图8、图9及表2可知，与墩顶位移相似、墩底弯矩也有此规律。

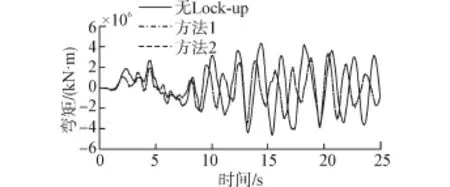
图8 1＃墩底弯矩时程曲线Fig.8 Base moment time-history of pier No.1

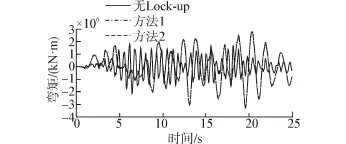
图9 2＃墩底弯矩时程曲线Fig.9 Base moment time-history of pier No.2

尽管地震过程中两者的作用机理不同，但对于文中算例，方法1模拟Lock-up装置的分析结果与方法2比较接近（略小于方法2的结果），且时程反应曲线基本重合。原因是2＃墩顶所有的Lock-up装置激发出阻尼力之和为73 138 kN比刚性连杆模拟时墩顶的水平力73 909 kN仅小1%（见表2），这说明Lock-up装置接近刚性连杆，所以两者结果比较接近。方法1模拟结果小于方法2是由于方法1模拟时能够充分考虑到Lock-up装置作用机理，方法2有一定的简化。Lock-up装置激发的阻尼力与活塞速度的平方成正比，地震中活塞速度时刻在变，按方法1模拟时梁部与2＃墩之间类似为变刚度的弹性连接、结构的自振周期会随着连接刚度变化而变化。高速荷载下2＃墩与梁之间类似刚性连、其位移小耗能相对很小；介于低速荷载与高速荷载之间时Lockup装置也有一定的耗能能力（见图10）。而方法2墩梁按刚性连杆连接会减小结构周期、从而增大结构总的地震反应［11］，2＃墩分担值较方法1也会增大。由图10可以看出，当阻尼系数为180 kN·（s／mm）2时，Lock-up装置的最大锁定位移约为6 mm（相对于常用的阻尼器而言其耗能能力较小、可忽略不计），但Lock-up装置耗散了小部分能量也会使方法1的结果小于方法2。

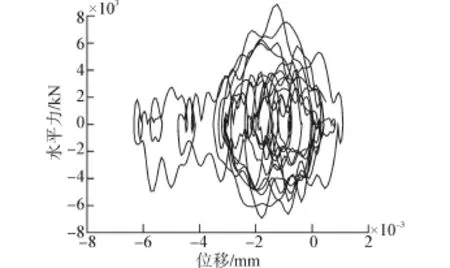
图10 Lock-up装置的力-位移关系曲线Fig.10 Load-displacement hysteretic curve of LUD

为了进一步讨论模拟方法1、方法2，仅调整表1中的阻尼系数C。C值是Lock-up装置的重要参数，由前文的Lock-up装置作用机理知，它决定输出阻尼力，对地震反应有较大影响。以下分析中C的取值没有考虑现有技术能否加工生产。

图11、图12及表3是不同C值下方法1模拟Lock-up装置的分析结果。

由表3可以看出，该桥的地震反应随C值的增大而增大。这是因为其他参数不变的情况下，C值增大，就是输出阻尼力的增大，即墩梁之间连接的加强，这会减小结构周期从而增大结构总的地震反应。由图11、图12及表2、表3可以看出，C值越大，方法1的结果越接近方法2的结果。当C＝1 800 kN·（s／mm）2时，方法1的1＃墩底弯矩比方法2的小0.5%，2＃墩的小0.2%。这验证了墩梁之间的Lock-up装置输出阻尼力足够大时，用方法2模拟比较合理；同时也表明，通常情况下用方法2模拟Lock-up装置得到的结果偏大，在工程上是偏于安全的。

由表2及图11可以看出，当C＝1.8 kN·（s／mm）2（常用阻尼器的阻尼系数C取值范围）时，2＃墩顶Lock-up装置输出的总阻尼力为65 273 kN比方法2的墩顶水平力73 909 kN小12%，两者相差较大。此时对于1＃墩底弯矩方法1的结果比方法2小17%，2＃墩底弯矩则前者比后者小13%；与C＝1 800 kN·（s／mm）2相比，两者的时程曲线也差别较大。这也进一步验证了只有布置足够多的Lockup装置或其阻尼系数取值较大能够激发出极大的阻尼力时，常用的刚性连杆或主从约束模拟Lock-up装置才比较合理。笔者分析中还输入了其他2条安评地震波，也有类似规律、其结果文中没有单独列出。

表2 桥墩地震反应Table 2 Seismic response of the piers

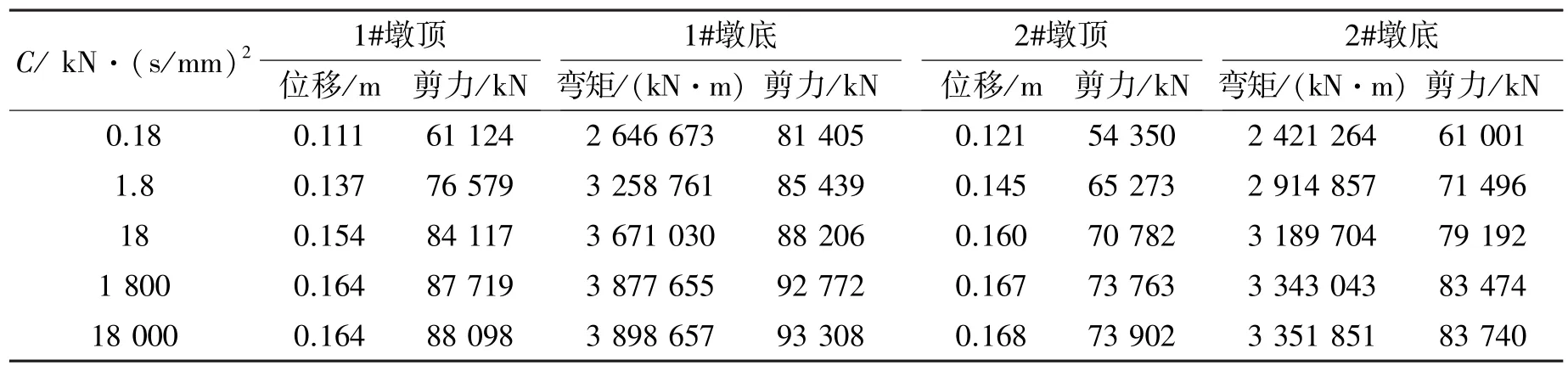
表3 不同C值的桥墩地震反应Table 3 Seismic response of the piers vs value C

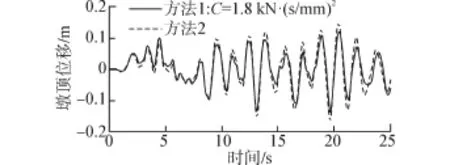
图11 1＃墩顶水平位移时程曲线比较Fig.11 Top displacement time-history for pier No.1

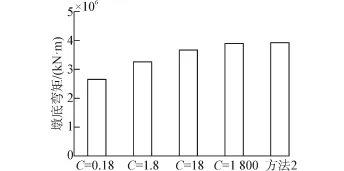
图12 1＃墩的墩底弯矩Fig.12 Base moment time-history for pier No.1

4 结论

1）基于Lock-up装置的作用机理，给出了其阻尼力的力学模型，并提出了相应的模拟方法。

2）当Lock-up装置能够激发出极大的阻尼力时，文中的模拟方法与常用的刚性连杆或主从约束模拟方法结果非常接近。

3）Lock-up装置的地震作用过程比较复杂，按刚性连杆或主从约束模拟方法得到的结果偏大，工程上设计中采用时偏于安全。

4）Lock-up装置的阻尼系数C对地震反应有较大的影响，分析中只有采用较真实的C值才可能得到较“精确”地震反应值。

［1］STEPHEN B D.Bridge strengthening with shock transmission units［C］／／11th World Conference on Earthquake Engineering.Acapulco，Mexico，1996：1849.

［2］EN 1998-2，Eurocode 8-design of structures for earthquake resistance-Part 2：Bridges［S］.［S.l.］，2005.

［3］PATEL D J.Value of shock transmission units for Mumbai Bridge［C］／／Proceedings of the Institution of Civil Engineers.Mumbai，India，2004：203-212.

［4］王磊，刘寒冰，吴斌喧，等.新型地震结构保护系统的大跨径桥梁抗震分析［J］.哈尔滨工业大学学报，2004，36（12）：1665-1668.WANG Lei，LIU Hanbing，WU Binxuan，et al.Seismic response analysis for long span bridge with new earthquake protective system［J］.Journal of Harbin Institute of Technology，2004，36（12）：1665-1668.

［5］张永亮，陈兴冲，颜志华.Lock-up装置在连续梁桥上的减震性能研究［J］.世界地震工程，2010，26（2）：48-52.ZHANG Yongliang，CHEN Xingchong，YAN Zhihua.Research on seismic reduction performance of lock-up device applied to continuous girder bridge［J］.World Earthquake Engineering，2010，26（2）：48-52.

［6］曾武华，孙海朋，卓卫东.早期大跨径连续梁桥改造中的抗震方案比选［J］.福州大学学报：自然科学版，2013，41（4）：505-509.ZENG Wuhua，SUN Haipeng，ZHUO Weidong.Seismic scheme comparison in reconstruction design of an early longspan continuous girder bridge［J］.Journal of Fuzhou University：Natural Science Edition，2013，41（4）：505-509.

［7］DION C，BOUAANANI N，TREMBLAY R，et al.Realtime dynamic substructuring testing of viscous seismic protective devices for bridge structures［J］.Engineering Structures，2011，33（12）：3351-3363.

［8］陈永祁，耿瑞琦，马良喆.桥梁用液体黏滞阻尼器的减振设计和类型选择［J］.土木工程学报，2007，40（7）：55-61.CHEN Yongqi，GENG Ruiqi，MA Liangzhe.Design and selection of fluid viscous devices for shock control of bridges［J］.China Civil Engineering Journal，2007，40（7）：55-61.［9］BROWN W M，RAY N，MANDAL A.TechStar lock-up devices＆anti-seismic expansion joints in Southern Asia［C］／／IABSE-JSCE Joint Conference on Advances in Bridge Engineering-II.Dhaka，Bangladesh，2010：360-365.

［10］康斯坦丁诺.桥梁地震保护系统［M］.陈永祁，马良喆，译.北京：中国铁道出版社，2012：218-224.

［11］王志强，葛继平.粘滞阻尼器和Lock-up装置在连续梁桥抗震中应用［J］.石家庄铁道学院学报，2006，19（1）：5-9.WANG Zhiqiang，GE Jiping.Application of viscous damper and lock-up devices in the seismic design of continuous girder bridges［J］.Journal of Shijiazhuang Railway Institute，2006，19（1）：5-9.

［12］陈永祁.桥梁工程液体黏滞阻尼器设计与施工［M］.北京：中国铁道出版社，2012：46-54.

［13］聂利英，李建中，胡世德，等.西堠门大桥3种梁端约束体系比较［J］.桥梁建设，2006（6）：73-75.NIE Liying，LI Jianzhong，HU Shide，et al.Comparison of three kinds of girder end constraint systems for Xihoumen Bridge［J］.Bridge Construction，2006（6）：73-75.

［14］CASTELLANO M G，COLATO G P，INFANTI S.Use of viscous dampers and shock transmission units in the seismic protection of buildings［C］／／13th World Conference on Earthquake Engineering.Vancouver，Canada，2004：2172.

［15］叶爱君，范立础.附加阻尼器对大跨度斜拉桥的减震效果［J］.同济大学学报：自然科学版，2006，34（7）：859-863.YE Aijun，FAN Lichu.Seismic response reduction of a super-long-span cable-stayed bridge by adding dampers［J］.Journal of Tongji University：Natural Science Edition，2006，34（7）：859-863.

［16］GB50111-2006铁路工程抗震设计规范［S］.北京：中国计划出版社，2009.

Mechanism and analysis model for a lock-up device

XIA Xiushen1，CUI Liangbo1，LI Jiangzhong2
（1.School of Civil Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China；2.College of Civil Engineering，Tongji University，Shanghai 200092，China）

The configurations and mechanism of a lock-up device（LUD）are presented for investigating its analytical model.Mechanical model of damping force for LUD is given，and the corresponding numerical simulation method is proposed.Based on a railway bridge，the finite element model of the bridge is established.The seismic performance analysis is performed by using the above-mentioned simulation method for LUD.Applicable conditions for rigid rods or master-slave constraints method are defined by comparing with the common methods such as rigid rods or master-slave constraints.The results showed that the seismic process of LUD is quite complicated.When the LUD can inspire great damping force，the seismic results by the simulation method proposed in this paper are very close to the conventional rigid rods or master-slave constraints.Usually，the results obtained from rigid rods or masterslave constraints are too large.

lock-up device；analytical model；seismic response；damping force；bridge

10.3969／j.issn.1006-7043.201309007

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201309007.html

U442

A

1006-7043（2014）12-1497-06

2013-09-02.网络出版时间：2014-12-02.

国家自然科学基金资助项目（51368033）；长江学者和创新团队发展计划资助项目（IRT1139）.

夏修身（1978-），男，副教授，博士；李建中（1963-），男，教授，博士生导师.

夏修身，E-mail：xiaxiushen＠mail.lzjtu.cn.