中国股票市场牛熊市运行周期探究

闫 超 刘金全 隋建利

中国股票市场牛熊市运行周期探究

闫 超 刘金全 隋建利

本文运用马尔科夫区制转移模型描述和研究中国股票市场综合指数日收盘价序列的动态轨迹，以此来研究中国股市的牛、熊市周期。实证结果表明，上证和深证综合指数日收盘价在不同的区制状态下均可以表现出较为显著的持续性特征，上证和深证的牛、熊市区间具有明显的协同性。同时发现，中国的经济政策操作与股票市场价格波动及股票市场区制的阶段性转变之间具有明显的相关性。

股票市场 牛市 熊市 马尔科夫区制转移模型 平滑概率

一、引言

中国股票市场自1991年正式运行以来，经历了二十多年的跳跃式发展，无论是上市公司数量、投资者数量，还是成交量、交易金额及筹资规模等都实现了快速攀升。然而，中国股票市场依旧是新兴投资市场，受到多方面非经济因素干扰，投资者大多具有情绪化非理性投资的行为，市场内投机行为较泛滥，股票价格波动剧烈。所以中国的股票市场还不成熟，还有待成长理性，这就使得对中国股票市场的研究更具有必要性。近年来资本市场风险管理理论、投资组合理论等研究理论的迅猛发展，使得股票价格走势的内在机制及其伴随的价格预测、风险评估、投资组合等研究领域成为学者们的关注热点。

对于股票市场的每一个参与者和监管者而言，了解股票市场的现状和运行规律尤为重要。首先，中国股票市场目前存在市场格局不稳定，开放性程度较拘谨，监管制度不完善，投资者结构不合理等一系列问题。市场体系的局限性无疑会影响股票市场的运行进程和状态，因而要基于市场波动的幅度和持续时间等指标探寻股票市场的完善方案，以此把握股票市场的运作脉搏。其次，对于投资者而言，股市周期的扩张和收缩能够折射出经济态势、政策变化及整个行业的兴衰繁荣。只有把握市场的周期变化，才能更深入地了解股票市场的发展形势，据此制定适合投资者的投资策略，规避市场风险。众所周知，股票市场是宏观经济的“晴雨表”，股票指数更是众多宏观经济变化征兆中无可替代的指标，针对股票市场的牛、熊市进行探究，将更为清晰地对宏观经济作出合理预期。

股票市场通常有“牛市”和“熊市”之分。对股票市场周期的划分就是对其牛熊市周期的划分。如何准确地划分股票市场的牛市和熊市，特别是对于牛熊市转折时期的辨认与确定是学者们努力研究的重点。在过去的几十年里，国内外学者对股票市场周期的研究已取得了一定的结果。伯恩斯和米切尔（Burns＆Mitchel，1946）［1］专门研究了股票市场周期测定方法，提出了将一个完整的经济周期分成九个标准阶段的技术方法，并且认为通过分析价格指数的趋势变化可以确定经济周期转折点，这项研究为牛市和熊市转折点的确立奠定了根基。霍德里克和普雷斯科特（Hodrick＆Prescott，1997）［2］借助滤子平滑处理的方法研究了股市周期。坎贝尔等（Campbell et al，1997）［3］认为股票回报会随着时间的变换发生状态转移，这对于后人诊断牛市和熊市奠定了基础。马休和麦柯迪（Maheu＆McCurdy，2000）［4］采用马尔科夫区制转移模型对美国股票市场进行周期划分，他们认为牛市具有高回报、稳定状态的特征，而熊市被定义为低回报、不稳定状态。佩根和索斯诺维（Pagan＆Sossounov，2003）［5］认为在划分牛熊市时应该考虑市场交易状况，并对BB法则进行修正来确定转折点。而艾德瓦兹等（Edvards et al，2003）［6］应用非参数法划分股市的牛市和熊市。比斯盖瑞和格雷西亚（Biscarri＆Gracia，2004）［7］研究了西班牙股市于1941～2002年的牛熊市，及牛熊市的特征表现，并将西班牙股市周期特点与美国和欧洲发达国家比较判断，得出西班牙股市与发达国家具有较强的一致性的结论。冈萨雷斯等（Gonzalez et al.，2005）［8］等人论述了牛、熊市的转折点及其股市周期持续阶段，并且阐释了牛市与投资回报之间的关系。

进入21世纪以来，中国的股票市场经历了多个明显不同的阶段，股价升则迅猛上涨，屡创新高；降则一路低迷，持续下跌。尤其是2005～2007年，中国股票市场自开市以来创下了最高的上涨记录。如此变化多端的股市，其股票市场牛熊市周期是怎样的呢？中国学者对于中国股票市场的牛熊市周期进行了研究。孟卫东等（2000）［9］运用统计量分析方法探究了上海股市，发现其具有很强的星期效应。朱战宇等（2003）［10］认为为避免造成统计上的偏差，应选择完整的样本周期作为检验对象。黄继平和黄良文（2003）［11］利用波谱分析方法分解出股市波动的各个周期。陆蓉和徐龙炳（2004）［12］借助波浪理论划分股票市场波峰及波谷，进而区分牛、熊市。何兴强和周开国（2006）［13］探讨了中国股市周期及股市间的周期协同性，研究发现中国股市价格服从随机游走过程。夏南新（2006）［14］利用分形技术发现上证综指日收益序列的统计循环长度大约是270天。周孝华和黄赟（2008）［15］对中国沪深股市的波动性进行研究，发现沪深两市场波动周期相互影响。郝梅瑞和周观君（2006）［16］根据中国新股收益状况得出中国A股市场具有周期波动规律的结论。祖垒等（2011）［17］应用H－P滤子平滑处理股指后进行了牛熊市的划分。

虽然已有众多学者对于中国股票市场的牛熊市周期进行了研究，然而目前鲜有学者使用马尔科夫区制转移模型来探讨中国股市牛、熊市划分的相关问题。近年来，在宏观经济和金融体系的研究领域中，该模型已被学者们广泛使用。瑞思和派瑞（Rence＆Perron，1996）［18］运用马尔科夫区制转移模型探究了中国股市，研究表明中国股市具有显著的结构性变化特征。近年来，金融学术界运用区制转移模型探讨中国经济各个领域的文献逐步增多。刘金全和郑挺国（2006）［19］分析了利率期限结构的区制转移模型；龙如银等（2005）［20］以及刘金全等（2009）［21］分别利用马尔科夫区制转移模型研究了中国通货膨胀率变化的动态行径；刘金全和刘志刚（2006）［22］以及张小宇和刘金全（2012）［23］利用马尔科夫区制转移模型探索了中国经济周期的区间划分；李敏等（2010）［24］探索了人民币有效汇率变动的动态行为；蒋祥林和李一凡（2011）［25］分析了中国短期利率的动态特征。

本文基于马尔科夫区制转移模型来划分中国股票市场的牛熊市周期，目的在于发现其内在规律，帮助投资者了解其真实的市场运作态势，这对于完善中国股票市场机制，促进其良好稳定发展具有理论价值和现实意义。

二、马尔科夫区制转移模型的构建及其参数估计

通常情况下，在研究经济或金融时间序列动态行为特征的过程中，所使用的方法就是建立时间序列的自回归模型，旨在考察不同时期所研究时间序列数据之间的相互依赖程度，并且检验该自回归模型对时间序列历史数据的拟合效果。因此，为了科学准确地进行中国股票市场牛熊市周期划分，在此我们将沪深股市综合指数日收盘价序列｛πt｝的自回归模型表示为：

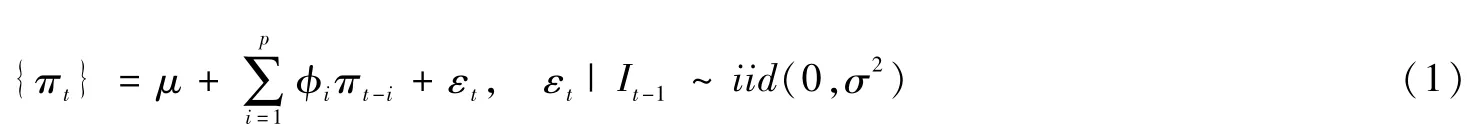
其中，It－1代表t－1期以前的信息集。假设方程（1）中所涵括的回归系数以及误差分布的均值和方差都是恒定不变的常数，这就是说，当期的股市综合指数日收盘价，其实能够依赖于前p期的股市综合指数日收盘价，即方程（1）所示的自回归模型能够具体刻画股市综合指数日收盘价路径所具有的平稳性特征，然而，该简单的自回归模型并不能完全线性刻画带有结构突变性质的时间序列，而具有结构突变性质的时间序列就是指在其动态变化的过程中，其波动程度呈现非线性特征。如果依旧使用方程（1）所示的线性向量自回归模型，将会导致最终的实证结果误差偏大。换句话说，该简单的自回归模型不能准确严谨地反映股票市场牛、熊市的数据生成过程。

根据上述分析，并参考汉密尔顿（Hamilton，1989）［26］的观点，在构建上文所设定的简单自回归模型（1）的基础之上，进一步考虑包含马尔科夫区制转移形式的股市综合指数日收盘价模型：

其中，当区制状态变量St＝i，i＝1，2时，Sit＝1且Skt＝0，k≠i。在此我们假设在股市综合指数日收盘价变化过程中存在“双区制”特征，①本文第三节中的实证检验结论表明，此“双区制”对应着中国股市运行中的综合指数“高日收盘价”和“低日收盘价”两个阶段。模型中的所有参数都是状态相依的，并且都受制于St，双区制之间的转移概率满足一阶马尔科夫过程，将转移概率矩阵表示为如下的形式：

其中，pij具体代表区制状态变量Pr［St＝j｜St－1＝i］从St时刻的t－1状态转移变迁至t时刻的j状态的转移概率值，并且还满足条件：为了具体估计上述所构建的马尔科夫区制转移模型，我们在此考虑基于过去信息集It－1，πt，St以及St－1的联合分布密度：

根据方程（7）我们能够进一步计算边际分布：

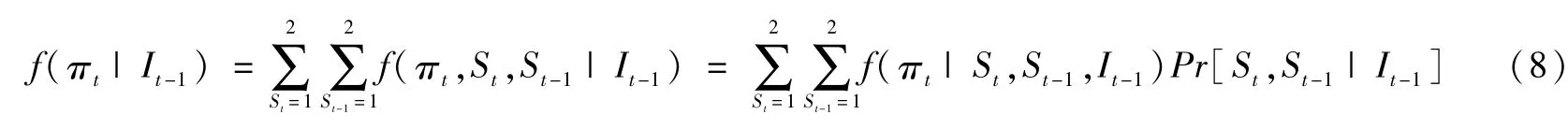
而由方程（8）我可以进一步计算对数似然函数：

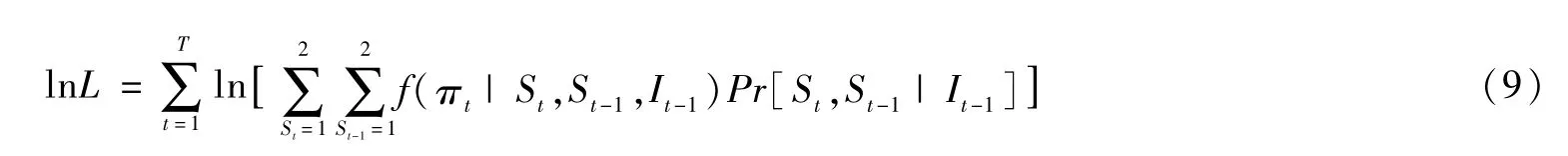
其中，Pr［St＝j，St－1＝i｜It－1］＝Pr［St＝j｜St－1＝i］Pr［St－1＝i｜It－1］，i，j＝1，2。利用所获得的加权项Pr［St，St－1｜It－1］更新方程（9），即：

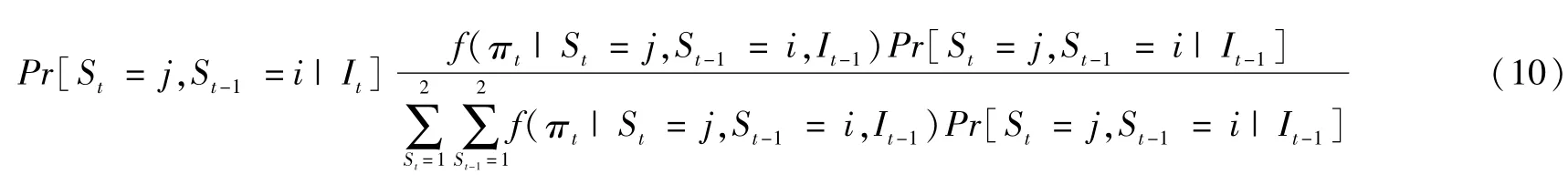
三、中国沪深股市牛熊市的动态路径区制状态划分

本文选取2002年1月4日至2014年3月31日期间中国上证综合指数日收盘价数据以及深证综合指数日收盘价数据进行实证研究。数据来源于锐思金融数据库，文中所涉及的所有程序由Gauss 9.0以及Eviews 5.0完成。图1、图2分别给出了中国上证综合指数和深证综合指数日收盘价序列的时间动态轨迹，其中横坐标代表年度时间，纵坐标代表股票价格指数。图中的趋势成分是运用H－P滤波得到的，序列中的波动成分，就是原序列扣除趋势成分的剩余部分，表征日收盘价的波动程度。

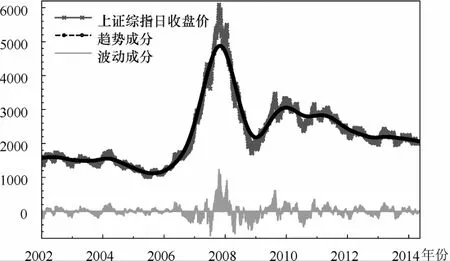
图1 上证综指日收盘价序列的时间动态轨迹

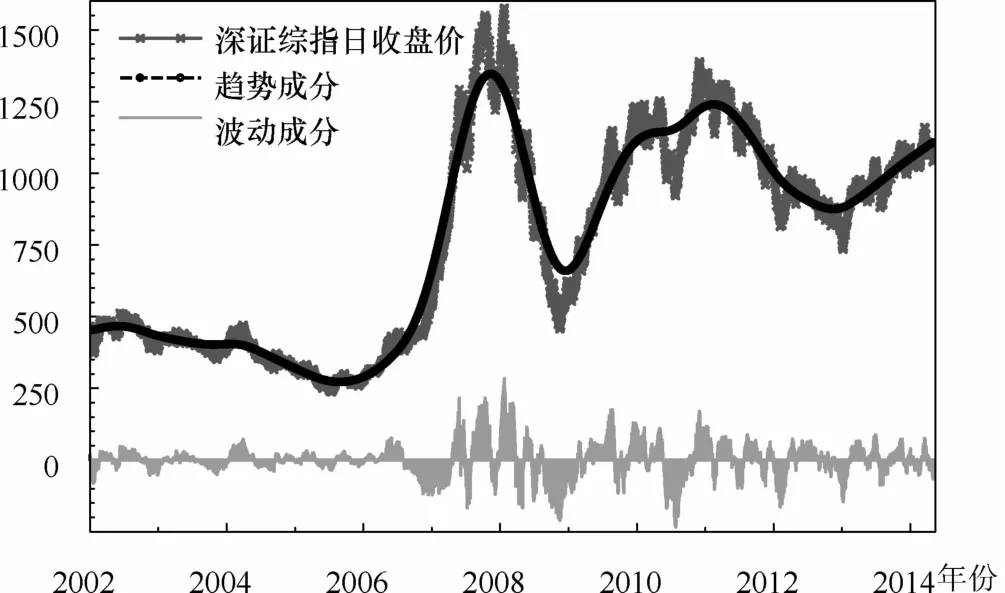
图2 深证综指日收盘价序列的时间动态轨迹

图1和图2分别给出了中国上证和深证综合指数日收盘价序列的时间变化轨迹。由图1和图2我们可以看出，沪深股市综合指数日收盘价时间序列总体上具有较为相似的动态变化路径，同时注意到，在2002年初至2005年末的期间内，两序列均呈现出相对平缓的发展态势，而在2006年初至2007年末的两年时间内，两序列却都体现出明显的持续攀升势头，但是从2008年至今，两序列同时表现出两轮显著的陡然下降态势。虽然图1和图2初步显示了中国沪深股市综合指数日收盘价的动态变化路径，但是从这两个图中我们尚无法准确刻画沪深股市综合指数日收盘价具体在何时、在何种条件下发生了结构性变化。

我们运用极大似然估计方法通过Gauss 9.0语言编程估计前文所述的马尔科夫区制转移模型，最终得到如表1所示的滞后1阶情形下模型参数、转移概率矩阵、对数似然值等的具体估计结果。可以看出，均值参数、自回归系数和方差在不同区制下的估计结果均十分显著，这表明本文所构建的马尔科夫区制转移模型能够十分合理而准确地刻画中国沪深股市综合指数日收盘价序列存在明显的“双区制”动态变化特征。此外，上证综合指数处于“低日收盘价”区制（St＝1）时的维持概率为p11＝0.9903，处于“高日收盘价”区制（St＝2）时的维持概率为p22＝0.9778；相对应地，处于“低日收盘价”区制时的平均持续期约为103天（D（St）＝（1－p11）－11＝1／（1－0.9903）＝103.0928），处于“高日收盘价”区制时的平均持续期约为45天（1／（1－0.9778））。深证综合指数处于“低日收盘价”区制（St＝1）时的维持概率为p11＝0.9964，处于“高日收盘价”区制（St＝2）时的维持概率为p22＝0.9976；相对应地，处于“低日收盘价”区制时的平均持续期约为278天（1／（1－0.9964）），处于“高日收盘价”区制时的平均持续期约为417天（1／（1－0.9976））。这意味着上证综合指数处于“低日收盘价”区制时的持续性显著强于其处于“高日收盘价”区制时的持续性，深证综合指数处于“低日收盘价”区制时的持续性显著弱于其处于“高日收盘价”区制时的持续性，与上证综合指数相比较，深证综合指数无论是步入“低日收盘价”区制抑或“高日收盘价”区制时的持续性都更强一些。另一方面，上证综合指数处于“低日收盘价”区制时的方差（σ＝0.0222）显著低于其处于“高日收盘价”区制时的方差（σ＝0.0805），同样，深证综合指数处于“低日收盘价”区制时的方差（σ＝0.0048）也明显低于其处于“高日收盘价”区制时的方差（σ2＝0.0215），这意味着在中国股票市场运行历程中，当股票价格持续走高时，通常会伴随着较大的波动性（此波动性又可称为不确定性）。

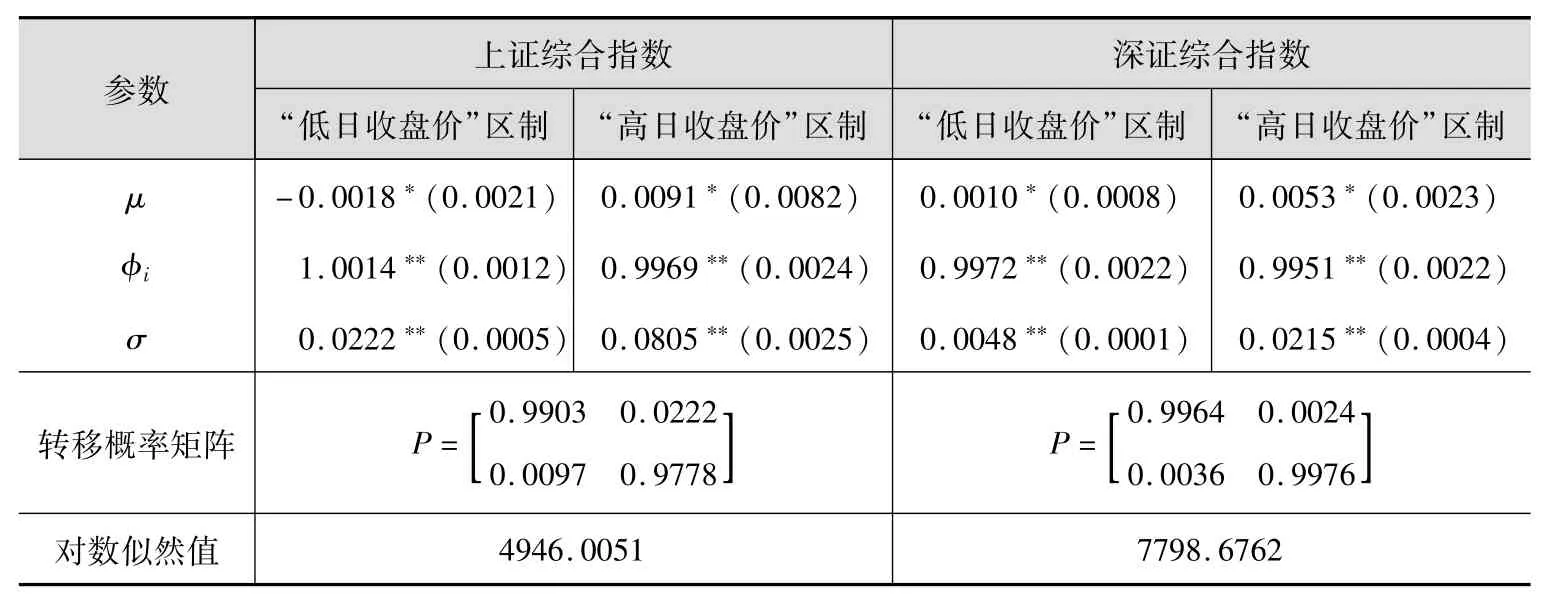
表1 滞后1阶的马尔科夫区制转移模型估计结果

由于平滑概率能够具体描述股市综合指数日收盘价在t＝1，2，…，T时所处区制状态发生转移的概率，在此我们基于马尔科夫区制转移模型进一步计算了区制状态变量St在所研究的总体样本区间内离散取值的平滑概率。图3、图4以及图5、图6分别清晰地刻画出中国沪深股市综合指数处于“低日收盘价”区制（St＝1）以及“高日收盘价”区制（St＝2）时的平滑概率。一般而言，当区制状态变量St的概率值Pr（St＝i｜It）＞0.5，i＝1，2时，区制转移发生，即此时处于i区制（i＝1，2）当中，概率值愈大，说明股市综合指数处于此区制的可能性也就愈大。

观察图3和图4发现，上证综合指数在2002年年初至2006年年末以及2011年年初至今的期间内处于“低日收盘价”区制（Pr（St＝1｜It）＞0.5）当中；而在2007年年初至2010年年末的时间内处于“高日收盘价”区制（Pr（St＝2｜It）＞0.5）当中。图5和图6说明，深证综合指数在2002年年初至2006年年末的期间内处于“低日收盘价”区制（Pr（St＝1｜It）＞0.5）当中；而在2007年年初至今的时间内处于“高日收盘价”区制（Pr（St＝2｜It）＞0.5）当中。

对样本区间内平滑概率值的时间变动轨迹进行综合比较发现，就上证综合指数而言，在2007年年初至今的时间范围内，表征日收盘价高低的平滑概率值呈现出剧烈的波动态势，而在2002年年初至2006年年末的时间范围内，上证综合指数处于“低日收盘价”区制的平滑概率值基本维持在1.0附近。就深证综合指数来讲，无论是在2002年年初至2006年年末期间处于“低日收盘价”区制时，还是在2007年年初至今期间处于“高日收盘价”区制时，其平滑概率值大致都维持在1.0左右。总之，需要强调的是，基于马尔科夫区制转移模型而得到的平滑概率值计算结果表明在中国金融市场变迁过程中，股市综合指数日收盘价序列在2006年年末或2007年年初发生了显著的结构性突变，即出现了在“低日收盘价”区制和“高日收盘价”区制间的相互变迁。

图3 上证综合指数“低日收盘价”区制（St＝1）

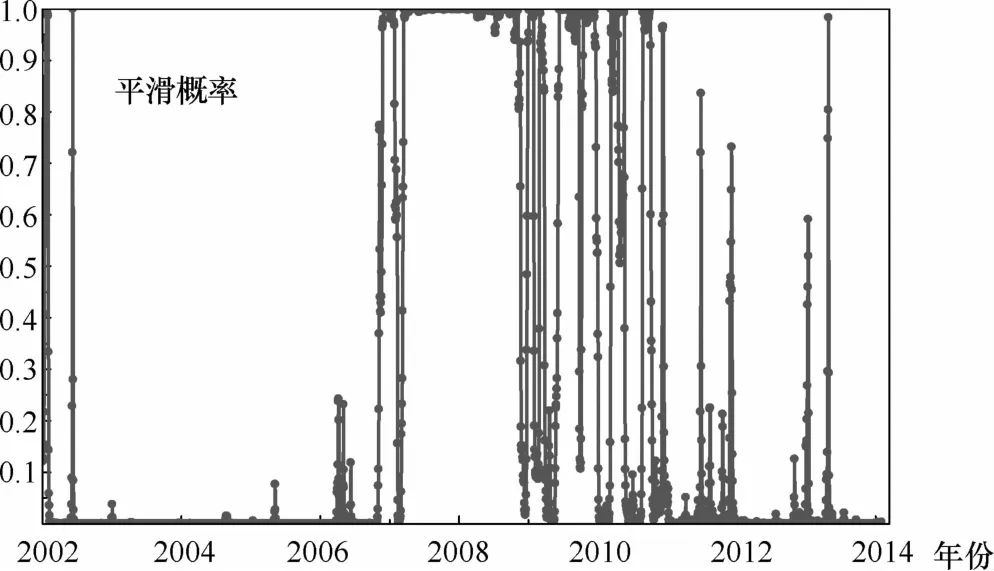
图4 上证综合指数“高日收盘价”区制（St＝2）

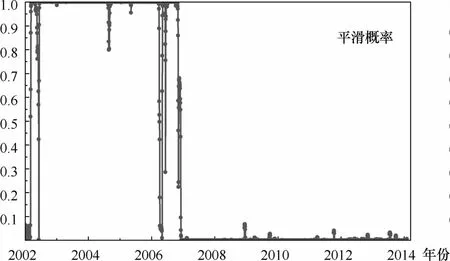
图5 深证综合指数“低日收盘价”区制（St＝1）

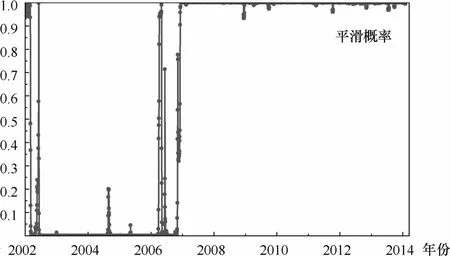
图6 深证综合指数“高日收盘价”区制（St＝2）

四、基本结论及政策启示

（一）本文所构建的马尔科夫区制转移模型能够十分合理而准确地刻画中国沪深股市综合指数日收盘价序列存在明显的“双区制”动态变化特征。此外，上证综合指数处于“低日收盘价”区制时的维持概率为p11＝0.9903，处于“高日收盘价”区制时的维持概率为p22＝0.9778；相对应地，处于“低日收盘价”区制时的平均持续期约为103天，处于“高日收盘价”区制时的平均持续期约为45天。深证综合指数处于“低日收盘价”区制时的维持概率为p11＝0.9964，处于“高日收盘价”区制时的维持概率为p22＝0.9976；相对应地，处于“低日收盘价”区制时的平均持续期约为278天，处于“高日收盘价”区制时的平均持续期约为417天。这意味着上证综合指数处于“低日收盘价”区制时的持续性显著强于其处于“高日收盘价”区制时的持续性，深证综合指数处于“低日收盘价”区制时的持续性显著弱于其处于“高日收盘价”区制时的持续性，与上证综合指数相比较，深证综合指数无论是步入“低日收盘价”区制抑或“高日收盘价”区制时的持续性都更强一些。

（二）上证综合指数处于“低日收盘价”区制时的方差显著低于其处于“高日收盘价”区制时的方差，同样，深证综合指数处于“低日收盘价”区制时的方差也明显低于其处于“高日收盘价”区制时的方差，这意味着在中国股票市场运行历程中，当股票价格持续走高时，通常会伴随着较大的波动性（此波动性又可称为不确定性）。

（三）上证综合指数在2002年年初至2006年年末以及2011年年初至今的期间内处于“低日收盘价”区制当中；而在2007年年初至2010年年末的时间内处于“高日收盘价”区制当中。深证综合指数在2002年年初至2006年年末的期间内处于“低日收盘价”区制当中；而在2007年年初至今的时间内处于“高日收盘价”区制当中。

（四）对样本区间内平滑概率值的时间变动轨迹进行综合比较发现，就上证综合指数而言，在2007年年初至今的时间范围内，表征日收盘价高低的平滑概率值呈现出剧烈的波动态势，而在2002年年初至2006年年末的时间范围内，上证综合指数处于“低日收盘价”区制的平滑概率值基本维持在1.0附近。就深证综合指数来讲，无论是在2002年年初至2006年年末期间处于“低日收盘价”区制时，还是2007年年初至今期间处于“高日收盘价”区制时，其平滑概率值大致都维持在1.0左右。由此，基于马尔科夫区制转移模型而得到的平滑概率值计算结果进一步印证了在中国金融市场变迁过程中，股市综合指数日收盘价序列在2006年年末或2007年年初确实发生了显著的结构性突变，即出现了在“低日收盘价”区制和“高日收盘价”区制间的相互变迁。

通过马尔科夫区制转移模型可以估计日收盘价序列数据生成过程中发生结构转变的转移概率，而且可以刻画出该时间序列的内生变化特征，因而可以更为深入地给出任意时刻某一日收盘价格所处的区制以及区制之间发生相互转移的确切时间。由该区制转移发生的确切时间能够分析并对比得到不同时域区间内的经济政策对股市周期的影响效果，并借此诊断出宏观经济调控政策对中国股市周期的划分作用。我们发现在本文研究的样本区间内，中国沪深股市综合指数日收盘价序列发生了在“低日收盘价”区制和“高日收盘价”区制间的转移，即出现了牛市和熊市周期的转换。研究结果更深刻的体现出中国股票市场作为经济“晴雨表”角色特征。此外，本文对中国股市牛熊市的划分也对相关研究具有基础性的意义。根据所判断的牛熊市态势，中国相关监管机构应审时度势，准确判断中国股市所处的区制状态及其波动性特征，并及时采取有效措施进行适时适度的宏观调控，以促进中国股票市场的健康、持续、稳健发展。

［1］Burns A F，Mitchel W C.Measuring Business Cycles［M］.New York：National Bureau of Economic Research，1946.

［2］Hodrick R J，Prescott E C.Postwar US Business Cycles：An Empirical Investigation［J］.Journal of Money，Credit and Banking，1997：1－16.

［3］Campbell J Y，Lo A W，A C，MacKinlay.The Econometrics of Financial Markets［M］.New Jersey：Princeton University Press，1997.

［4］Maheu J M，McCurdy T H.Identifying Bull and Bear Markets in Stock Returns［J］.Journal of Business＆Economic Statistics，2000，18（1）：100－112.

［5］Pagan A R，Sossounov K A.A Simple Framework for Analysing Bull and Bear Markets［J］.Journal of Applied Econometrics，2003，18（1）：23－46.

［6］Edwards S，Biscarri J G，Pérez de Gracia F.Stock Market Cycles，Financial Liberalization and Volatility［J］.Journal of International Money and Finance，2003，22（7）：925－955.

［7］Biscarri J G，De Gracia F P.Stock Market Cycles and Stock Market Development in Spain［J］.Spanish Economic Review，2004，6（2）：127－151.

［8］Gonzalez L，Powell J G，Shi J，et al.Two Centuries of Bull and Bear Market Cycles［J］.International Review of Economics＆Finance，2005，14（4）：469－486.

［9］孟卫东，严太华，杨杰.上证指数的星期效应研究［J］.经济问题，2000（1）：49－53.

［10］朱战宇，吴冲锋，王承炜.不同检验周期下中国股市价格动量的盈利性研究［J］.世界经济，2003，8（8）：62－67.

［11］黄继平，黄良文.中国股市波动的周期性研究［J］.统计研究，2003（11）：9－14.

［12］陆蓉，徐龙炳.“牛市”和“熊市”对信息的不平衡性反应研究［J］.经济研究，2004（3）：65－72.

［13］何兴强，周开国.牛熊市周期和股市间的周期协同性［J］.管理世界，2006（4）：35－40.

［14］夏南新.基于分形R／S技术的中国股市非规则周期性研究［J］.统计研究，2006（2）：28－31.

［15］周孝华，黄赟.中国股票市场沪深两市波动性关系研究［J］.经济与管理研究，2008（8）：77－82.

［16］郝梅瑞，周观君.中国股票市场新股长期价格行为研究［J］.经济与管理研究，2006（9）：53－59.

［17］祖垒，崔志伟，李自然.上证指数波动持久性在牛熊市的差异［J］.中国管理科学，2011，19（2）：57－62.

［18］Garcia R，Perron P.An Analysis of the Real Interest Rate Under Regimes Shifts［J］.The Review of Economics and Statistics，1996，35（4）：98－135.

［19］刘金全，郑挺国.利率期限结构的马尔科夫区制转移模型与实证分析［J］.经济研究，2006（11）：82－91.

［20］龙如银，郑挺国，云航.Markov区制转移模型与中国通货膨胀波动路径的动态特征［J］.数量经济技术经济研究，2005（10）：111－117.

［21］刘金全，隋建利，闫超.中国通货膨胀率过程区制状态划分与转移分析［J］.系统工程学报，2009，24（6）：647－652.

［22］刘金全，刘志刚.具有马尔科夫区制转移的向量误差修正模型及其应用［J］.管理科学学报，2006，9（5）：44－49.

［23］张小宇，刘金全.规则型货币政策与通货膨胀平稳性的内在关联机制研究［J］.经济与管理研究，2012（9）：25－32.

［24］李敏，王相宁，缪柏其.基于马尔科夫区制转移模型的人民币实际有效汇率波动机制［J］.中国科学技术大学学报，2010，40（6）：565－570.

［25］蒋祥林，李一凡.基于区制转移模型的中国短期利率动态行为实证研究［J］.世界经济情况，2011（4）：48－62.

［26］Hamilton J D.A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle［J］.Econometrica，1989，57（2）：357－384.

The Operation Cycles of Bull and Bear Stock Markets in China——Based on Markov Regime-switching Model

YAN Chao，LIU Jin-quan，SUI Jian-li
（School of Business and Quantitative Research Center of Economics，Jilin University，Changchun 130012）

This paper uses Markov regime-switching model to investigate the dynamic path of day’s closing price of composite index in the Chinese stock market，in order to analyze the operation cycles of the bull and bear markets in China.According to the empirical results，the time series of day’s closing price can be divided into‘low price’regime and‘high price’regime，and Shanghai and Shenzhen composite indexes in the different regimes are able to reflect the obvious sustaining characteristics.At the same time，there is obvious collaborative between Shanghai and Shenzhen composite indexes.Moreover，there is obvious correlation between China’s economic policy mechanisms and the different regimes of day’s closing price of composite index in China’s stock market.

Stock Market；Bull Market；Bear Market；Markov Regime-Switching Model；Smoothing Probabilities

F831

A

1000－7636（2014）10－0045－08

责任编辑：高立红

2014－07－21

国家社会科学基金重大项目“‘十二五’期间中国经济周期波动态势与宏观经济调控模式研究”（10ZD＆006）；中国博士后科学基金面上项目“中国城镇化进程中新生代农民工收入状况与消费行为研究”（2013M530961）；中国博士后科学基金特别资助项目“经济转轨期中国经济周期波动态势与宏观调控模式研究”（2014T70272）；吉林大学基本科研业务费项目“新形势下中国农民消费对经济增长的作用机制与传导机制研究”（2012BS051）

闫 超 吉林大学商学院／数量经济研究中心讲师，长春市，130012；

刘金全 吉林大学商学院教授、博士生导师，教育部长江学者特聘教授；

隋建利 吉林大学商学院副教授。