基于复矢量电流调节器的指定次谐波电流控制方法研究
2014-06-01游小杰郭希铮
钟 畅,游小杰,郭希铮
(北京交通大学电气工程学院,北京100044)
基于复矢量电流调节器的指定次谐波电流控制方法研究
钟 畅,游小杰,郭希铮
(北京交通大学电气工程学院,北京100044)
三相并联型有源电力滤波器可以补偿电力系统中非线性负载引起的谐波与无功电流,其补偿性能取决于电流调节器的控制精度与动态响应。本文采用复矢量分析法,提出一种复矢量PI调节器控制方法,该方法对系统参数变化的鲁棒性较好;针对数字控制系统的固有延时,在离散域下,采用电压指令相位延迟补偿方法,消除延时对系统稳定性的影响;通过增加虚拟电阻,提高控制器的抗干扰性能,提高谐波补偿精度。仿真结果验证了上述方法的有效性。
指定次谐波消除;延时补偿;复矢量电流调节器;虚拟电阻法
1 引言
实际应用中,对于采用混合型电力滤波器或APF容量大小受限的情况而言,仅要求APF补偿危害较大的特征次谐波[1-3]。同时,对于特定次谐波单独设计控制器,有利于系统稳定性的提高。上述几个因素促使指定次谐波消除有源电力滤波器(Selective Harmonic Active Power Filter,SH-APF)得到广泛应用。SH-APF的优点主要有[3]:①有效减小设计容量,降低成本;②针对各次谐波单独设计控制器,对电路参数及电流控制延时敏感性低,可增强系统鲁棒性;③可以减小APF与负载之间,由负载阻抗中容性或谐振成分引起的振荡与相互影响。
目前,已有关于SH-APF的大量研究。文献[4,5]采用多同步旋转坐标系下传统PI控制器作为电流调节器,通过状态反馈解耦的方法消除由同步旋转坐标变换所产生的dq轴耦合,但同时引入了电路参数,导致控制器的动态性能变差。文献[6,7]采用静止坐标系下的比例积分(Proportional-Resonant,PR)控制器,由于无需采用同步旋转坐标变换,因此不存在耦合问题。但是在控制器设计过程中,如果离散方法选择或参数设计不当,将引起谐振频率偏移或各次谐波间产生串扰等问题。此外PR控制器的参数设计过程与PI控制器相比,较为复杂。
对于数字控制器而言,存在固有的采样与计算延时,将造成系统的不稳定[8]。对于非对称PWM与对称PWM而言,该固有延时分别为Ts/2 与Ts(Ts为采样周期)。文献[9]提出了在控制器设计中进行延时补偿的方法,但同时也增加了电流调节器的复杂程度,并且需要占用大量计算资源。
本文首先针对SH-APF中数字控制器的固有延时问题,在离散域下采用复矢量分析方法,分析控制对象的数学模型、系统的开环传递函数以及零极点分布,提出电压指令相位延迟补偿方法以抵消该固有延时所产生的影响,提高系统稳定性。其次,对于传统电流调节器鲁棒性较差的问题,提出采用复矢量PI电流调节器以消除系统对电路参数的依赖性,增加系统鲁棒性。同时针对几种不同电流控制器,进行抗干扰性能的分析与比较,并利用增加虚拟电阻的方法提高系统抗干扰性能。最后,在仿真分析中采用非对称SVPWM方式,增大等效开关频率,并利用仿真工具验证采用复矢量电流调节器进行指定次谐波电流控制方法的补偿效果。
2 SH-APF数学模型与控制策略
2.1 离散域下的SH-APF复矢量数学模型
图1为采用LCL型滤波器的三相SH-APF的电路拓扑图。对于谐振频率点前的低频段,LCL滤波器可等效视作L型滤波器[10]。
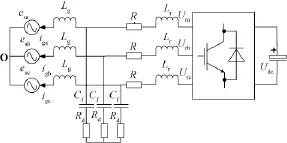
图1 三相SH-APF电路拓扑Fig.1 3-phase SH-APF topology
在静止复数坐标系下定义如下复变量形式:
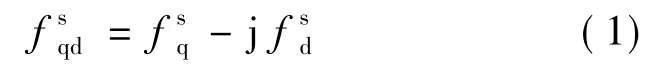
其中,上角标s,r分别表示该变量在静止或旋转坐标系下的值。由此可得,在静止坐标系下,SH-APF的复矢量框图(见图2),采用零阶保持器法对其进行离散化,即得系统的开环传递函数:
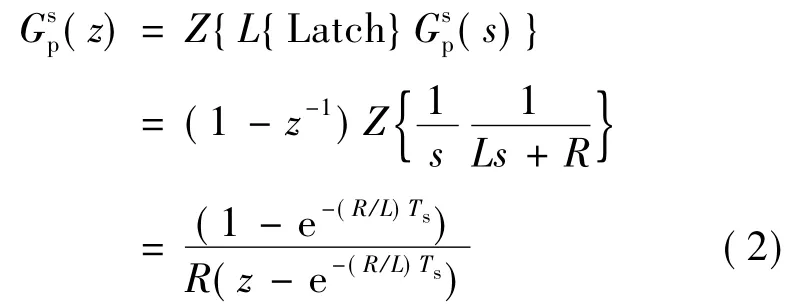

图2 三相SH-APF静止坐标系下的复矢量框图Fig.2 3-phase SH-APF complex vector state block diagram in stationary frame
经过旋转坐标变换,并考虑数字控制器存在的固有延时(同步旋转坐标系下,延时Ts表示为(z· ejωeTs)-1)之后,可得其在同步旋转坐标系下离散域开环传递函数:

2.2 SH-APF电流控制策略
指定次谐波检测通常有两种方式:一是采用检测网侧电流的方法[4],其优点在于仅需检测网侧电流,所需传感器数量较少;二是检测负载电流与APF发出电流的方法[5],优点在于可以为APF提供过电流保护。本文所用的SH-APF采用检测负载电流iLabc与APF电流iFabc的方法(见图3)。控制部分包含一个电压环,一个基波电流环以及一系列的谐波电流环。其中,采用传统PI控制器,目的是稳定SH-APF直流侧电压。基波及各次谐波电流环采用对应次旋转坐标系下的复矢量PI电流调节器进行控制,电流环指令通过提取iLabc与iFabc误差值在各次旋转坐标系下的直流分量得到。最后,将基波与各次谐波电流环输出的指令电压相叠加,经由SVPWM调制,即可控制SH-APF实现指定次谐波电流补偿。

图3 SH-APF指定次谐波电流控制策略框图Fig.3 SH-APF selective harmonic current control strategy block
3 离散域下电流调节器设计与分析
3.1 传统同步旋转坐标系下PI控制器
图4为离散域同步旋转坐标系下三相SH-APF复矢量框图,其中一阶低通滤波器与传统同步旋转坐标系下PI控制器的s域传递函数分别为:

采用Tustin变换(双线性插值法),对一阶滤波器及传统PI控制器离散化,可得:
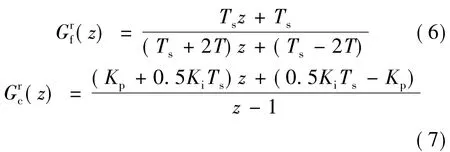

图4 采用同步旋转坐标系PI电流调节器的闭环系统离散域复矢量框图Fig.4 Complex vector state block of close loop system using discrete-time synchronous frame PI current regulator
通过式(8)可得系统闭环传递函数,并得到系统的闭环零极点分布(见图5)。
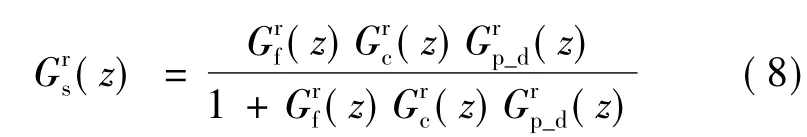

图5 同步旋转坐标系PI电流调节器的闭环系统零极点分布图(L=0.6mH,R=15mΩ,T=30ms,ωbw=2πkHz,fs=10kHz,fe:0~1kHz)Fig.5 Zero-pole migration of close loop system using synchronous frame PI current regulator (L=0.6mH,R=15mΩ,T=30ms,ωbw=2πkHz,fs=10kHz,fe:0~1kHz)
其中,实线标注的轨迹为系统中未加入一阶滤波器时的系统闭环零极点分布(A~B,C~D,E~F),虚线标注的为系统中加入一阶滤波器后的系统闭环零极点分布(A'~B',C'~D',E'~F',G'~H')。可见系统在一定条件下(fe/fs>0.07),闭环极点E~F,E'~F'在单位圆外,闭环系统不稳定。
3.2 数字控制器的延时补偿
数字控制器中所存在的固有延时是造成系统闭环极点随着fe/fs增大而逐渐不稳定的主要原因,需要在电流调节器设计中加以补偿。如式(9),通过提前电压指令的相位的方法(乘以ejωeTs项)来补偿数字控制器延时(见图6)[11],得到电流调节器传递函数如下:
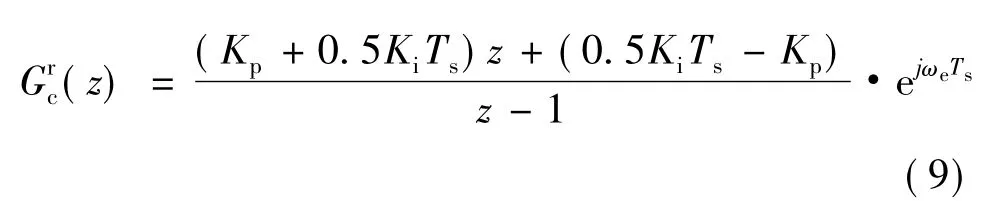
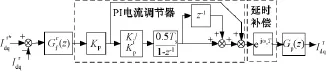
图6 采用考虑延时补偿的同步旋转坐标系PI电流调节器的闭环系统离散域复矢量框图Fig.6 Complex vector state block of close loop system using discrete-time synchronous frame PI current regulator with delay compensation
由式(8)可以得到系统闭环零极点分布,如图7所示。可见考虑了延时补偿之后,系统闭环极点E ~F,E'~F'均分布在单位圆内,系统稳定性得到改善。同时,由于加入一阶滤波器,系统闭环极点C~D移动至C'~D',当fe/fs>0.09时,闭环极点分布在单位圆外,因此在选取一阶滤波器的时间常数时,应该注意不宜取值过大,以免影响系统稳定性。
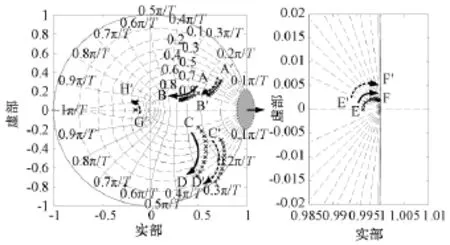
图7 考虑延时补偿的同步旋转坐标系PI电流调节器的闭环系统零极点分布图(L=0.6mH,R=15mΩ,T=30ms,ωbw=2πkHz,fs=10kHz,fe:0~1kHz)Fig.7 Zero-pole migration of close loop system using synchronous frame PI current regulator with delay compensation(L=0.6mH,R=15mΩ,T=30ms,ωbw=2πkHz,fs=10kHz,fe:0~1kHz)
由于控制对象经过旋转坐标变换至同步旋转坐标系下后,会产生dq轴间的相互耦合,如图8所示,将极大影响电流调节器的动态性能。
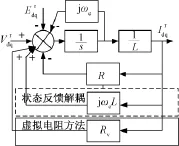
图8 三相APF在旋转坐标系下的复矢量框图Fig.8 Complex vector state block of 3-phase APF in synchronous frame
分析采用传统同步旋转坐标系下PI电流调节器的开环系统频域响应。如图9所示,可见虽然频率响应曲线在其同步旋转频率处增益为1,相角滞后为0°,但随着同步频率增大,系统的频域响应变化极大,可见系统的动态性能较差。

图9 采用考虑延时补偿的同步旋转坐标系PI电流调节器的开环系统频域响应(fe=0,50,200Hz)Fig.9 Frequency response of open loop system using synchronous frame PI current regulator with delay compensation(fe=0,50,200Hz)
3.3 复矢量电流调节器
为解决上述问题,本文采用如图10所示的一种修改电流控制器结构的方法,来实现相同解耦效果,即复矢量电流调节器[11]。对比于图8虚线框内的状态反馈解耦方法,复矢量电流调节器没有引入电路参数L,从而不会导致系统的动态控制性能以及对电路参数鲁棒性变差。其z域传递函数如下:
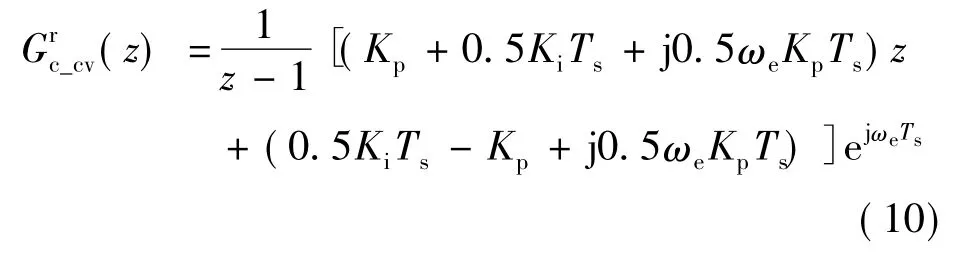
图11为采用复矢量PI电流调节器时,系统的频率响应。由图11(a)可见采用复矢量的PI电流调节器后,频率响应变得相对平滑,且在同步旋转频率附近增益近似为1,由图11(b)可见,无论L取值如何,开环系统的频率响应一致,因此可见由电路参数估计误差产生的影响也相应被消除了。
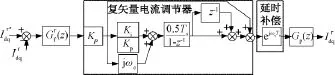
图10 采用考虑延时补偿的复矢量PI电流调节器的闭环系统离散域复矢量框图Fig.10 Discrete-time complex vector state block of close loop system using complex vector PI current regulator with delay compensation

图11 采用复矢量PI电流调节器的开环系统频域响应Fig.11 Frequency response of open loop system using complex vector PI current regulator
3.4 抗干扰性分析
为分析抗干扰性,引入抗扰强度函数,其物理意义是:产生单位的受扰输出需要作用的外部干扰强度。因此,抗干扰强度函数的数值越大,系统对干扰信号的鲁棒性越好,抗干扰能力就越强。

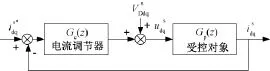
图12 静止旋转坐标系下考虑电压干扰作用时系统框图Fig.12 System state block with disturbance voltage in stationary frame
为了提高系统的抗干扰强度,本文采用虚拟电阻的方法[12],如图8实线框中所示。
图13为前述几种电流调节器的抗干扰函数频率响应图,其中复矢量控制方法,在同步频率附近抗干扰性能较好,且随着同步旋转频率上升,复矢量PI电流调节器的抗干扰函数的最小值远小于其他几种电流调节器。另外,由图13中曲线(d)可见,采用虚拟电阻方法可以提高系统抗扰动函数的带宽,从而增加系统的抗干扰强度。
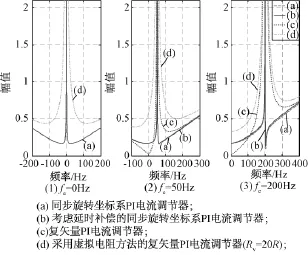
图13 静止坐标系下电流调节器抗干扰分析Fig.13 Analysis of dynamic stiffness of current regulators in stationary frame
4 仿真结果
为了进一步验证所提出SH-APF控制算法的有效性,采用Matlab/Simulink对前述内容进行仿真。仿真所采用的参数如表1所示,其中LCL滤波器的参数按照文献[13]中所提出的设计方法进行设计。
负载谐波电流波形及其频谱如图14(a)和14 (c)所示。如图14(b)和图14(d)所示,经过SHAPF对5次谐波补偿后,该次谐波的谐波畸变率大大降低,由未补偿之前的22.62%下降至0.44%。

表1SH-APF系统参数Tab.1 SH-APF system parameters
图15(a)、15(c)与15(b)、15(d)分别为SHAPF采用复矢量电流调节器与传统PI电流调节器补偿5、7、11、13、17、19次谐波时电网侧电流波形及其频谱。表2为补偿前后各次谐波电流的畸变率。对比二者的补偿效果可见,相比于传统PI电流调节器而言,采用复矢量电流调节器的SH-APF对指定次谐波的抑制效果略好于前者,系统的总谐波畸变率从补偿前的30.04%下降至补偿后的10.49%,前者为11.30%。

表2SH-APF补偿前后谐波电流THDTab.2 THD of harmonic current before and after compensation by SH-APF
图16(a)和16(b)为分别采用复矢量电流调节器和传统PI电流调节器,负载由14.44kVA切换至28.88kVA时网侧A相电流波形。可见,当采用复矢量电流调节器时,网侧电流经过1~2个周期过渡过程后达到稳定,且过渡过程较平滑;当采用传统PI电流调节器时,网侧电流经过3~4个周期过渡过程后达到稳定,过渡过程较平滑,过渡过程畸变较大。由此可知,所采用的复矢量电流调节器动态性能较好。
图17为网侧电压突增10%时,网侧的A相电压与A相电流波形。其中,图17(a)未采用虚拟电阻法,当网侧电压突变时,网侧电流出现较大畸变,需要2~3个周期过渡过程才能达到稳态;图17(b)采用虚拟电阻法(Rv=20R),网侧电压突变时,网侧电流畸变较小,且在1~2个过渡周期后即达到稳态。仿真结果验证了采用虚拟电阻法可以有效地增加系统的抗干扰强度。
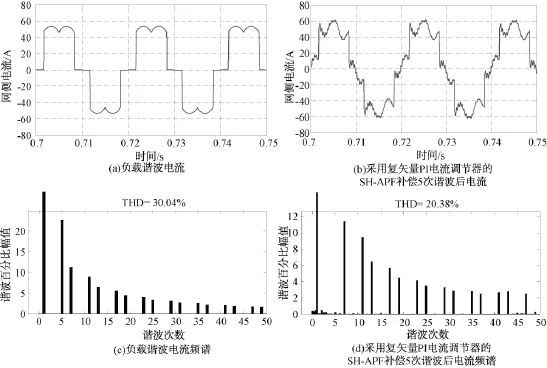
图14负载电流波形及其频谱与仅补偿5次谐波电流后网侧电流波形及其频谱Fig.14 Load current waveform and its magnitude spectrum and waveforms and magnitude spectrum of grid side current with only fifth harmonic compensated

图15 补偿5、7、11、13、17、19次谐波电流后网侧电流波形及其频谱Fig.15 Waveforms and magnitude spectrum of grid side current with5th,7th,11th,13th,17thand 19thharmonic compensation
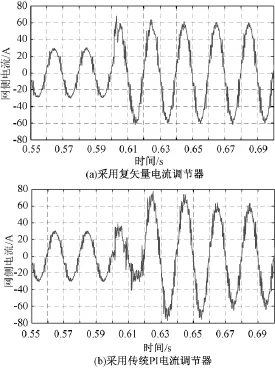
图16 投切负载时网侧电流波形Fig.16 Dynamic grid-side current waveforms with load switch

图17 网侧电压突变10%时网侧电压电流波形Fig.17 Dynamic grid-side voltage and current waveforms with 10%sudden increase of grid-side voltage
5 结论
本文提出基于复矢量PI电流调节器的SHAPF,通过理论分析与仿真表明:
(1)通过提前指令电压相位的方法,可以有效补偿数字控制器的固有延时,提高系统稳定性;
(2)采用复矢量PI电流调节器,可以减小对系统参数的敏感性,提高系统鲁棒性;
(3)增加虚拟电阻的方法,可以有效减小电流脉动,增大电流控制精度与抗干扰性;
(4)所提出的SH-APF控制策略,有极好的指定次谐波电流补偿精度,达到良好的补偿效果。
[1]王兆安,杨君,刘进军 (Wang Zhaoan,Yang Jun,Liu Jinjun).谐波抑制和无功功率补偿 (Harmonic reduction and compensation for reactive power) [M].北京:机械工业出版社 (Beijing:China Machine Press),1998.245-310.
[2]J K Chatterjee,Shankar Subramanian,Dhiraj Bharat.Performance improvement in selective harmonic compensation of shunt hybrid active filter[A].2011 International Conference on Power and Energy System(ICPS) [C].Chennai,India,2011.1-6.
[3]Mattavelli P,Marafo F P.Repetitive-based control for selective harmonic compensation in active power filters [J].IEEE Transactions on Industrial Electronics,2004,51(5):722-729.
[4]Mattavelli P,Fasolo S.A closed-loop selective harmonic compensation for active filters[A].IEEE APEC 2000 [C].Louisiana,USA,2000.81-89.
[5]张树全,戴珂,谢斌,等 (Zhang Shuquan,Dai Ke,Xie Bin,et al.).多同步旋转坐标系下指定次谐波电流控制 (Selective harmonic current control based on multiple synchronous rotating coordinates)[J].中国电机工程学报 (Proceedings of the CSEE),2010,30 (3):55-62.
[6]Wanchak Lenwari.Optimized design of modified proportional-resonant controller for current control of active filters[A].2013 IEEE International Conference on Industrial Technology(ICIT)[C].Cape Town,South Africa,2013.894-899.
[7]Lenwari W,Sumner M,Zanchetta P,et al.A high performance harmonic current control for shunt active filters based on resonant compensators[A].IECON 2006-
(,cont.on p.57)(,cont.from p.29)32nd Annual Conference on IEEE Industrial Electronics [C].Paris,France,2006.2109-2114.
[8]李红雨,吴隆辉,卓放,等 (Li Hongyu,Wu Longhui,Zhuo Fang,et al.).有源电力滤波器补偿延时及对策的研究 (Study on compensation delay and its countermeasure of active power filter) [J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2005,24(3):18-21.
[9]范瑞祥,罗安,唐杰 (Fan Ruixiang,Luo An,Tang Jie).谐振注入式有源滤波器数字化控制系统延时研究 (The research of the delay based on digital control system of resonance injection active power filter) [J].中国电机工程学报 (Proceedings of the CSEE),2007,27(13):104-110.
[10]Fainan A Magueed,Jan Svensson.Control of VSC connected to the grid through LCL-filter to achieve balanced currents[A].Fourtieth IAS Annual Meeting[C].2005.572-578.
[11]Hongrae Kim,Michael Degner,Juan M Guerrero,et al.Discrete-time current regulator design for AC machine drives[A].ECCE 2009[C].San Jose,CA,USA,2009.1317-1324.
[12]郭希铮,游小杰,王晓丹 (Guo Xizheng,You Xiaojie,Wang Xiaodan).永磁同步电机电流调节器动态特性改进方法分析 (Dynamic characteristics improvement of current regulator for permanent magnet synchronous motor)[J].电力自动化设备(Electric Power Automation Equipment),2011,31(6):39-44.
[13]李欣然,郭希铮,王德伟,等 (Li Xinran,Guo Xizheng,Wang Dewei,et al.).基于LCL滤波的大功率三相电压型PWM整流器(Research and development of high-power three-phase voltage source PWM rectifier with LCL filter) [J].电工技术学报 (Transactions of China Electrotechnical Society),2011,26(8):79-84.
Selective-harmonic active power filter using complex vector PI current regulator
ZHONG Chang,YOU Xiao-jie,GUO Xi-zheng
(School of Electrical Engineering,Beijing Jiaotong University,Beijing 100044,China)
Three-phase Shunt Active Power Filter(SAPF)is a power electronic device compensating the harmonics and inactive power produced by non-linear load in the power system.And its compensation performance is primarily decided by the control accuracy and dynamics of the current regulator.In this paper,a complex vector PI current regulator is introduced which has decent robustness for system parameters.In order to eliminate influences of the intrinsic delay in the digital control system on the stability,a method for compensating the delay by advancing the phase of voltage command is employed.Additionally,the virtual resistance method is proposed for the sake of enhancing the stiffness of system and improving the accuracy of selective harmonic compensation.Finally,simulation tool is used to validate the proposed method.
SH-APF;delay compensation;complex current regulator;virtual resistance method
TM46
A
1003-3076(2014)06-0023-07
2013-09-16
国家电网公司科技项目资助(合同号:DL71-10-001)
钟 畅(1990-),男(畲族),福建籍,硕士研究生,研究方向为电力电子变流装置以及永磁同步电机控制;游小杰(1964-),男,福建籍,教授,博士,研究方向为电力电子技术在电力系统中的应用、变频调速技术等。
