特高压输电线路无源干扰谐振特性及其影响因子研究

唐 波，张建功，王惠丽，葛光祖，刘兴发

(1．三峡大学电气与新能源学院，湖北宜昌443002;2．中国电力科学研究院，湖北武汉430074; 3．河南省电力公司三门峡供电公司，河南三门峡210098)

特高压输电线路无源干扰谐振特性及其影响因子研究

唐 波1，张建功2，王惠丽3，葛光祖1，刘兴发2

(1．三峡大学电气与新能源学院，湖北宜昌443002;2．中国电力科学研究院，湖北武汉430074; 3．河南省电力公司三门峡供电公司，河南三门峡210098)

特高压输电线路对各类无线电台站的无源干扰存在着谐振的现象。IEEE仅给出了535～1705kHz范围内，输电线路无源干扰的谐振机理和谐振频率。为研究更高频率下的无源干扰谐振特性，采用特高压输电线路无源干扰线-面混合模型进行仿真分析，即铁塔采用面模型，地线采用线模型，整个模型由垂直极化平面波进行激励。基于矩量法，对线-面模型接点处的基函数及求解方法进行了介绍，并求解了0.5～50.5MHz范围内不同频率下的无源干扰水平。对有可能影响无源干扰谐振特性的因子，如地线、导线、铁塔数量及线路档距进行了研究。分析结果表明，线路档距是影响无源干扰谐振的决定性因子。

特高压输电线路;无源干扰;谐振特性;线-面模型;矩量法;影响因子

1 引言

随着我国特高压电网的建设，特高压输电线路对周边各类无线台站无源干扰防护间距的确定是亟需解决的问题［1，2］。然而，由于无线台站种类繁多，允许的干扰水平也不一致，加上特高压线路所经地区的地形地貌复杂，目前很难用实验的方法确定线路对无线台站的防护间距［3］。

IEEE在1996年给出了关于中波广播台的二次辐射计算导则［4］，建议具体的无源干扰问题可根据实际台站和线路的布局建立广播天线和铁塔线模型，通过数学计算的方法预测其谐振频率，即干扰最大值出现的频率。谐振频率根据铁塔和地线是否组成回路进行判定:当铁塔与地线相连时，两基铁塔及其之间的地线与它们对大地的镜像所组成的回路长度达整数倍波长时产生谐振(以下称“整数倍波长回路谐振频率”);当铁塔与地线绝缘时，铁塔高度为1/4波长时产生谐振(以下称“λ/4谐振频率”)。由于该标准是1996年针对中波广播电台而言提出的适用频率仅为535～1705kHz。

随着我国输电线路的电压等级逐步提高，特高压线路对无线台站的无源干扰日趋严重，为保证无线台站的正常工作，需提出防护间距的国家标准作为特高压线路路径选择设计时的参考。文献［2，5，6］中，提出了特高压输电线路无源干扰的线模型和特高压交流线路对各类无线台站的防护间距标准建议。

文献［2，5，6］说明了输电线路无源干扰线模型的等效依据及其求解方法，但认为频率超过16.7MHz以后，线模型由于误差过大将失效。文献［7］分析了采用线模型计算时偏差随频率增加而变大的原因，并提出了适用于更高频率的特高压输电线路无源干扰线－面混合模型。文献［8］进一步研究认为，无源干扰的谐振频率是防护间距计算的关键，而且当频率达短波频段及以上，传统上的“整数倍波长回路谐振频率”不再适用。

本文利用线-面模型对特高压输电线路无源干扰的谐振特性进行研究，考虑了多种对谐振频率产生影响的因子，如地线、导线、铁塔数量、线路档距等。分析结果表明，特高压线路的无源干扰主要在短波及以上频段，由铁塔产生的电磁散射引起，其谐振频率主要和线路档距相关。

2 特高压无源干扰的计算方法

由于各类无线台站天线的种类、大小和型号均不同，很难用确切的无线台站天线对输电线路仿真模型进行激励。因此，只能假设各类无线台站在无穷远处入射平面电磁波对输电线路模型进行激励。由于线路铁塔垂直于地面，因此考虑最严重的情况，即用垂直极化平面波为激励源，求解观测点处的电场变化，找出合适的距离保证电场变化在允许值以下，输电线路无源干扰可简化为如图1所示的数学模型。

图1 输电线路无源干扰的数学模型Fig．1 Mathematical model of reradiation interference from power transmission line

图1中有两个坐标系，一个是直角坐标系(x，y，z)，另一个是球坐标系(r，θ，φ)。设输电线路的铁塔、导线和地线为理想导体V，位于坐标轴x上，电磁波Ei以角度(θi，φi)入射到输电线路上，而输电线路上任一点r'处，即源点处感应电流密度分布为J(r')，向空间再辐射。设感应电流产生的散射电场为Es(r，θ，φ)，无线台站位于场点r。

在文献［7］中，根据输电线路的体、面和线仿真模型，得到了对应的输电线路无源干扰的体、面和线电场积分方程。根据矩量法，对相应的电场积分方程求解，可以得到图1中场点r处的电场矢量。

对发射天线或接收天线的无源干扰水平用分贝表示，即定义为:

式中，E有输电线路表示考虑线路影响后观测点的空间电场强度;E无输电线路表示无线路时观测点的空间电场强度。仿真计算时，取入射波的电场强度为1V/ m。

3 无源干扰线-面模型及其计算方法

3.1 模型的选择

从理论上看，仿真模型越近似于真实情况，计算得到的结果越准确。但对于输电线路这种复杂而且巨大的空间构筑物来说，随着激励电磁波频率的增加，按线路实际结构建模将带来无法接受的矩阵运算。因此，根据不同的激励频率，在输电线路仿真建模时可进行一定的简化处理。

以特高压直流输电线路为例，线路档距一般为500m，地线直径为厘米级，则可考虑地线仍用线模型代替。如±800kV向家坝-上海特高压直流线路采用 LBGJ-180-20AC型地线，该型地线直径为17.5mm。根据文献［9］的研究，采用线模型计算时，分段长度和半径之比不小于8，可计算得到分段长度不小于0.07m。若根据NEC计算要求，对模型按照 0.1倍波长划分，则该型地线可用于428.57MHz以下的计算。因此，对中短波频段的无线台站来说，输电线路模型可采用铁塔三维面模型和地线线模型的线－面混合结构。

特高压直流输电线路无源干扰模型如图2所示。以线路典型ZP30101型铁塔为对象进行仿真建模，该型铁塔高63m，横担长42.2m，两根地线相距32.4m，弧垂13m，档距长500m。

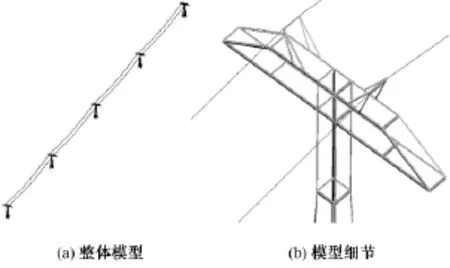
图2 特高压直流输电线路无源干扰模型Fig．2 Simulation model of reradiation interference from UHVDC

3.2 线-面混合模型的求解

对输电线路无源干扰的求解采用矩量法计算模型对应的电场积分方程。求解中，按照激励电磁波波长的一定比例对模型分段，选取分段单元对应的基函数和检验函数。对于线模型求解，选取脉冲基函数为基函数，检验函数选择Diracδ函数;对于面模型求解，基函数选择RWG基函数，采用伽略金检验。因此，采用线-面混合模型时，必然存在线-面结合点处的处理问题。

实际情况下的地线和铁塔通过金属地线线夹和铁塔相连，因此铁塔和地线上的感应电流应该是连续的，但若将面模型剖分为三角面元，细线模型剖分为线单元，则线单元和三角面元的交叉点处电流从物理意义上说具有不连续性。文献［10，11］对线-面连接处的处理进行了研究，提出线-面连接点基函数的具体表达可分为线部分和连接点周围的面部分。如图3所示，连接点j处的基函数可表示为［11］

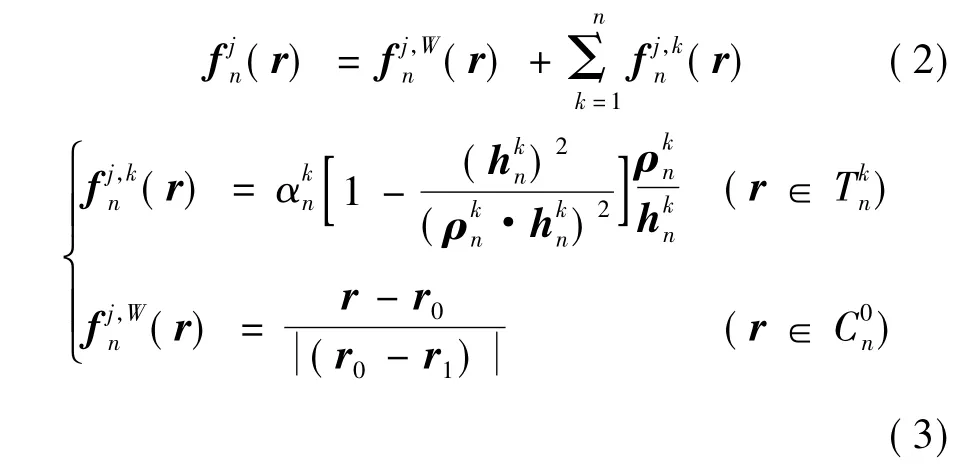
图3 线-面模型连接点处的基函数Fig．3 Base function at junction point in tower and ground wire

按照文献［7］的计算方法，将三种不同的基函数代入电场积分方程，并遵循矩量法的求解步骤，可得到矩阵方程，最终求解得到观测点的无源干扰值。

4 输电线路无源干扰谐振频率研究

4.1 地线对谐振频率的影响

文献［4］认为，地线和铁塔的连接决定了无源干扰谐振频率，对于没有地线的输电线路，铁塔被视为垂直天线，其最大干扰值发生在“λ/4谐振频率”;当铁塔和地线相连时，输电线路无源干扰谐振频率由铁塔、地线及其镜像组成的回路确定，当回路长度达整数倍波长时将产生谐振现象，其谐振频率由“整数倍波长回路谐振频率”决定。需要说明的是，该结论适合的频率范围为535～1705kHz。

文献［8］研究了地线对谐振频率的影响，结果表明，在短波频段地线的存在对无源干扰谐振特性没有影响，而在中波波段对谐振频率影响较大，能够较好地和文献［4］的研究一致，即符合“整数倍波长回路谐振频率”。但在整个中短波频段下，无源干扰水平随着频率增加出现了振荡的现象，而其极大值不符合“整数倍波长回路谐振频率”。

4.2 导线对谐振频率的影响

±800kV向家坝-上海特高压直流输电线路采用6×ACSR-720/50钢芯铝绞线，导线外径为36.24mm，分裂间隔距离为450mm。若按照标准［12］的计算方法，对分裂导线用等效单根导线半径Ri代入，其计算式为:

式中，R为分裂导线半径，即R=0.45m;n为次导线根数，n=6;r为次导线半径，r=0.01812mm。计算得到等效半径Ri为0.3551m。

为研究导线的分裂和弧垂对输电线路无源干扰的影响，建立5基铁塔和各种导线仿真模型。共有三种导线模型:没有弧垂的等效导线、有弧垂的等效导线和有弧垂的实际分裂导线。令入射电磁波以φ =180°入射，即垂直穿过铁塔阵列研究点P(2000，0，2)处的无源干扰强度，以1MHz为间隔，计算0.2 ～50.2MHz的输电线路无源干扰水平，计算结果如图4所示。

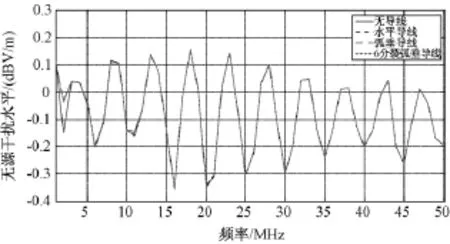
图4 导线对输电线路无源干扰的影响(防护间距2000m)Fig．4 Impact on interference from various conductors

从图4可以看出，4种模型的无源干扰数据曲线基本重合。对于0.2～50.2MHz的频段来说，导线的存在只是使输电无源干扰水平产生微量的偏差，但不影响无源干扰的谐振频率。同时，导线是否存在弧垂，对考虑分裂导线和不考虑分裂导线的结果也基本相同。这是由于模型采用垂直极化平面波激励，平行于地线的导线与平面波极化方向正交，导线对无源干扰基本上无影响。该计算结果与IEEE相关研究和实验结论一致。

4.3 铁塔数量对谐振频率的影响

目前特高压输电线路无源干扰研究中，均用5基铁塔来代替整条线路，且档距均为500m。为研究铁塔数量对谐振频率的影响，分别计算3基、5基和7基铁塔组成的输电线路的无源干扰水平。三种计算中，均保持中间铁塔位于坐标原点。取激励电磁波频段为0.2～50.2MHz，频率间隔1MHz，入射角度φ=180°，计算P(2000，0，2)点处的无源干扰水平，计算结果如图5所示。

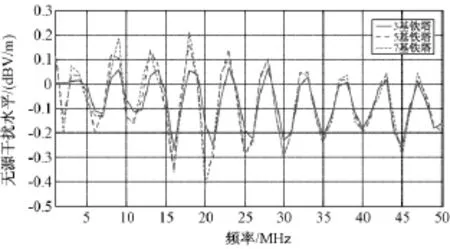
图5 铁塔数目对输电线路无源干扰的影响Fig．5 Impact on interference from number of towers

从图5中可以看出，铁塔数量基本上不影响无源干扰水平的振荡特性，而且在某数量铁塔无源干扰极值出现的频率点，其他数量铁塔的无源干扰也会出现极值。铁塔数量只影响无源干扰的极值大小及干扰最大值出现的频率，但不影响极值出现的频率。这说明，输电线路无源干扰谐振频率和铁塔数量关系很小。

另外需要注意的是，当铁塔数量为5基铁塔时，计算得到的无源干扰水平最大。这说明在5基铁塔两端各增加1基铁塔，反而还削弱了电磁散射干扰的强度，具体原因可能与电磁波的折反射有关，该问题还需要进一步研究。考虑到特高压直流输电线路档距为500m，5基铁塔所代表的输电线路长度已达2000m，在现实输电线路路径中，完全呈直线的输电线路长2000m以上的情况也不多，因此，特高压输电线路无源干扰模型采用5基铁塔对整条输电线路进行仿真是可行的。

4.4 档距对谐振频率的影响

为研究档距的变化对谐振频率的影响，设定不同的档距长度进行计算。档距分别取300m、500m 和700m，建立5基铁塔输电线路无源干扰模型。取激励电磁波频段为 0.5～50.5MHz，频率间隔1MHz，入射角度φ=180°，计算P(2000，0，2)点处的无源干扰水平，计算结果如图6所示。

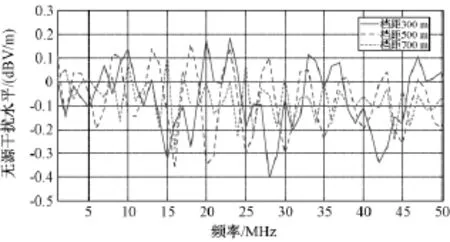
图6 档距大小对输电线路无源干扰的影响(防护间距2000m)Fig．6 Impact on interference from various spans

从图6中可以看出，档距300m时，无源干扰最大值为－0.4583dB，对应的频率为27.2MHz;档距500m时，无源干扰最大值为－0.3825dB，对应的频率为24.2MHz;档距700m时，无源干扰最大值为－0.3215dB，对应的频率为25.2MHz。结合图6中的无源干扰振荡曲线，可以认为档距是对输电线路无源干扰极值频率的决定影响因素，但很难发现其振荡规律。从整个0.2～50.2MHz频段看，5基铁塔无源干扰最大值随着档距的增加而减小。这从电磁散射的角度可以进行解释，整条输电线路对入射平面波的干扰包括了每基铁塔本身对激励电磁波的干扰以及铁塔之间相互的干扰。当档距越大，即铁塔相互间距越大，铁塔之间的相互电磁散射将逐步减小，从而导致整条线路无源干扰水平的下降。

5 结论

由上述研究可知，导线的存在对输电线路无源干扰水平及谐振频率基本没有影响，这也符合IEEE的相关研究和结论。地线的存在主要在中波频段对无源干扰谐振产生影响，可以认为输电线路无源干扰谐振由铁塔地线及其镜像组成的回路确定，即当回路达到整数倍波长时，回路中感应电流将达到最大值，从而造成输电线路二次辐射达到最大，直接影响到无源干扰特性。

在短波频段，输电线路无源干扰根本原因在于一定空间内无线电波受到输电线路金属部分的影响，档距是影响无源干扰谐振频率的决定性因素。因此，为减少输电线路对无线台站的无源干扰，可从宏观上尽量减少输电部分金属总量着手，如采用新型绝缘材料杆塔或者是扩大线路档距等方法。另外，从上述研究中可以看出，输电线路无源干扰水平随频率的增加其实是一个反复振荡的过程，必然存在一定的规律，这还需要继续深入研究。

［1］刘振亚 (Liu Zhenya)．特高压电网 (Ultra-high voltage grid)［M］．北京:中国经济出版社 (Beijing:China Economy Press)，2006．

［2］邬雄，万保权，张小武，等 (Wu Xiong，Wan Baoquan，Zhang Xiaowu，et al．)．1000kV特高压交流同塔双回线路对无线电台站影响及防护研究 (Reradiation interference and protection on radio station from 1000kV double-circuit power transmission line)［R］．武汉:国网武汉高压研究院 (Wuhan:Wuhan High Voltage Research Institute of SGCC)，2008．

［3］Toyada S，Hashimoto H．Scattering characteristics of VHF television broadcasting waves by steel towers of overhead power transmission lines［J］．IEEE Transactions on Electromagnetic Compatibility，1979，21(1):62-65．

［4］IEEE．IEEE Standard 1260-1996 IEEE guide on the prediction，measurement，and analysis of AM broadcast reradiation by power lines［S］．New York:IEEE，Inc．，1996．

［5］Zhang Xiaowu，Tang Jian，Zhang Huanguo，et al．Reradiation interference computation model of high voltage transmission line to the shortwave radio direction finding station［A］．20th International Zurich Symposium on E-lectromagnetic Compatibility，IEEE Electro-magnetic Compatibility［C］．Zurich，Switzerland，2009.309-312．

［6］Gan Zheyuan，Liu Xingfa，Zhang Guangzhou，et al．Research on protecting distance between AM receiving stations and UHV AC TL［A］．IEEE APEMC［C］．Singapore，2008.803-806．

［7］Tang Bo，Wen Yuanfang，Zhao Zhibin，et al．Computation model of the reradiation interference protecting distance between radio station and UHV power lines［J］．IEEE Transactions on Power Delivery，2011，26(2): 1092-1100．

［8］唐波，文远芳，张小武，等 (Tang Bo，Wen Yuanfang，Zhang Xiaowu，et al．)．中短波段输电线路无源干扰防护间距求解的关键问题 (Key problems of solving reradiation interference protecting distance between power transmission line and radio station at MF and SF) ［J］．中国电机工程学报 (Proceedings of the CSEE)，2011，31(19):129-137．

［9］C W Trueman，S J Kubina．Fields of complex surfaces using wire grid modeling［J］．IEEE Transactions on Magnetics，1991，27(5):4262-4267．

［10］S U Hwu，R Wilton．Electromagnetic scattering and radiation by arbitrary conducting wire/surface configurations ［A］．Antennas and Propagation Society International Symposium［C］．Syracuse，America，1988.890-893．

［11］D M Pozar，E H Newman．Analysis of a molopole mounted near an edge or a vertex［J］．IEEE Transactions on Antennas Propagation，1982，30(3):401-408．

［12］国家电力公司 (State Grid)．DL/T 691-19高压架空送电线路无线电干扰计算方法 (DL/T 691-19 methods of calculation of radio interference from high voltage overhead power transmission lines)［M］．北京:中国标准出版社 (Beijing:Standard Press of China)，1999．

Resonance characteristics and its impact factors of reradiation interference on radio station from UHV power lines

TANG Bo1，ZHANG Jian-gong2，WANG Hui-li3，GE Guang-zu1，LIU Xing-fa2
(1．College of Electronic Engineering＆New Energy，China Three Gorges University，Yichang 443002，China; 2．China Electric Power Research Institute，Wuhan 430074，China; 3．Sanmenxia Power Supply Company of Henan Electric Power，Sanmenxia 210098，China)

There is the resonance phenomenon in the reradiation interference on radio station from UHV power lines．IEEE gives the resonance mechanism and its frequency at the frequency band of 535～1705 kHz．In order toresearch the resonance characteristics of reradiation interference at higher frequency，the wire-surface simulation model excited by vertical polarization plane wave，in which steel tower is represented as surface model and ground wire is represented as wire model，is used．Based on the method of moments(MoM)，the base function of wiresurface model junction point and the computation method are discussed，and the interference values are calculated at the frequency band of 0.5～50.5MHz．The possible impact factors of interference resonance，such as ground wire，conductor，number of towers and tower spans，are studied．The results show that the decisive impact factor on reradiation interference is tower spans．

UHV power lines;reradiation interference;resonance characteristics;wire-surface model;method of moments;impact factor

TM723

A

1003-3076(2014)06-0063-06

2012-07-06

国家自然科学基金(51307098)、湖北省自然科学基金(2012FFB03701)资助项目

唐 波(1978-)，男，湖北籍，副教授，博士，研究方向为输变电系统电磁环境与超特高压输电技术;张建功(1975-)，男，湖北籍，高级工程师，硕士，研究方向为输变电系统电磁环境。