基于量子行为粒子群优化算法-混沌神经网络的电力系统负荷预测

王冰山，周步祥，肖 贤，林 楠

(1．四川大学电气信息学院，四川成都610065;2．四川电力职业技术学院，四川成都610071)

基于量子行为粒子群优化算法-混沌神经网络的电力系统负荷预测

王冰山1，周步祥1，肖 贤1，林 楠2

(1．四川大学电气信息学院，四川成都610065;2．四川电力职业技术学院，四川成都610071)

提出了一种基于量子行为粒子群优化算法和混沌神经网络相结合的电力系统负荷预测方法。根据粒子群的量子行为特征，采用全同粒子系更新粒子的位置，改善传统的粒子群算法精度低、易发散、收敛速度慢等缺点。利用粒子群优化算法优化出混沌神经网络的权值和阈值，克服混沌神经网络参数确定难度大、速度慢的缺点。然后利用得到的权值和阈值，通过改进粒子群优化算法-混沌神经网络模型，得到预测日的相应时刻负荷值。最后通过实际应用，证明该方法有较高的预测精度和较好的准确性，具备一定的实际应用价值。

量子行为;粒子群;全同粒子;混沌神经网络;负荷预测

1 引言

电力系统负荷预测是电力系统调度、规划、供电等管理部门的基础工作，准确、有效的负荷预测不仅可以合理安排电网内部机组的启停、保持电网安全稳定地运行，还可以减少一些不必要的储备容量，合理安排检修计划，从而保证了正常的生产，有利于经济效益和社会效益的提高［1］。过去的几十年来，国内外学者将各种预测方法和模型运用到电力系统短期负荷预测中，使预测精度得到了很大的提高。文献［2］把粗糙集和神经网络结合建立短期负荷预测模型，采用粗糙集理论对各种影响负荷预测的因素变量进行识别，以此确定预测模型的输入变量;在此基础上通过属性约简和属性值约简获得推理规则集，再以这些推理规则构筑神经网络预测模型，并采用附加动量项的BP学习算法对网络进行优化，但是该方法没有对工作日和休息日的负荷预测加以区分，预测精度不够;文献［3］采用改进的粒子群算法和BP神经网络结合，提出了在算法迭代过程中，每个粒子会额外生成与迭代次数相同的粒子，并与当前粒子同方向不同速度飞行，利用适应度值保存粒子历史最优值。虽然也改善了粒子多样性，但这种方法是以显著增加计算量和牺牲系统内存为代价;文献［4］使用PSO算法优化基函数中心和宽度，再用最小二乘法确定隐含层与输出层间的权值，最后将改进算法应用于时间序列的预测中。但该方法初始粒子群随机产生，会导致算法收敛速度的不确定性，降低算法的平均收敛速度;文献［5］采用混沌神经网络对短期负荷进行预测，但是仅运用混沌时间序列分析作为神经网络日峰值预测模型选择最佳嵌入维数和延迟时间的必要理论依据，其不足之处是仅局限于日峰负荷预测，同时对于混沌网络的权值和阈值的确定较为困难且速度慢。

本文采用量子化粒子群算法不仅通过全同粒子系改善了初始种群的质量，而且通过对粒子的全局最优值与粒子的局部最优值的比较，限制粒子陷入局部最小搜索状态，提高粒子的局部搜索能力，节省了搜索时间，使粒子能够快速地搜索到最佳位置，从而增强了算法的局部寻优能力和收敛速度及计算精度;利用优化后的粒子群算法确定混沌神经网络的权值和阈值，克服混沌神经网络参数确定难度大、速度慢的缺点。本文在建立负荷预测模型的时候，考虑了休息日和工作日的日负荷不同的特点建立新的预测模型，提高了预测的精度。

2 基本粒子群算法及其改进

2.1 基本粒子群优化算法描述

在基本粒子群算法中，种群是由n个粒子组成的，粒子i的信息表示为d维向量［6］。位置用xi= (xi，1，xi，2，．．．，xi，d)(i=1，2，．．．，n)表示，速度为vi= (vi，1，vi，2，．．．，vi，d)(i= 1，2，．．．，n)，pi= (pi，1，pi，2，．．．，pi，d)表示第i个粒子的最优位置，其他向量类似。速度和位置更新公式为:

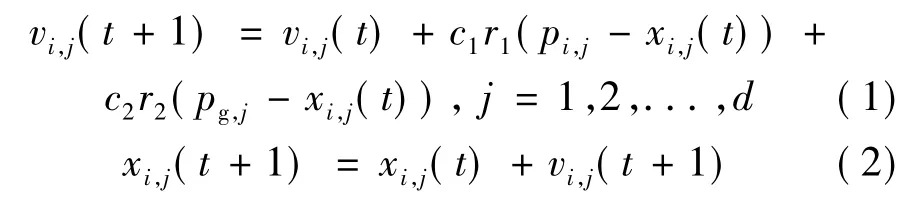
其中，vi，j(t)是粒子i在第t次迭代中第j维的速度;c1，c2是加速系数(或称学习因子)，控制粒子群向全局最好粒子和个体最好粒子方向飞行的最大步长，适当的c1，c2取值能够加快粒子群的收敛速度并且使粒子群不易陷入局部最优;r1，r2是［0，1］之间的随机数;xi，j(t)是粒子i在第t次迭代中第j维的当前位置;pi，j是粒子i在第j维的个体极值点的位置;pg，j是种群在第j维的全局极点的位置。粒子的每一维速度v控制在(vmin，i，vmax，i)之间。vmax，i如果过大，粒子将会飞离最优解，太小将会陷入局部最优。假设将搜索空间的第d维定义为区间(xmin，i，xmax，i)，每一维都用相同的设置方法。

2.2 量子行为粒子群优化算法

在基于量子行为的粒子群优化算法中，粒子的量子态通过波函数ψ(r，t)来表示。当ψ(r，t)确定后，粒子的所有力学分量和测值概率都可以确定，即xi，j(t)是由ψ(r，t)2决定的。在量子力学理论中，将属性相同的粒子称为全同粒子，由于全同粒子系具有交换对称性的特点，使得波函数具有很大的限制。一般来说，全同粒子系的波函数 ψ (q1，q2，．．．，qn)不一定表示粒子pi，j的本征态，所有的pi，j处于完全平等的地位。然而，所有pi，j的共同本征态是存在的，即是完全对称波函数和完全反对称波函数。

全同粒子系的波函数约束条件为:

根据蒙特卡洛方法，粒子群的运动等式可以转化为式(4)，另外引入式(5)和式(7)。

其中，C为常数因子;p，α，Mbesti分别根据式(5)、(6)和(8)求取;u∈[0，1]，为随机数据;α为t变量收缩因子，随着时间的变化而变化。

其中，α1和α2为t变量收缩因子的初值和终值;Tmax表示最大迭代的次数。根据经验数据，通常取α1= 2.5，α2=0.5，因此α∈(0．5，2．5)。pg，j表示每一个粒子全局搜索的最佳位置;pi，j表示每个粒子局部搜索到的最优位置;M表示种群的大小。

3 混沌神经网络模型

混沌神经元结构图如图1所示。

图1 混沌神经元结构图Fig．1 Chaotic neuron structure diagram

其中，vij、wij分别是第j个神经元的输入连接权值和反馈连接权值，xj(t+1)是神经元的输出［7］。

混沌神经元的输出函数为:

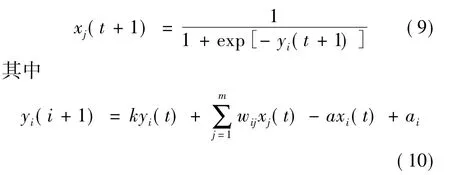
式中，a表示神经元之间的联接强度，也称耦合因子。

在混沌神经网络结构中，包括输入层、隐层和输出层。其中，隐层的每一个神经元都会受到外部输入和内部反馈的影响，通过不停地调节神经元的权值和阈值，得到合适的混沌神经网络模型［8］。

其中，xi是单个混沌神经元的输出值;wo是输出层神经元的阈值;wi是输出层神经元的权值;n1为隐层神经元的个数［9］。假设网络外部输入时间序列为u(t)，隐层输出为o(t)，网络输出为y(t)，混沌网络表示为:

f1采用Sigmoid函数，即:y=1/［1+exp(－x)］;f2采用线性函数:1W、2W和HW分别为输入层至隐层、隐层至输出层以及隐层节点之间的连接权矩阵。

混沌神经网络的输出函数为:

4 基于量子行为粒子群优化算法-混沌神经网络负荷预测

4.1 基本原理

本文采用的混合算法中，将粒子群的位置向量x作为混沌神经网络的节点间连接权值和阈值，在每次的迭代过程中，利用优化后的粒子群算法求出权值和阈值，然后利用混沌网络，求出对应的权值和阈值的实际输出值fk(k=1，2，．．．，n)(n是神经网络输入输出的样本对数)。

粒子的适应度函数为:

式中，yk是混沌神经网络的目标输出;fk是混沌神经网络的实际输出。

4.2 混合算法模型

针对电力系统的负荷具有周期性的特征，同时工作日和休息日的日负荷不同的特点，本文采用的模型如图2所示，采用多输入、单输出［10］。

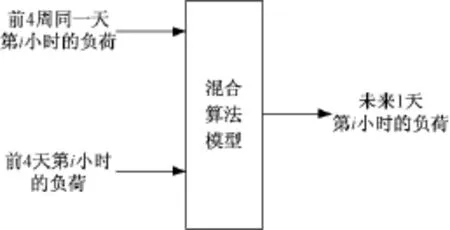
图2 混合算法模型输入和输出关系图Fig．2 Hybrid algorithm input and output diagram

对于混沌网络的隐层节点数的确定采用经验公式:

其中，n1为输入层节点数;n2为输出层节点数;N为修正值。根据多次实验结果，同时保证运算的速度，当n=5时，运算速度和结果的误差能够满足需要。本文中，取n=5。

CFG桩复合地基由于其承载力高、地基变形小、工程造价低等优良特性。目前，在高层和超高层建筑中得到广泛应用。但在CFG桩复合地基的设计中，由于对基本概念不清楚，有些设计人员提供给做复合地基设计的岩土工程师的资料不全面，给设计带来很多困难；或在设计过程中对一些参数的取值范围不明确，造成设计失误。给工程造成损失。为此本文就CFG桩复合地基设计中常见问题进行分析和探讨，以规范设计，提高其安全性和合理性。

4.3 算法分析

在混合算法中，首先是将神经网络的权向量和阈值作为粒子群搜索空间中位置元素，然后应用粒子群优化算法计算出神经网络的权向量和阈值，即求出每一个粒子相应的实际输出值 ok(k=1，2，．．．，n;n是神经网络输入输出的样本对数)。第i(i=1，2，．．．)个粒子的适应度函数为:

其中，yk是神经网络的目标输出。

本文采用平均绝对百分误差EM和均方根误差ER作为评估指标［11］。

4.4 粒子群-混沌神经网络混合算法的流程

(1)根据网络的输入和输出关系，初始化混沌网络的拓扑结构［12］。确定粒子的初始位置xi，j(0)和速度，确定粒子数M、最大允许迭代次数Tmax、加速系数c1和c2;

(2)如果是基本粒子群优化算法则用式(1)和式(2)对每一个粒子的速度和位置进行更新;如果是具备量子行为的粒子，采用改进粒子群优化算法，用式(7)和式(8)分别确定每个粒子的全局最优位置、局部搜索位置;

(4)利用混沌神经网络计算出每个粒子对应的个体极值，将粒子群中个体极值最好的作为全局极值。记录该粒子的序号，用gbest(全局极值点)表示最好粒子的当前位置;

(5)根据粒子的适应度函数，计算每一个粒子的适应度值。如果粒子的适应度值优于该粒子的个体极值，则将pbest(个体极值点)设置为该粒子的位置，同时对粒子的个体极值进行更新。当全部粒子的个体极值优于此时的全局极值时，将gbest设置为该粒子的位置，记录该粒子的序号，同时对全局极值进行更新;

(6)判断是否满足流程结束条件。如果当前位置满足预定要求(迭代次数达到了给定的最大次数或达到最小误差要求)时，则停止迭代，输出最优解;如果不能满足结束条件，转到步骤(2)。

4.5 数据的归一化处理

为了确保输入量具有较好的作用，选用Sigmoid函数中间段的函数关系，从而避开其两端的饱和区域，必须对神经网络的输入量进行归一化处理［13］。

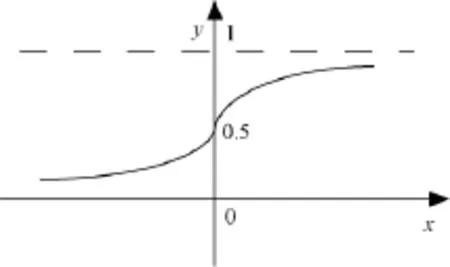
图3 Sigmoid函数曲线图Fig．3 Sigmoid function curve

t时刻负荷数据采用如下归一化公式:

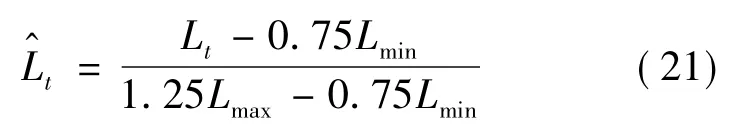
在输出层则用式(22)重新换算回负荷值:

式中，Lmax和Lmin分别为训练样本集中负荷的最大值和最小值。

5 应用实例及结果

本文预测模型中混沌神经网络的反馈过程是通过循环实现的，其停止的条件用精度来判断，即如果A(t)－A(t－1)＜eps，则停止反馈，得出输出值。其中A(t)是当前时刻的隐层输出值，A(t－1)是上一时刻的隐层输出值。初始参数分别为:c1=2和c2= 2.4，粒子群数M=80，最大迭代次数Tmax=5000。

本文结合某地的实际情况，对其某日24h整点的电力负荷分别采用量子粒子群算法、混沌学习算法和本文提出的量子粒子群优化-混沌神经网络算法进行预测，评估指标对比情况如表1所示，负荷预测结果如表2所示。

由表1可知，量子粒子群-混沌学习算法在训练550次左右的EM值已经小于量子粒子群算法和混沌学习算法训练2500次的EM值。量子粒子群-混沌神经网络算法在训练1500次的EM值也小于量子粒子群算法和混沌学习算法训练5000次时的EM值，所用时间前者80s，后两者的时间分别为213s和256s。可见在收敛性和训练速度上，本文采用的混合算法优势明显。三种算法预测结果与实际值的平均百分绝对误差对比图如图4所示。

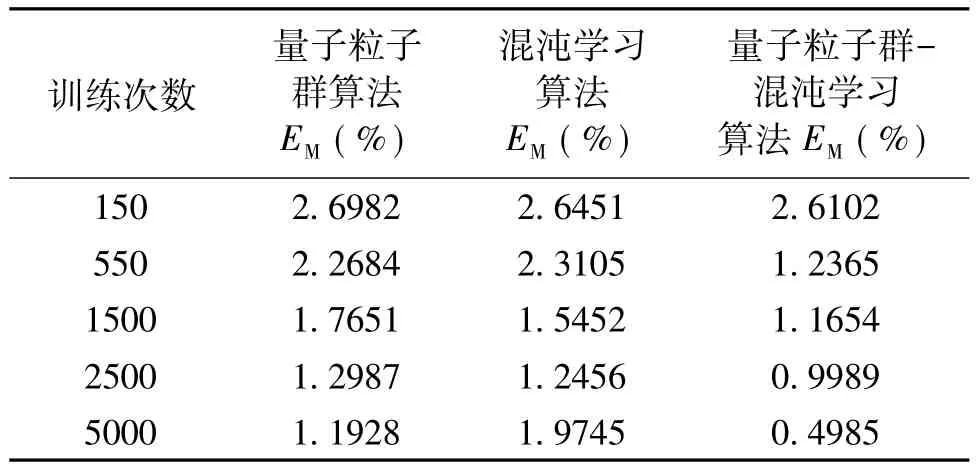
表1 评估指标对比表Tab．1 Evaluation index comparison table

图4 EM值比较Fig．4 EMvalue comparison

对比表2中预测结果和相对误差可知，采用量子粒子群-混沌神经网络算法训练400次时的负荷预测结果精度已经好于采用量子粒子群算法(3000 次)和混沌学习算法(2000次)时的预测精度，表明本文采用的预测方法和模型在预测精度和速度方面，明显好于以上两种算法。

从图5可以看出，本文采用的量子粒子群-混沌神经网络的混合算法预测结果相对误差控制在4%以内，且误差波动较小。预测精度比量子粒子群算法和混沌学习算法要好很多。

从图6中可以看出，当迭代次数达到900时，量子粒子群-混沌神经网络算法的适应度函数就基本达到稳定。而量子粒子群算法和混沌学习算法迭代次数达到1700和2000次左右时候才达到稳定。将粒子群的适应度函数设定为训练误差，适应度函数越大，输出误差越大。由此可见，本文采用的混合算法模型的辨识精度远高于其他两种算法模型的辨识精度，表明本文采用的模型更加实用。

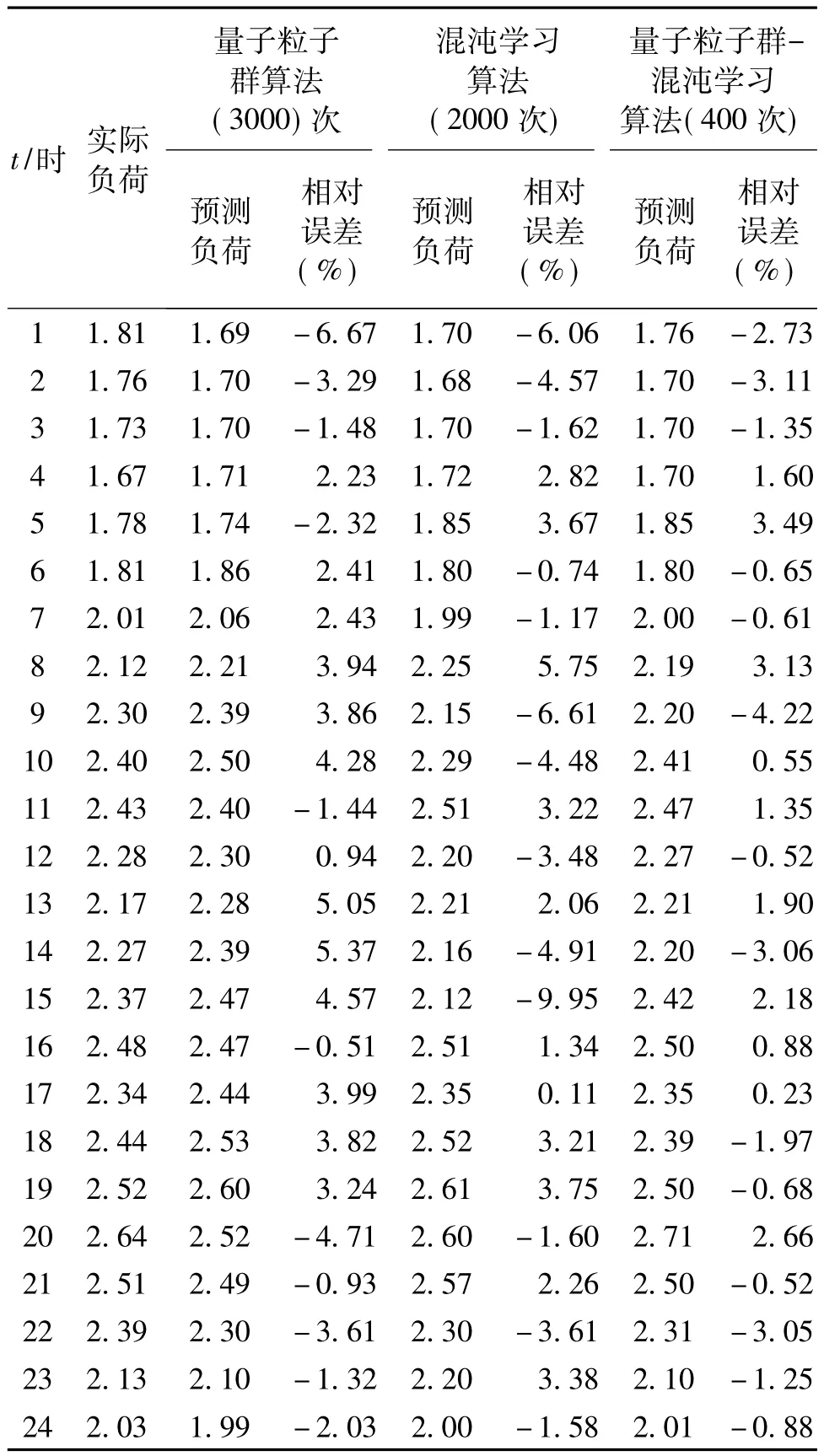
表2 预测结果比较Tab．2 Comparison of forecasting results

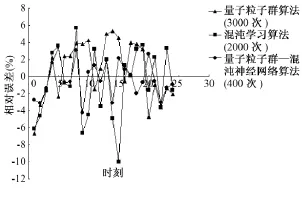
图5 负荷预测的相对误差Fig．5 Relative error of load forecasting

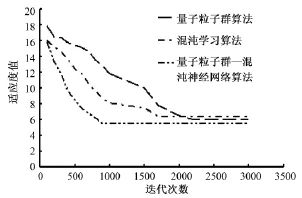
图6 适应度函数值比较Fig．6 Fitness function value comparison

6 结论

本文提出的基于量子行为粒子群优化算法-混沌神经网络的电力系统负荷预测的方法，解决了传统量子粒子群算法收敛速度慢、易发散的缺点，解决了混沌学习算法预测精度低、数据获得困难的不足。根据工作日和休息日的日负荷特性的不同，建立新的预测模型。实际应用表明，与传统的预测方法相比，本文提出的预测方法是一种有效的、可行的负荷预测方法。

［1］师彪，李玉侠 (Shi Biao，Li Yuxia)．基于改进粒子群-模糊神经网络的短期电力负荷预测 (Short-term load forecasting based on modified particle swarm optimizer and fuzzy neural network model) ［J］．系统工程理论与实践 (Systems Engineering－Theory＆Practice)，2010，30(1):157-166．

［2］刘学琴，吴耀华，崔宝华 (Liu Xueqin，Wu Yaohua，Cui Baohua)．基于扩展粗糙集的短期电力负荷预测模型 (Short-term load forecasting model based on extended rough set)［J］．电力系统保护与控制 (Power System Protection and Control)，2010，38(5):25-28．

［3］乔维德 (Qiao Weide)．基于改进PSO-BP神经网络的短期电力负荷预测研究 (Study of short-term load forecasting based on improved PSO-BP neutral network model)［J］．电力系统保护与控制 (Power System Protection and Control)，2007，35(7):17-21．

［4］毕洪波，张玉波 (Bi Hongbo，Zhang Yubo)．混沌RBF神经网络在电力负荷预测中的应用 (The application of chaotic RBF neural network in power load forecasting) ［J］．科学技术与工程 (Science Technology and Engineering)，2012，24(9):7389-7412．

［5］徐明义 (Xu Mingyi)．混沌神经网络在短期电力负荷预测中的应用 (Application of chaotic neural networks in short-term load forecasting)［J］．电力系统保护与控制 (Power System Protection and Control)，2010，18 (15):125-128．

［6］雷绍兰，孙才新 (Lei Shaolan，Sun Caixin)．电力短期负荷的多变量时间序列线性回归预测方法研究 (The research of local linear model of short-term electrical load on multivariate time series) ［J］．中国电机工程学报(Proceedings of the CSEE)，2006，26(2):25-29．

［7］张涛，赵登福，周林 (Zhang Tao，Zhao Dengfu，Zhou Lin)．基于RBF神经网络和专家系统的短期负荷预测方法 (Short-term load forecasting using radial basis function networks and expert system)［J］．西安交通大学学报 (Journal of Xi'an Jiaotong University)，2011，35 (4):331-334．

［8］靳雁霞，韩燮，周汉昌 (Jin Yanxia，Han Xie，Zhou Hanchang)．改进的粒子群优化算法 (Improved particle swarm optimization algorithm) ［J］．计算机工程与设计 (Computer Engineering and Design)，2010，30 (17):4074-4076．

［9］吴杰康，陈明华，陈国通 (Wu Jiekang，Chen Minghua，Chen Guotong)．基于PSO的模糊神经网络短期负荷预测 (Fuzzy neural network model based on particle swarm optimization for short-term load forecasting) ［J］．电力系统自动化学报 (Proceedings of the Electric Power System and Automation)，2007，19(1):63-66．

［10］唐俊杰，牛焕娜，杨明皓 (Tang Junjie，Niu Huanna，Yang Minghao)．基于线性相关分析的周期自回归短期负荷预测 (Periodic auto regressive short-term forecasting method based on the linear correlation analysis)［J］．电力系统保护与控制 (Power System Protection and Control)，2010，38(14):128-132．

［11］陈耀武，汪乐宇，龙洪玉 (Chen Yaowu，Wang Leyu，Long Hongyu)．基于组合式神经网络的短期电力负荷预测模型 (Short-term load forecasting based on modular neural networks) ［J］．中国电机工程学报 (Proceedings of the CSEE)，2011，21(4):79-84．

［12］丁军威，孙雅明 (Ding Junwei，Sun Yaming)．基于混沌学习算法的神经网络短期负荷预测 (Short-term load forecasting based on chaos neural network learning algorithm)［J］．电力系统自动化 (Automation of Electric Power Systems)，2010，24(2):32-36．

［13］曾鸣，刘宝华，徐志勇 (Zeng Ming，Liu Baohua，Xu Zhiyong)．基于混沌模糊神经网络方法的短期负荷预测 (Short-term load forecasting based on artificial neutral network and fuzzy theory) ［J］．湖南大学学报 (自然科学版)(Journal of Hunan University(Natural Science))，2008，35(1):58-62．

Power system load forecasting based on quantum behavior particle swarm optimization algorithm-chaotic neural network

WANG Bing-shan1，ZHOU Bu-xiang1，XIAO Xian1，LIN Nan2(1．School of Electrical Engineering and Information，Sichuan University，Chengdu 610065，China; 2．Sichuan Electric Power College，Chengdu 610071，China)

This paper presents a combinative method of power system load forecasting based on quantum behavior particle swarm optimization and chaotic neural network．Based on the quantum behavioral characteristics of the particle swarm，and using the identical particle system to update the particle’s position，the shortcomings of the traditional particle swarm optimization，such as low accuracy，dissipation easy，and slow convergence rate can be avoided．Using particle swarm optimization algorithm to optimize the chaotic neural network weights and thresholds，we can overcome the shortcomings that it is difficult and slow to determine the parameters of chaotic neural network．U-sing the weights and thresholds，through the improved particle swarm optimization algorithm-chaotic neural network model，the corresponding time load value of the predicting date can be obtained．Finally，through the practical application，it can be proved that the method has higher prediction accuracy and better accuracy，with some practical value．

quantum behavior;particle swarm;identical particles;chaotic neural network;load forecasting

TM715

A

1003-3076(2014)06-0007-06

2013-03-26

王冰山(1988-)，男，河南籍，硕士研究生，研究方向为电力系统自动化及计算机信息处理、分布式电源等;周步祥(1965-)，男，四川籍，教授，博士，主要从事电力系统自动化、计算机应用等方面的研究工作。