风场群接入系统的静态电压稳定分析

刘文霞，吴方权

(1．贵州电网公司电网规划研究中心，贵州贵阳550003; 2．云南电网公司红河供电局，云南红河661000)

风场群接入系统的静态电压稳定分析

刘文霞1，吴方权2

(1．贵州电网公司电网规划研究中心，贵州贵阳550003; 2．云南电网公司红河供电局，云南红河661000)

大量风电场以集群形式接入电网，将对系统安全稳定运行带来一定的影响。为计算风电场群接入电力系统的静态电压稳定性，采用Nataf逆变换建立风场群相关风速模型，将风电场等效为一台风机，以负的负荷形式接入PQ节点。在风场群不同相关度的风速下进行连续潮流计算，将系统对应电压崩溃点作为系统负荷裕度，以分析系统静态电压稳定性。对接入风场的改进IEEE-14 及IEEE-30节点系统进行仿真计算，结果表明所提方法能有效分析风场群接入对系统静态电压稳定的影响，为系统分析设计、运行控制提供一定的参考。

连续潮流;风场群;Nataf逆变换;蒙特卡罗仿真;静态电压稳定;负荷裕度

1 引言

在全球大力倡导低碳经济、节能减排的环境下，电力系统大兴新能源发电，大量的风电场以集群［1］的形式接入传统电网中，这将对电力系统安全稳定运行带来新的挑战。本文就风场群接入电网进行静态电压稳定分析。

电力系统静态电压稳定常采用连续潮流CPF (Continuous Power Flow)进行分析［2］。大量文献采用CPF法计算系统的静态电压稳定性［3-5］，但是对于风电场群接入电网的静态电压稳定的研究较少。目前风场群的建模方法主要是建立时间尺度上具有相关性的自回归滑动平均模型法［6，7］和基于历史风速建立风场群风速相关矩阵的方法［8］。但是上述静态电压稳定的研究没有在连续潮流的计算中考虑风电场的集群效应，也没有分析风场群相关风速对系统静态电压稳定性的影响。

本文采用Nataf逆变换方法建立风场群相关风速样本，在连续潮流中运用蒙特卡罗仿真法计算系统SVSM值，分析比较了在风场群不同相关度的风速下的静态电压稳定性。改进IEEE-14和IEEE-30

算例充分验证了算法的有效性。

2 连续潮流计算静态电压稳定

连续潮流法是在给定负荷增长方式下，计算出一条潮流解的路径，即负荷节点的PV曲线。它满足系统扩展潮流方程［9］:

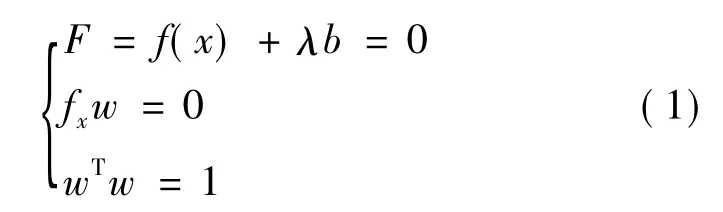
式中，f(x)=0为常规潮流方程;b、λ为负荷增长方式及增长参数;x(V，λ)为状态变量;w对应fx的零特征值的右特征向量。

负荷增长参数λ为0即对应系统的当前正常运行状态，负荷裕度是指电力系统当前运行点与静态电压稳定极限点之间的距离。用CPF计算静态电压稳定性时，常使用系统的负荷裕度来表征静态电压稳定性，如图1所示，即在采用CPF计算时，随着系统负荷水平的增长，节点电压逐渐降低，当系统节点电压没有足够的无功支撑时，系统电压出现崩溃，如图1中的“电压崩溃点”所示。

图1 负荷节点PV曲线及负荷裕度定义Fig．1 Load buses PV curve and definition to load margin

3 风场群建模

3.1 风速模型与风机模型

采用威布尔概率分布函数［10］来描述风速变化:

式中，v为风速;c和k为在风速模型数据矩阵中定义的常量，分别为尺度参数和形状参数。在满足工程实际要求的情况下，风机输出特性描述为分段函数形式:

式中，v为风速;vci是切入风速;vco是切出风速;vr是额定风速;Pr是风电机组的额定出力;n为风速-功率系数，理想值为3。

为简化模型，风场等效为一台发电机，将风电接入点作为一个随机变化的负的负荷处理。当风速已知，有功确定，风电场以某一功率因数运行时，风电场出口处无功功率可由下式求得:

式中，φ为负荷节点功率因数角。

3.2 风场群相关风速建模

地理位置较近的风场风速往往具有一定的相关性。在工程中，Nataf广泛用于结构可靠度的相关性计算［11］。本文将采用该技术来解决风场群相关风速的问题，由历史风速记录及风场位置可得经验的风场群中风速相关度ρVij，满足威布尔分布的各个风场风速为v=(v1，v2，…，vm)，vi(i=1，2，…，m)的概率密度函数为 fi(vi)，威布尔累积分布函数为 Fi(vi)，则通过等概率变换的原则，可以将相关系数为ρηij的相关标准正态分布向量η(η1，…，ηm)转换为相关系数为ρvij的相关性风速序列v的空间，该方法即为Nataf逆变换［12，13］，如下:

风速向量v的相关系数矩阵ρv与相关标准正态分布向量η的相关系数矩阵ρη的关系为:

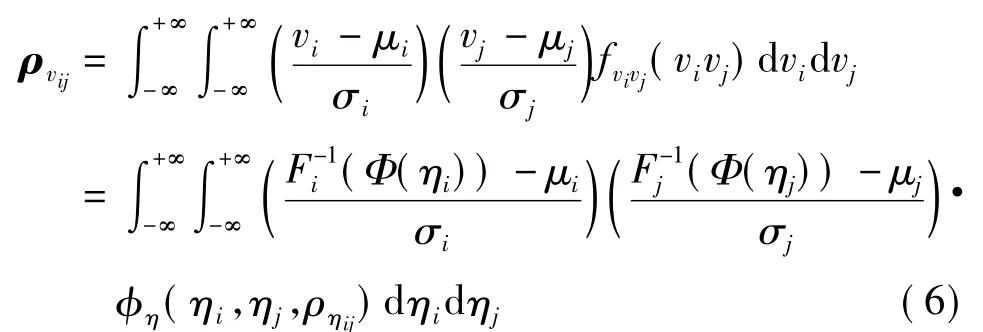
式中，η(·)为相关系数为ρηij的二维标准正态分布联合密度概率函数;μi为风速序列vi的均值;σi为vi的标准差。

由ρv与相关标准正态分布向量η的相关系数矩阵ρη的关系可求得相关的标准正态分布向量的相关矩阵ρη，对ρη作Choleskey分解:

生成独立的标准正态分布随机序列ξ，通过式(8)即可得到相关的标准正态分布向量η:

将所得相关的标准正态分布向量η代入Nataf逆变换式(5)即可建立风场群相关风速模型。

4 计算步骤

采用蒙特卡罗法进行仿真，每次蒙特卡罗计算包含两部分:采用Nataf逆变换技术建立风场群风速的模型;将所建风场群相关风速模型嵌入连续潮流计算中，进行连续潮流计算，得到系统负荷裕度，从而得到该运行状态下的系统静态电压稳定性。将蒙特卡罗计算结果作概率统计，得到系统的负荷裕度概率密度曲线、累积概率分布曲线等。具体计算过程如图2所示。

5 算例分析

5.1 算例一

采用改进的IEEE-14算例进行仿真计算，算例数据见文献［14］。14节点系统含有5个发电机节点、20条支路(含3条变压器支路)。现对负荷较重的节点4、5、9、14分别接入装机容量为198MW、198MW、49.5MW、49.5MW，单机容量为1.5MW。由于风场节点4、5相距较近，风场9、14相距较近，前者组成风场群1，后者组成风场群2。对系统在风场群不同风速相关度下进行连续潮流计算。

图2 计算流程图Fig．2 Calculation flow chart

系统在风场群不同相关度下计算得到负荷裕度均值如图3所示。可以看出，随着相关度的提高，系统负荷裕度增大。说明风场群中风电场之间的联系越紧密，电力系统的静态电压稳定也会得到一定的改善。

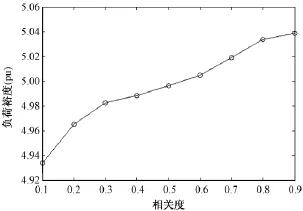
图3 IEEE-14节点系统中不同相关度下系统负荷裕度均值Fig．3 Mean of load margin in different correlation coefficients in IEEE-14

假设相关度0.1为低度相关，0.5为中度相关度，0.9为高度相关。采用蒙特卡罗仿真法，系统在风场群三个等级的相关度下计算得到负荷裕度的概率密度曲线如图4所示，累积概率分布如图5所示。随着风速相关度的增大，负荷裕度水平波动范围也随之增大，表现在图4中概率密度最高点的值，相关度为0.9时，概率密度最高点为0.35，而相关度为0.1时，概率密度最高点达到0.4。这主要是由于风速相关性较强时，风电场出现出力较大的可能性和波动的范围也随之增大。

图4 IEEE-14节点系统中不同相关度下系统负荷裕度概率密度Fig．4 Probability density of load margin in different correlation coefficients in IEEE-14

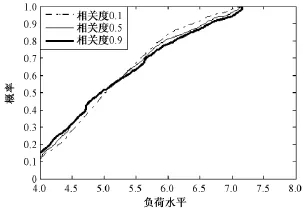
图5 IEEE-14节点系统中不同相关度下系统负荷裕度累积概率分布Fig．5 Cumulative distribution of load margin in different correlation coefficients in IEEE-14

5.2 算例二

IEEE-30节点算例系统中含有30节点，6台发电机，41条支路(37条线路支路，4条变压器支路)，在负荷较重而无电源点的12、14、15节点接入风电场，容量分别为150MW、99MW、180MW，单机容量均为1.5MW。这三个风电场地理位置相距较近，构成了一个风场群。对系统在风场群内不同风速相关度下进行连续潮流计算，得到了如图6所示的不同风速相关度下时系统负荷裕度均值。图7、图8分别为高、中、低相关度下系统负荷裕度的概率密度曲线及累积概率分布曲线。IEEE-30节点算例所得计算结果与IEEE-14节点算例近似。说明风场群风速相关性对系统静态电压稳定性有一定的影响。

图6 IEEE-30节点系统中不同相关度下系统负荷裕度均值Fig．6 Mean of load margin in different correlation coefficients in IEEE-30

图7 IEEE-30节点系统中不同相关度下系统负荷裕度概率密度Fig．7 Probability density of load margin in different correlation coefficients in IEEE-30

图8 IEEE-30节点系统中不同相关度下系统负荷裕度累积概率分布Fig．8 Cumulative distribution of load margin in different correlation coefficients in IEEE-30

6 结论

为分析风场群接入电力系统的静态电压稳定性，采用Nataf逆变换法生成风场群具有一定相关性的风速，从而建立风场群模型，在蒙特卡罗仿真中运用连续潮流法计算得到系统的负荷裕度来量化静态电压稳定性。分析了不同风场群相关度的风速对系统静态电压稳定性的影响。IEEE-14及IEEE-30节点系统验证了算法的有效性与实用性。

本文所提方法能为大型风场群接入电力系统的静态电压稳定计算提供一种有效的建模分析方法，为稳定分析提供重要的参考。

［1］肖创英，汪宁渤，丁坤，等 (Xiao Chuangying，Wang Ningbo，Ding Kun，et al．)．甘肃酒泉风电功率调节方式的研究 (System power regulation scheme for Jiuquan wind power base) ［J］．中国电机工程学报(Proceedings of the CSEE)，2010，30(10):1-7．

［2］徐玉琴，刘文霞，潘雄 (Xu Yuqin，Liu Wenxia，Pan Xiong)．MLRM法预估含风电场系统静态电压稳定裕度 (MLRM-based estimation of static voltage stability margin of power systems with wind farms)［J］．电力系统保护与控制 (Power System Protection and Control)，2013，41(5):48-53．

［3］孙宏斌，李钦，张明晔，等 (Sun Hongbin，Li Qin，Zhang Mingye，et al．)．基于动态潮流方程的连续潮流模型与方法 (Continuation power flow method based on dynamic power flow equation) ［J］．中国电机工程学报 (Proceedings of the CSEE)，2011，31(7):77-82．

［4］马幼捷，张继东，周雪松，等 (Ma Youjie，Zhang Jidong，Zhou Xuesong，et al．)．基于分岔理论的含风电场电力系统静态电压稳定问题研究 (Study on steady state voltage stability of power system containing wind farm based on bifurcation theory) ［J］．电网技术(Power System Technology)，2008，32(9):74-79．

［5］吴昊，卫志农，王成亮，等 (Wu Hao，Wei Zhinong，Wang Chengliang，et al．)．基于连续潮流综合算法的电压稳定性研究 (Voltage stability study based on synthesis method of continuous power flow)［J］．电力系统保护与控制 (Power System Protection and Control)，2011，39(6):99-104．

［6］Chen P，Pedersen T，Bak-Jensen B，et al．ARIMA-based time series model of stochastic wind power generation［J］．IEEE Trans．on Power Systems，2010，25(2):667-676．

［7］穆安乐，刘宏昭，张彦斌，等 (Mu Anle，Liu Hongzhao，Zhang Yanbin，et al．)．风力发电机三维阵风谱建模与仿真的向量自回归法 (VAR approach for 3-D gust wind spectral modeling and simulation of wind turbine) ［J］．中国电机工程学报 (Proceedings of the CSEE)，2008，28(8):117-120．

［8］张粒子，凡鹏飞，麻秀范，等 (Zhang Lizi，Fan Pengfei，Ma Xiufan，et al．)．考虑调峰适应性风险的风电场群时序规划方法 (Timing planning method for investment of clustering wind farms considering risk of peak load regulation) ［J］．中国电机工程学报 (Proceedings of the CSEE)，2012，32(7):14-22．

［9］刘明波，谢敏，赵维兴 (Liu Mingbo，Xie Min，Zhao Weixing)．大电网最优潮流计算 (Optimal power flow computing of large-scale power systems)［M］．北京:科学出版社 (Beijing:Science Press)，2010．272-281．

［10］Bowden G J，Barker P R，Shestopal V O，et al．The Weibull distribution function and wind power statistics［J］．Wind Engineering，1983，(7):85-98．

［11］吴帅兵，张坤，李典庆 (Wu Shuaibing，Zhang Kun，Li Dianqing)．相关非正态变量变换时相关性变化对可靠度的影响 (Effect of correlation change from transformation of correlated abnormal variables on structural reliability)［J］．武汉大学学报 (Engineering Journal of Wuhan University)，2011，44(2):151-155．

［12］Juan M Morales，Antonio J Conejo，Juan Pérez-Ruiz．Simulating the impact of wind production on locational marginal prices［J］．IEEE Trans．on Power Systems，2011，26(2):820-828．

［13］Juan M Morales，L Baringo，Antonio J Conejo，et al．Probabilistic power flow with correlated wind sources［J］．IET Generation，Transmission＆Distribution，2010，4 (5):641-651．

［14］Zimmeraman R D，Gan D．MATPOWER:a Matlab power system simulation package［CP/OL］．2005-02-14．http://www．pserc．cornell．edu/matpower．

Static voltage stability analysis of power systems with wind farm groups

LIU Wen-xia1，WU Fang-quan2
(1．Grid Planning＆Research Center，Guizhou Power Grid Cooporation，Guiyang 550003，China; 2．Yunnan Honghe Electric Power Supply Bureau，Honghe 661000，China)

High penetrations of wind farm groups will produce certain effect on power system’s safety and stablility．In order to analyze the static voltage stability of power system with wind farm groups，this paper applies inverse Nataf transformation to build correlated wind speed of wind farm groups，and wind farms which are equalized as wind turbines will connect to PQ buses as negative loads．Continuous Power Flow will compute system’s voltage collapse points which are served as load margin in different wind speed correlation coefficients so as to analyze static voltage stability．The case study on the improved IEEE-14 and IEEE-30 buses system demonstrates the effectiveness of the method，and it provides certain reference to power system analysis and operational control．

continuous power flow;wind farm groups;inverse Nataf tansformation;Monte Carlo simulation;static voltage stability;load margin

TM71

A

1003-3076(2014)06-0013-05

2012-10-24

中国南方电网公司重点科技项目(K-GZ2013-468)

刘文霞(1987-)，女，贵州籍，助理工程师，硕士，研究方向为电力系统分析计算、运行控制;吴方权(1986-)，男，贵州籍，助理工程师，主要从事电力信息化管理、电力系统通信相关工作。