苯酚含量预测的高斯过程回归模型

王 鑫 李红丽

(江南大学教育部轻工过程先进控制重点实验室，江苏 无锡 214122)

0 引言

双酚A(Bisphenol-A，BPA)是生产环氧树脂、聚砜树脂、聚碳酸酯、聚苯醚树脂、不饱和聚酯树脂等多种高分子材料的一种关键原料，也是生产涂料、抗氧剂、增塑剂、阻燃剂、热稳定剂、橡胶防老剂、农药等精细化工产品的一种重要化工材料［1］。因此，BPA作为一种重要的化工原料，近年来越来越受到人们的重视。苯酚作为BPA生产过程的中间体，苯酚含量的实时监测对BPA生产过程的控制是十分重要的。由于BPA生成过程极其复杂，因此很难对该过程建立结构确定的参数模型，且苯酚的含量是很难直接在线测量的。

根据BPA生产过程的以上特点，本文提出了一种基于高斯过程回归的苯酚含量预测方法。高斯过程回归模型是一种贝叶斯非参数模型［2－3］。贝叶斯非参数模型是一种定义在无限维参数空间上的贝叶斯模型，它可以自动地适应自身接收到的数据，事先不用指定模型的大小和参数的个数。贝叶斯非参数模型非常适合于集成来自多个传感器的数据，以及基于观测数据选择合适的模型大小。这些特点使得高斯过程回归模型特别适合用于长期持续监测。

1 相关的工作

为了在线监控苯酚含量等与生产过程关系密切的化工参数，有如下两种传统做法:①采用在线分析仪表对难以测量的参数进行分析的方法，这种方法设备投资大、维护成本高，并且测量滞后较大，使得调节品质有所下降;②采用间接的质量指标对难以测量的参数进行控制的方法，如精馏塔灵敏板的温度控制、温差控制等，但这种方法难以保证最终质量指标的控制精度。

目前也有一些基于软测量的模型。如文献［4］使用最小二乘支持向量机算法(LS-SVM)在线建立估计模型。虽然该模型能够适应不断变化的工况，但是由于不同的测试样本选择的局部样本集不同，提取的主成分特征也不同，因此每次都需要重新确定LS-SVM参数，测试时间较长，不能满足实际化工生产过程的应用。文献［5］提出了基于疏密部数据划分的多模型软测量方法。该方法虽然模型跟踪性和泛化能力较好，但是模型比较复杂，而且建模过程中在确定邻域半径时，要根据数据分布情况，自行确定占有率和可调系数，具有很大的随机性。一旦确定半径有偏差，就会直接影响边界阈值的大小，可能导致模型与实际相差甚远。文献［6］提出了一种基于仿射传播聚类和高斯过程的多模型建模方法。该方法虽然具有较高的估计精度，但是模型过于复杂。

2 高斯过程回归模型

2.1 高斯过程回归

假设给定训练数据集 D={(xi，yi)|i=1，2，…，n}，其中xi表示训练数据集D中的第i个输入向量，yi表示训练数据集D中的第i个目标输出，n表示训练数据集中样本的个数。高斯过程回归模型是对输入向量与目标输出之间的关系f进行推断，即在给定输入向量时确定目标输出的条件分布。

假定f是一个高斯过程，即 f～GP( m，k)，f是一个以m为均值函数、k为协方差函数的高斯过程。高斯过程是一个随机过程［7］。与高斯分布类似，高斯过程完全由其均值函数与协方差函数确定。

根据高斯过程的定义可知，f( x1)、f(x2)、…、f(xn)服从多元高斯分布，且该多元高斯分布的均值向量为m( xi)，协方差矩阵为K，因此:

实际目标输出y往往会包含一些噪声:

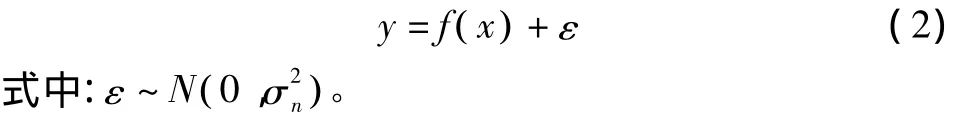
于是，问题转化为已经观测到训练数据集D:yi=f( xi)+ εi，i=1，2，…，n，需要在测试数据集 D*={( xi*，yi*)|i=n+1，n+2，…，n+n*}预测对应的 输出值f*。

训练数据集的输出向量y和测试数据集的预测值f*的多元高斯分布为:

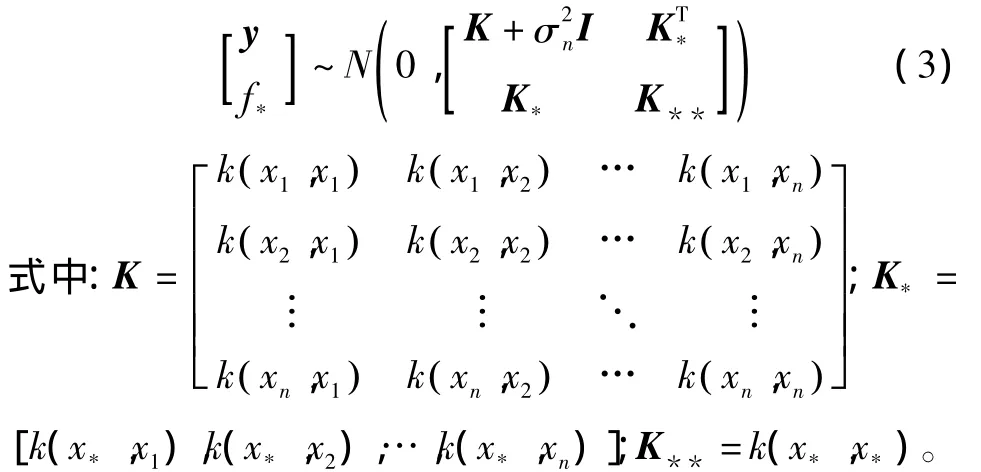
根据多元高斯分布的条件分布形式，可得出高斯过程回归预测方程的关键式为:

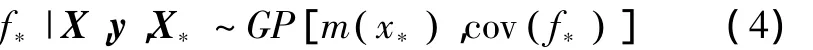
式中:矩阵X由训练数据集输入xi的列向量组成;矩阵X*由测试数据集的输入xi*的列向量组成。

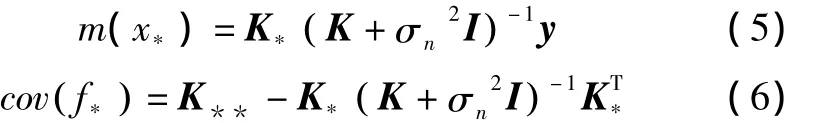
2.2 超参数选择

根据以上分析可知，协方差函数k对于高斯过程回归分析是至关重要的。在高斯过程中，协方差函数k必须满足Mercer条件。常用的协方差函数为平方指数函数［8］，其形式如下:

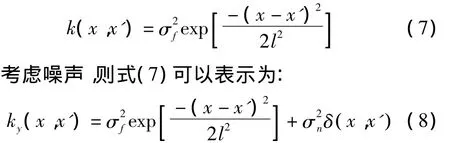
从式(8)可以看出，参数 σf、σn、l对新输入的输出预测值y*影响较大。设超参数 θ= { l，σn，σf}，对 θ进行优化调整。本文通过极大似然法来获得协方差函数的优化后的超参数θ。对于上述给定的ky(x，x')，其训练样本的对数边缘似然函数为:

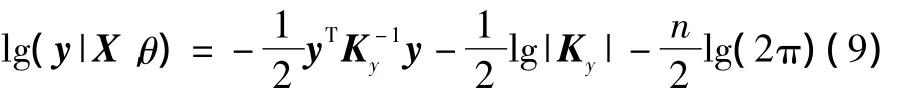
在极大似然估计框架下，需要通过不断调整超参数θ，使得训练样本的对数边缘似然函数取得最大值。在优化过程中，需要计算 lg［p( y|X，θ)］对 θ的偏导数，并令偏导数为0，获得最优超参数θ。

3 工业实例研究

3.1 工况介绍与数据描述

根据对精馏塔C303的工艺流程和现场分析，选择了C303塔内的液位、温度、塔底出料的温度及由前一单元V304软测量模型的估计变量(苯酚、BPA、BPA-24的浓度)这6个输入辅助变量;并选择了精馏塔C303塔底的苯酚浓度为输出的主导变量。辅助变量的实时数据是通过现场的集散控制系统(DCS)获得的，主导变量的样本数据通过每天人工分析值获得。本文采集了2009年、2010年的共233组数据作为训练样本，2011年的100组数据作为测试样本。针对长达3年的数据情况，采用基于贝叶斯非参数模型的高斯过程回归模型分析预测2011年苯酚浓度的输出值，并将其与2011年真实的输出值相比较。为了评价模型性能，本文使用平均相对误差(MRE)和最大相对误差(MXRE)来描述，MRE用来度量估计值与真实值的总体偏离情况，MXRE用来度量估计值与真实值偏离的最大幅度。它们的定义分别如下:

式中:yx和y分别为该模型预测的输出值和2011年真实的输出值。

3.2 特征选择

一般来说，特征选择的目标主要有3个:①改善预测模型的预测性能;②更有效的预测模型;③更好地从数据理解生成数据的过程［9－10］。

本试验已测得的特征有6个，考虑到特征个数并不大，以输出目标的均值为界，将回归问题变成一个二元分类问题。然后，接收者按照操作特征(receiver operating characteristic，ROC)准则对这6个特征进行排序。

3.3 模型设置

完成特征排序之后，本工业实例设置高斯过程的均值函数为零常函数，协方差函数为平方指数函数，似然函数为高斯函数。然后，根据式(9)，进行超参数优化，确定优化后的超参数。最后，使用优化后的待训练模型对训练样本进行训练，确定模型参数。

3.4 试验结果

将训练所得模型对测试样本进行测试，真实值与估计值的对比曲线如图1所示。

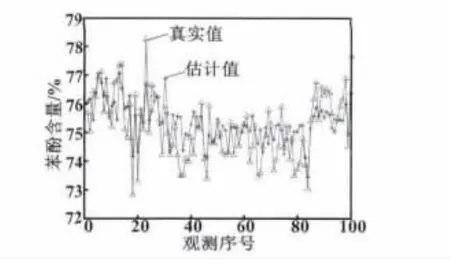
图1 预测结果与真实值的对比曲线Fig.1 The comparison curves between the prediction results and the actual values

各个测试样本点的相对误差值曲线如图2所示。

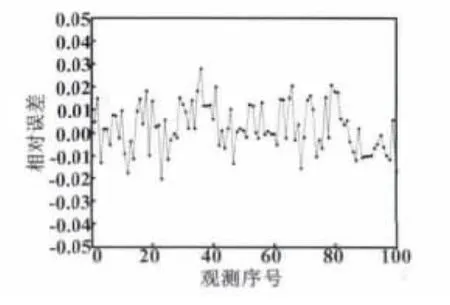
图2 相对误差值曲线Fig.2 The relative errors curve

不同方法的性能比较如表1所示。由表1可以看出，本文提出的模型在MRE与MXRE这两个指标方面都优于其他模型。

表1 不同方法的性能比较Tab.1 Performance comparison of different methods

4 结束语

在仅进行了简单的特征排序与仅使用了单一模型的情况下，本文使用高斯过程回归模型在苯酚含量预测中取得了较好的预测效果。这主要是因为作为贝叶斯非参数模型，高斯过程能够根据数据自适应地调整模型结构与参数个数。这就巧妙地避免了其他方法中模型选择与模型组合的难题。试验结果表明，对于双酚A生产过程等很难使用参数模型进行建模或求解的过程，高斯过程回归模型可以作为一种有效的建模手段。

［1］程沧沧，邓南圣，吴峰，等.光电催化降解双酚A的研究［J］.华中师范大学学报:自然科学版，2005，39(3):365－369.

［2］龙健颜，卢素，刘金山.贝叶斯非参数回归模型及非参数似不相关回归模型的应用［J］.统计与决策，2011，27(16):17 －20.

［3］Kottas A，Behseta S，Moorman D E，et al.Bayesian nonparametric analysis of neuronal intensity rates［J］.Journal of neuroscience methods，2012，203(1):241 －253.

［4］李雅芹，杨慧中.一种局部KPLS特征提取的LSSVM软测量建模方法［J］.计算机工程应用，2011，47(21):235 －238.

［5］梅振益，杨慧中.基于疏密部数据划分的多模型软测量［J］.江南大学学报:自然科学版，2010，9(5):521 －525.

［6］李雅芹，杨慧中.基于仿射传播聚类和高斯过程的多模型建模方法［J］.计算机与应用化学，2010，27(1):51 －54.

［7］奚宏生.随机过程引论［M］.合肥:中国科学技术大学出版社，2009.

［8］Rasmussen C E，Williams C K I.Gaussian processes for machine learning［M］.Cambridge:the MIT Press，2006.

［9］Guyon I，Elisseeff A.An introduction to variable and feature selection［J］.Journal of Machine Learning Research，2003，32(4):1157 －1182.

［10］杨慧中，章军，陶洪峰.基于互信息的软测量变量选择［J］.控制工程，2012，19(4):562 －565.

［11］王黎明，陈颖，杨楠.应用回归分析［M］.上海:复旦大学出版社，2008:1－30.

［12］方开泰，全辉，陈庆云.实用回归分析［M］.北京:科学出版社，1988:64－103.