有限状态自动机产生式推理的一般性建模方法

彭翔王飞

(华侨大学信息科学与工程学院，福建 厦门 361021)

0 引言

利用自动机构建离散事件动态系统(discrete event system，DES)诊断模型是一种基于模型的诊断方法［1］。自动机模型的可诊断性［2］以及对于更为复杂的DES诊断的建模［3］都是在此基础上做延伸。基于Petri网模型的DES故障诊断推理［4－5］也是当今DES故障诊断的研究热点。在故障诊断推理中，利用穷举法列出系统的所有状态，而后剔除不必要的状态进行诊断［6］，这对较为庞大的系统而言是比较繁琐的。文献［7］利用自动机对故障推理进行建模，但没有给出其泛化的建模方式，因此，很难运用到实际多样化的系统中。

针对现今越来越庞大复杂的系统，系统故障的产生式规则也愈加繁琐，本文提出了采用自动机对故障诊断专家系统推理一般性建模的方法。这种方法对于复杂判别规则较多的产生式推理均适用。此外，还给出了建模后的简化方法，并用实例验证了该方法的可行性。

1 确定性有限状态自动机与推理机

定义1 一个确定性有限状态自动机(deterministic finite state automata，DFSA)定义为一个五元组［8］:

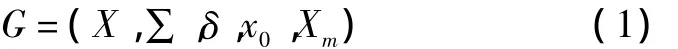
式中:X为非空有限状态集;∑为有限事件集;δ为状态转移函数;x0∈Xm为初始状态;Xm∈X为标志状态集。

定义2 对有限自动机G和任一状态x0∈X，∑*为输入符号串集合，则自动机G产生的语言L(G)定义为使状态转移函数δ(ω，x0)为输入符号串ω∈∑*的一个集合［8］，也即:

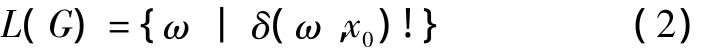
规则产生式一般由if与then语句构成，如果用DFSA描述一条规则产生式的推理过程，那么可以将if之后的一个条件作为DFSA的一个事件。满足这个条件，即事件发生，将转移到相应的状态，这个状态即表示此条件满足，可以进行下一步推理。如果一条规则需要有多个条件同时满足才触发，那么多个条件则对应多个事件。这些事件都发生，则表明对应的所有条件都满足，触发规则，进入终止状态，此状态即代表推理结束。

借助DFSA的定义，就可以归纳出产生式推理到有限状态自动机的映射关系。

①产生式推理有一个开始状态，表示系统准备就绪，可以开始接收条件进行推理，这对应的就是DFSA的初始状态。

②产生式的推理过程是接收条件的过程，推理的结束是使得产生式规则中的某个规则触发。当接收一系列条件，直至这些条件中存在的某些条件使得这些条件构成的某一规则成立，则该规则触发，推理结束。在DFSA中，事件就是读入的条件，每个条件都作为一个事件，状态则描述从初始状态到当前状态的所经过的所有事件，即满足所有条件。这样，产生规则中的所有规则就可以用DFSA中的事件状态序列描述。

③在产生式推理过程中，接收到之前已经接收过的条件或接收到与之前条件无规则关联的条件，则推理原地等待。

在DFSA中，当接收到之前接收过的条件时，则发生了之前发生过的事件，则在原状态上构造一个自转移，使得自动机仍然在当前状态;当接收到与之前条件无规则关联的条件时，相当于没有对应的状态转移函数，DFSA保持当前状态不变。

④产生式推理的结束是某个规则的触发。在DFSA中，推理结束则转移到终止状态。在终止状态之前的事件状态序列，就是某一规则中的所有条件的满足过程。

根据以上映射关系，可以赋予自动机五元组新的含义，使其成为推理机:

式中:X为有限非空状态集合，表示满足某个规则的某些条件后到达的已满足条件状态;∑为有限事件集合，一条规则产生式的一个条件为一个事件，条件满足，则事件发生;δ为状态转移函数;x0为初始状态，表示推理机准备就绪，可以开始推理;Xf为终止状态，推理完成状态，若到达此状态，表明触发某规则。

由以上定义的推理机以及前述的产生式推理与有限状态自动机的映射关系，得到其“且”、“或”、自转移的逻辑表达，具体表达方式如以下示例所示。

① 逻辑“a且b”关系图如图1所示。

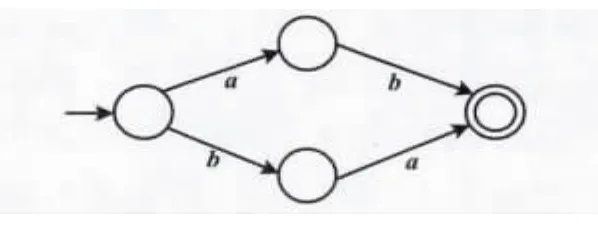
图1 “a且b”关系图Fig.1 Relationship of a and b

② 逻辑“a或b”关系图如图2所示。

图2 “a或b”关系图Fig.2 Relationship of a or b

③自转移关系图如图3所示。

图3 自转移关系图Fig.3 Self-transition relationship

2 一般性建模流程

定义3 整齐规则:对于含有多条规则产生同种结果的推理，这些规则中的条件数都是相等的，则称之为整齐规则。

这里所述的规则产生式是由其对应的所有条件通过“与”关系组合，进而触发规则的。若条件之间含有“或”关系，则另建立“或”对应关系的新规则。建模具体流程如下所述。

假设某系统有m条规则产生式，每条规则产生式有nm个条件。其中nm代表第m个规则拥有的条件数。

①根据前述推理机的定义构造m个推理机，则每个推理机对应其中的一条规则。第m条规则所对应的状态事件序列如图4所示。

图4 第m条规则的状态事件序列Fig.4 State-event sequences of rule m

这里描述的只是一条规则中的一个推理路径，从xm0到xmnm之间，若有n个条件，则应当有条推理路径，其中为n的全排列。

②整合多条规则后的综合推理机的状态事件序列流程如图5所示。先做以下定义:E为所有规则中所有条件的集合;Em为第m条规则的所有条件的集合;Eold为流程图中执行循环操作后已使用过的规则中的所有条件集合;xmn为第m条规则中满足第(n－1)个条件后的状态;emn为第m条规则中的第n个条件;Emn={emn丨xm(n+1)=(xmn，emn)}。上述定义中的 m，n=0，1，2，3，…，且不依托于规则中条件之间的先后关系。

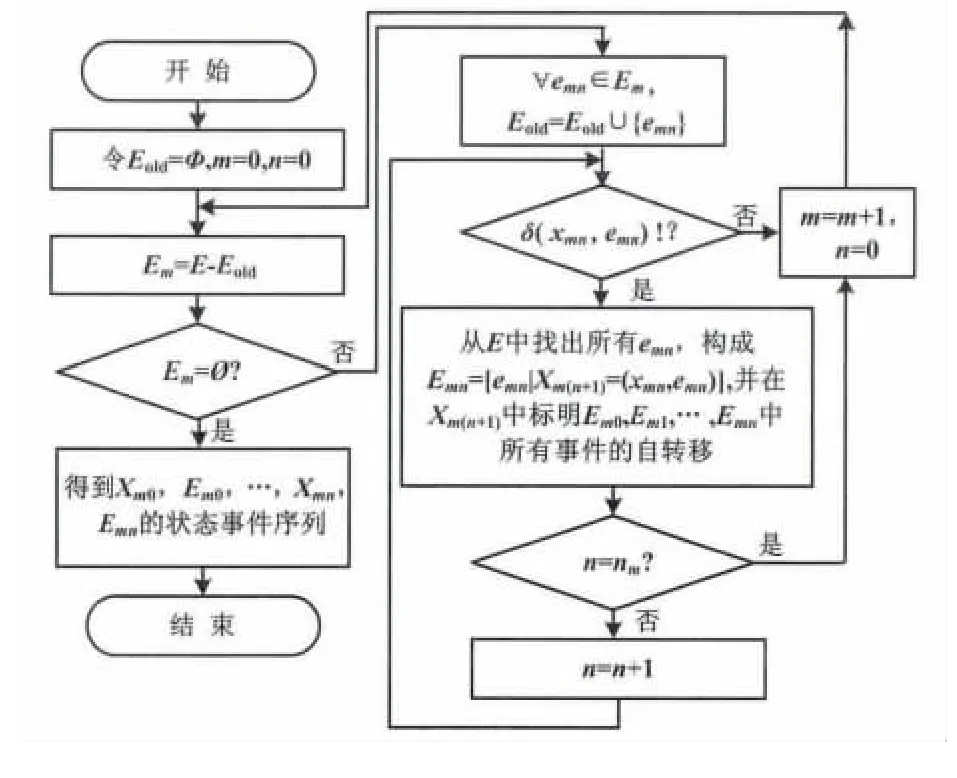
图5 构造状态事件序列流程图Fig.5 Flowchart of forming state-event sequences

③通过以上流程，可以获得推理过程的状态事件序列，进而构造推理机。其中x0=x00=x10=…=xm0，合并后得到初始状态x0，在Emnm后加入状态xf，表示推理结束的终止状态。至此推理机建模完成。

当描述的产生式规则为整齐规则且这些规则有一些具有相同的条件时，可以利用输入等价［9］原则进行状态合并，状态合并后其上的自转移事件也取并集。这样就使得模型得到简化，从而提高推理效率。

3 实例验证与分析

“设备”和“断路器”表示的电力网络的拓扑结构如图6所示［10］。本实例旨在对输电线路故障位置的诊断的推理，所以这里的“设备”为“输电线路”与“母线”。

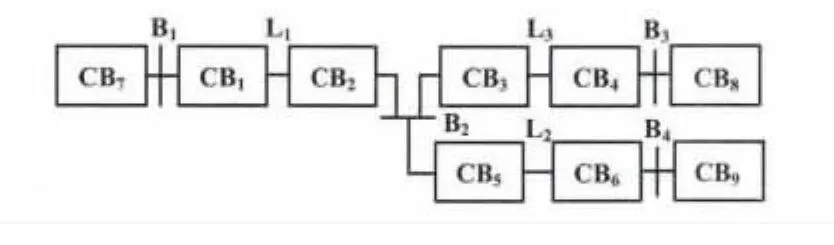
图6 电力网络实例模型Fig.6 Instance model of electricity network

图6中，L1～L4代表线路，CB1～CB9为断路器，B1～B4为母线。

当故障发生时，相应点的线路保护动作，线路保护动作引起对应的断路器动作，切除故障点与电网的联接，从而达到保护电网的目的;同时，当故障发生时，数据采集与监视控制系统(SCADA)会采集各线路保护动作与断路器动作的数据。通过采集得到的数据来定位故障点则由相关推理系统完成。线路故障的产生式规则［11］如表1 所示，推理方式为 if“前件1”and“前件2”then“后件”。

表1 保护动作与断路器动作的产生式规则Tab.1 Production rules of actions of protection and circuit breaker

由以上产生式规则，可以构建相应推理机。保护动作与断路器动作所对应的事件表如表2所示。

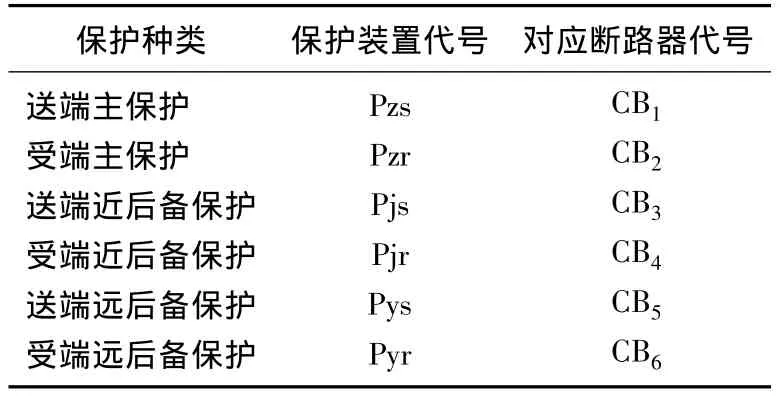
表2 保护动作及对其应断路器动作事件表Tab.2 Event list of protection and corresponding circuit breaker

首先，以规则1为例，构造的基于单条产生式规则的推理机如图7所示。

图7 规则1的推理机Fig.7 Inference engine of rule 1

其次，由综合推理机建模流程图，构造综合状态事件序列。

最后，由于本例的产生式规则是整齐规则，加入初始和推理结束状态后，可以利用输入等价原则进行状态合并，减少状态空间维数。简化后的基于表1规则产生式的最终推理模型如图8所示。

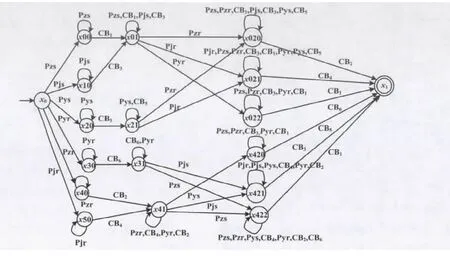
图8 最终推理模型Fig.8 The final inference model

在电力网络实例模型中，当输电线路某处发生故障时，若SCADA系统采集到断路器CB1、CB3、CB5的动作信息，并采集到线路L1的送端主保护、L2的送端远后备保护和L3的送端远后备保护动作，则根据当前的故障信息，结合图6可知，可能是线路L1或母线B3故障，但是无法分清到底是哪一个故障。这时，将采集的故障信息输入到上述构建的推理模型中，此时模型中事件 Pzs、CB1、Pyr、CB6发生，使得自动机模型从初始状态x0转移到了终止状态xf，这意味着故障发生。

由于本文所建立的是输电线路故障诊断模型，所以结果表示输电线路L1发生故障，至此诊断结束。同样地，若是建立了关于母线B3的故障诊断的自动机模型，在L1发生故障的情况下，将不会到达故障发生的终止状态。

4 结束语

本文采用确定性有限状态自动机研究了基于规则产生式的推理，在给出基于自动机模型的推理机的基础上，提出了基于多条规则产生式的自动机推理模型的泛化建模流程。同时，给出了建模的具体流程图，并利用输入等价原则进行简化。最后，对本文提出的建模流程进行实例验证，将模型应用在输电线路故障诊断的产生式推理过程中，获得了较好的效果。这种推理模型也可以作为故障诊断专家系统的辅助决策系统，具有较好的现实意义。

［1］Cassandras C，Lafortune S.Introduction to discrete event systems［M］.Boston MA:Kluwer Academic Publisher，1999.

［2］Sampath M，Sengupta R，Lafortune S，et al.Diagnosability of discreteevent systems［J］.IEEE Transactions on Automatic Control，1995，40(9):1555－1575.

［3］Gascard E，Simeu-abazi Z.Modular modelling for the diagnostic of complex discrete-eventsystems［J］.IEEE Transactions on Automation Science and Engineering，2013(99):1 －23.

［4］Wu Z，Hsieh S.A realtime fuzzy Petri net diagnoser for detecting progressive faults in PLC based discrete manufacturing system［J］.The International Journal of Advanced Manufacturing Technology，2012(61):405－421.

［5］Cabasino M P，Giua A，Lafortune S，et al.A new approach for diagnosability analysis of petri nets using verifier nets［J］.IEEE Transactions on Automatic Control，2012(12):3104 － 3117.

［6］Costa N S，Coury D V，Pereira W D C.Finite automata applied to a classification of fault in an eletric power system［C］∥Transmission ＆Distribution Conference and Exposition，Latin America，2006:1 －5.

［7］王书振，李雷，王保保.基于有限状态自动机的产生式推理［J］.仪器仪表学报，2008，29(8):372 －374.

［8］郑大钟，赵千川.离散事件动态系统［M］.北京:清华大学出版社，2001.

［9］Ware S，Malik R.Conflict-preserving abstraction of discrete event systems using annotated automata［J］.Discrete Event Dynamic System，2012(22):451－477.

［10］杨建维.基于模糊Petri网的电网故障诊断方法研究［D］.成都:西南交通大学，2011.

［11］方培培.Perti网理论在电力系统输电网络故障诊断［D］.天津:天津大学，2005.