贝叶斯网络在生产过程故障诊断中的应用

肖 坤 杨马英

(浙江工业大学信息工程学院，浙江 杭州 310023)

0 引言

现有故障诊断［1］方法主要有基于数学模型［2］、基于知识［3］和基于信号处理这3类方法［4］。它们各有各的特点和局限性。基于数学模型的方法需要比较准确的对象模型。基于知识的方法不需要精确模型，但理论尚待完善。基于信号处理的方法诊断效果高度依赖于过程数据。

复杂过程可能出现的故障呈现多样性，将多种诊断方法进行有机融合有助于准确和及时地进行故障诊断。贝叶斯网络通过概率表达变量间的因果关系，便于进行知识推理。通过适当的节点设置对于诊断由复杂不确定因素引起的故障具有优势。为此，本文提出一种基于贝叶斯网络的生产过程故障诊断方案，并通过对田纳西-伊斯特曼(Tennessee Eastman，TE)过程的仿真实例，验证贝叶斯网络在故障诊断方法集成和提高诊断准确率方面的有效性。

1 贝叶斯网络的设计

贝叶斯网络［5－7］是基于概率论和图论的一种不确定性知识表达推理模型。贝叶斯网络是一个有向无环图，其中节点代表研究对象中的变量，有向弧代表变量间的因果关系，变量之间的关系度量用节点间的条件概率来表示。定性信息是通过网络的拓扑结构表达的，而定量信息则是通过节点间的概率密度来表示。

贝叶斯网络设计的核心在于网络结构设计和参数的确定。

1.1 网络结构及节点的设计

定义故障诊断的贝叶斯网络B(G，P)为有向无环图，节点包括X和E两种类型。其中G=(X，E)。P指条件概率表(conditional probability tables，CPT)。X={X1，X2，…，Xi}为随机变量集合。变量X的CPT说明条件分布P［X|Parents(X)］，Parents(X)为 X的双亲，用于表达各个信息要素之间的影响程度。

在故障诊断中，节点变量可以是任何问题的抽象，如设备部件状态、测量值、观测现象、意见征询等。本文选取系统控制变量和检测变量作为状态节点变量。在连续过程的故障诊断中，首先分析系统各故障类型会引起的非正常变化的状态变量，以确定状态变量节点集合;再根据状态变量节点之间的相互作用建立因果贝叶斯网络。

将不同的单一故障诊断方法对系统诊断得出的故障发生概率，以网络节点的形式添加到基本贝叶斯网络中。在贝叶斯推理时，节点E作为已知证据，即在已知单一故障诊断方法对系统诊断得出故障发生概率的条件下，进一步通过网络推理得出故障最终发生的概率。

故障诊断贝叶斯网络模型如图1所示。

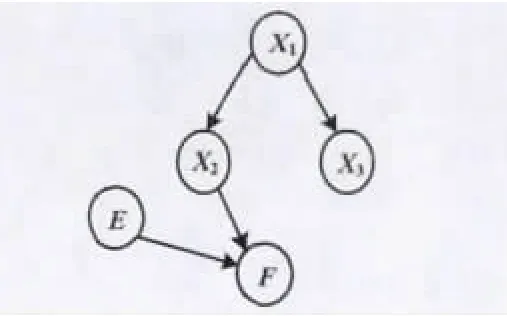
图1 故障诊断贝叶斯网络模型Fig.1 Bayesian network model for fault diagnosis

1.2 贝叶斯参数学习算法

当贝叶斯网络结构确定后，如何确定已知结构的参数就是从数据中学习参数的问题。即利用给定样本数据去学习网络的参数的概率分布，从而更新网络变量原有的先验分布。学习方法主要分为两大类:基于经典统计学的学习和基于贝叶斯统计学的学习［8］。

基于贝叶斯统计学的学习的基本思想是:给定一个含有未知参数的分布P(C|θ)以及一个完整的实例数据集D，随机变量θ具有一个先验分布P(θ)，代表事先知道的θ的信息;然后通过在数据集D上的学习，参数的信息发生了变化，表示后验概率P(θ|D)，并以P(θ|D)作为参数估计的依据。

在故障诊断中，各状态节点的值为连续值，子节点Xi+1受父节点Xi影响。当Xi异常变化时，Xi+1必然也异常变化。因此，可将Xi+1是否异常的概率表示为Xi+1偏离正常范围的程度，偏离越大，Xi+1异常的概率越大，据此可求得状态节点之间的后验概率。当故障节点的父节点Xi异常的概率越大，F发生的概率也越大，即F后验概率可通过节点Xi求得。而证据节点E的后验概率则用某单一故障诊断方法对系统的故障工况的诊断率来表示。此诊断率为故障诊断方法对系统单一故障的综合诊断率，是一个定值，故可用E的先验概率表示。

本文在贝叶斯统计学的参数学习算法基础上，提出通过计算状态节点后验概率P(θ|D)的概率公式来实现贝叶斯网络参数学习。该公式建立在能够事先收集系统在正常工况和故障工况时状态变量的完整数据集的前提下，可用来计算状态变量当前值异常的概率。

我们首先根据事先收集的系统在正常工况和故障工况时状态变量X的完整数据集DX，计算得到状态变量的先验分布P(θx|DX)，分析参数变量θx分布，求得正常工况时DX均值EX和故障工况时的DX最大值max_DX和最小值min_DX信息。据此设定判断θx正常与否的阈值 θC。

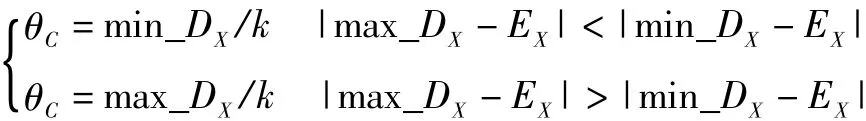
式中:参数k为0～1的常数，其取值依赖于人为经验，本文k取0.8;θC根据系统历史数据求得。

当参数变量θX值为θC时，故障概率为100%，可见θC是反映变量偏离正常状态程度的一个指标。变量 θX离 θC越近，发生故障的概率越大;变量 θX离 θC越远，发生故障的概率越小。

据此可得后验概率P(θ|D)公式为:

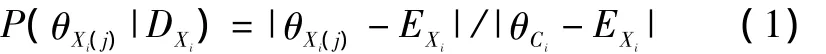
式中:θXi(j)为当前检测得到的节点Xi的数据变量;i=1，2，…，n 为网络中对应的节点号;j=1，2，…，m 为采样时刻。

在贝叶斯网络中，将第一个采样数据点根据以上公式求得的概率作为状态节点先验概率，单一故障诊断方法对系统的诊断率作为证据节点的先验概率，即可建立初始概率表CPT。随着状态节点采样数据点的更新，初始条件概率表CPT已经不再反映节点之间的关联，故用数据进行参数学习，根据式(1)更新状态节点后验概率来更新CPT，从而实现贝叶斯网络参数学习的目的。

2 贝叶斯推理

贝叶斯推理［9］的目的是通过联合概率分布公式，在给定的网络结构和参数的条件下，计算某一事件发生的概率。在故障诊断中，推理过程就是通过已知的系统运行状态参数推断出系统故障的过程。常见的推理方法分为精确推理和近似推理。精确推理包括:联合树(junction tree，JT)算法、图约简算法、组合优化算法等。联合树算法是目前计算速度快、应用广的贝叶斯网络精确推理算法;但它对网络的规模有限制，适用于单连通和多连通网络的推理。本文所建立的应用于故障诊断的贝叶斯网络拓扑结构固定、规模不大，因此选用联合树算法。

联合树是一种由团集C中元素Ci和边集S中元素Sj连接而成的树结构。其中，团和边满足JT特性，即任何两个Ci和Cj之间路径上的每个团包含在Ci∩Cj内，相邻两个团之间的边Sij=Ci∩Cj。

联合树算法的基本思路是，先将BN转换为一种二次结构(second structure，SS)，再通过对SS推理得到BN推理的精确结果。为将BN上推理转换为SS上推理，必须将对应的有向无环图G转变为联合树JT=(C，S)，其转换过程包括如下4 个步骤［9］。

①建立BN的Moral图。建立Moral图的过程就是找出每一个节点的父节点，并将它们用无向边两两相连，同时将所有有向边改为无向边。

②三角化Moral图。在Moral图中添加一些无向边，将其每一个等于或大于4的环的两非相邻节点连接起来，完成Moral图的三角化。

③确定所有的团。对三角化后的Moral图，找到构成联合树的所有团。团是三角化后Moral图中的最大全连通子图，团中每对不同的节点都有边相连。

④建立联合树。在找到的团中添加一些边和分隔节点就可构造一棵联合树。联合树须满足:树中连接任意两个团C和C'的路径上的所有团节点必须包含变量C∩C'。

联合树算法过程如图2所示。

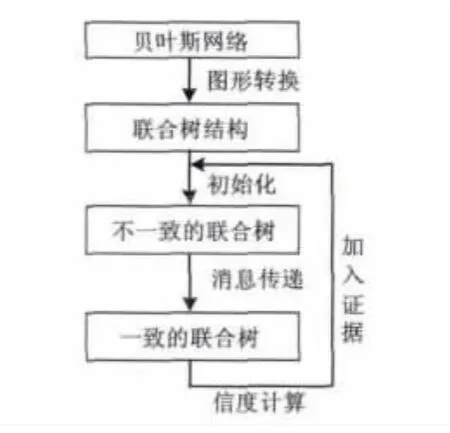
图2 联合树算法过程图Fig.2 Process diagram of the junction tree algorithm

将贝叶斯网转化为联合树后，就要为联合树的所有节点指定参数，即对联合树进行初始化。联合树初始化后，要在联合树上进行消息传递。通过各团节点之间的消息传递，可以使联合树达到全局一致，即达到稳态。

当一个联合树通过消息传递满足全局一致性后，即可计算任意随机变量X的概率分布。

在故障诊断中，当证据E=e加入时，要重新进行证据收集和证据扩散的过程，直到得到全局一致的联合树为止。当联合树再次达到全局一致时，对任意的团节点C有:Φc=P(C，e)(e表示加入的证据)。

计算故障变量节点F的概率分布，首先要找到任意一个包含节点F的团节点C，然后对其进行边缘化，得到以下表达式:

最后根据节点概率公式，求得变量节点F的概率分布为:

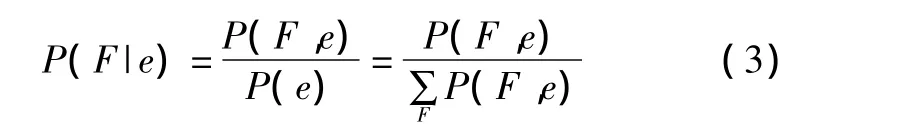
通过上述联合树推理算法，即可在已知单一故障诊断方法对系统诊断得出故障发生概率的条件下，进一步通过网络推理得出故障最终发生的概率。

3 仿真试验

TE过程是Downs［10］等人提出的一个模拟实际化工过程的标准问题，它较好地反映了复杂工业过程的特点，很适合于研究过程控制和故障诊断技术。其工艺流程图如图3所示。

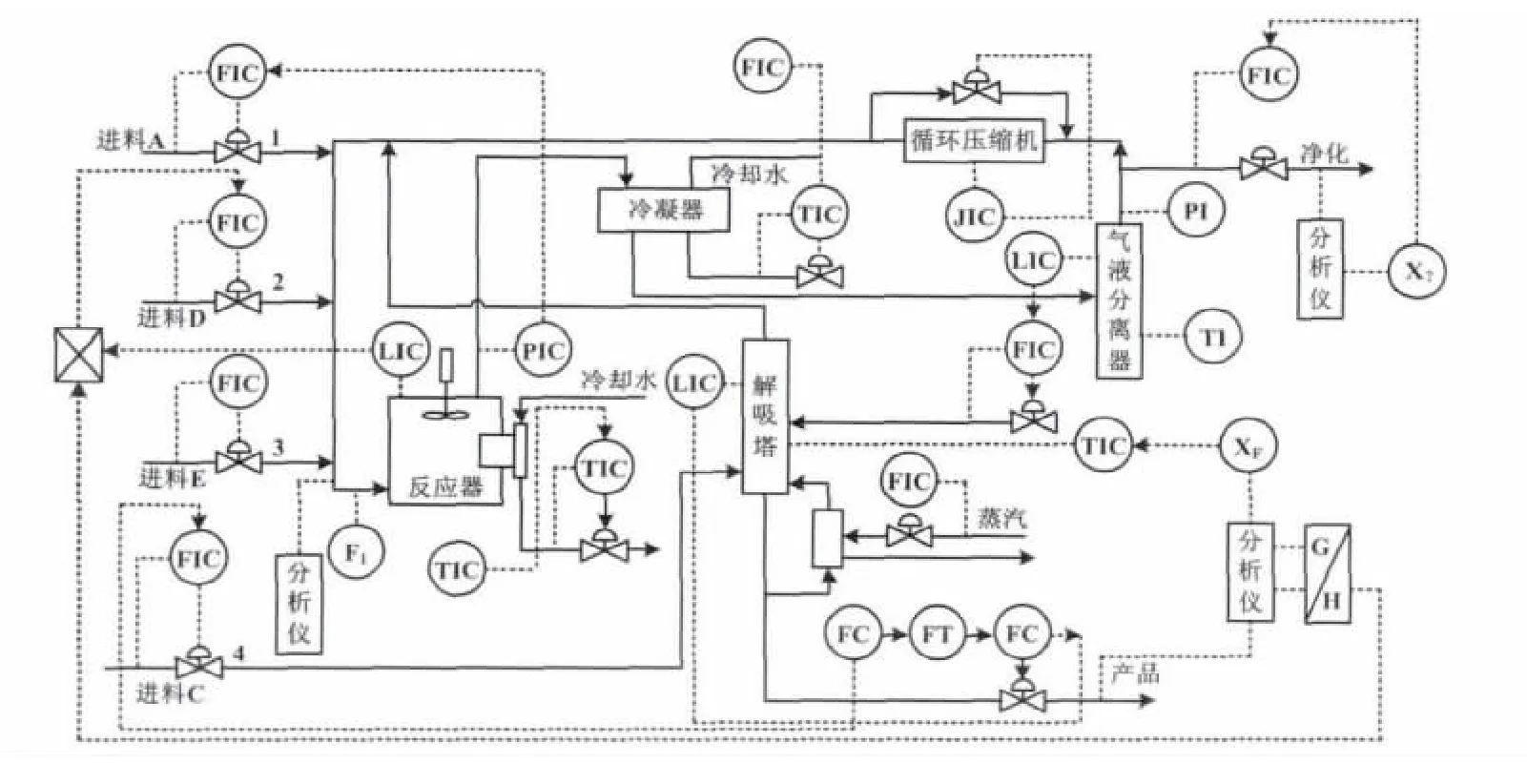
图3 田纳西-伊斯特曼过程流程图Fig.3 Flowchart of Tennessee Eastman process

TE过程包括41个测量变量和12个控制变量(记为X1～X53)。仿真模型包括21个预设定的故障。本文采用文献［11］的控制方案，在正常工况和模拟故障1，2，4，9 的情形下(具体如表 1 所示)，得到闭环系统仿真数据。

表1 TE故障描述Tab.1 Fault descriptions of TE process

机器学习法中的概率神经网络［12］(PNN)及支持向量机［13］(SVM)算法属于基于信号处理的方法，目前已广泛应用于故障诊断研究中。基于PNN的故障诊断方法实质上是利用PNN模型的强大的非线性分类能力，将故障样本空间映射到故障模式空间中，从而形成一个具有较强容错能力和结构自适应能力的诊断网络系统。基于SVM的故障诊断方法是通过某种事先选择好的非线性映射将输入向量映射到一个高维特征空间，在这个空间构造最优分类超平面，从而实现对故障的分类。本文选用这两种算法对TE过程进行故障诊断，将其诊断结果作为贝叶斯网络证据节点。把贝叶斯网络的故障诊断结果与采用了单一的概率神经网络诊断法和支持向量机诊断法的结果进行比较，以检验本文提出的故障诊断方案的实际效果。具体步骤如下。

①进行TE过程仿真。仿真5组数据(1组正常数据，4组加入故障的数据)，每组运行时间为48 h，采样周期为3 min，每次运行产生数据960个。其中第2～5组仿真在无故障情况下开始，并在仿真时间8 h(第160 个数据点)时分别引入故障1、2、4、9，生成5 组数据备用。

② 利用PNN和SVM算法分别对故障1、2、4、9进行诊断。从2～5组数据中分别取800个训练数据来建立PNN网络和SVM模型，再分别取测试数据各120个(第20个数据点时引入故障)来对建立的PNN网络和SVM模型进行诊断，诊断结果即为PNN和SVM算法分别对故障1、2、4、9 的诊断率。PNN 算法对故障1、2、4、9的诊断率分别为 52%、73.4%、86.6%、67.5%，SVM 算法对故障 1、2、4、9 的诊断率分别为 66.6%、90.8%、93%、83.3%。这两种算法对TE过程故障诊断效果并不十分理想。

③结合故障征兆和故障原因分析，选择与故障相关的状态变量作为贝叶斯网络节点，建立的贝叶斯网络如图4所示。

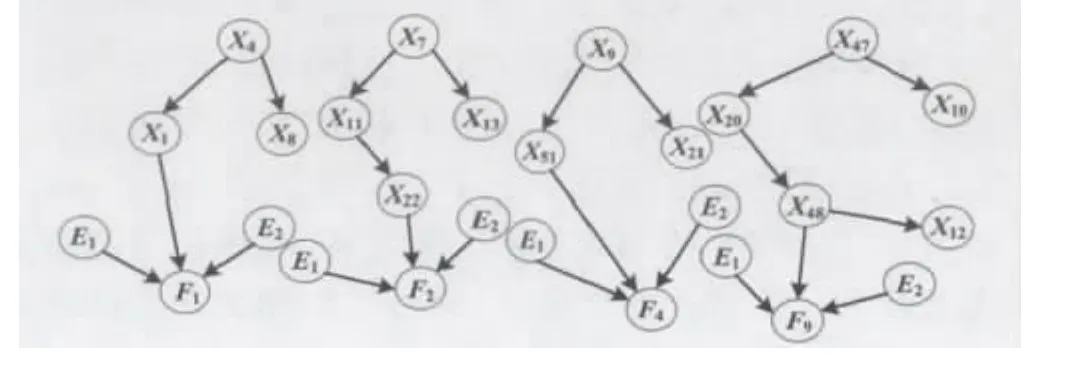
图4 改进贝叶斯网络结构图Fig.4 Improved Bayesian network structure

图 4 中，节点 X1、X4、X7、X8、X9等为状态节点，其有向边表示了各个节点相互关联，条件概率则表示相连节点之间的关联强度;节点E1和E2分别表示PNN算法和SVM算法对TE过程中4个故障诊断的证据节点;节点F1、F2、F3、F4分别对应4 种离散二值故障节点。

分别取步骤②中的测试数据进行贝叶斯参数学习，同时分别对4种故障进行贝叶斯网络推理。推理时把已知PNN和SVM算法分别对故障1、2、4、9的诊断率作为证据，推理出故障发生的概率。

改进贝叶斯网络与PNN和SVM诊断算法对故障1的诊断对比图如图5所示。其中，PNN算法和SVM算法的无故障诊断结果分别用0.3和0.25表示，PNN算法和SVM算法的有故障诊断结果则分别用0.8和0.75表示。而在BN方法下，判断各采样点故障发生的概率值从0到1分布。

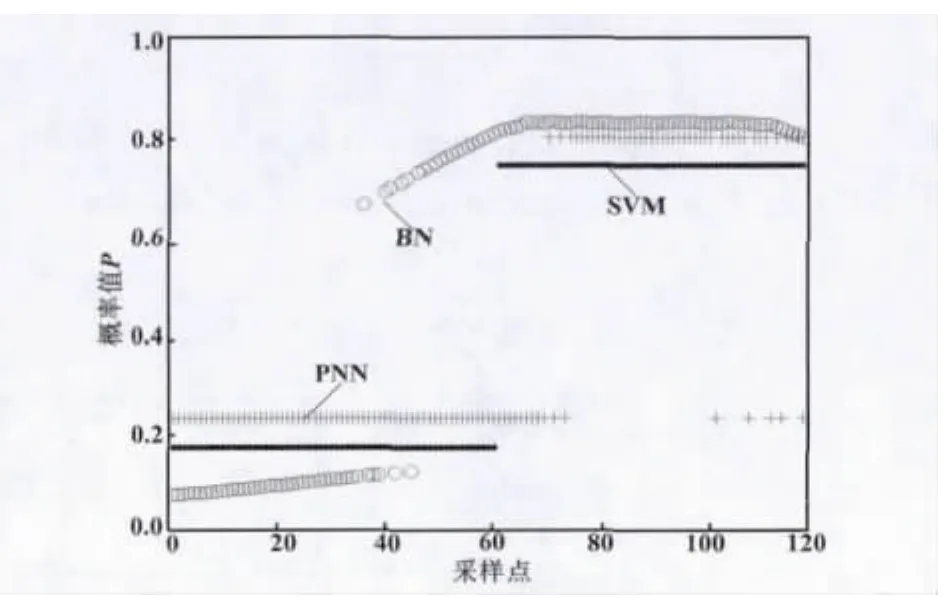
图5 故障1诊断图Fig.5 Fault 1 diagnosis

由图5可以看出，当在第20个采样点加入故障后，BN方法最快检测到故障1发生并持续到第120个采样点，且发生概率均在80%左右，可以判断故障1发生。而PNN和SVM算法对于故障1直到第60～70个采样点才检测出，并且PNN在第100至120采样点有误判的情况。

改进贝叶斯网络与PNN和SVM诊断算法对故障4的诊断对比图如图6所示。其中，PNN算法和SVM算法的无故障诊断结果分别用0.3和0.25表示，PNN算法和SVM算法的有故障诊断结果则分别用0.8和0.75表示。而在BN方法下，判断各采样点故障发生的概率值从0到1分布。由图6可以看出，当在第20个采样点加入故障后，BN方法最快检测到故障4发生并持续到第120个采样点，且发生概率均在80%左右，可以判断故障4发生。而PNN和SVM算法对于故障4相对BN方法的诊断效果要差，第21～120个采样点之间均有误判的情况。

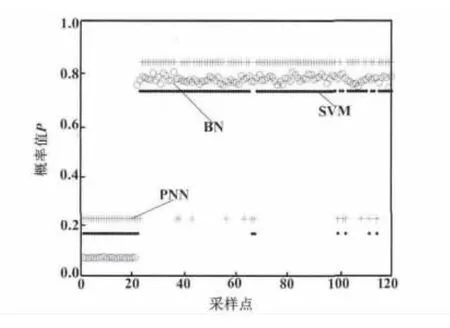
图6 故障4诊断图Fig.6 Fault 4 diagnosis

最后，本文分别计算贝叶斯网络与PNN和SVM诊断算法对故障1，2，4，9的诊断率，对比值如表2所示。由表2可以看出，贝叶斯网络方法的诊断率相对于单一的PNN和SVM有了很大提高。

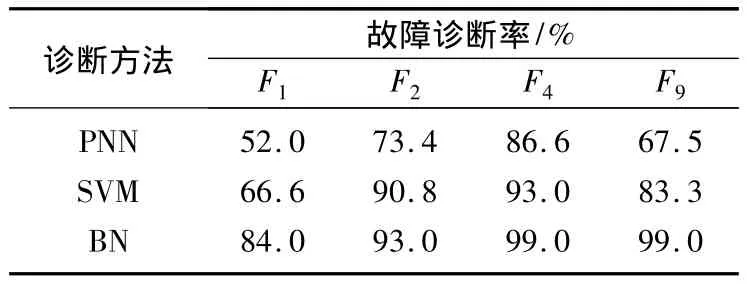
表2 故障诊断率对比表Tab.2 Comparison table of the fault diagnosis rates

4 结束语

贝叶斯网络在实现多元信息的有机融合方面具有很大的优势。本文提出的基于贝叶斯网络的故障诊断方案，把多种故障诊断方法集成到贝叶斯网络推理中，有助于全面准确地诊断复杂过程可能发生的系统故障。本文介绍了用于故障诊断的贝叶斯网络的建立和实施过程，包括单一故障诊断方法作为证据节点的添加、网络的参数学习和推理方法。采用概率神经网络和支持向量机方法对TE过程进行故障诊断方法的对比仿真，验证了所提出方法的有效性。

［1］Jelali M.An overview of control performance assessment technology and industrial applications［J］.Control Engineering Practice，2006(14):441－466.

［2］Frisk E，Nielsen L.Robust residual generation for diagnosis including a reference model for residual behavior［J］.Automatica，2006(42):437－445.

［3］Shao C X，Zhang J T.Fault diagnose base on integration of qualitative and quantitative knowledge［J］.Computer Engineering.2006，32(6):189－192.

［4］Raheem K F，Roy A，Ramachandran K P，et al.Application of the laplace wavelet combined with ANN for rolling bearing fault diagnosis［J］.Journal of Vibration and Acoustics，2008，130(5):60 －68.

［5］Verron S，Tiplica T，Kobi A.Fault detection and identification with a new feature selection based on mutual information［J］.Journal of Process Control，2008，18(5):479 －490.

［6］Straub D，Der K A.Bayesian network enhanced with structural reliability methods:methodology［J］.Journal of Engineering Mechanics，2010，136(10):1248－58.

［7］Straub D，Der K A.Bayesian network enhanced with structural reliability methods:application［J］.Journal of Engineering Mechanics，2010，136(10):1259－70.

［8］Biedermann A，Taroni F.Implementing statistical learning methods through bayesian networks.part 1:a guide to bayesian parameter estimation using forensic science data［J］.Forensic Science International，2009，193(1 －3):63 －71.

［9］Madsen A L，Jensen F V.A junction tree inference algorithm based on lazy evaluation［C］∥The Proceeding of the Fourteenth Conference on Uncertainty in Artificial Intelligence，1998:362 －369.

［10］Downs J J，Vogel F E.A plant-wide industrial process control problem［J］.Computers and Chemical Engineering，1993，17(3):245 －255.

［11］Lyman P R，Georgakisc.Plant-wide control of the tennessee problem［J］.Computer and Chemical Engineering，1995(19):321 －331.

［12］薄翠梅，李俊，陆爱晶，等.基于核函数和概率神经网络的TE过程监控研究［C］∥第二十六届中国控制会议，2007:511－515.

［13］Kulkarni A，Jayaraman K V，Kulkarni D B.Knowledge incorporated support vector machines to detect faults in Tennessee Eastman process［J］.Computer and Chemical Engineering，2005，29(10):2128－2133.