加速度计信号的小波形态滤波与样本熵分析

陈雪冬 陈硕红 徐 伟

(中国工程物理研究院电子工程研究所1，四川 绵阳 621000;西南科技大学信息工程学院2，四川 绵阳 621000)

0 引言

石英挠性加速度计是惯性导航系统的关键部件，其测量精度对整个系统的精度有着至关重要的影响。在应用过程中，加速度计不可避免地受到复杂噪声的影响。为了提高石英挠性加速度计的测量精度，对其输出信号进行降噪处理显得尤为重要。

目前，加速度信号噪声研究主要涉及数字低通滤波［1］、卡尔曼滤波［2－3］和小波阈值降噪［4－6］等。其中，数字低通滤波对非线性噪声的抑制能力不够;卡尔曼滤波需要对待处理信号建立精确的数学模型;小波阈值降噪对脉冲噪声的抑制效果较差。此外，小波域中值滤波［5］、小波卡尔曼滤波［6］等混合滤波法也用于加速度信号的降噪处理，并取得了较好的效果。

1 原理与方法

1.1 小波分析

小波分析可同时在时域和频域对信号进行多分辨分析，能有效地区分信号中的噪声和突变部分，适用于去除信号噪声［7］。对于石英挠性加速度计，其测量信号可描述为噪声的加性叠加过程，即:

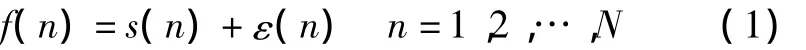
式中:N为信号的长度;s(n)为有用信号;ε(n)为噪声信号。

由于小波变换是线性的，对f(n)作离散小波变换后，获得的小波系数包含有用信号的小波系数以及噪声信号的小波系数，且有用信号的小波变换系数要大于噪声的小波变换系数［9］。选择合适的系数阈值就可实现信号与噪声的有效分离，即大于该阈值的小波系数是由有用信号引起的，小于该阈值的小波系数是由噪声引起的。阈值的选取对信号消噪的效果和重构的失真程度有着直接的影响。

小波基的选择由加速度信号的统计特性决定，选择的小波基应满足给定区间的紧支撑性和具有足够的消失距。小波分解的尺度应适中，尺度过小则不能有效地去除噪声，尺度过大则可能将有用信号去除且增大计算量。结合石英挠性加速度计信号特点，拟采用‘db6’作为小波母函数，小波分解尺度的选择由不同测试条件下加速度信号的具体特性决定。小波分解后，保留低频系数，对各个尺度的高频系数进行软阈值处理，进而对处理后的小波系数进行重构，以获取噪声抑制信号。

1.2 数学形态学

形态滤波器是一种建立在集合理论基础上的非线性滤波器［10］，能有效地提取信号的边缘轮廓和信号的形状特征，其基本运算包括膨胀和腐蚀等。

令输入序列f(n)为定义在F={0，1，…，N －1}上的离散函数，离散结构元素g(n)的定义域为G={0，1，…，M －1}，且 N≥M。那么，f(n)关于 g(n)的腐蚀和膨胀表达式分别如式(2)、式(3)所示。

膨胀运算是一种扩张变换，能除去信号的负脉冲并平滑正脉冲;腐蚀运算是一种收缩变换，能去除信号的正脉冲并平滑负脉冲。

使用彩色多普勒超声造影模式，通过超声造影剂声诺维5毫升生理盐水，将其溶解后为其抽取2.4毫升。后期使用10毫升的生理盐水冲洗，并对产妇的子宫螺旋动脉和胎儿结局详细研究。

结合腐蚀和膨胀操作，关于f(n)的形态开运算和形态闭运算分别定义为:

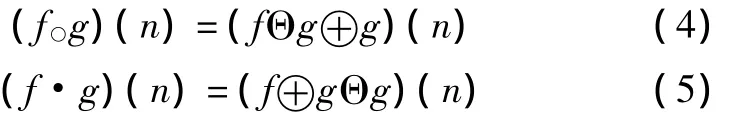
形态开运算可以抑制信号波峰噪声，闭运算则可抑制信号波谷噪声［11］。为了同时去除信号中的正、负脉冲噪声，可采用开、闭运算级联形式，定义形态开-闭(OC)和闭-开(CO)运算［12－13］，即:

将这两种运算进行组合平均，以提高滤波效果，即:

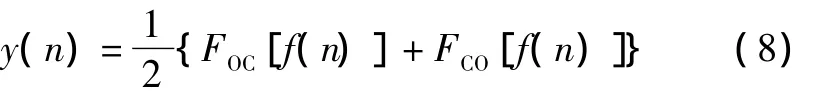
结构元素在形态滤波中的作用类似于一般信号处理中的滤波窗口，其形状和大小影响着加速度信号的降噪效果。结构元素的选取主要取决于待处理信号的形态，应尽可能类似于待处理信号的图形特点［11］。结合石英挠性加速度信号及测试过程，本文选择三角形作为结构元素。确定结构元素的形状后，应选择合适的幅值和宽度，使滤波效果达到最佳。就三角形结构元素而言，幅值一般取原始波形高度的1% ～5%最适宜［14］。形态滤波的使用主要是为了消除加速度信号中的脉冲干扰，所以结构元素的宽度应小于待测信号的长度，并大于干扰脉冲的宽度。

1.3 样本熵

样本熵(sample entropy，SE)是一种度量序列复杂度的测试方法，可用来定量描述复杂系统的不确定性［15］。噪声的存在会引起加速度信号的不确定性，且噪声干扰越严重，加速度信号的不确定性越大，其样本熵也越大;相反，噪声干扰越弱加速度信号的不确定性越小，其样本熵也越小。因此，可采用样本熵对加速度信号的降噪效果进行评价分析。

对于N个数据x(1)，…，x(N)，可将其组成一组形如 Xm(i)=［x(i)，x(i+1)，…，x(i+m －1)］的 m维向量，其中，1≤i≤N－m+1，这些向量表示从第i点开始的m个连续的x的值。向量Xm(i)与Xm(j)的距离为两者对应元素中最大绝对差值［16－18］，即:

对于给定的 Xm(i)，统计 d［Xm(i)，Xm(j)］≤r的数目(1≤j≤N － m，j≠i)，并记作 Bi，可得:

增加维数到(m+1)，再次统计最大绝对差值不大于r的数目，可得到Bm+1(r)，则样本熵的计算可描述为［19－20］:

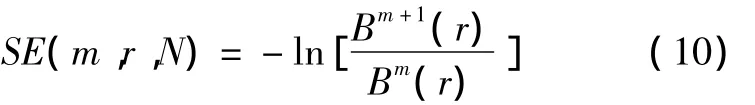
样本熵与相似容限r、维数m的取值有关，它由具体加速度信号的特点决定。一般情况下，取r=0.1～0.25STD(STD为原始信号的标准差)，m=2。

2 试验与分析

为验证所采用方法的有效性，分别对重力场和离心机两种条件进行试验测试。其中，测量信号由具有16位分辨率的采集卡PCI-6221获得，采样率设置为1000 Hz。对采集的加速度信号进行小波阈值降噪和形态滤波，采用样本熵与统计参数对降噪的效果进行分析评价。

2.1 重力场测试数据分析

重力场测试时，利用夹具将石英挠性加速度计固定在多齿分度台上，进行多点翻滚试验，采集石英挠性加速度计位于不同角度时的输出信号。以0°时的加速度信号为例进行降噪分析。

取1 s的0°加速度信号进行降噪处理，小波降噪时尺度设置为3，形态滤波的结构元素采用幅值相同但尺度不同的三角形。降噪结果如图1所示。

图1 信号降噪前后对比图Fig.1 Comparison of signals before and after noise reduction

降噪前后加速度信号的评价参数如表1所示。

表1 评价参数统计表Tab.1 Statistics of the evaluation parameters

从表1可以看出，信号样本熵与统计标准差得到明显降低，而统计均值基本保持不变，表明取得了良好的降噪效果。

为进一步验证样本熵的降噪评价效果，采用10 s数据进行统计分析，且以1 s数据作为一个分析段。对每个分析段进行降噪处理，获得加速度信号降噪前后的样本熵与统计参数分布图如图2、图3所示。从图2、图3可以看出，随着降噪算法的改进，加速度信号的样本熵逐渐减小，表明了由噪声引起的不确定性受到了明显的抑制，信号中的噪声逐渐减少;统计参数的变化趋势也反映了信号中的噪声逐渐减小且信号的稳定性逐渐增强，从而验证了样本熵具有良好的降噪评价效果。

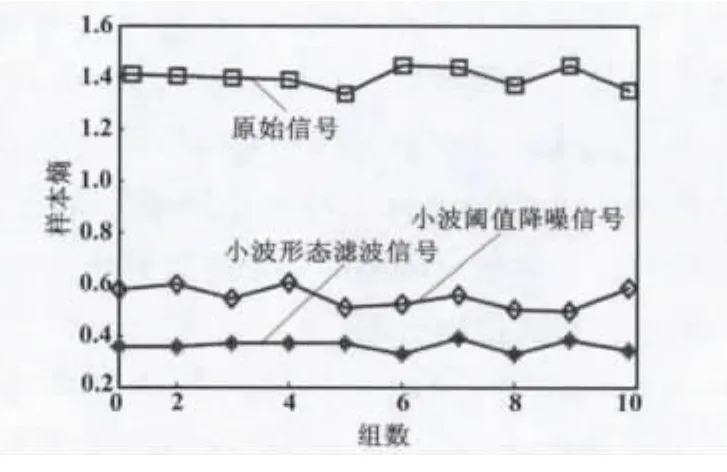
图2 重力场加速度信号降噪前后样本熵分布图Fig.2 Distribution of sample entropy of acceleration signals

图3 重力场加速信号降噪前后统计参数分布图Fig.3 Distribution of statistical parameters of acceleration signals

结合0°加速度信号的降噪结果以及评价参数统计分析，利用小波形态滤波法能够有效地去除信号中的噪声成分;同时，采用信号分段降噪分析的方式，进一步验证了所采用降噪方法对信号的较好适应性。

由以上试验分析可知，小波形态滤波法可获得较好的降噪效果，且样本熵能对降噪效果进行有效评价。重力场静态测试时，石英挠性加速度计所处的测试环境相对稳定，采用本文降噪方法同样能有效地去除其他角度下的加速度信号噪声。

2.2 离心机测试数据分析

离心机动态测试是将石英挠性加速度计安装在离心机上，采集处于不同加速度值(0～75g，g为当地的重力加速度值)时的输出信号，且测量信号会受到噪声干扰。以70g时加速度信号为例进行降噪分析，采用与分析重力场加速度信号类似的分析方法。离心机加速度信号降噪前后的对比图如图4所示。

图4 离心机加速度信号降噪前后对比图Fig.4 Comparison of the centrifugal acceleration signals before and after noise reduction

离心机降噪前后信号的特征统计如表2所示。

表2 离心机加速信号降噪前后的评价参数统计表Tab.2 Statistics of the evaluation parameters for the centrifugal acceleration signals before and after noise reduction

加速度信号降噪前后样本熵分布图与统计参数分布图分别如图5、图6所示。

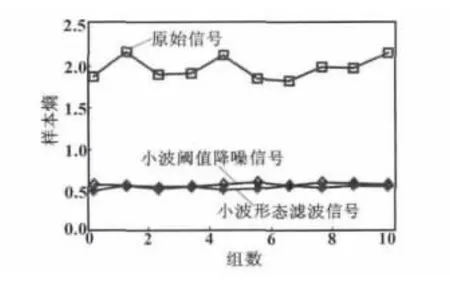
图5 离心机加速度信号降噪前后样本熵分布图Fig.5 Distribution of the sample entropy of the centrifugal acceleration signals before and after noise reduction

图6 离心机加速度信号降噪前后统计参数分布图Fig.6 Distribution of the statistical parameters of the centrifugal acceleration signals before and after noise reduction

3 结束语

为了提高石英挠性加速度计的测量精度，本文采用融合小波分析与数学形态学的方法对加速度信号进行降噪处理，并采用了样本熵与统计参数对降噪效果进行评价。通过对重力场静态测试和离心机动态测试时的加速度信号进行降噪分析可知，所采用的方法能有效地去除加速度信号中的噪声，同时较好地保留了原始信号的主要特征，且样本熵对降噪效果具有较好的描述性。

［1］陈江良，陆志东.基于Matlab的数字滤波器设计及其在捷联惯导系统中的应用［J］.中国惯性技术学报，2005，13(6):10 －12.

［2］马跃，李松，李莹，等.加速度计信号处理的建模与仿真［J］.计算机仿真，2012，29(3):351 －354.

［3］Kownacki C.Optimization approach to adapt Kalman filters for the real-time application of accelerometer and gyroscope signal’s filtering［J］.Digital Signal Processing，2011，21(1):131 －140.

［4］徐超，沈晓蓉，李建军，等.车载微加速度计信号的去噪技术研究［J］.传感器技术学报，2007，20(11):2442 －2444.

［5］Wu P，Ge Y S，Chen S T，et al.De-noising algorithm based on compression of wavelet coefficient for MEMS accelerometer signal［C］//Proceeding of the 2010 IEEE International Conference on Information and Automation，Harbin，China:402－407.

［6］胡柏青，魏峥，王伯雄，等.强噪条件下基于小波降噪的陀螺仪声信号处理方法［J］.传感技术学报，2008，21(6):1007 －1009.

［7］滕军，朱焰煌，周峰，等.自适应分解层数的小波域中值滤波振动信号降噪法［J］.振动与冲击，2009，28(12):58 －62.

［8］覃方君，许江宁，李安，等.基于小波卡尔曼滤波的加速度计降噪方法［J］.武汉理工大学学报:理工版，2009，33(1):49 －52.

［9］曾守帧.小波去噪及其在信号处理中的应用［D］.天津:天津大学，2007.

［10］Serra J.Morphological filtering:an overview［J］.Signal Processing，1994，38(1):3 －11.

［11］郝如江，卢文秀，诸福磊.形态滤波在滚动轴承故障发射信号处理中的应用［J］.清华大学学报:自然科学版，2008，48(5):812 －815.

［12］Maragos P，Schafer R W.Morphological filters-partⅠ:their set-theoretic analysis and relation to linear shift invariant filters［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1987，35(8):1153－1169.

［13］Maragos P，Schafer R W.Morphological filters-part II:their relations to median，order-statistic，and stack filters［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1987，35(8):1170 －1184.

［14］胡爱军，唐贵基，安连锁.振动信号采集中剔除脉冲的新方法［J］.振动与冲击，2006，25(1):126 －128.

［15］赵志宏，杨绍普.一种基于样本熵的轴承故障诊断方法［J］.振动与冲击，2012，31(1):136 －141.

［16］Pan Y H，Wang Y H，Liang S F，et al.Fast computation of sample entropy and approximate entropy in biomedicine［J］.Computer Methods and Programs in Biomedicine，2010，104(2011):382 －396.

［17］Angari H M，Sahakian A V.Use of sample entropy approach to study heart rate variability in obstructive sleep apnea syndrome［J］.IEEE Transactions on Biomedical Engineering，2007，54(10):1900 －1904.

［18］Alcaraz R，Rieta J J.A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms［J］.Biomedical Signal Processing and Control，2010，5(1):1 －14.

［19］Lake D E，Richman J S，Griffin M P，et al.Sample entropy analysis of neonatal heart rate variability［J］.Physiology Regulatory Integrative and Comparative Physiology，2002，283(3):789 －797.

［20］Angari H，Sahakian A.Use of sample entropy approach to study heart rate variability in obstructive sleep apnea syndrome［J］.IEEE Transactions on Biomedical Engineering，2007，54(10):1900 －1904.