大口径舰炮供弹系统变幅同步摆机构分析

2014-05-31叶小红李少远姜贵林王茂林王洪光

应用科技 2014年2期

叶小红，李少远，姜贵林，王茂林，王洪光

哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001

射速是火炮系统的一个主要性能指标，而供弹速率在一定程度上限制了火炮的发射速率［1］。单发发射的时间主要包括摆臂下摆接弹上摆送弹时间、输弹时间、关闩时间、瞄准时间、击发时间、后坐回复时间，先瞄准后供弹的斜式供弹方式通过将瞄准时间与摆臂摆弹时间同时进行而节省了供弹时间，提高供弹速率［2］。这样的斜式供弹方式为了保证摆臂确实上摆至发射角同轴线，引入了一个变幅同步问题，即随着射角的变化，摆臂上摆摆角也将发生相应的变化以保证同轴输弹供弹［3］。

现有的火炮系统多采用自动化的控制手段，虽然原理简单，却也存在液压系统调整困难、不稳定，缓冲器(既要缓冲又要保证充分到位)不可靠，动力源难以统一等缺点［4］。但是机械式变幅同步摆机构是摇架与摆臂之间的一个机械装置，用于实现摇架与摆臂的同步［5］，从而实现了射角与摆臂摆角同步的目的，不存在上面问题，运动可靠。

俄式76 mm舰炮的装填摆是典型的机械式变幅同步摆，现以此摆为例进行同步摆运动分析，作为新同步摆设计分析的参考。

1 斜式装填的射角与摆角关系

供弹方式中的斜式装填是指在炮弹进入炮膛之前先行进行瞄准，调整摇架的俯仰角——射角，而后摆臂上摆至膛线位置并到位，所以为了在不同射角状态下都能保证供弹到位，摆臂需要实时的变换摆角来适应不同的射角。于是在假定摆臂和摇架的初始位置分别是垂直位置和水平位置的条件下，摆角α和射角φ之间关系式［6］为:

图1所示是舰炮供弹系统同步机构的摆角与射角的原理关系图。射角φ定义为膛线与水平线的夹角，摆臂摆角α定义为膛线与铅垂线的夹角。

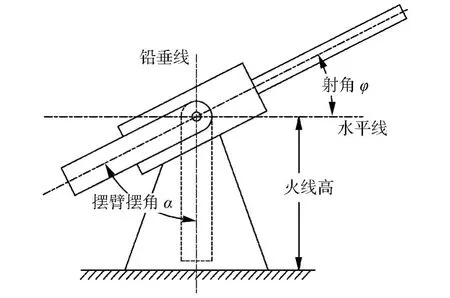
图1 同步机构的摆臂与射角关系图

2 变幅同步摆机构的工作原理

变幅同步摆机构的原理图如图2所示，主要包括了两部分:摆臂驱动传动部分和摇架同步自适应部分。

摇架同步自适应部分主要包括了摇架上的曲线槽2，三角形杠杆12以及滑块10，摇架以耳轴O1为转动中心，三角形杠杆旋转中心O2固定在炮架上。当摇架调整射角时，摇架以O1为中心转动，三角形杠杆12通过连杆带动滑块10移动到位，变心D是随着滑块移动的。

图2 变幅同步摆机构

摆臂驱动传动部分是由曲柄7驱动，滑块5的移动使滑槽连杆8沿着变心D发生移动和转动，从而由后续的传动机构带动齿弧齿条机构，最终带动摆臂转动一定角度。于是可以通过精确计算曲线槽的形状来控制滑块10的移动，从而保证变心D的不同位置实现摇架1转动一定的射角位置时，摆臂必定上摆到射角同轴线位置，实现同步［7］。

3 机构简化与分析

为了方便分析，这里将完整的变幅同步摆机构模型进行分解和简化，由动点D分开，拆成两部分:摆臂驱动传动部分和摇架自适应部分，分别对2个模型进行自由度计算和位置分析，并在最后将2个系统进行耦合，从而得到凸轮曲线槽曲线方程。

3.1 机构模型分解及自由度计算

3.1.1 机构模型分解与简化

将图2简化拆成如图3和图4所示的2个机构，各含有一个驱动。图3是摆臂驱动，由曲柄的转动带动终端齿条的移动(因为齿轮对整个机构的运动分析没有影响，所以这里先将齿轮略去)，令D点固定;图4是摇架驱动，摇架沿耳轴的转动相当于是凸轮的转动，带动D点移动，此处D点为移动点。

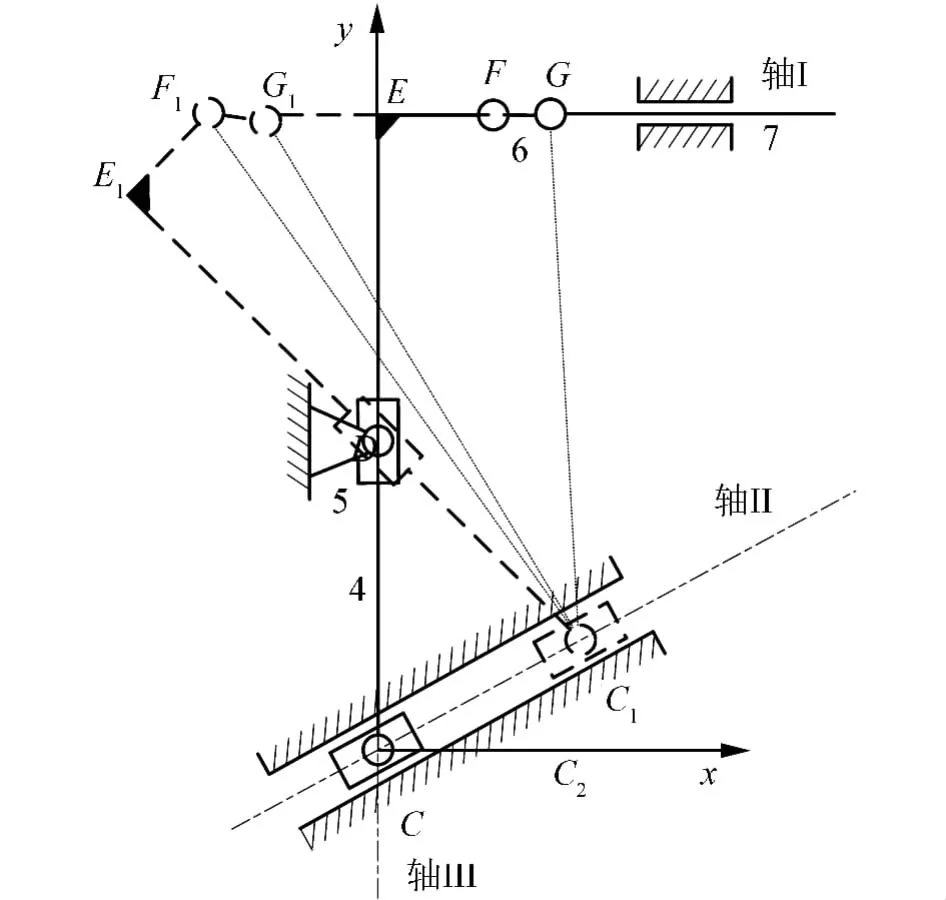
图3 摆臂驱动机构

图4 摇架自适应机构

其中有3处固定轴线位置，齿条移动方向固定，AC方向固定，动点D的移动方向固定，且其位置关系设为已知［8］。

3.1.2 模型的自由度计算

平面机构自由度与机构中活动构件的数目、低副数目和高副数目有关，其计算公式如下:式中:n是机构中可动构件的数目，pl是低副数目，ph是高副数目［9］。

于是分别对图2、3、4进行自由度计算，得:

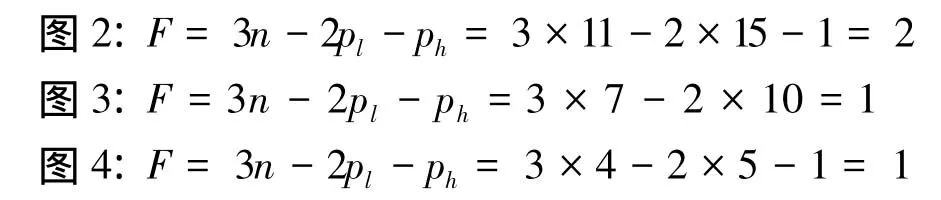
显然，分解前后机构都有确定的运动状态。

3.2 机构初始位置分析

3.2.1 摆臂驱动机构初始位置分析

如图3所示的实线部分和虚线部分分别是摆臂驱动机构的2个极限位置，其中实线位置时摆臂处于初始位置，当变换到虚线位置时，摆臂也由初始位置摆动到膛线位置。

为了保证不同的射角情况下，动点D的位置变化不会对摆臂机构初始位置产生影响，使摆臂每次都是从垂直位置上摆，本机构使连杆4的初始轴线位置与动点D的导轨方向重合，从而保证无论动点D怎么移动都不会影响到摆臂驱动机构［10］。

且在初始位置时，点C即是滑块3的初始点，同时也是滑块5的导轨轴线与滑块3的导轨轴线的焦点，且当滑块3处于C点时，点E、F、G实现3点共线。

3.2.2 摆臂驱动机构初始位置分析

如图4所示，实线部分为摇架自适应机构，为了分析方便，只取其中连杆部分进行分析，初始位置时，射角为0°，动点D处于D0位置，当射角为 φ时，动点由D0移动到D。

3.3 机构位置分析

由于本机构的摆臂有7°的折角，所以需对摆角与射角的关系式(1)修改为

3.3.1 摆臂驱动机构的位置分析

如图3所示的摆臂机构，已知各杆件的长度为li(i=1，2，4，5) 和 EF=b，导向 I、II和 III固定，并如图建立坐标系，则有 C( 0 ，0)、D( 0 ，yD) 、E( 0 ，l4)、F( b ，l4) 和 G( b +l5，l4)确定的位置关系，且根据齿条位移G1G与摆臂转角α的关系式可有G1G=Rα，其中R是耳轴中心到齿条的垂直距离，由三角关系和坐标关系可有

于是ΔCC1D中，已知得到了

根据三角形正弦定理有

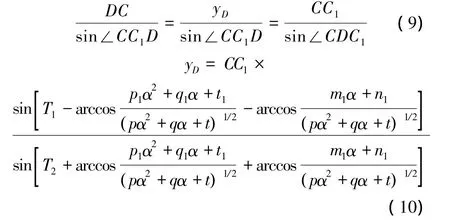
式(10)是经过常数简化后的yD关于α的显式表达式，并简写为yD=f( α)，方便后面的计算。

3.3.2 摇架自适应机构的位置分析

设图4机构的初始位置已知，由图建立坐标系，即已知 ∠HO2O=β ，∠IO2H，D( 0 ，yD) ，D0(0 ，yD)和O1( xO1，yO1)，并设∠H1O2H=θ，则有

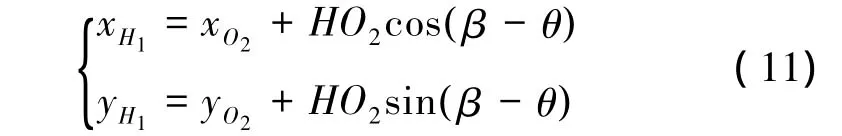
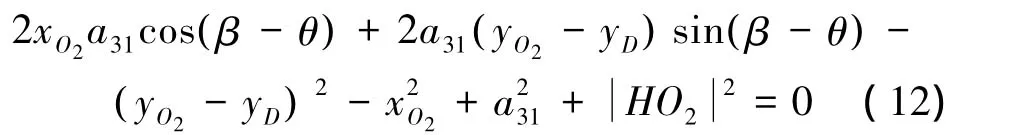
由三角计算公式可得

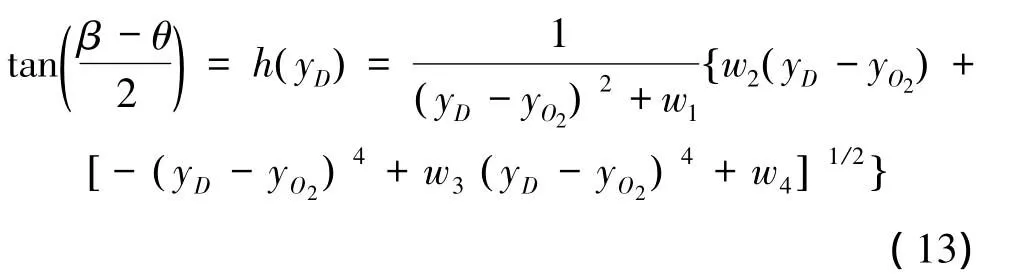
由上式可以求得θ=β－2arctan A，其中A是关

用关于 yD的函数 g yD( )代替式(14)中的2arctan A－∠IO2H，从而将I1的坐标简写成于yD的函数。从而可以得到I1的坐标为

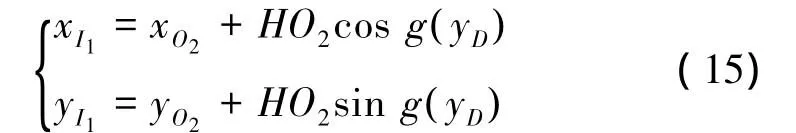
3.3.3 凸轮曲线槽分析

图5中，曲线槽是固定在摇架上，当摇架以O1点为轴心转动φ(即射角为φ)时，曲线槽也以O1点为轴心转动φ，即曲线槽在固定坐标系C-xy中的位置也发生变化，而点I1在摇架上的位置和在固定坐标系中的位置均发生变化，为了得到曲线槽的各点在摇架上的对应位置，首先需求得当摇架处于初始位置时，长度 IO1关于射角 φ的坐标表达式以及∠I1O1O。

图5 曲线槽形状分析

结合等式(3)和(10)，得到yD关于φ的显式表达式yD=(f 97°－φ )，并最终得到连杆端点I1关于α的坐标表达式为

设已知耳轴位置点O1的坐标为 ( xO1，yO1)，所以可以计算得 |I1O1|的长度如下:

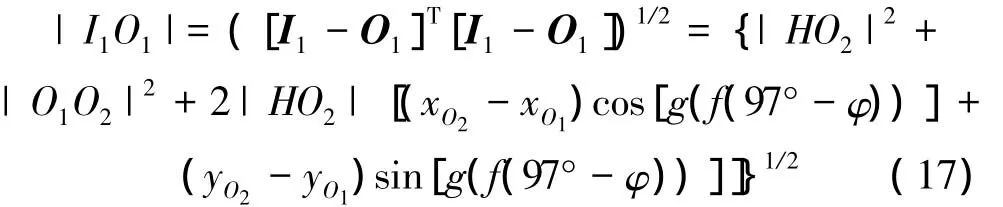
简化式(17)中的常数，并设ρ= | IO1|，则 ρ的表达式为

点I1和点 O1的连线 I1O1与水平线的夹角∠I1O1O可以在该两点已知的状态下求得如下:

简化常数可得

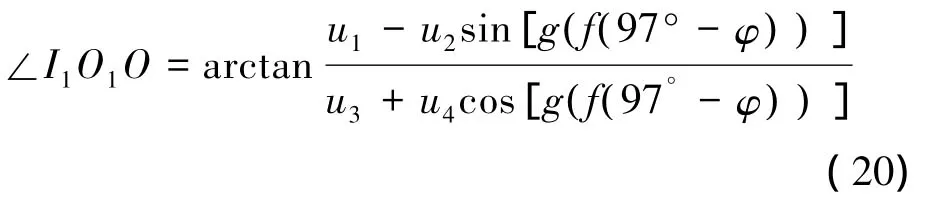
由图5可知，曲线槽相对于摇架的角度 φ=∠I1O1O－φ，则最终可得到曲线槽曲线的极轴坐标方程为

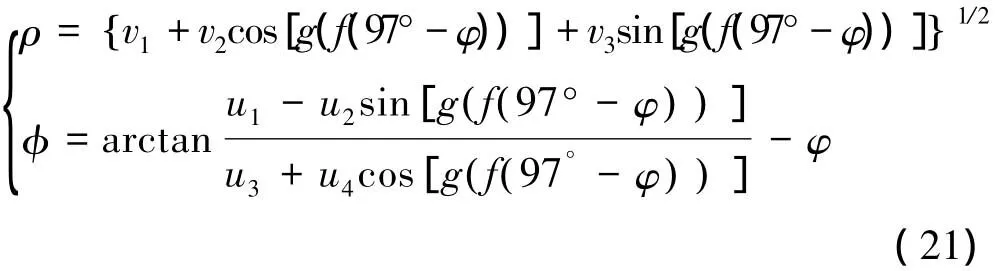
由上式可知，曲线槽的位置和形状均由唯一参数射角φ确定，当φ取值－15°～85°时可得到一系列的连续点，从而得到了凸轮曲线，整个的变幅同步摆机构的设计与位置分析也完成了。

3.4 摆臂始末速度分析

摆臂的始端是一个曲柄滑块机构，而对于曲柄滑块机构的速度和加速度分析已经非常成熟，也直接引用现有的研究成果［11］。

从图2中可知，本机构是一个正置曲柄滑块机构，在假定曲柄输入为恒定的情况下，假定曲柄与CC1逆时针角度为σ，可以视滑块的近似速度为

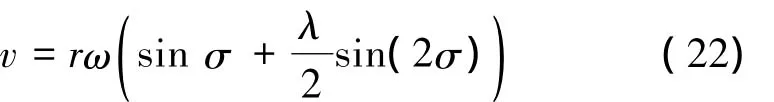
式中:r为图2中杆7的长度，λ是杆件7和6的长度比，可将滑块的近似速度曲线绘制如图6所示。

图6 滑块速度曲线

当σ∈0，π[)的过程中，曲柄从初始位置出发并达到极限位置，而该过程中滑块的速度为由0变到vmax，再由vmax减小到0，从而保证摆臂在上摆送弹过程中速度没有跃变，并在摆弹上摆到位时理论上没有冲击。当σ∈π，2π[)的过程中，曲柄从极限位置回到初始位置，该过程中滑块的速度由0变到－vmax，再由vmax减小到0，即保证摆臂在下摆接弹过程中速度没有跃变，从而实现摆臂起始提速和摆弹下摆到位时理论上没有冲击。而这是控制系统所不能完成的。