基于高速供弹过程的杆式穿甲弹冲击力仿真分析

2021-12-20欧阳稠焦延博郑添春王均涛

火炮发射与控制学报 2021年4期

欧阳稠，焦延博，郑添春，王均涛

(宜春先锋军工机械有限公司，江西宜春 336000)

供弹机是舰炮自动供弹机构的重要组成部分，起到弹药定位和输弹入膛的作用，它在很大程度上决定了整个武器系统的可靠性[1]。对于小口径防空火炮的供弹弹鼓，当高速供弹时导引肋板与杆式穿甲弹之间的冲击将对穿甲弹的结构产生一定影响，进而对其内弹道、外弹道以及毁伤效能造成一定的影响。国内学者对舰炮弹鼓和弹链等供弹机构展开了研究[2-5]，王钢等针对弹鼓储弹和单线扬弹过程，分析了动力学特性[6]。笔者主要讨论高速供弹过程中导引肋板与杆式穿甲弹之间的冲击问题，对供弹机进行运动学分析，并利用LS-DYNA显式动力有限元仿真软件对高速供弹过程中导引肋板与杆式穿甲弹之间以及杆式穿甲弹各零部件之间的冲击过程进行数值仿真，分析供弹过程中冲击对杆式穿甲弹结构及力学性能的影响，为生产和实弹连射试验提供参考。

1 数值分析

供弹系统主要有直线供弹和转动供弹两种供弹模式。直线供弹模式主要采用链轮的旋转带动链条作直线运动，肋板带动杆式穿甲弹随链条同时运动[7]。转动供弹模式是由拨弹轮旋转拨动杆式穿甲弹作圆周运动，现对以上两种供弹模式进行运动学分析。对于供弹结构，系统的坐标矢量组可表示为

(1)

式中：qi为供弹构件i的坐标矢量；n为供弹系统中的构件个数，归一化约束处理后供弹结构系统欧拉参数矢量方程组为[8]

(2)

供弹系统的运动学约束矢量方程组为

(3)

式中，m为供弹系统中运动约束的个数。

令约束方程

ΦD(q,t)=0，

(4)

可得到

(5)

求导可得构件速度方程:

(6)

由于式(6)不包含时间t变量，则有

(7)

对式(6)进一步求导得到加速度方程:

(8)

对于横向冲击过程初始运动条件，可设火炮射频为f(转管自动炮在转动过程中连续完成循环射击运动，最理想的供弹过程为匀速供弹，此时拨弹机构受到的冲击力最小，运动可靠性最高)，导引肋板的节距为l，拨弹轮半径为r。忽略杆式穿甲弹在火炮中运动的时间，弹丸与弹链视为固连，炮弹与拨弹轮和肋板均为接触碰撞，则供弹肋板的平均移动速度和拨弹轮角速度计算如下，并有：

v=l·f,

(9)

ω=x×v.

(10)

设导引肋板之间的距离为52 mm，系统供弹速率为5 000发/min。供弹模式运动参数计算结果如表1所示。将以上条件作为仿真模型初始条件进行加载。

表1 供弹过程运动参数

横向冲击过程采用碰撞函数来描述，冲击力Fx表示为

(11)

式中：e为非直线系数；c为阻尼系数，取刚度系数的0.1%～1%；d为形变深度；x为相互作用构件的距离变量；x0为两构件碰撞初始距离；k为惩罚函数，即刚度系数，根据Hertz接触理论有

(12)

式中：R为零部件接触位置处的曲率半径；E为零部件材料的弹性模量。

2 仿真模型

在高速供弹过程中，杆式穿甲弹将受到导引肋板对整弹的冲击，若此横向冲击过大，将导致整弹的零部件结构发生塑性变形。因此，现对杆式穿甲弹和导引肋板进行结构有限元仿真，分析供弹过程中杆式穿甲弹整弹内部的应力分布。在高速供弹过程中存在转动供弹与直线供弹两种供弹模式，由于两种供弹模式的系统结构复杂，国内外学者多采用ADAMS对供弹系统进行仿真[9-10]，而杆式穿甲弹整弹在供弹过程中横向冲击对杆式穿甲弹零部件结构力学性能的影响程度是笔者所关注的。因此，将两种供弹模式简化为转动导引肋板与直线导引肋板进行研究并作如下假设[11]：

1)穿甲弹零部件的变形在弹性范围内，不考虑材料的非线性项；

2)求解过程中，肋板作为刚体进行处理；

3)药筒的变形完全是由肋板与药筒的过盈配合引起的，不考虑其他力引起的药筒变形。

对于杆式穿甲弹建模，考虑到仿真模型结构的复杂性，忽略对整弹影响较小的尼龙弹带和橡胶闭气环结构，以便简化仿真模型，提高仿真计算速度。杆式穿甲弹有限元模型中，尾翼采用四面体网格，网格大小为1.0 mm，风帽、整弹采用六面体网格，网格大小为1.0 mm，弹托、药筒采用扫略网格，网格大小为1.0 mm，导引肋板采用扫略网格，主体部分网格大小为1.2 mm，与药筒接触部分网格大小为1.0 mm。

设定杆式穿甲弹各零部件之间采TIED_NODES_TO_SURFACE接触，导引肋板与药筒之间采用AUTOMATIC_SINGLE_SURFACE接触，导引肋板定义径向恒定的运动速度，以模拟导引肋板对整弹的冲击作用[12-13]。

对两种导引肋板分别建模，转动导引肋板和直线供弹节有限元仿真模型分别如图1(a)和图1(b)所示，转动供弹、直线供弹和杆式穿甲弹有限元仿真模型分别如图1(c)～(e)所示。

非金属零部件，如尼龙弹带和橡胶闭气环等不在本文中分析，仿真模型中相关材料参数如表2所示。

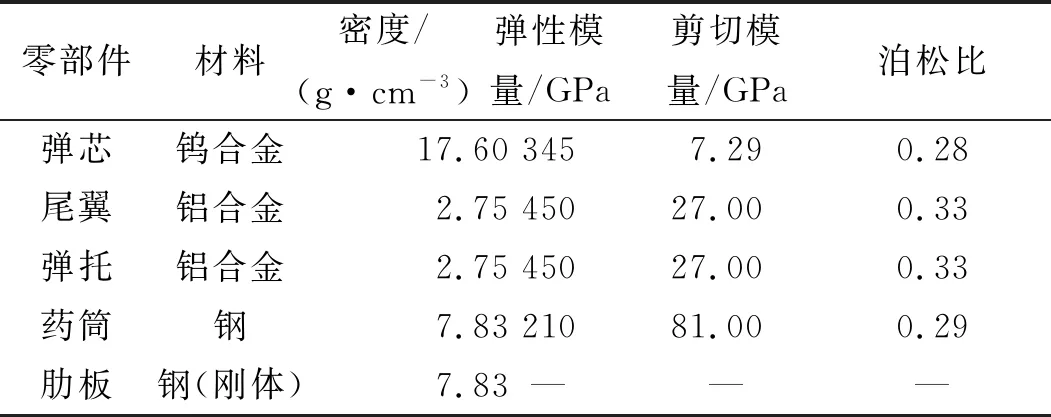
表2 仿真模型中相关材料参数

3 仿真结果

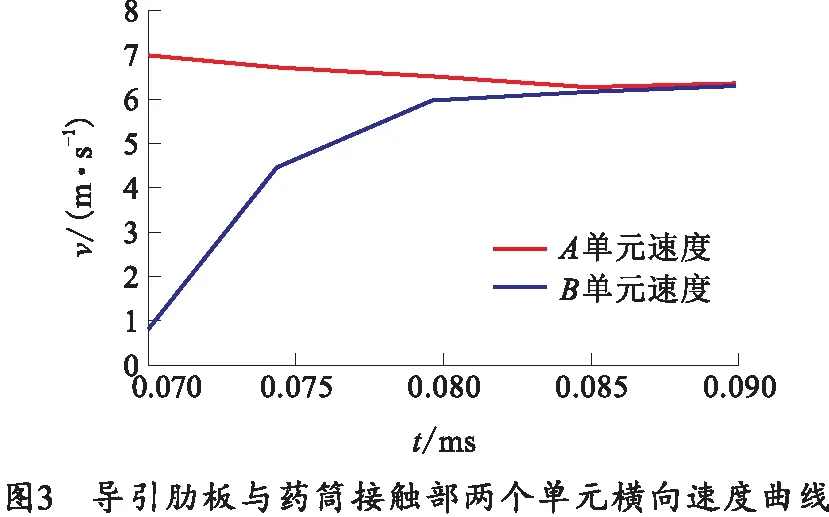
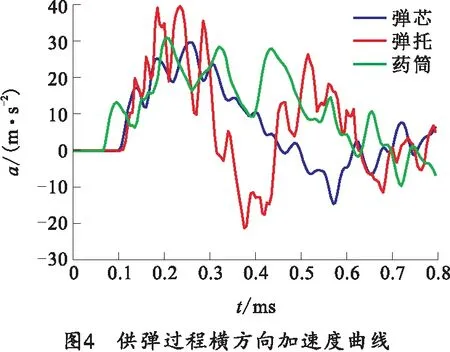
在转动供弹过程中，取导引肋板与药筒上接触部分上两个单元A和B，所取单元位置如图2所示。导引肋板与杆式穿甲弹碰撞过程横方向速度曲线如图3所示，该过程为强制输弹过程，穿甲弹受到导引肋板作用开始加速，在t=0.085 ms时穿甲弹和导引肋板的速度相等，此后两者速度保持接近，可知，此阶段两者完成碰撞后一起运动，供弹横向冲击过程结束，进入稳定供弹阶段，直线供弹模式采用相同方式判断横向冲击结束时刻。整弹零部件结构加速度曲线如图4所示。

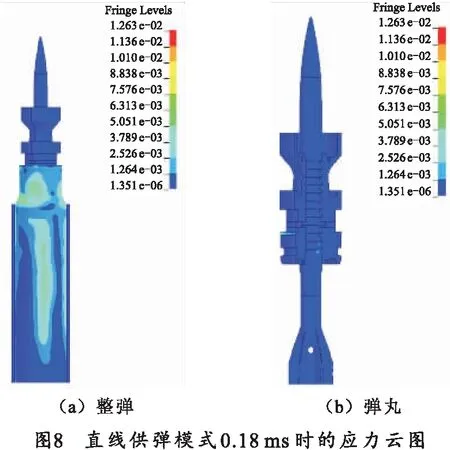
利用LS-DYNA求解器对仿真模型进行数值模拟，对整弹应力云图进行处理，转动供弹模式的应力云图如图5、6所示，直线供弹模式的应力云图如图7、8所示。

在后处理模式中，为了分析杆式穿甲弹各零部件结构中关键位置应力情况，在仿真模型中设置相应的等效应力观察点，观察点具体位置如图9所示。其中观察点A位于导引肋板接触位置(同图2所示位置)，B位于药筒与供弹链肋板接触位置附近(同图2所示位置)，C位于弹托周向位置处，D、E、F、G分别沿弹芯自上而下分布，等效应力随时间变化曲线如图10所示。观察点处的分析处理结果如表3所示。

表3 观察点处的分析处理结果

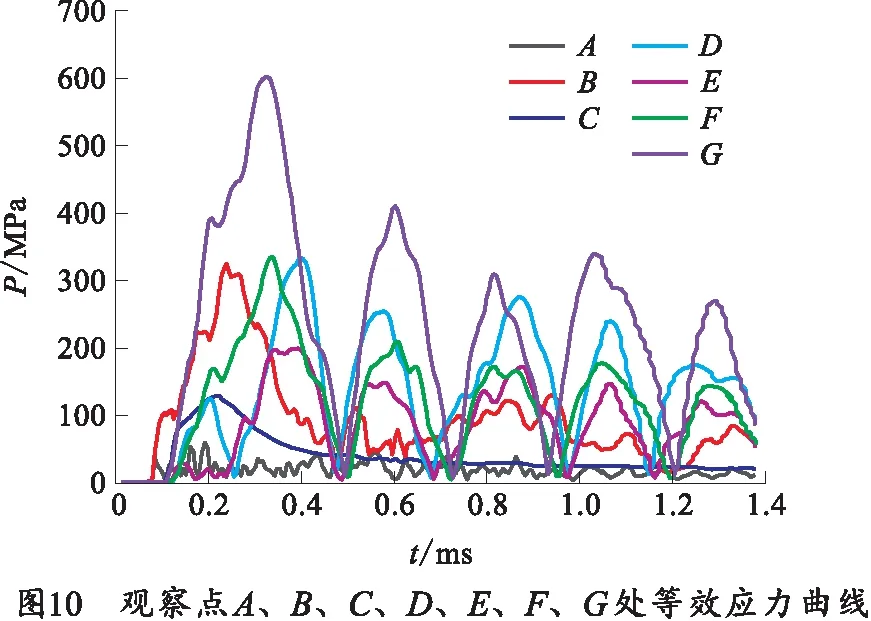
由仿真结果可以看出：在转动供弹模式中整弹在受到导引肋板的冲击作用过程中，弹芯4个自上而下观察点最大应力峰值依次为332，199，334，604 MPa，应力最大值位于下部G点；弹托应力峰值为132 MPa；药筒应力峰值为327 MPa，药筒安全系数最小。对于弹芯，由于钨合金材料抗压不抗剪，在横向冲击模式，应力集中位置极易产生微小裂纹，影响其力学性能。在直线供弹模式中，弹芯4个自上而下观察点最大应力峰值依次为62，103，134，207 MPa，应力最大值位于下部G点；弹托应力峰值为198 MPa；药筒应力峰值为500 MPa，药筒安全系数最小。