高斯噪声背景下多用户波达方向估计与互耦自校正

景小荣 杨 洋 张祖凡 陈前斌



高斯噪声背景下多用户波达方向估计与互耦自校正

景小荣①②杨 洋*①张祖凡①②陈前斌①②

①(重庆邮电大学通信与信息工程学院 重庆 400065)②(移动通信技术重庆市重点实验室 重庆 400065)

在高斯噪声背景下，针对互耦条件下的均匀线阵(Uniform Linear Array, ULA)，该文提出了一种联合多用户波达方向(Direction Of Arrival, DOA)估计与互耦误差自校正算法。该算法首先利用特征矩阵联合相似对角化(Joint Approximative Diagonalization of Eigen matrix, JADE)方法估计出各用户广义空间特征矢量，然后定义了一个将各用户广义空间特征矢量转换为只与部分阵元相关的转换矩阵，进而在斜投影及前后向空间平滑的基础上，实现了多用户相干信源DOA估计，最后以多用户相干信源DOA及广义空间特征矢量估计值为基础，给出一种互耦自校正方法。仿真结果表明：该算法具有较高的DOA估计精度及DOA估计成功率，而且对高斯白噪声/色噪声背景，阵列互耦误差已知/未知情形，均具有普适性。

信号处理；多用户DOA估计；均匀线阵；互耦自校正

1 引言

高分辨测向技术广泛地应用于雷达、声呐及无线通信领域，目前已涌现出许多性能优良的DOA估计算法，其中以多重信号分类(MUltiple SIgnal Classification, MUSIC)算法[1]及基于旋转不变技术的信号参数估计(Estimating Signal Parameters via Rotational Invariance Techniques, ESPRIT)算法[2]最为经典。然而，这两种算法均基于理想阵列流形提出。在实际应用中，受阵元间互耦影响，实际阵列流形与理想阵列流形之间总存在一定偏差，导致这些算法DOA估计性能急剧下降，甚至失效。

为了解决互耦条件下DOA估计问题，国内外学者进行了深入研究。文献[3]将互耦条件下的DOA估计转化为多维非线性优化问题，并利用多步迭代法求解，然而，无法保证迭代收敛性。Wang等人[4]则利用互耦矩阵(Mutual Coupling Matrix, MCM)的Toeplitz结构，提出一种DOA估计与互耦自校正方法。文献[5]利用稀疏分解的方法，实现了互耦条件下的DOA估计问题。Liao等人[6]将互耦误差转换成与角度相关的复阵列增益，提出了一种DOA与互耦误差联合估计算法。文献[7]基于改进稀疏分解算法，实现了信源DOA估计。Wang[8]基于最大似然(Maximum Likelihood, ML)准则，利用辅助校正源的空域与时域波形信息来实现DOA与互耦/幅相误差的联合估计。这些研究成果均针对非相干信源。

在实际无线通信中，同一用户信号经过障碍物时，会造成反射，从而形成多径信号，当多径时延差较小时，通常认为这些多径信号是相干的，即形成相干信源。相干信源的存在使得上述DOA估计算法不再适用。为此，Dai等人[9]提出利用改进空间平滑算法解相干，进而实现互耦条件下相干信源DOA估计。文献[10]中提出两种解相干算法，用以解决互耦条件下相干信源的DOA估计问题。

以上文献，均假设高斯白噪声环境，且只利用了接收数据的二阶统计量信息。而在移动蜂窝通信系统中，受小区外多址干扰(Out-cell Multiple Access Interference, OMAI)的影响，将通信背景噪声建模为高斯色噪声显得更为合理。同时，相比二阶统计量，四阶累积量(Fourth-Order Cumlants, FOC)具有更好的信号表征特性，同时又具有盲高斯性及虚拟阵列孔径扩展的能力。Li等人[11]基于FOC，研究了互耦条件下独立信源的DOA估计问题，然而，文中算法对相干信源DOA估计仍然无能为力。更为重要的是，在实际移动通信环境中，与基站间同时通信的终端用户往往不止一个。为此，在多用户通信场景(或存在多组相干信源时)，Gonen等人[12]提出了一种虚拟ESPRIT算法(Virtual ESPRIT Algorithm, VESPA)，用以解决多用户相干信源DOA估计问题；Cardoso等人[13]则提出JADE方法，用于解决多用户相干信源盲波束形成问题，但是，这些方法均不适用阵元间存在互耦误差的情形。

综合分析以上成果，本文针对均匀线阵(ULA)互耦条件下多用户DOA估计的难点，提出了一种联合DOA估计与互耦自校正算法。与VESPA算法相比，该算法不但在DOA估计精度及DOA估计成功率上，具有明显的优势，而且对于高斯白/色噪声背景，阵列互耦误差已知/未知情形，均具有普适性。

2 信号模型

3 高斯噪声背景下多用户DOA估计与互耦自校正

3.1 多用户DOA估计与互耦自校正

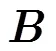
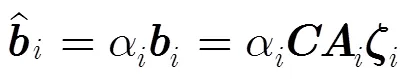
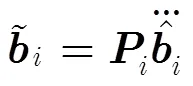
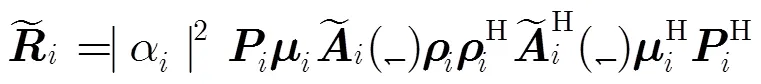
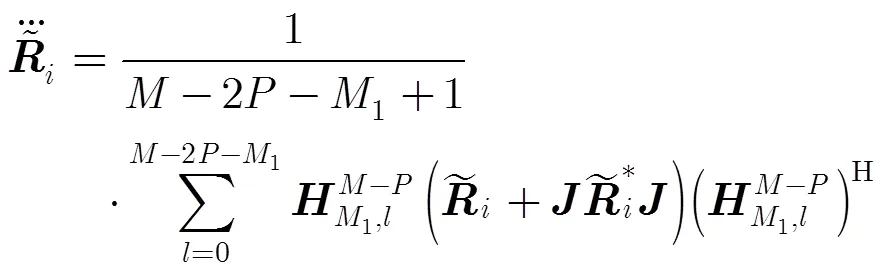
3.2 互耦系数矢量估计

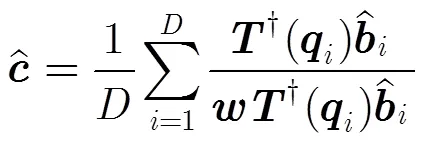
4 数值仿真实验

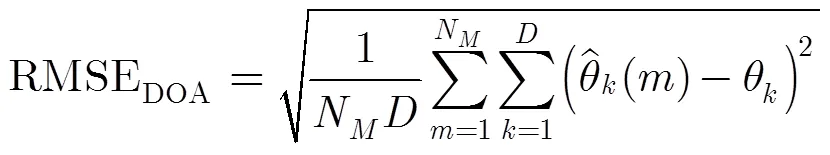
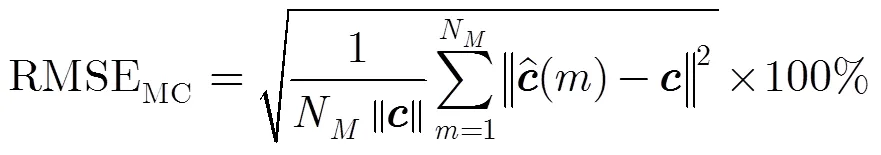
图1 空间功率谱

图2 随SNR变化曲线

图3 随SNR变化的关系曲线

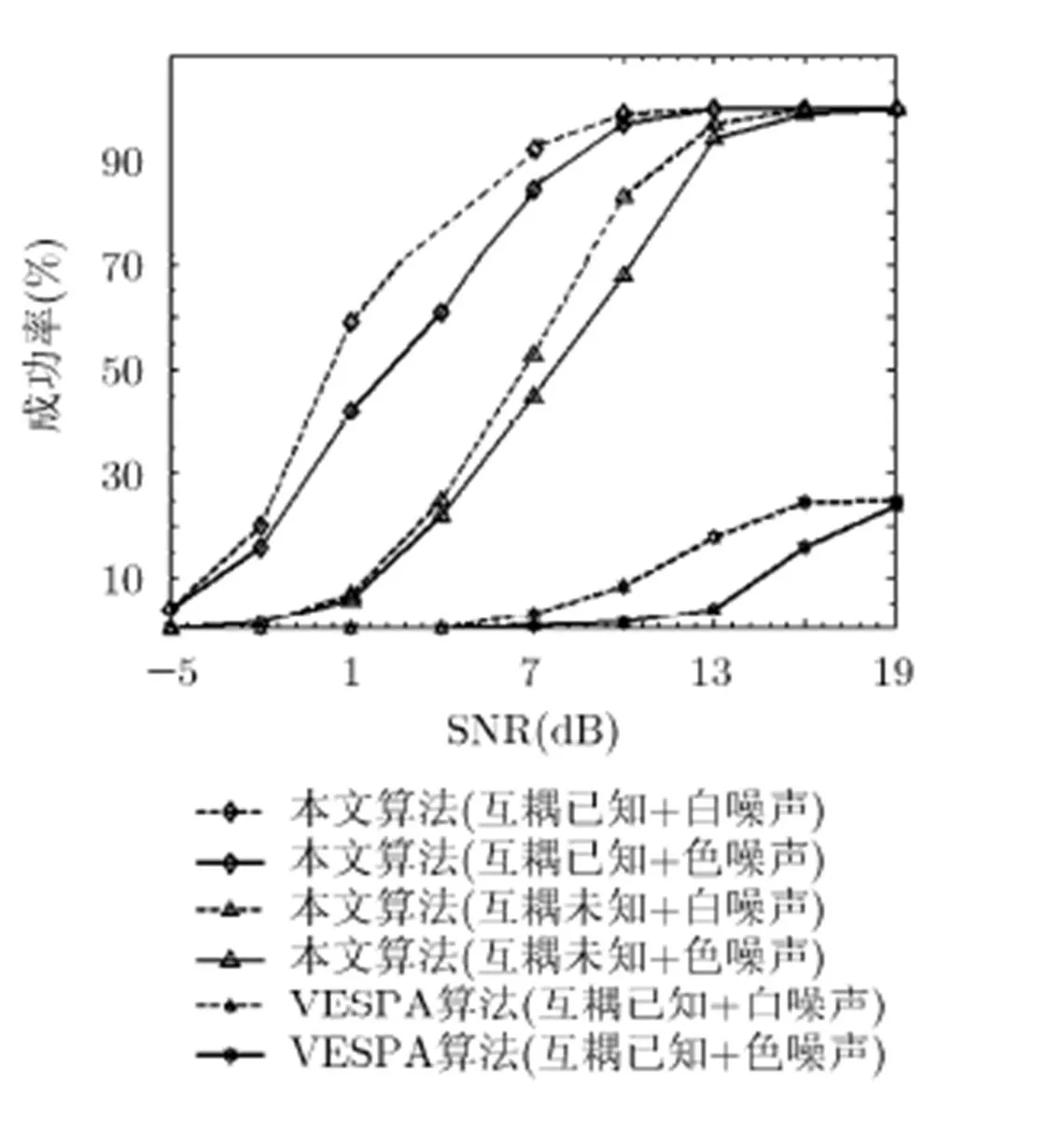
图4 DOA估计成功率随SNR变化的曲线

5 结束语

高斯噪声环境下，本文针对ULA互耦条件下多用户DOA估计及互耦误差校正问题，结合JADE方法，提出了一种联合DOA估计与互耦误差自校正算法。该算法不仅可以有效地实现多用户DOA估计，还能够自动对来波按用户进行分组；与VESPA算法相比，该算法无论从DOA估计精度及DOA估计成功率，均具有明显的优势，而且对于互耦已知及未知情形，以及高斯背景噪声均具有普适性；同时，算法在实现DOA估计的基础上，还可精确地估计出互耦系数矢量，从而实现阵列的自校正。此外，由于本文算法利用JADE方法来估计广义空间特征矩阵，且采用斜投影来消除多用户间干扰，因此，算法复杂度相对较高，然而，随着微处理器运算能力的提升，该问题会逐步得到解决。

[1] Schmidt R O. Multiple emitter location and signal parameter estimation[J]., 1986, 34(3): 276-280.

[2] Roy R H and Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J].,, 1989, 37(7): 984-995.

[3] Friedlander B and Weiss A J. Direction finding in the presence of mutual coupling[J]., 1991, 39(3): 273-284.

[4] Wang B H, Wang Y L, Chen H,.. Robust DOA estimation and array calibration in the presence of mutual coupling for uniform linear array[J].., 2004, 47(3): 348-361.

[5] Wang L B and Chen C. Direction-of-arrival estimation in the presence of mutual coupling based on joint sparse recovery[J].(), 2012, 29(5): 408-414.

[6] Liao B, Zhang Z G, and Chan S C. DOA estimation and tracking of ULAs with mutual coupling[J]., 2012, 48(1): 891-905.

[7] Dai J S, Zhao D A, and Ji X F. A sparse representation method for DOA estimation with unknown mutual coupling [J]., 2012, 11: 1210-1213.

[8] Wang D. Sensor array calibration in presence of mutual coupling and gain/phase errors by combining the spatial- domain and time-domain waveform information of the calibration sources[J]., 2013, 32(3): 1257-1292.

[9] Dai J S and Ye Z F. Spatial smoothing for direction of arrivalestimation of coherent signals in the presence of unknownmutual coupling[J]., 2011, 5(4): 418-425.

[10] Liao B and Chan S C. DOA estimation of coherent signals for uniform linear arrays with mutual coupling[C]. 2011 IEEE International Symposium on Circuits and Systems (ISCAS),Hong Kong, 2011: 377-380.

[11] Li X, Ye Z F, Xu X,.. Direction of arrival estimation for uniform circular array based on fourth-order cumulants in the presence of unknown mutual coupling[J]., 2008, 2(3): 281-287.

[13] Cardoso J F and Souloumiac A. Blind beamforming for non-Gaussian signals[J]., 1993, 140(6): 362-370.

[14] Dou H, Li G P, and Shi J C. A fast algorithm for DOA estimation based on fourth-order cumulants[J]., 2012, 127(4): 61-67.

[15] Behrens R T and Scharf L L. Signal processing applications of oblique projection operators[J]., 1994, 42(6): 1413-1424.

景小荣： 男，1974年生，副教授，博士，研究方向为多天线(包括智能天线)系统中的信号处理.

杨 洋： 男，1987年生，硕士生，研究方向为智能天线系统信号处理.

张祖凡： 男，1972年生，教授，博士，研究方向为移动通信网络及理论.

Multiuser DOA Estimation and Mutual Coupling Error Self-calibration in Gaussian Noise Backgrounds

Jing Xiao-rong①②Yang Yang①Zhang Zu-fan①②Chen Qian-bin①②

①(,,400065,)②(,400065,)

In the Gaussian noise background, an algorithm is proposed to jointly estimate the multiuser DOA and self-calibrate the mutual coupling error for Uniform Linear Array (ULA). First, the generalized spatial feature vector of each user is estimated by utilizing the Joint Approximative Diagonalization of Eigen (JADE) matrix method. Second a transformation matrix is defined, and based on which the generalized spatial feature vector is converted to the one which is related with part elements of the ULA. Then the multiuser coherent DOA estimates are obtained on the basis of the oblique projection and Forward and Backward Spatial Smoothing(FBSS) methods. Finally, a mutual coupling self-calibration method is presented by utilizing the estimates of the DOA and the generalized spatial feature vector of each user. The computer simulation indicates that the algorithm has higher performance of DOA estimation accuracy and successful rate. The simulation results also demonstrate that, the proposed algorithm is universal for the situations where the mutual coupling error is known or not with white or colored additive Gaussian noise.

Signal processing; Multiuser DOA estimation; Uniform linear array; Mutual coupling self-calibration

TN911.7

A

1009-5896(2014)05-1266-05

10.3724/SP.J.1146.2013.01042

杨洋 yangyme@163.com

2013-07-16收到，2013-11-07改回

国家科技重大专项(2013ZX03003008-005)和重庆市自然科学基金(CSTC, 2010BB2417, 2013JJB40001)资助课题