基于非均匀快速傅里叶变换的SAR方位向运动补偿算法

邢 涛 李 军 王冠勇 胡庆荣



基于非均匀快速傅里叶变换的SAR方位向运动补偿算法

邢 涛*①李 军②王冠勇①胡庆荣①

①(北京无线电测量研究所 北京 100854)②(西安电子科技大学雷达信号处理重点实验室 西安 710071)

沿航向的非匀速运动对SAR成像质量有很大影响，而运动补偿后SAR图像存在几何形变，影响子图像拼接和多波段SAR图像融合。当沿航向速度误差较大时，实图像域插值校正后图像残留的几何形变不能忽略。基于上述问题，该文提出一种基于非均匀傅里叶变换的SAR方位向运动补偿算法，算法直接对方位向的非均匀数据进行非均匀快速傅里叶变换(NUFFT)。该算法的定位误差和几何形变比实图像域插值校正几何形变算法小1到2个数量级，对沿航向速度误差有很强的鲁棒性，补偿后数据的幅度和相位信息都得以保留。SAR仿真和实测数据验证了该算法的有效性。

合成孔径雷达；运动补偿；几何形变校正；非均匀快速傅里叶变换

1 引言

SAR成像要求雷达天线相位中心匀速直线运动。在实际应用中，受载机本身误差和外界大气环境等多种因素制约，天线相位中心沿航向的前进速度是时变的，这种时变运动对成像质量的影响很大[1,2]，因而沿航向运动补偿是十分必要。

沿航向速度的时变导致空间采样位置的不均匀，解决办法是根据时变速度实时调节雷达重复频率使采样位置沿航向均匀分布，或者把在非均匀位置上采集到的数据插值到均匀位置上。实时调整雷达重复频率增加了设备的复杂度和成本；对数据复数插值运算量大，并且存在一定的插值误差。针对上面两种解决办法的不足，文献[3]提出了一种沿航向运动误差补偿方法，这种方法对沿航向运动误差的补偿非常有效，但是成像后图像存在几何形变。文献[4]对此方法进行了改进，通过对SAR图像插值校正几何形变。在沿航向速度误差较小时文献[4]方法可以有效地校正几何形变。而当沿航向速度误差较大时，校正后图像残留的几何形变不能忽略，这影响了大速度误差下该方法在SAR成像中的应用。另外，该方法的插值是对图像数据的幅值进行的，相位信息被舍弃。

2 NUFFT快速计算

与均匀数据离散傅里叶变换(DFT)类似，非均匀数据的离散傅里叶变换为

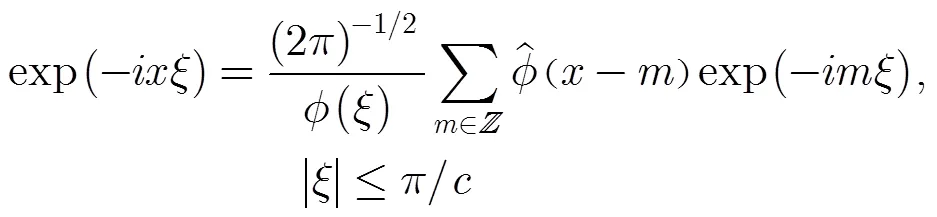
图1 NUFFT计算示意图

3 基于NUFFT的SAR方位向运动补偿算法

3.1 方位向非均匀傅里叶变换

图2 SAR方位成像目标模型

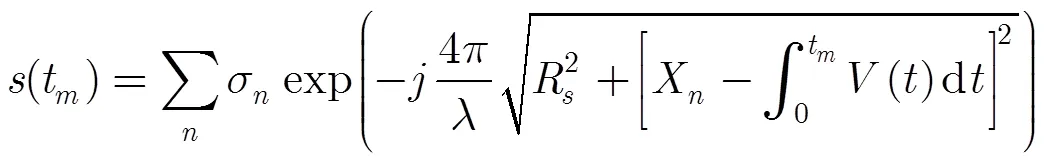
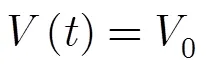
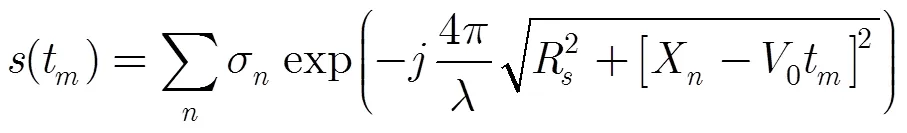
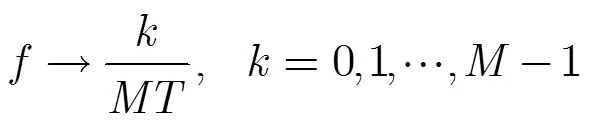
令

由式(12)，式(13)得

由式(10)，式(14)得

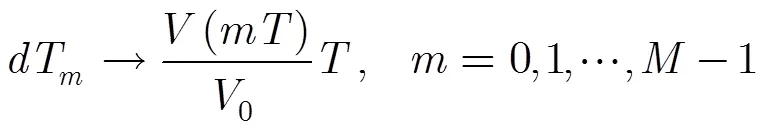
输入、输出分别对应如下：

把式(10)～式(18)代入式(9)第1个等号两边，得

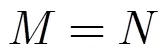
把式(20)～式(23)代入式(19)，得

式(24)等式右边和式(1)等式右边完全一样，因此，可以利用第2节NUFFT快速计算方法来计算式(19)，即得到了非均匀输入下离散化的频谱，这种频谱与沿航向匀速直线运动时的频谱(式(8)的傅里叶变换)一样。

3.2 基于NUFFT的SAR方位向运动补偿算法

从图3可知，原始脉压，CACGD, CIFFT, NUFFT成像流程中距离徙动校正、距离脉压、距离IFFT、方位脉压、方位IFFT等处理是一样的。在表1中，对这4种成像流程公共处理部分没有进行仿真，仅统计了这4种成像算法流程中各自独有的操作部分的运行时间。

图3 SAR成像算法流程

表1 算法在不同点数时200次实验的平均运行时间(ms)

4 仿真和实测数据实验

4.1 仿真结果对比

点目标仿真参数：10 GHz，脉冲重复频率2000 Hz，场景中心距离5 km，相干积累角为1o，方位分辨率1 m。设置了3个点目标，分别在-100 m,0 m, 100 m处，平台初始速度100 m/s，沿航向速度误差为高斯分布的随机变量，设置了两组速度误差：小速度误差(均值为0，标准差为3)和大速度误差(均值为20，标准差为10)。

图4(a), 4(b)为两种速度误差下4种算法在3个方位点目标处的仿真图，表2为与图4(a), 4(b)对应的数据记录。

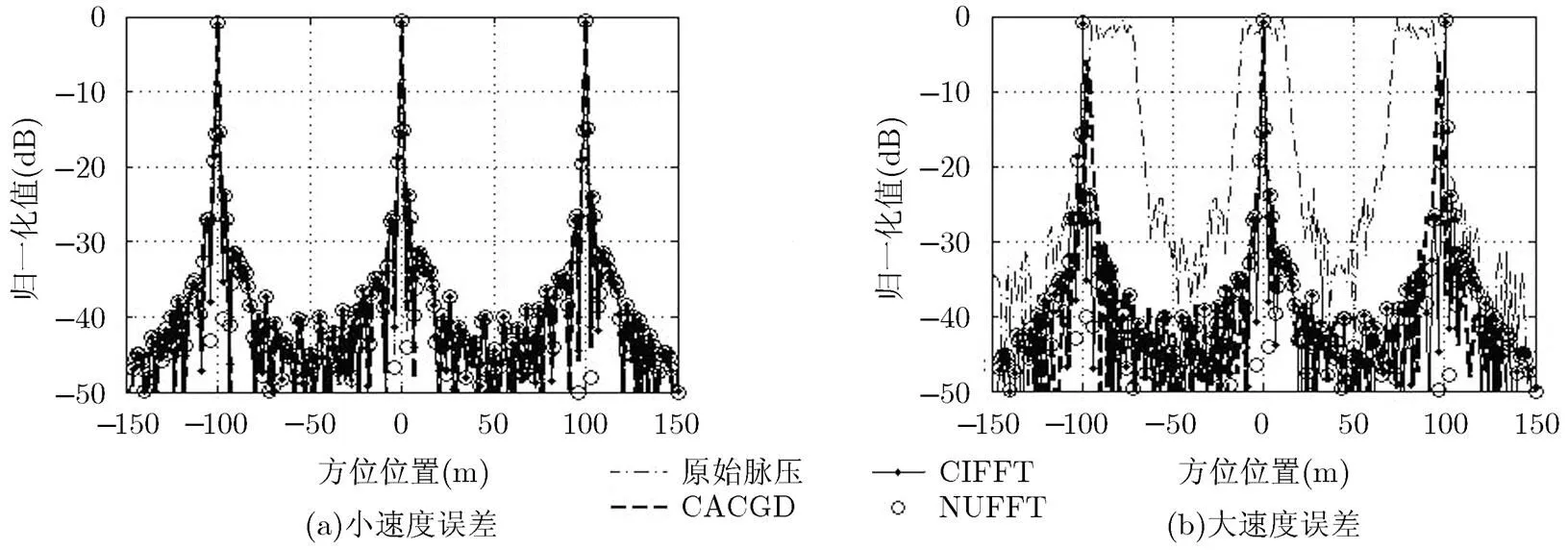
图4 点目标仿真图

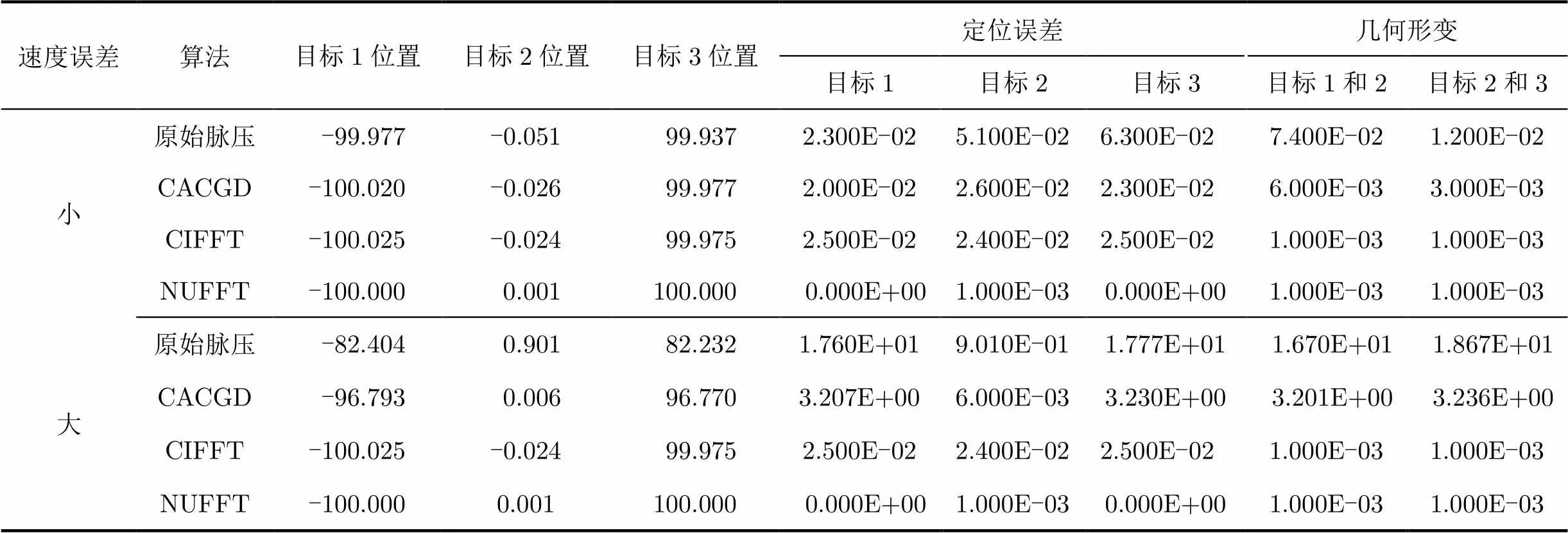
表2 不同沿航向速度误差下方位点目标仿真结果(m)

图5(a), 5(b), 5(c) 3幅图是把图4(a), 4(b)中-100 m, 0 m, 100 m处4种算法成像仿真曲线的-3 dB尖峰放大后的情形。表3为0 m处点目标在不同速度误差下的主瓣展宽系数IRWR(实际主瓣宽度/理想主瓣宽度)，峰值旁瓣比PSLR和积分旁瓣比ISLR的数据记录，仿真中没有加窗函数。

图5(a), 5(b), 5(c)和表3表明：随着速度误差的增大，原始脉压算法主瓣急剧展宽，分辨率降低；CACGD算法在某些点目标处仿真曲线的峰值低于-3 dB，有可能漏检目标，且波形发生畸变；CIFFT算法和NUFFT算法主瓣展宽系数、峰值旁瓣比和积分旁瓣比基本不随速度误差变化而变化，波形保形较好，对沿航向速度误差具有较强的鲁棒性。

4.2 实测数据结果对比

实测速度误差验证：速度由挂飞的IMU测得，不考虑IMU测量误差。记实测速度相对其初始值的变化量为实测速度误差，变化规律如图6所示，把图6的速度误差加到图7横轴所示的相应速度上作为时变的沿航向速度。图7为4种算法在-100 m, 0 m, 100 m这3个点目标处的定位误差随平台速度的变化关系。图8为沿航向速度误差按照图6变化时，4种算法几何形变随平台速度的变化关系。

图7(a), 7(b), 7(c)表明：NUFFT算法定位误差比原始脉压算法定位误差小3到4个数量级，NUFFT算法定位误差比CACGD算法和CIFFT算法定位误差小1到2个数量级。曲线的起伏大小表明：CIFFT算法和NUFFT算法对速度(即相对速度误差)的鲁棒性比较强。图8(a), 8(b)表明：NUFFT算法和CIFFT算法几何形变基本相同，几何形变量比CACGD算法要低1到2个数量级。

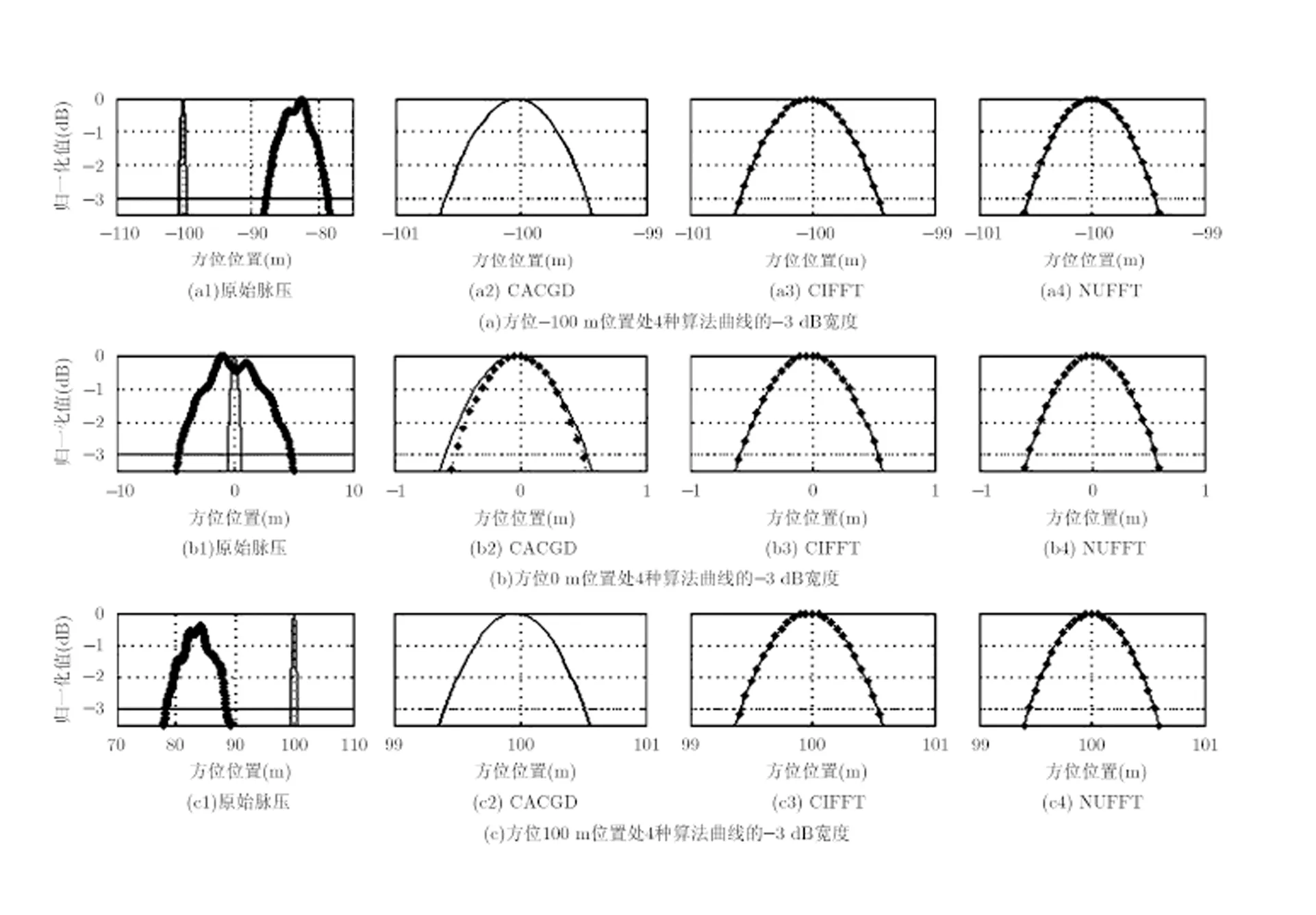
图5 点目标仿真曲线的-3 dB宽度(粗点线：大速度误差；细实线：小速度误差)

表3不同速度误差下4种算法点目标的特性比较

指标原始脉压CACGDCIFFTNUFFT 小速度误差大速度误差小速度误差大速度误差小速度误差大速度误差小速度误差大速度误差 IRWR 1.0030.81 1.00 0.93 1.00 1.00 1.00 1.00 PSLR(dB)-13.29-8.09-12.96-11.62-13.39-13.38-13.38-13.38 ISLR(dB) -9.84-9.97 -9.83 -8.74 -9.77 -9.77 -9.77 -9.77

图9表明：在存在沿航向速度误差，尤其是较大相对误差下，原始脉压算法对非均匀数据直接进行方位FFT导致SAR图像数据相位存在较大相对误差，CACGD算法只对成像数据幅值进行插值校正，相位的相对误差依然较大，CIFFT算法对原始非均匀数据进行了复数插值，图像数据某些点上相位相对误差较大，NUFFT成像算法由于其中的方位NUFFT部分以很高的精度接近式(1)直接计算值，而具有很好的保相性。

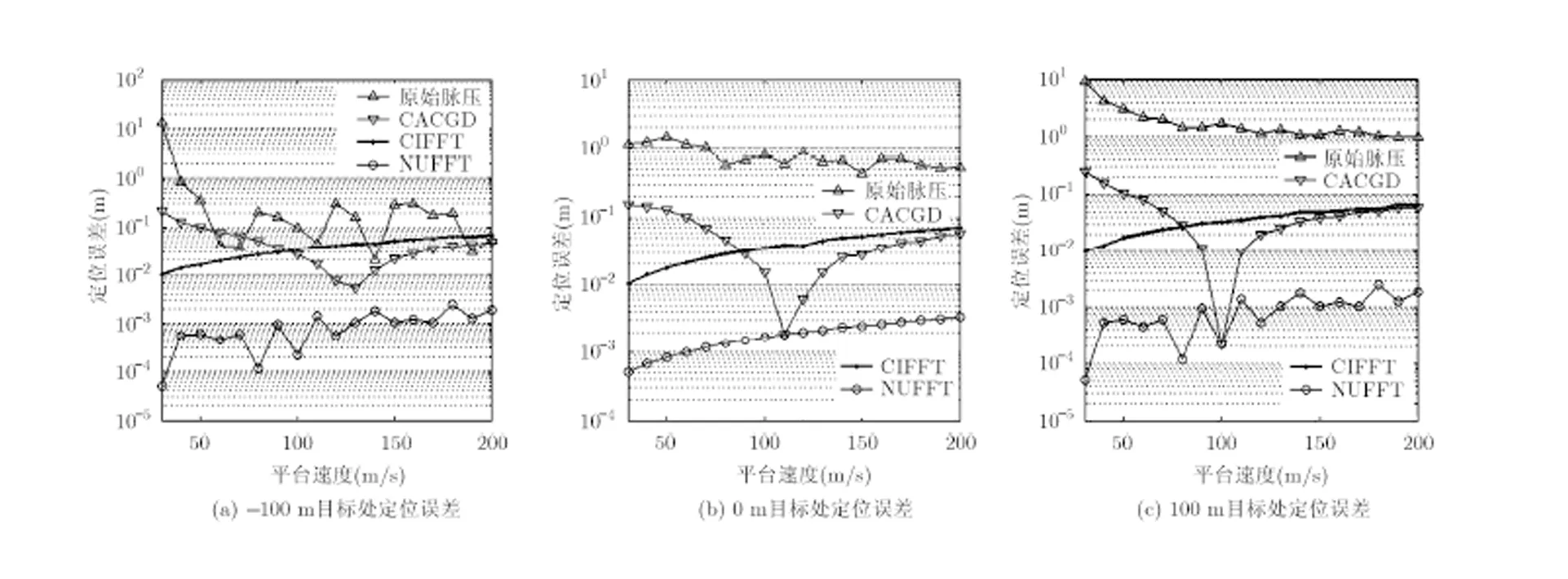
图7 定位误差与平台速度关系

图8 目标几何形变与平台速度关系

图9 4种算法相位的相对误差(平台速度50 m/s)

5 结束语

本文提出的基于NUFFT的SAR方位向运动补偿算法充分利用算法内核中FFT的快速计算特性，在运算时间上与原始脉压算法处于一个量级，成像后数据的幅度信息和相位信息同时有效。仿真和实测速度数据实验结果表明：NUFFT算法几何形变与CIFFT算法几何形变一致，NUFFT算法定位误差小于其它3种算法定位误差，NUFFT算法性能对沿航向速度误差具有很强的鲁棒性。综上，本文算法为工程化实现和实际数据处理提供了一种新的解决途径。

[1] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 61-69, 141-149.

Bao Zheng, Xing Meng-dao, and Wang Tong. Radar Imaging Technique[M]. Beijing: Electronic Industry Press, 2005: 61-69, 141-149.

[2] 严少石, 李悦丽, 周智敏. 机载UWB SAR实时图像帧几何形变分析与校正[J]. 信号处理, 2011, 27(12): 1817-1823.

Yan Shao-shi, Li Yue-li, and Zhou Zhi-min. Analysis and correction of geometric distortion of airborne UWB SAR real-time image frame[J]., 2011, 27(12): 1817-1823.

[3] 黄源宝, 保铮, 周峰. 一种新的机载条带式SAR沿航向运动补偿方法[J]. 电子学报, 2005, 33(3): 458-462.

Huang Yuan-bao, Bao Zheng, and Zhou Feng. A novel method for along-track motion compensation of the airborne strip-map SAR[J]., 2005, 33(3): 458-462.

[4] 李燕平, 邢孟道, 保铮. 沿航向运动补偿的几何形变校正[J]. 西安电子科技大学学报, 2006, 33(6): 881-886.

Li Yan-ping, Xing Meng-dao, and Bao Zheng. The correction of geometric distorition for along-track motion compensation[J]., 2006, 33(6): 881-886.

[5] Fourmont K. Non-equispaced fast Fourier transforms with applications to tomography[J]., 2003, 9(5): 431-441.

[6] Capozzoli A, Curcio C, Iudice I,.. Fast imaging of vegetation on GPUs based on Non-Uniform FFTs[C]. Preceedings of the International Conference on Electromagnetics in Advanced Applications, Torino, 2011: 1205-1208.

[7] He Xue-zhi, Xu Hao, Liu Chang-chang,.. A newapproach to distributed passive radar imaging by 2-D NUFFT[C]. Preceedings of the IEEE 10th International Conference on Signal Processing, Beijing, 2010: 2067-2070.

[8] He Xin-yi, Zhou Xiao-yang, and Cui Tie-jun. Fast 3D-ISAR image simulation of targets at arbitrary aspect angles through non-uniform Fast Fourier Transform (NUFFT)[J]., 2012, 60(5): 2597-2601.

[9] Szuster M L. A high bandwidth non-destructive method for characterizing simple media[R]. Air Force Institute of Technology Air University, 2012.

[10] Zhang Kang and Kang J U. Graphics processing unit-based ultrahigh speed real-time fourier domain optical coherence tomography[J]., 2012, 18(4): 1270-1278.

[11] Kruizinga P, Mastik F, De Jong N,..Plane-wave ultrasound beamforming using a nonuniform fast fourier transform[J].,,2012, 59(12): 2684-2691.

[12] Klein T, Wieser W, Eigenwillig C M,.. Megahertz OCT for ultrawide-field retinal imaging with 1050 nm Fourier domain mode-locked laser[J]., 2011, 19(4): 3044-3062.

[13] Wen Bin and Zabaras N. An image-based method for modeling the elasto-plastic behavior of polycrystalline microstructures based on the fast Fourier transform[R]. Cornell University, 2013.

[14] Clemente C and Soraghan J J. Vibrating target micro- Doppler signature in bistatic SAR with a fixed receiver[J]., 2012, 50(8): 3219-3227.

[15] Ban Yi-fang and Yousif O A. Multitemporal spaceborne SAR data for urban change detection in China[J]., 2012: 5(4): 1087-1094.

[16] Dai C Y and Zhang X L. Bistatic polar format algorithm based on NUFFT method[J]., 2011: 25(4): 2328-2340.

邢 涛： 男，1986年生，博士生，研究方向为雷达总体技术与雷达成像.

李 军： 男，1982年生，博士，工程师，研究方向为雷达总体技术与雷达成像.

王冠勇： 男，1989年生，硕士生，研究方向为雷达总体技术与雷达成像.

胡庆荣： 男，1974年生，博士，研究员，博士生导师，研究方向为雷达总体技术与雷达成像.

An Along-track Motion Compensation Algorithm Based onNon-Uniform Fast Fourier Transform (NUFFT) for SAR

Xing Tao①Li Jun②Wang Guan-yong①Hu Qing-rong①

①(,100854,)②(,,’710071,)

The non-equispaced along-track motion has serious impact on SAR imaging. The SAR images are geometric distorted after the along-track motion compensation, which may impair the quality of the sub-image connection and the multi-spectral SAR image fusion. When the along-track velocity error is large the remained geometric distortion after the interpolation geometric distortion correction can not be ignored. In this paper, a SAR motion compensation algorithm is presented based on Non-Uniform Fast Fourier Transform (NUFFT) directly to the azimuth non-equispaced data. The algorithm has 1 to 2 quantitative reduction in location error and geometric distortion than interpolation geometric distortion correction algorithm and has high robustness on along-track velocity error. At the same time, the amplitude and phase information can both be saved based on the proposed algorithm. The results of the NUFFT compensation for simulated data and the real SAR data verify the effectiveness of the proposed algorithm.

SAR; Motion compensation; Geometric distortion correction; Non-Uniform Fast Fourier Transform (NUFFT)

TN958

A

1009-5896(2014)05-1023-07

10.3724/SP.J.1146.2013.00969

邢涛 1mingzongyue@163.com

2013-07-04收到，2013-11-28改回