基于分布式两坐标雷达网络的目标三维跟踪算法<

严俊坤 戴奉周 刘宏伟 保 铮



基于分布式两坐标雷达网络的目标三维跟踪算法<

严俊坤*戴奉周 刘宏伟 保 铮

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

针对目前的航空管理和作战指挥系统的需求，该文提出一种基于分布式两坐标(2D)雷达网络的目标3维跟踪算法。首先，该文从集中式框架下融合中心的广义量测方程出发，推导了融合中心的更新方程。而后，将更新方程中的量测用各部雷达的局部跟踪信息来代替，并由此得出目标3维状态的估计。从推导过程可知，该文所提算法是量测扩维的集中式融合算法通过矩阵变换直接得到的，只是变换过程中对单雷达跟踪模型进行了近似，因此是次优的。最后，蒙特卡罗仿真实验表明，该算法收敛速度很快，且跟踪精度很高，可以满足实际需求。

两坐标(2D)雷达；雷达组网；目标3维跟踪

1 引言

在目前的航空管理和作战指挥系统中，需要获取目标的3维信息。常见的目标3维定位和跟踪方法包括以下几种方式：(1)3坐标雷达直接测量[1]；(2)两坐标(2D)雷达配合测高雷达进行测量[2]；(3)在假设目标匀速、等高飞行的情况下，利用单部雷达对目标进行3维跟踪[3]。在方式(1)中，3坐标雷达可以实时、精确地测出目标的3维信息；但缺点在于3坐标雷达的生产和维护成本很高，且技术复杂。在方式(2)中，两坐标雷达负责测量目标的距离和方位等信息，结合测高雷达提供的高度信息，可以得到目标的3维位置信息。这种方式实现技术比较简便，目前应用比较广泛；但是这种方式的测量过程较为复杂，难以满足实时性的需求，而且由于需要配备测高雷达，不适用于常规的2D雷达系统。方式(3)的主要思想是将目标的初始状态表示为一个混合高斯分布的形式，该分布中每个分量的初始高度不同，在各个分量上独立地进行扩展Kalman滤波，并将它们的结果进行融合即可得到目标的3维状态[3]。这种方式应用条件比较苛刻，且收敛性较差，因此在实际中难以得到应用[4]。

综上可见，如何在2D雷达组网系统中进行目标3维跟踪仍是一个难题。在考虑工程应用中传输带宽和融合中心的处理能力的前提下，本文研究了分布式处理结构[13]下2D雷达组网对单个目标进行3维跟踪的问题。首先，本文从集中式框架下融合中心的广义量测方程出发，推导了融合中心的更新方程。而后，本文将更新方程中的量测用各部雷达的局部跟踪信息来代替，并由此得出目标的3维状态。从推导过程可知，本文算法是量测扩维的集中式融合算法通过矩阵变换得到的，只是在变换过程中对单雷达跟踪模型进行了近似，因此是次优的。最后，本文对所提算法进行了有针对性的仿真，并将结果与文献[11]进行了比较。结果表明，该算法收敛速度很快，跟踪精度很高，可以满足实际需求。

2 目标运动模型

假设在3维空间中有一个近似匀速飞行的目标，目标的运动模型[14]可描述为

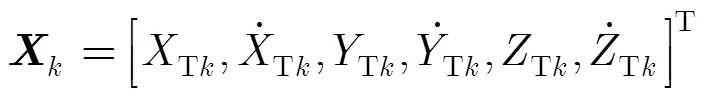
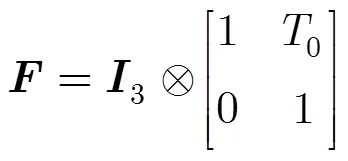
3 单雷达2D跟踪模型

3.1局部状态模型

在第个雷达节点，目标的2D运动模型可近似为 1)

3.2单雷达观测模型

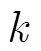
单部雷达的2D跟踪滤波采用转换量测模型[15]，第部雷达的观测模型可写成

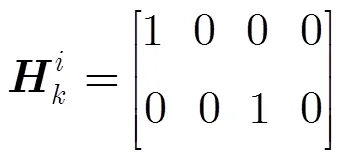
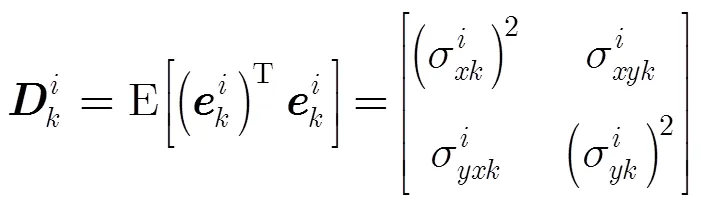
基于式(5)和式(10)，并采用信息式的Kalman滤波器，第部雷达的局部更新方程[15]可表示为

3.3局部状态与目标3维状态的关系

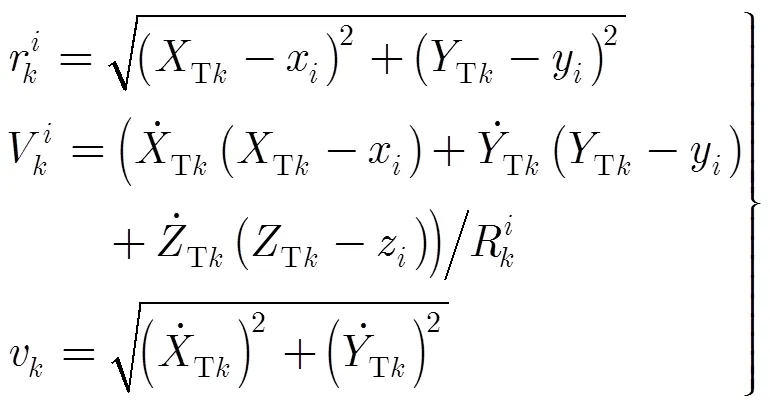
图1 第i个雷达节点的局部状态与目标3维状态的空间位置关系

总的来说，本节介绍了单部雷达的跟踪模型。下节将从集中式框架下的融合思想出发，介绍一种次优的分布式估计融合算法。该算法将各部雷达的局部跟踪信息融合，进而得到目标的3维跟踪信息。

4 融合中心的目标3维跟踪

首先给出集中式框架下的融合中心广义量测方程：

其中，

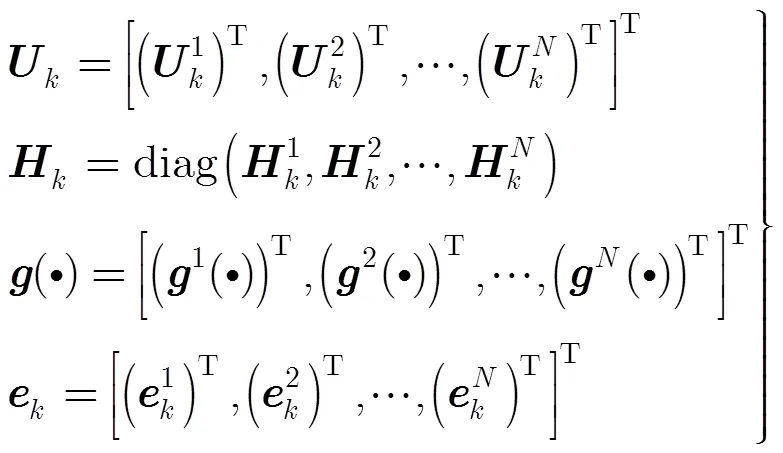
利用式(17)和式(18)的块对角性质，融合中心在时刻的集中式航迹估计和相应的误差协方差矩阵为

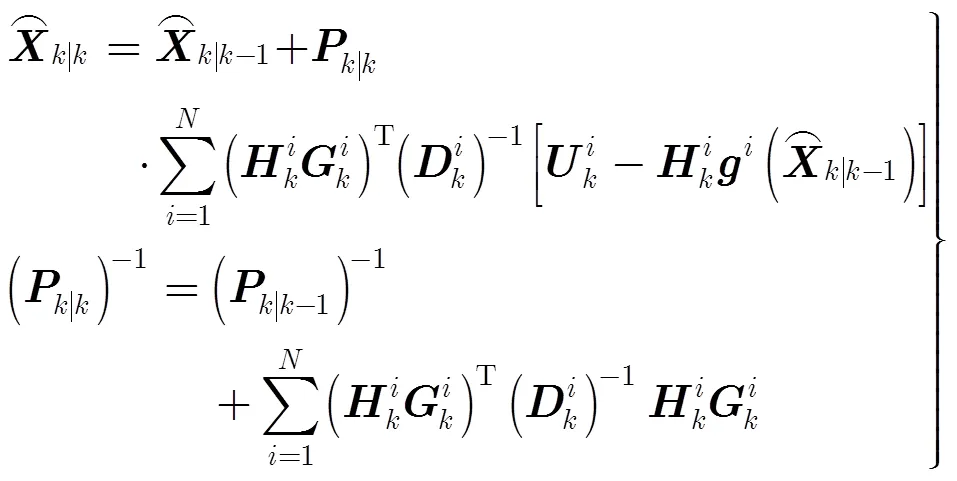
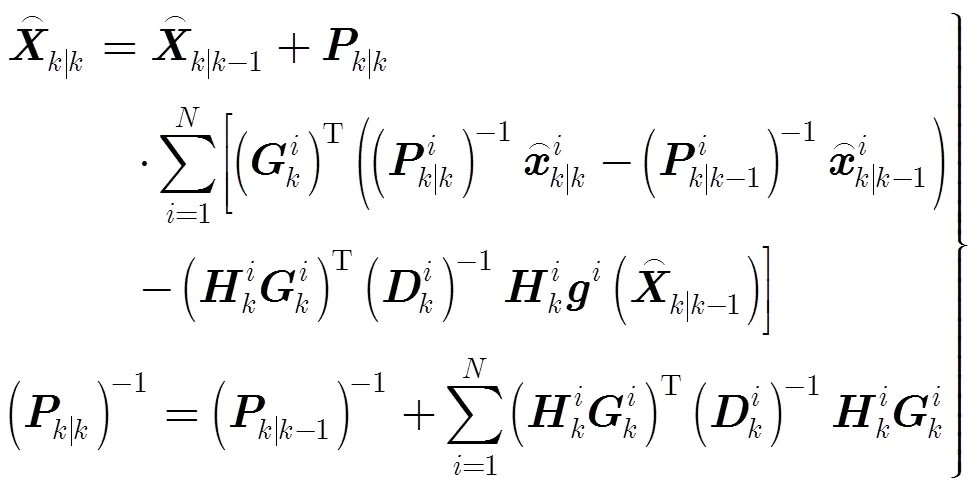
将式(13)的第2项代入式(22)的第2项中，可得到中心估计器协方差更新方程的另一种形式：

由以上的推导过程可知，这种融合算法完全是量测扩维的集中式融合算法通过矩阵变换得到的，只是在变换过程中对各部雷达的局部跟踪模型进行了近似，因此是次优的。在这种算法中，融合中心需要各部雷达提供如式(24)的估计量：

5 3维滤波器的初始状态选取

上节已经给出了一种分布式处理框架下的目标3维跟踪算法。在实际跟踪中，滤波器初始解的选取也会极大地影响跟踪性能[4]。因此，本文根据文献[10]的思想，利用ML估计给目标3维跟踪提供一个初始解。

假设目标在前帧服从匀速运动的模型，其中表示ML估计目标初始状态时所用的帧数。由于各部雷达不同时刻的观测误差相互独立，观测的似然函数可写为

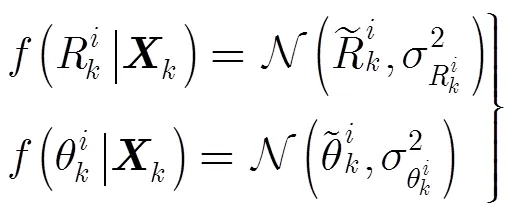
这样就能获得目标3维状态的ML估计。

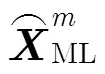
6 实验结果分析

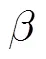
仿真考虑了两种布阵情况：在第1种情况中，目标的初始位置位于(22.75,0,) km，并以速度为(100,50,0) m/s匀速飞行(等高飞行)；在第2种布阵形式中，考虑了目标匀速降落的情况，目标初始位置在(50,0,) km，速度为(-200,50,-20) m/s(仿真中取=5 km和=15 km)。图2给出了两种布阵情况中，雷达与目标的相对位置关系。

图2 雷达与目标的空间位置关系

为了验证第4节中给出的算法的有效性，本文对其进行了仿真。图3给出了ML估计的精度和估计误差的CRLB随所用帧数变化的示意图。本文中，目标位置和速度估计的均方根误差(RMSE)被定义为

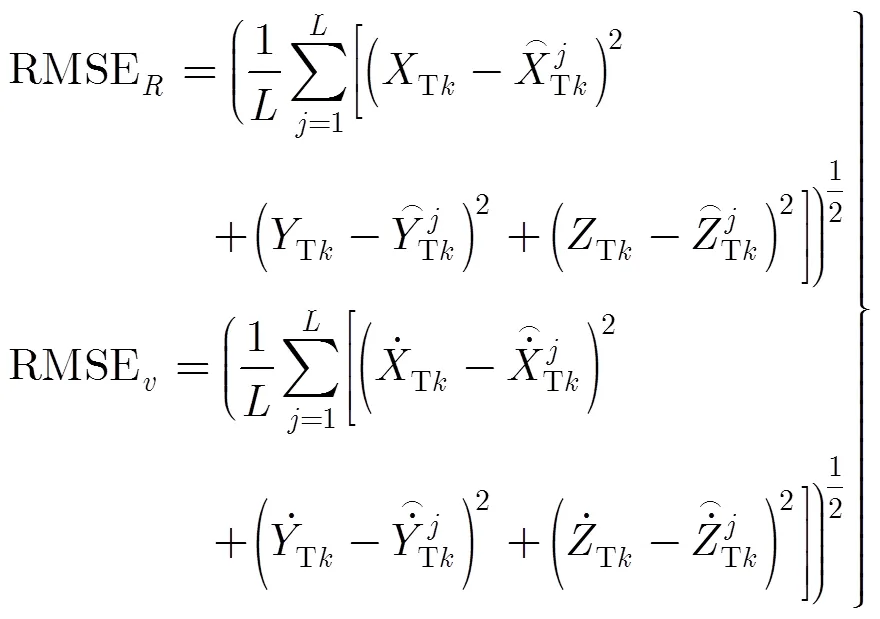
图3 ML估计结果

图4中，BCRLB表示集中式框架下目标3维跟踪的贝叶斯CRLB(BCRLB)[14]，它给目标跟踪误差提供了一个下界，具体推导见文献[14]。由图4的结果可以发现，大约在6步滤波以后，目标的跟踪精度可收敛至BCRLB附近，这也表明了本文方法能够很好地解决分布式处理结构下2D雷达组网目标3维跟踪的问题。除此之外，由图4的结果还可以发现：(1)目标的飞行高度越高，目标的跟踪精度越高；(2)当目标远离雷达网络时，跟踪性能随之下降。

为了验证算法的性能，本文还将跟踪的结果与文献[11]提出的算法进行了比较，具体参数与前面仿真相同，但只用了雷达1和雷达2(文献[11]的算法只适用于两部雷达的情况)。图5给出了两种算法在=15 km时高度估计的RMSE。结果表明，本文算法的收敛性要明显优于文献[11]给出的算法，从而进一步验证了本文算法的有效性。

7 结束语

图4 目标跟踪的RMSE

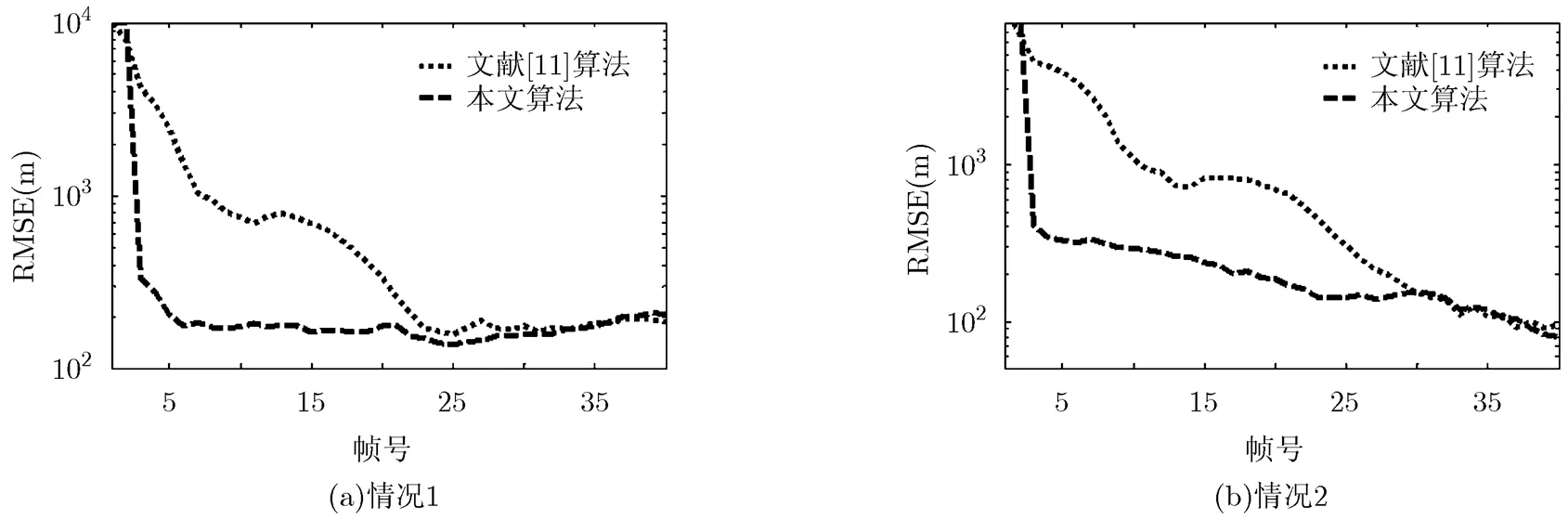
图5 高度估计误差的RMSE

[1] Park S E and Lee J G. Improved Kalman filter design for three-dimensional radar tracking[J]., 2001, 37(2): 727-739.

[2] 庞志兵. 测高雷达与二维雷达数据融合问题研究[J]. 指挥控制与仿真, 2006, 28(4): 10-12. Pang Zhi-bing. Study on height finder radar and data fusion of two-dimensional radar[J].&, 2006, 28(4): 10-12.

[3] Gai Ming-jiu, Yi Xiao, He You,.. An approach to tracking a 3D target with 2D-radar[C]. Proceedings of Radar Arlington, VA, 2005: 763-768.

[4] Aoki E H. A general approach for altitude estimation and mitigation of slant range errors on target tracking using 2D radars[C]. Proceedings of Information, Fusion, Edinburgh, UK, 2010: 756-759.

[5] Manolakis D E. Efficient solution and performance analysis of 3-D position estimation by trilateration[J]., 1996, 32(4): 1239-1248.

[6] Zhao S B, Chen M, and Lee T H. Optimal placement of bearing-only sensors for target localization[C]. Proceedings of Amarican Control, Montreal, Canada, 2012: 5108-5113.

[7] Amato F and Golino G. Accuracy of height estimation by a system of 2-D netted radars[C]. Proceedings of Radar, Rome, Italy, 2011: 773-776.

[8] Luo Zhi-yong and He Jia-zhou. ML estimation of true height in 2-D radar network[C]. Proceedings of Information Fusion, Quebec, Canada, 2007: 1-7.

[9] 吴跃波, 杨景曙, 王江. 一种双基地MIMO 雷达3维多目标定位方法[J]. 电子与信息学报, 2011, 33(10): 2483-2488.

Wu Yue-bo, Yang Jing-shu, and Wang Jiang. A method for multi-target 3D localization in bistatic MIMO radar[J].&2011, 33(10): 2483-2488.

[10] Yothin R, Ru Ji-feng, Siva S,.. Altitude estimation for 3-D tracking with two 2-D radars[C]. Proceedings of Information Fusion, Chicago, USA, 2011: 1-8.

[11] 熊伟, 潘旭东, 彭应宁, 等. 分布式2D雷达网的高度估计技术[J]. 信息与控制, 2010, 39(4): 408-412. Xiong Wei, Pan Xu-dong, Peng Ying-ning,. Technology of height estimation in distributed 2D radar network[J]., 2010, 39(4): 408-412.

[12] 苗高洁, 丁春山, 卢元磊, 等. 2D雷达目标跟踪中的高度估计[J]. 指挥控制与仿真, 2011, 33(4): 33-37. Miao Gao-jie, Ding Chun-shan, Lu Yuan-lei,Height estimation in 2D radar target tracking[J].&, 2011, 33(4): 33-37.

[13] 曾涛, 殷丕磊, 杨小鹏, 等. 分布式全相参雷达系统时间与相位同步方案研究[J]. 雷达学报, 2013, 2(1): 105-110. Zeng Tao, Yin Pi-lei, Yang Xiao-peng,time and phase synchronization for distributed aperture coherent radar[J]., 2013, 2(1): 105-110.

[14] 严俊坤, 戴奉周, 秦童, 等. 一种针对目标3维跟踪的多基地雷达系统功率分配算法[J]. 电子与信息学报, 2013, 35(4): 901-907. Yan Jun-kun, Dai Feng-zhou, Qin Tong,.. A power allocation approach for 3D target tracking in multistatic radar systems[J].&2013, 35(4): 901-907.

[15] 韩崇昭, 朱洪艳, 段战胜. 多元信息融合[M]. 第2版, 北京: 清华大学出版社, 2010: 231-254.

[16] Greco M, Stinco P, Gini F,.. Cramér-Rao Bounds and selection of bistatic channels for multistatic radar systems[J]., 2011, 47(4): 2934-2948.

[17] Rao S S. Engineering Optimization: Theory and Practice [M]. 3rd Edition, New York: Wiley, 1996: 383-425.

严俊坤： 男，1987年生，博士生，研究方向为认知雷达、目标跟踪与定位、协同探测.

戴奉周： 男，1978年生，博士，讲师，研究方向为统计与自适应信号处理及其在雷达信号处理和目标检测中的应用.

刘宏伟： 男，1971年生，博士，教授，博士生导师，研究方向为雷达系统、雷达信号处理、雷达自动目标识别等.

A 3D Target Tracking Algorithm in Distributed 2D Radar Network

Yan Jun-kun Dai Feng-zhou Liu Hong-wei Bao Zheng

(,,710071)

In order to satisfy the requirement of the air traffic control and the battle-filed command system, a three-dimensional (3D) tracking algorithm in distributed two-dimensional (2D) radar network is proposed. Firstly, this paper starts from the generalized measurement equation at the fusion center under the centralized framework, and derives the update equation. Then, the target 3D state is estimated by substituting the measurement term in the update equation with each local radar tracking information. Judging from the derivation, the proposed algorithm is obtained by centralized fusion method with measurement expansion and matrix transformation directly, and it is a suboptimal algorithm due to the approximation of the tracking model of single radar. Finally, Monte Carlo simulations show that the proposed method has fast convergence speed and achieves good tracking accuracy, thus it can meet the need of the real application.

2D radar; Radar network; Target 3D tracking

TN953

A

1009-5896(2014)05-1055-07

10.3724/SP.J.1146.2013.00469

严俊坤 jkyan@stu.xidian.edu.cn

2013-04-09收到，2014-01-14改回

国家自然科学基金(61271291, 61201285)，新世纪优秀人才支持计划(NCET-09-0630)和全国优秀博士学位论文作者专项资金(FANEDD- 201156)资助课题