往复压缩机管道系统振动计算方法的研究
2014-05-29郭景宏苏景武王芝杰
郭景宏 苏景武 王芝杰
(1.天华化工机械及自动化研究设计院有限公司;2.青海盐湖镁业有限公司)
往复压缩机主要应用于石油化工、化学化工等领域,但管道振动问题一直存在并影响着往复压缩机工作性能。通常往复压缩机共振是振动发生的主要原因,往复式压缩机周期性吸排气产生气流脉动,当管道结构固有频率、管道内气柱固有频率与压缩机气流脉动激发频率接近时,就会引起管道剧烈振动,使管道与其附件的连接部位易发生松动和破裂,威胁装置的安全运行。
近几年,国内外对振动的研究工作主要集中在以下几个方面:完善转移矩阵,通过数值模拟和实验[1],但这些研究主要侧重于简单管道气柱固有频率;转移矩阵是建立在一维数学模型基础上的,故计算复杂管系气柱固有频率时,显得较为繁琐且计算值较为粗略[2]。笔者在前人研究的基础上,用有限元法模拟几何形状复杂管道,以某石化厂往复式压缩机复杂主管道的振动分析为例,通过分析包括三通管、弯头的管道,得出研究气柱固有频率和管道结构固有频率的计算方法,为识别往复压缩机管线振动提供了方法和理论依据。
1 基本理论
1.1气柱固有频率有限元方程的建立
对于压缩机管道内气体,有以下几点假设:该气体为无粘性、可压缩气体;气体平均速度、平均压力和平均密度在该管道方向上是定值;对于该气体只考虑气体脉动影响。
压缩机管道气柱声学波动方程可写为[3]:
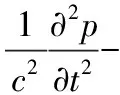
(1)
式中c——声速;
p——声压;
t——时间;
▽——拉普拉斯算子。
通过变换可得压缩机管道气柱固有频率的有限元方程[4]:
(2)
式中 [F]——总载荷列向量;
[Kp]——总刚度矩阵;
[Mp]——总质量矩阵。
由于非对称矩阵法(UNSYMMETRIC)主要用于求解模型生成的刚度矩阵、质量矩阵不对称等问题,ANSYS模拟计算中非对称法是采用完整的[K]和[M]矩阵,计算刚度和质量为非对称的问题,因此非对称法对于声学、流体-结构耦合问题的模拟求解是比较精确的。
1.2管系结构固有频率和振型向量方程的建立
在机械结构的动力分析中,利用弹性力学有限元方法建立动力学模型,进而计算出结构的固有频率和模态振型。求解管道结构的固有频率和振型时,由于阻尼影响较小,可不计阻尼的作用。因此管系的自由振动方程为[4]:

(3)
对n个自由度管系,位移向量为{x} = [x1,x2,x3,…,xn]T,[M]、[K]均为n×n阶对称矩阵。对具有足够约束的管系,[M]、[K]是正定的。
式(3)是二阶常系数齐次微分方程组,设各个位移分量作相同的简谐振动,即:
{x} = {X} sin(ωt+ψ)
(4)
式中 {X}——振幅向量,{X} = [X1,X2,X3,…,Xn]T;
ω——振动圆频率。
消去代数因子sin(ωt+ψ)得到方程组为:
([K]-ω2[M]){X} = 0
(5)
式(4)有非零解的充要条件是其特征矩阵行列式为零,即:
det([K]-ω2[M])=0
(6)

2 计算实例
2.1压缩机主管道内气柱固有频率计算
压缩机主要介质是聚丙烯,双作用、排气压力2.06MPa、转速740r/min;管径φ45mm×3.5mm、φ219mm×5mm、φ16mm×3mm。管道内气柱选用Fluid30单元,由于气柱的固有频率与振幅无关,因此可以把端点不为零的p或u设为1,此管道入口为缓冲罐,视为声学开口边界条件,管道与截止阀连接的一端视为声学上的闭口条件[1]。其ANSYS软件模型如图1所示。计算时室内温度为26℃,根据此温度查得空气的密度ρ=1.181kg/m3,声速c=346m/s。对其进行密度为10的网格划分,在缓冲器连接管道端施加约束p=0的压力载荷。选取模态分析类型,用非对称矩阵法法算出管道内气柱的前六阶固有频率值见表1。

图1 管道气柱模型图

表1 管道气柱前六阶固有频率值
2.2压缩机主管道结构固有频率计算
建模时管系的材料性能常数为:弹性模量E=210GPa,泊松比μ=0.3,密度选用ρ=7800kg/m3。定义的梁单元Beam189对管道模型进行网格划分的有限元模型如图2所示,根据现场管支架约束施加边界条件的有限元模型如图3所示。选取Modal分析类型,用Block Lanczos法算出管道结构的前六阶固有频率值见表2。对计算结果进行后处理做模态扩展,为了更清楚比较研究,只提取振型变形比较明显的第四、六阶振型图(图4)。

图2 管系有限元网格模型

图3 施加约束管系有限元模型

表2 管道结构前六阶固有频率值

图4 原管线的固有频率振型图
2.3激发主频率计算
往复式压缩机激发频率计算公式为[1]:
式中i——激发频率的阶次,i=1,2,…;
m——压缩机的作用方式,单作用气缸m=1,双作用气缸m=2;
n——压缩机的转速,r/min。
共振区按f=(0.8~1.2)fex计算,该压缩机的转速是740r/min,m=2得出前六阶激发频率fex、共振区频率f见表3。

表3 激发频率fex和共振区频率f
3 分析及讨论
为了更直观地研究该往复式压缩机主管线振动的原因,采用表1~3中的各阶频率作图(图5)。

图5 原管线各阶频率图
由图5可观察到,气柱固有频率不在共振区间内,管道结构固有频率的第一、四、六阶固有频率落在共振区间,且管道结构固有频率和气柱固有频率不接近,所以引起管道振动的主要原因是管道结构固有频率与激发频率发生共振产生了激烈的振动。
4 减振措施
为了提高管系的固有频率,给管线添加更多的约束条件,在靠近弯头、三通管处加上约束[5],如图6所示;计算得出的结构固有频率值见表4;并观察新管线的第四、六阶振型(图7),与原管线振型图进行比较;最后采用表1、2、4中的各阶频率作图(图8),可以看到减振效果良好。
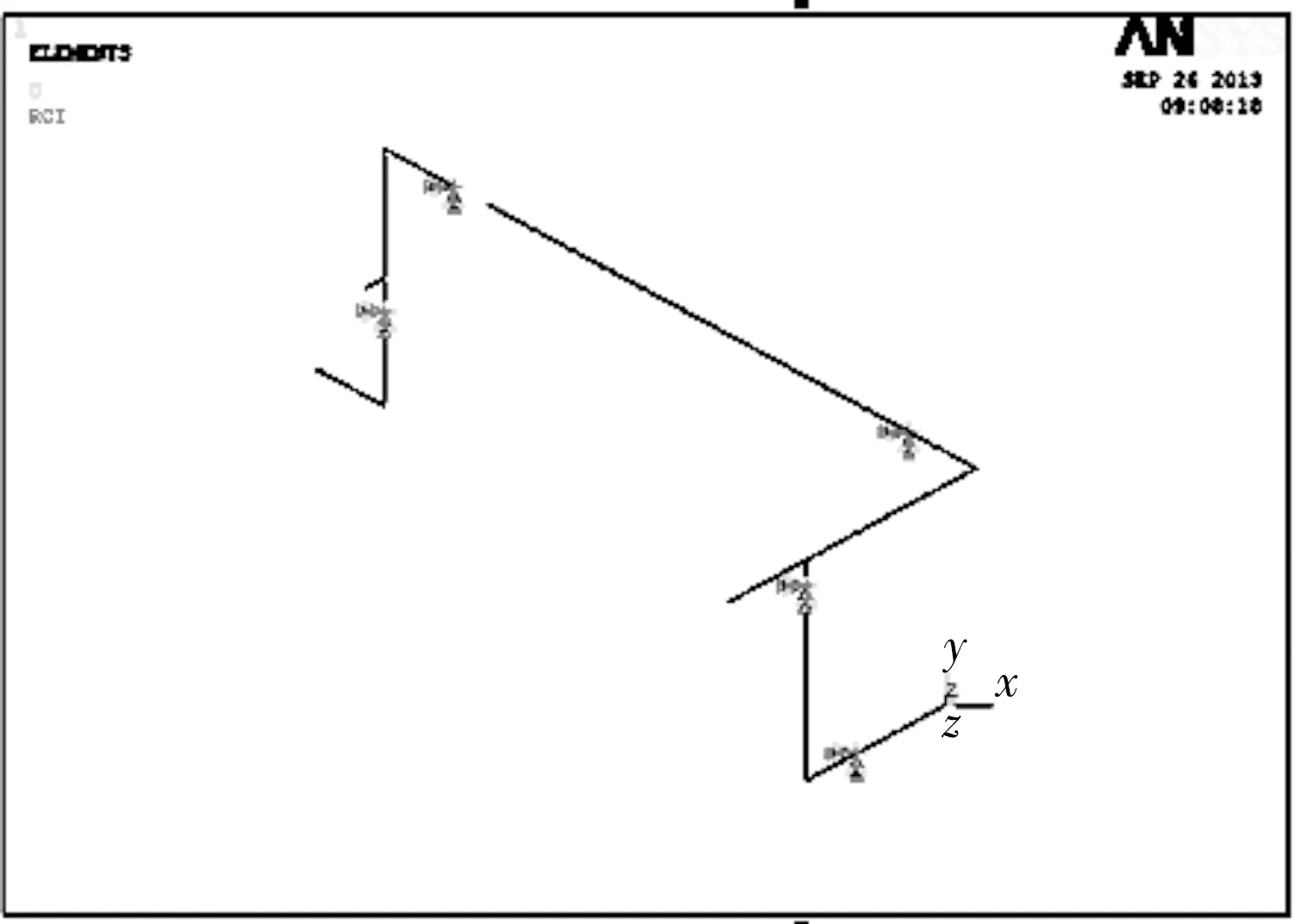
图6 管系结构有限元模型(增加约束)

表4 施加约束后管道结构前六阶固有频率值
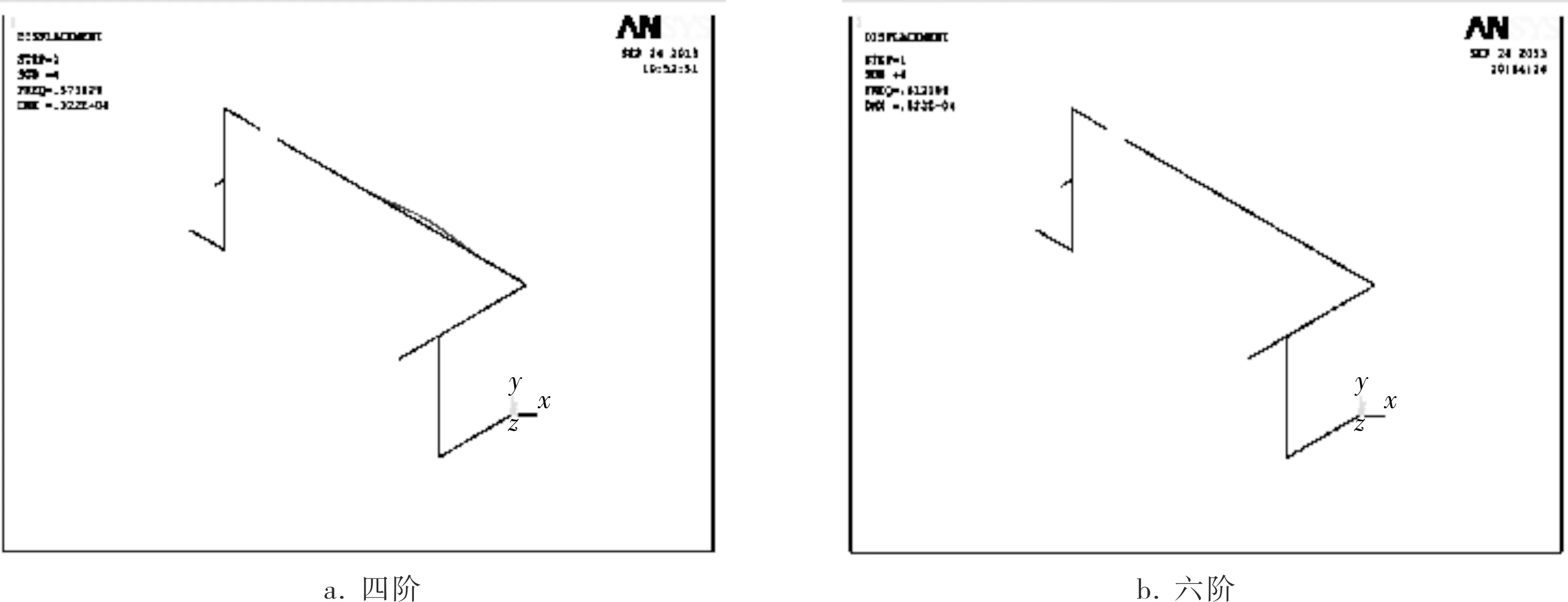
图7 新管线的固有频率振型图
通过施加更多的约束之后,管道固有频率明显提高,顺利避开了前六阶共振区;并且从相应的振型图上看出第四、六阶振动明显减弱。
5 结论
5.1管道靠近气缸管段存在弯头,这样,较大气流压力脉动在转弯处对管道会产生激振;在现场允许的前提下,尽量减少弯头,使管路走向明晰。
5.2管道系统支撑太少,管道刚度很低,由于往复压缩机激发频率较低,因此管道固有频率比激发频率越高越好,至少应该避开前六阶共振区,而提高固有频率的一项有效间接方法是在合适的位置施加相应约束条件,通过新约束,管线结构固有频率明显提高,从而顺利避开了共振区,消除了由共振引起的振动。
5.3要消除管道激烈振动,首先应该确定振动原因,一般应对管道的气柱固有频率、结构固有频率进行全面、细致的计算,对管道声学特性和结构特性进行详细分析。通常实践中经常遇到的管道振动的主要原因之一是管道共振引起的,笔者提供的计算振动的方法,通过提高结构固有频率值可以有效避免共振,所采取的措施简单易行,为实践中此类问题提供了解决方法和理论基础。所用ANSYS模态分析是结合了声学、结构和流体的方法,计算结果与理论计算吻合,为工程中复杂管道振动问题提供了新的计算方法。
[1] 徐斌,冯全科,余小玲.往复压缩机级间管路气流脉动研究[J].压缩机技术,2009,(3):1~3.
[2] 沈继忱,赵士荣,董明瑞.管道振动故障三维识别方法[J].化工自动化及仪表,2012,39(1):28~31.
[3] 党锡淇,陈守五.活塞式压缩机气流脉动与管道振动[M].西安:西安交通大学出版社,1984:7~143.
[4] 姜文全,杨帆,王茂延,等.基于 ANSYS的压缩机管系结构振动模态分析[J].噪声与振动控制,2008,28(4):13~15.
[5] 李思聪,刘智勇,纪燕飞.约束条件对往复式压缩机管系结构固有频率的影响[J].化工机械,2012,39(5):36~38.
