新型柱形圆盘涡轮搅拌桨性能的实验研究*
2014-05-29雷建勇郝惠娣
雷建勇 郝惠娣 翟 甜
(西北大学化学学院)
近年来,化工生产中高粘度液体的使用日益增多,许多高分子化合物都是高粘度物,其中又有很多非牛顿型流体,在搅拌过程中粘度还会略有变化,因此对搅拌器的要求也越来越高,即要求搅拌器能够适应粘度的变化完成搅拌操作。高粘度液体的搅拌泛指互溶的高粘度液体的混合,在工业中有分散、固体溶解及化学反应等多种非均相操作。通过研究发现,当内部液体粘度较低时,罐内流体处于湍流状态,完成不同液体的均匀混合并不困难;但随着液体粘度的增大,内部流体在叶轮附近呈层流状态,远离叶轮的地方保持静止状态,或者整体保持很小的速度旋转,这样就很难完成液体在罐内的循环,罐内出现死区,这对混合、分散、传热和反应都十分不利。因此,关于高粘度液体的搅拌,首先要解决的问题就是液体的流动和循环。在这种情况下,不能单纯的依靠增大搅拌转速来提高搅拌器循环流量,因为高粘度液体搅拌器的排出量很少,转速过高还会在高粘度液体中形成沟流,而周围液体仍为死区[1]。因此,对于高粘度的流体搅拌要求搅拌器直径与罐径之比和叶轮的宽度与罐径之比都要大。
笔者设计了新型柱形圆盘涡轮搅拌器来解决上述问题,新型柱形圆盘涡轮搅拌器圆盘外缘呈圆柱形,高速旋转下剪切性能很高。对于循环能力相对弱,分散、粉碎、剥离作用强烈,两相物性差别大的分散混合很适用,能处理粘度范围很广的流体。 新型柱形涡轮蜗杆搅拌器由在水平圆盘上焊接一周大小相等的圆柱所构成。桨叶的外径、宽度与高度之比为15∶1∶4,圆周线速度范围为0.20~2.35m/s。涡轮在旋转时造成高度湍动的径向流动,适用于气体及不互溶液体的分散和液相反应过程。涡轮搅拌器速度较大,大约在300~600r/min。涡轮搅拌器的主要优点是当能量消耗不大时,搅拌效率较高,搅拌产生很强的径向流。由于新型柱形圆盘涡轮搅拌桨结构强度比较高,因此它适用于乳浊液、悬浮液等,且其强度一般不需要进行特殊校核。为了掌握搅拌功率曲线的测定方法,了解影响搅拌功率的因素及其关联方法,笔者应用新型柱形圆盘涡轮搅拌桨,通过改变搅拌液的浓度和搅拌速率做了搅拌实验。
1 实验部分
搅拌槽采用有机玻璃制成,槽的直径为300mm,槽高(即液体深度)H为300mm,搅拌槽底部未安装挡板;搅拌桨采用柱形圆盘涡轮搅拌桨如图1、2所示;液体为羧甲基纤维素纳(CMC)水溶液重量浓度分别为0.5%、1.0%、1.5%、2.0%、2.5%;所用试剂有碘+淀粉水溶液:碘浓度为1mol/L,淀粉0.1g;亚硫酸钠水溶液:Na2SO3浓度为1mol/L[5]。
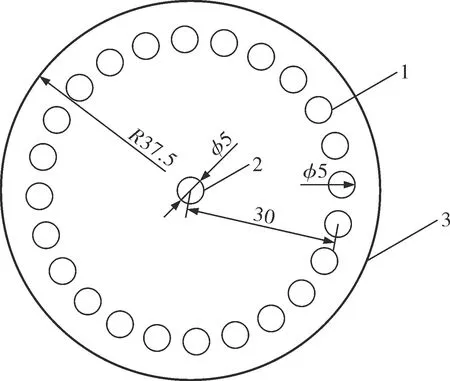
图1 柱形圆盘涡轮俯视图1——圆柱形桨叶(24个);2——搅拌轴孔;3——圆盘涡轮
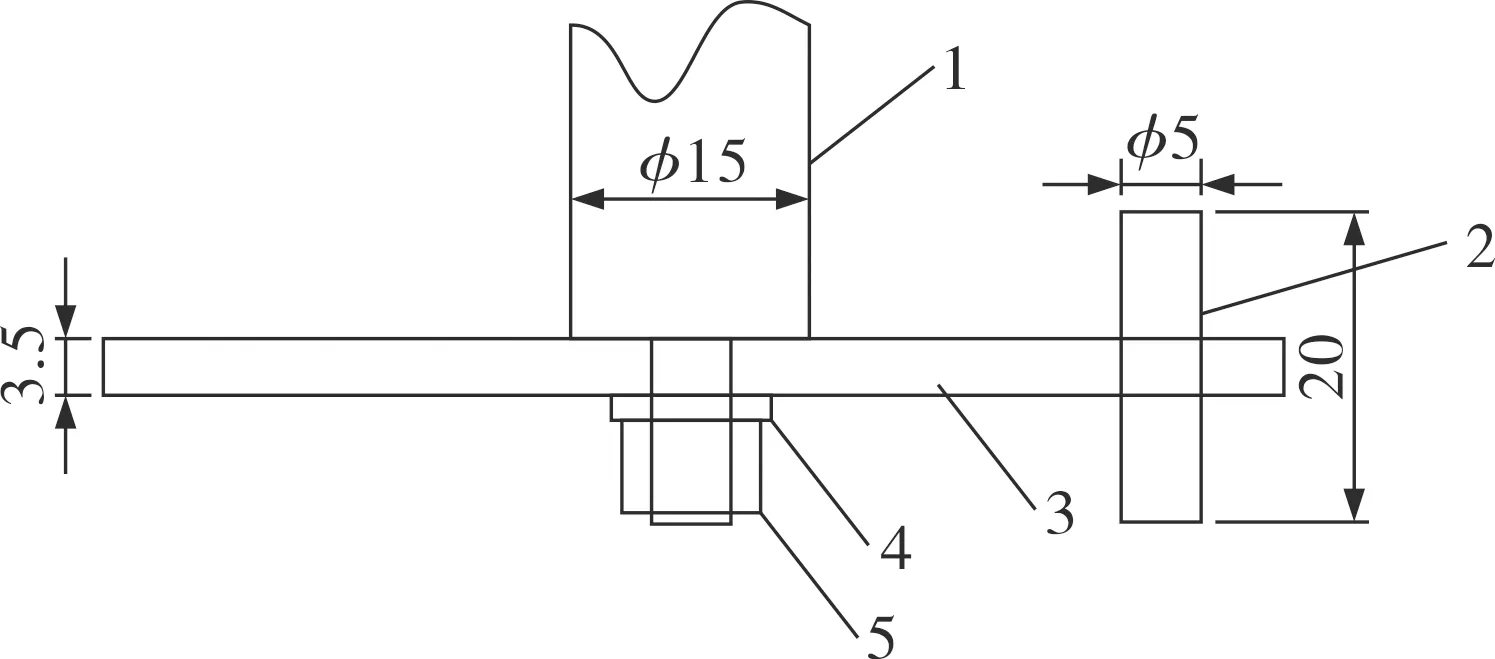
图2 柱形圆盘涡轮及搅拌轴装配主视图1——搅拌轴;2——圆柱形桨叶;3——圆盘涡轮;4——金属垫片;5——M10的螺帽
搅拌功率N是衡量搅拌设备性能的主要参数之一,通过扭矩仪测量后经计算得到。扭矩的测量方法是将扭矩转速传感器串联于搅拌轴上,由两条输出导线与微机扭矩仪相连接,将实验装置安装到位,用富士通逆变器调节转速,启动电机后在计算机上自动读取测量的扭矩数值。
2 实验结果分析及搅拌功率准数关联式的线性回归
目前,对均相系统搅拌功率的研究比较多,功率可以通过算图和数学关联式进行计算。由于这些研究结论是通过实验得出的,而实验又是在一定条件下展开的,所以应用这些算图或公式时,其搅拌器必须相同,且要满足几何条件相似。
2.1搅拌功率
搅拌功率N是指搅拌时,单位时间输入釜内物料的能量,它不包括在轴封和传动装置中损耗的能量。而搅拌设备的能量主要用于提供釜内物料进行剪切与循环,搅拌功率的目的一是用于设计或校核搅拌轴的强度和刚度;二是用于选择电动机及变速器等传动装置。影响搅拌功率的因素很多,主要有几何因素和物理因素分为两大类,包括4方面[1~4]:
a. 搅拌器的几何尺寸与转速,搅拌器直径d、桨叶宽度B、桨叶倾斜角、转速n、单个搅拌器叶片数及搅拌器安装高度等;
b. 搅拌器结构,容器内径D、液面高度H、挡板数、挡板宽度b及导流筒的尺寸等;
c. 搅拌介质的特性,液体的密度ρ、粘度μ;
d. 重力加速度g。
上述4个影响因素可关联为:
(1)
一般情况下弗鲁德准数Fr的影响较小,即c=0则有Frc=1,而容器的内径D及挡板宽度b等几何参数可以归结到系数K。由式(1)得搅拌功率N、Np为:
N=Npρn3d5
(2)
Np=K(Re)b
(3)
式中,ρ、n、d为已知数,故计算搅拌功率的关键是求得功率准数Np。在本实验中,可以测得转速、扭矩,从而可由式(1)求出Np和Re,可由式(2)求出功率N。
2.1.1搅拌转速
由点线图(图3)可知,搅拌功率N随搅拌转速n的增加呈指数形式增加,两者的关系符合N∝n3;图中直线为两者的变化趋势,可看出两者为正相关。
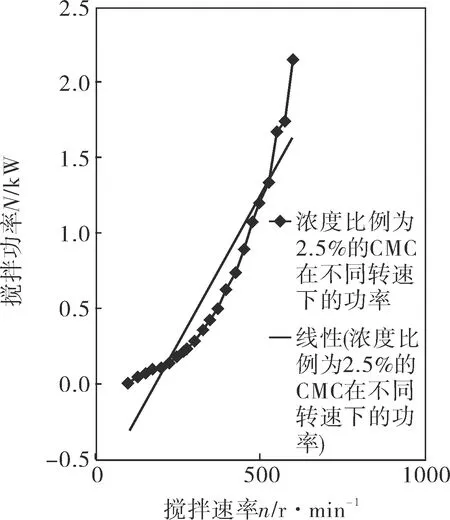
图3 不同转速下的搅拌功率
2.1.2Re-Np的关系
从图4可以看出,当搅拌雷诺数Re相同时,CMC溶液浓度比例越高,其对应的搅拌功率准数越大;当CMC溶液浓度比例一定时,搅拌雷诺数Re越大,其对应的搅拌功率准数Np越小;无论CMC溶液浓度比例如何,搅拌雷诺数Re与搅拌功率准数Np呈示负相关。

图4 不同浓度下Re-Np关系
点线图(图5)为CMC溶液浓度比例为1.5%时,不同转速下所得的平均搅拌雷诺数Re与平均搅拌功率准数Np关系图,通过多次实验求其平均值,在减小实验误差的基础上,进一步验证当Re<10时,Re与Np呈负相关性,线图为Re与Np的对数趋势图[6,7];当25>Re>10时,随着Re的增加,Np一直处于波动状态;当Re>25时,随着Re的增加,Np的下降趋势变缓且处于稳态变化。
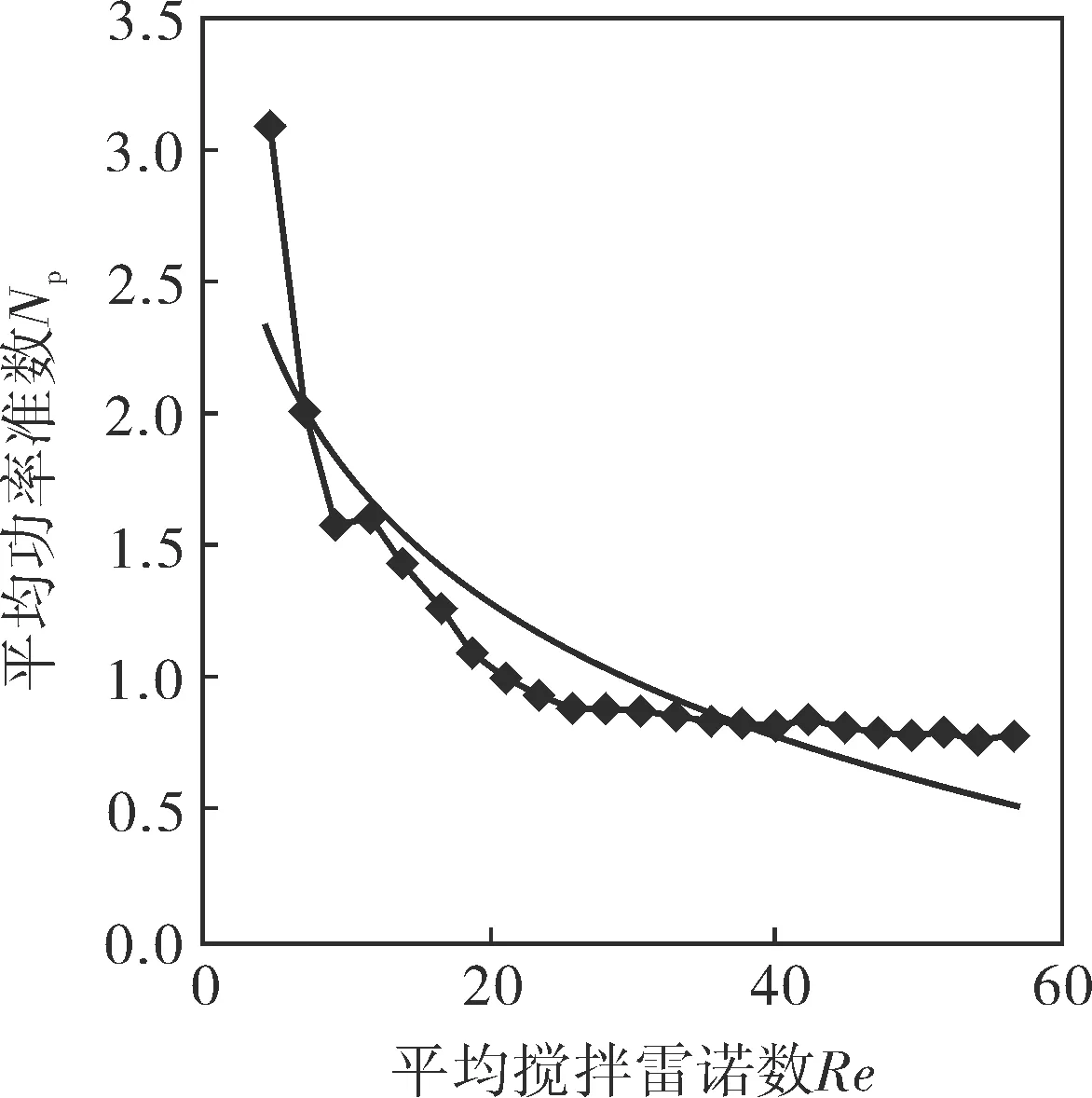
图5 Re-Np关系及对数趋势
2.2搅拌功率准数关联式的线性回归
对式(3)两边取对数可知:
lgNp=lgK+blgRe
(4)
CMC溶液浓度比例为1.5%时,通过改变电机的频率,进而改变电机的搅拌转速,计算机安装有自编测量扭矩程序,可自动记录搅拌速度、搅拌扭矩等测量数据,bong可自动保存记录结果。利用实验的多组数据计算出平均Re和平均Np(表1)并利用Matlab进行线性回归,即可以求出公式中K和b的值。

表1 不同转速下的Re和Np
利用表1中的数值,在Matlab中进行计算和线性回归,程序如下[8]:
“n=23,m=1 %令log10Re=x ,log10Np=y则有
x=[0.67 0.85 0.97 1.07 1.15 1.21 1.27 1.32 1.37 1.41 1.45 1.48 1.52 1.55 1.57 1.60 1.63 1.65 1.67 1.69 1.71 1.73 1.75 ];
y=[0.49 0.30 0.20 0.21 0.16 0.10 0.04 0.00 -0.03 -0.05 -0.05 -0.06 -0.07 -0.08 -0.09 -0.09 -0.09 -0.10 -0.10 -0.11 -0.10 -0.12 -0.11];
X=[ones(length(y),1),x′];Y=y′;[b,bint,r,rint,stats]=regress(Y,X);
s2=sum(r.^2)/(n-m-1);b,bint,stats,s2;rcoplot(r,rint) ;”
其中,%表示注释;b为输出未知数,即式(4)中的lgK,b;bint为b的置信区间;r为残差(列向量);rint为r的置信区间;stats为3个统计量决定系数R2,F值,F(1,n-2)分布大于F值的概率p,若p 由以上程序代码可以求出式(4)中的lgK和b的值。通过残差函数程序代码rcoplot(r,rint)可以绘制出所求得的lgK和b的置信区间残差图,通过画残差图发现第一个点的残差过大,超过了lgK的设定缺省值,为了减小误差,应该剔除,剔除异常点前、后的差异见表2。 表2 剔除异常点前、后回归模型的系数、系数置信区间与统计量 由表2可知,剔除异常点后lgK= 0.6547,由此可得K=4.5154;b=-0.4631,即剔除异常点(第一个点)后其线性回归方程为: Np=4.5154Re-0.4631 (5) 3.1搅拌功率N随转速n的增加呈指数形式增加,两者的关系符合N∝n3。 3.2当搅拌雷诺数Re相同时,CMC溶液浓度比例越高,其对应的搅拌功率准数Np也越大;当CMC溶液浓度比例一定时,搅拌雷诺数Re越大,其对应的搅拌功率准数Np反而越小;无论CMC溶液浓度比例如何,搅拌雷诺数Re与搅拌功率准数Np整体上呈负相关,随着Re的增加,Np的变化过程大致可分为瞬变区、波动区和稳态区。 3.3在本实验的基础上求得的Np与Re的关联式为Np=4.5154Re-0.4631,在生产实际中,该关联式可为搅拌罐的设计作参考,用于预测放大生产的搅拌功率等。 [1] 化工设备设计全书编辑委员会.化工设备设计全书——搅拌设备[M].北京:化学工业出版社,2003. [2] 化学工学会(日)编.搅拌、混合[M].东京:槙书店,1990. [3] 山本一夫(日).搅拌装置[M].东京:化学工业社,1984. [4] Perry R H.PERRY化学工程手册[M].北京:化学工业出版社,1992. [5] 华南工学院,大连轻工学院,天津轻工学院,等.发酵工程与设备[M].北京:轻工业出版社,1981:191~192. [6] 郝惠娣,郭笃信,魏玉梅,等.新型高效节能搅拌设备——中心龙卷流型搅拌槽[J].化学工程,2002,30(4):2. [7] 郝惠娣,孙吉兴,王刚.加高型中心龙卷流型搅拌槽液体搅拌性能研究[J].石油化工,2004,33(9):50~54. [8] 王岩,隋思涟.试验设计与MATLAB数据分析[M].北京:清华大学出版社,2012.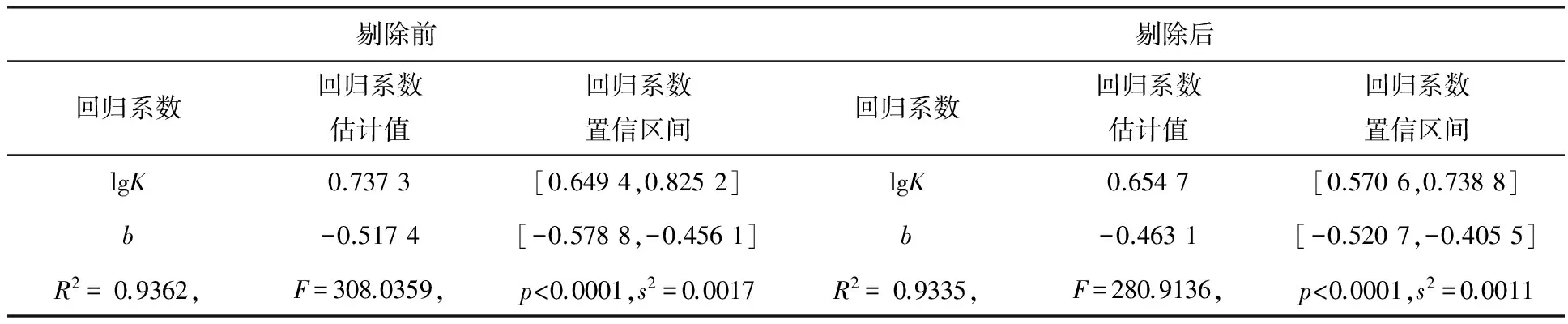
3 结论
