关于不定方程χ3+8=103y2

孙浩娜

(西南大学数学与统计学院，重庆 400715)

关于不定方程χ3+8=103y2

孙浩娜

(西南大学数学与统计学院，重庆 400715)

利用同余式和递归数列的方法，证明了不定方程χ3+8=103y2无适合gcd(χ，y)=1的整数解.

不定方程;整数解;递归数列

不定方程

(其中D是无平方因子的正整数)是一类基本而重要的不定方程，对它已有不少的研究工作．柯召和孙琦［1］证明了当D不能被3或6k+1形的素因数整除，且D≡0，1，2(mod 4)时，方程(1)无整数解(χ，y)．曹玉书［2］证明了当D是奇素数时，若D=3，则方程(1)仅有整数解(χ，y)=(11，±21);如果D≡5(mod 6)，则方程(1)无整数解．显然，对于D含有6k+1形的素因数的情况需要进一步讨论．罗明［3］证明了不定方程χ3+8=7y2仅有整数解(χ，y)=(-2，0)，(-1，±1)，(10，±12)，不定方程χ3-8=7y2仅有整数解(χ，y)=(2，0)．近些年，对于该类方程也有一些相关研究［4-7］．而当D=103时，此类方程的解还未解决．此处在此基础上，利用同余式的性质和递归数列的方法，证明了当D=103时，方程(1)无解．

定理 不定方程

无整数解．

证明 若χ≡0(mod 2)，则由式(2)有y≡0(mod 4)．这与(χ，y)=1矛盾，所以χ≡1(mod 2)．

现设χ≡1(mod 2)，此时(χ+2，χ2-2χ+4)=1或3，故式(2)有4种可能的分解:

情形1 χ+2=103a2，χ2-2χ+4=b2，y=ab．

情形2 χ+2=a2，χ2-2χ+4=103b2，y=ab．

情形3 χ+2=3a2，χ2-2χ+4=309b2，y=3ab．

情形4 χ+2=309a2，χ2-2χ+4=3b2，y=3ab．

以下分别讨论这4种情形下式(2)的整数解．

情形1 由第二式得χ=0，2，代入第一式都不成立，故该情形没有式(2)的整数解．

情形2 第二式化为(χ-1)2-103b2=-3，将第一式代入(χ-1)2-103b2=-3，得(a2-3)2-103b2=-3．由于方程X2-103Y2=-3有两个结合类解［8］，其基本解是，故全部解(X，Y)由式(3)(4)给出

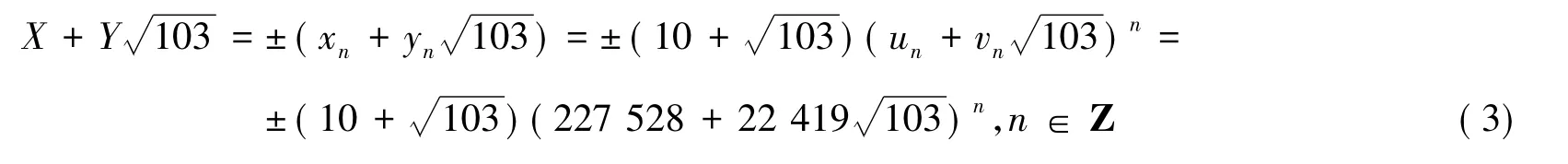
容易验证式(5)-(8)成立．

因为χ≡1(mod 2)，所以a≡1(mod 2)，所以χn≡0(mod 2)．由式(7)知，n≡0(mod 2)．

对χn的递归关系式(7)取模103，得χn≡10(mod 103)，若a2=-χn+3，则有a2≡-χn+3≡-7≡96(mod 103)，于是，矛盾．所以a2=χn+3且n≡0(mod 2)．

对式(7)取模7，得到周期为4的剩余序列．当n≡0(mod 4)时，χn≡3(mod 7)，有a2=6(mod 7)，这不可能．所以n≡2(mod 4)．

对式(7)取模17，得到周期为4的剩余序列．当n≡2(mod 4)时，χn≡7(mod 17)，有a2=10(mod 17)，于是，矛盾．故情形2无解．

情形3 由第一式知χ≡1(mod 8)，代入第二式得5b2≡3(mod 8)，这不可能．故情形3无解．

情形4 将第二式化为(χ-1)2-3b2=-3，再第一式代入得b2-3(103a2-1)2=1，因此有

因为χ≡1(mod 2)，所以a≡1(mod 2)，所以χn≡0(mod 2)．由式(9)知，n≡0(mod 2)．

对式(9)取模8，得到周期为4的剩余序列，当n≡0(mod 4)时，sn≡0(mod 8)，有7a2=1(mod 8)，此不可能．当n≡2(mod 4)时，sn≡4(mod 8)，有7a2=5(mod 8)，这也不可能．故情形4无解．

综合上述情形的讨论可知，不定方程χ3+8=103y2，χ，y∈Z，gcd(χ，y)=1无整数解．

［1］柯召，孙琦.关于不定方程χ3±8=Dy2和χ3±8=3Dy2［J］.四川大学学报:自然科学版，1981，33(2):1-5

［2］曹玉书.关于不定方程χ3±8=3Dy2［J］.黑龙江大学学报:自然科学版，1992，19(2):1-3

［3］罗明.关于不定方程χ3±8=7y2［J］.重庆师范学院学报:自然科学版，1995，12(3):29-31

［4］乐茂华.关于Diophantine方程χ3-8=py2［J］.烟台师范学院学报:自然科学版，2004，20(3):171-173

［5］黄永庆，廖江东.关于不定方程χ3±8=35y2［J］.重庆工商大学学报:自然科学版，2006，23(5):462-464

［6］谷杨华.关于不定方程χ3+1=266y2和不定方程χ3+8=133y2［J］.云南民族大学学报:自然科学版，2009，18(4):305-309

［7］梁艳华，李鑫.关于不定方程χ3+8=Dy2［J］.四川理工学院学报:自然科学版，2009，22(1):26-29

［8］柯召，孙琦.谈谈不定方程［M］.上海:上海教育出版社，1980

On Diophantine Equation χ3+8=103y2

SUN Hao-na
(School of Mathematics and Statistics，Southwest University，Chongqing 400715，China)

Congruence method and recurrent sequence are used to prove that Diophantine equation χ3+8= 103y2has no integer solution with gcd(χ，y)=1.

Diophantine equation;integer solution;recurrent sequence

O156.2

A

1672-058X(2014)01-0014-02

责任编辑:李翠薇

2013-09-04;

2013-09-28.

孙浩娜(1988-)，女，河南郑州人，硕士研究生，从事代数数论研究.