封闭系统中的货币分布状况分析*

曹茂

(重庆师范大学数学学院，重庆 401331)

封闭系统中的货币分布状况分析*

曹茂

(重庆师范大学数学学院，重庆 401331)

模型中基于个体货币的转移，近似于用类比热力学中的分子运动来研究货币的分布状况，在热力学中某一状态发生的概率，早由Blotzmann和Gibbs提出［1］。基于实际交易，引入Gini系数衡量制定的交易规则下货币分布状况;为了更加符合实际，对模型进行了改进，引入每次交易成功的概率r，其中r由交易过程中的一些影响因素作用而随机生成，经过分析得出更具有现实意义的模型。

货币分布;交易规则;基尼系数;帕累托定律

假设一个封闭系统有N个人组成，在实际的生活与生产中可以把这每个人看成是一个基本单元，在这个系统中个体数N保持不变。初始时刻每个个体i的货币量为m，研究的模型是任意两个人进行货币交换，在现实生活中可以看作是双方交易。两个人相互交易的结果是财富Δm从一个个体的手里转移到了另一个的手里，即:

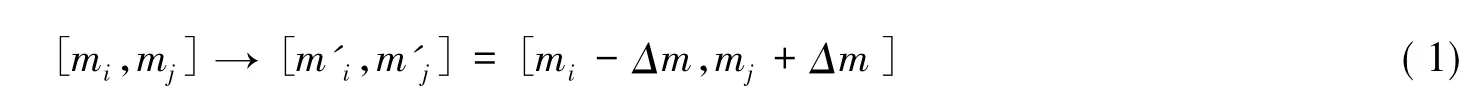
而在每一次交换的过程中系统的总货币值保持不变:

在这种情况下给出两种交易规则，讨论每个人在每种规则下，进行充分长的时间后的货币分布情况。

1 封闭系统问题分析

1.1 背景详述分析

一百多年来，帕累托定律已经得到大量的实证支持，但到目前为止对于机制的研究还没有根本性的突破。运用财富转移模型来研究财富分配的现象是近十年才出现的［2］，在此将货币视作财富的度量，因而在交易过程中货币的转移伴随着财富的转移。问题中研究的系统是封闭的，也就是系统中没有额外的财富注入，系统总财富保持不变。对于显示经济活动中的一些制约因素，诸如时间的关联，空间的关联，以及个体偏好因素在此均不予以考虑，也不考虑财富交换的某些经济活动。就像在一个封闭的容器中，有大量的分子做热运动，它们的运动是无规则的，并且两个分子在交换能量时，即任意两个分子间相互的碰撞是任意的。可以用概率分布来刻画，并且它们碰撞时相互交换能量，交换的多少也是不确定的。可以在此制定一些约束，使它们最后达到一种平衡并且分子的能量按一定的分布，但它们的总的能量保持前后不变。

1.2 交易途径

通常的交换大致可通过以下3种途径:

(1)物物交换。

(2)一种为社会全体成员乐意接受的一般商品的中介货币。

(3)信用赊账贷款，担保等方式。

但此处所考虑的仅仅是(2)中货币的交换，并且整个系统中的交易是随机的和无序的，即有:

1.3 对模型进行假设

假设两个人只要碰面就算作一次交易，因而交易会有失败和成功。失败即是不发生货币转移，成功即是发生货币转移。系统是封闭的，没有额外的财富注入，也就是说系统中总的货币量和财富值恒定。定义任意一次交易的时间为1 s，且在任意1 s中有且仅有一次交易，不考虑交易是否成功。

1.4 符号说明

M:表示封闭系统中总的货币量;mi:(i=1、2、3、 、N)表示第i个人所拥有的货币量，它随时间的变化而变化;T:表示每个人开始的平均货币量，即题中所给的m单位的货币量;n:表示在某一状态α下的具有一定货币量的人数;N:表示系统总的人数;r:每次交易成功的概率;t0:系统中的时间关联度;L0:系统空间的关联;βi:个体偏好;λ:储蓄率。

2 模型的建立与求解

2.1 模型建立

统计物理和热力学的基本定律，当一个物理系统达到热平衡时，系统的某一特定状态α发生的概率为

其中T表示温度，表示μ同一粒子的化学势能;εα表示α状态下的总能量;Nα表示在α时的具有某种能量的粒子的总数［3］;kB为常数。此概率分布就是众所周知的Blotzmann-Gibbs分布［4］。因为对于一个物理系统能达到平衡态的本质因素是系统的能量守恒，所以由此推广出，对于一个能量不变的系统，一定能够达到一个稳定态的概率分布。定义财富的概率分布p(m)为:用有的财富值在m和m+dm之间的个体数等于Np (m)dm，就像在热力学中的一样，关心概率分布p(m)平衡态［5］。

在模型中，给所有交易者相同的货币。定义任意一次交易的时间为1 s，且在任意1 s中有且仅有一次交易，不考虑交易是否成功。在某一时间一对交易者是随机选取的，接着随机选取一个交易者为“赢家”，另外一个为“输家”;他们的转移量Δm≥0从输家转移到赢家。如果输家没有足够的钱支付(mi＜Δm)，则交易失败，即双方的货币量都不变，从而进行到下一组交易者。

2.2 交易规则

交易者不允许出现负的金钱数。在交易的过程中引入式(3)、(4)制定这样的交易规则:

规则一，每次转移的货币量是一个小的定植1。

规则二，每次转移的财富值是双方货币值的平均值的随机部分:

其中(0≤ν≤1)，假定人数N为500人，总的货币量M=5×105，交易时间t=100 000 s。

3 算法实践

3.1 通过MATLAB程序进行模拟规则一

随机抽取出其中任意一种模拟结果如图1:

基尼系数:G=0．011 4。在交易规则一下，可以知道基尼系数趋近0，故而在此交易规则下的财富分配是极端平均的一种理想状态。

3.2 再用MATLAB对交易规则二进行模拟

随机抽取出其中任意一种模拟结果如图2:

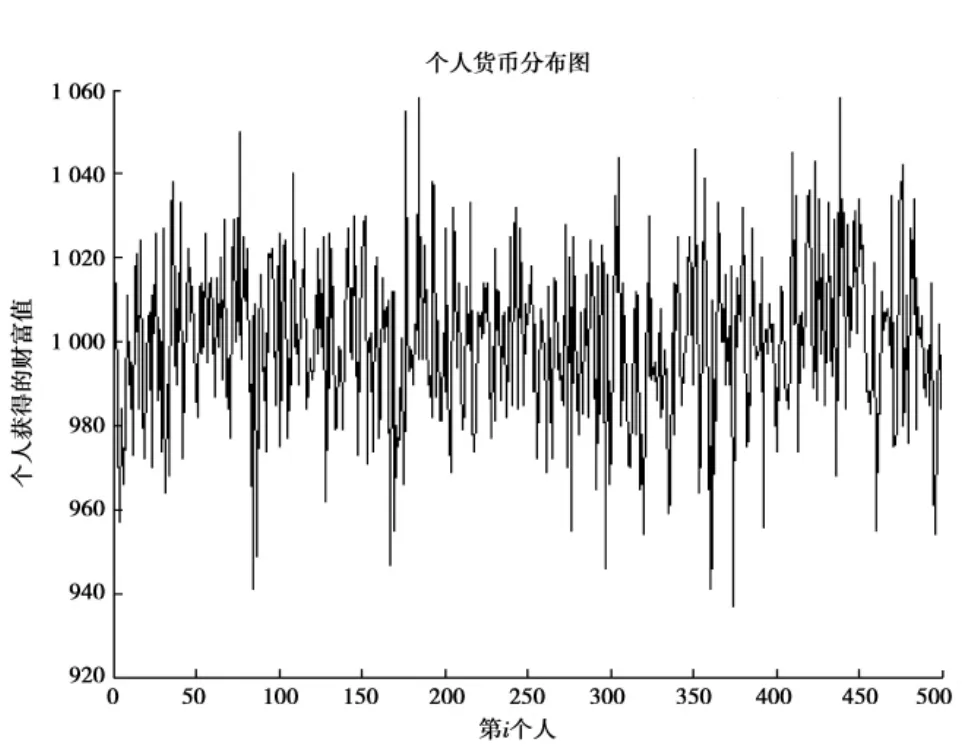
图1 规则一下个人财富货币分布

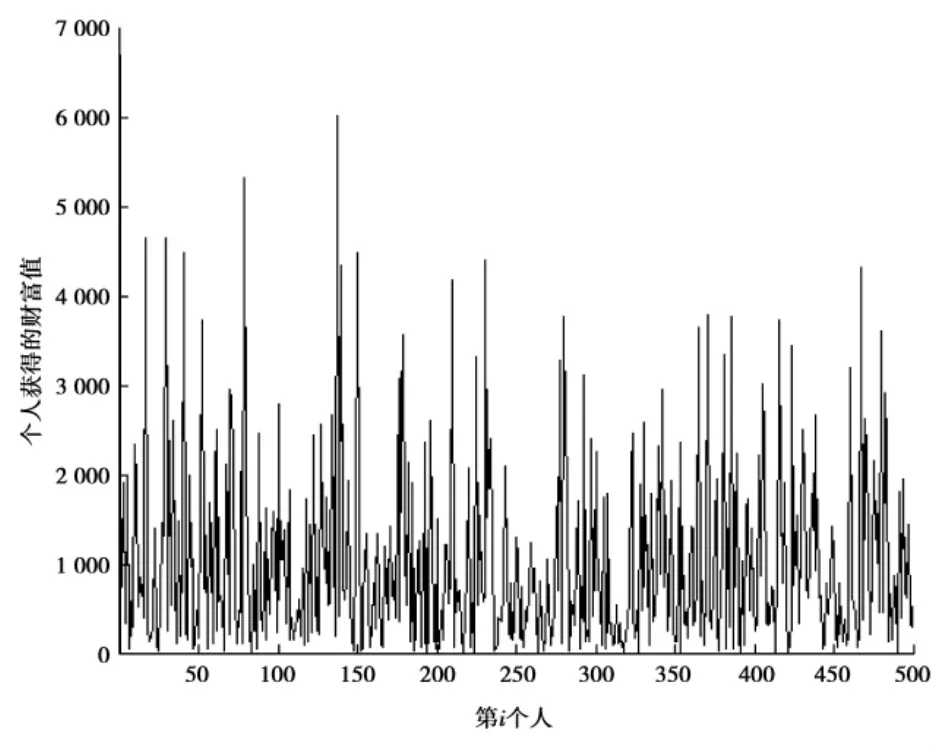
图2 规则二下个人财富货币分布

基尼系数G=0．509 9。在此交易规则下，知道基尼系数趋近0．5，因而知道系统财富分布相当不均衡，并且符合帕累托定律下的财富分配状况。

4 模型的检验

4.1 基尼系数

对于建立模型所求出的货币分布状况，引入洛伦斯模型中的基尼系数来衡量财富分配的均衡程度。用横坐标表示累积的户数或人数的百分比，用纵坐标表示累积的收入百分比。就可以画出一条从坐标原点(0，0)到坐标点(1，1)的一条向下垂的弓性线(这就是洛伦斯曲线)，这条弓形线将三角行OPM分成A、B两部分。这就是洛伦斯模型，用它来检验在设定的模型下，分配的均衡性。模型中直线OM呈45度角，为收入绝对平均线。折线OPM是绝对不平均线。洛伦斯曲线越接近绝对平均线，即A的面积越小，B的面积越大，表明收入分配越平均;洛伦斯曲线越接近绝对不平均线，即A的面积越大，B的面积越小，表明收入分配越不平均。这样就可以得到一个反应收入分配平均程度的指标——基尼系数，其计算公式是:

基尼系数总是大于0而小于1。由图3可以知道，如果A的面积不断扩大，洛伦茨曲线就趋向于正方向的两条边:OP、PM，则面积A=0．5，基尼系数G=1．0，所以基尼系数界于0于1之间，0代表绝对平均，1代表绝对不平均。基尼系数越小，收入分配越平均;基尼系数越大，收入分配越不平均［6］。

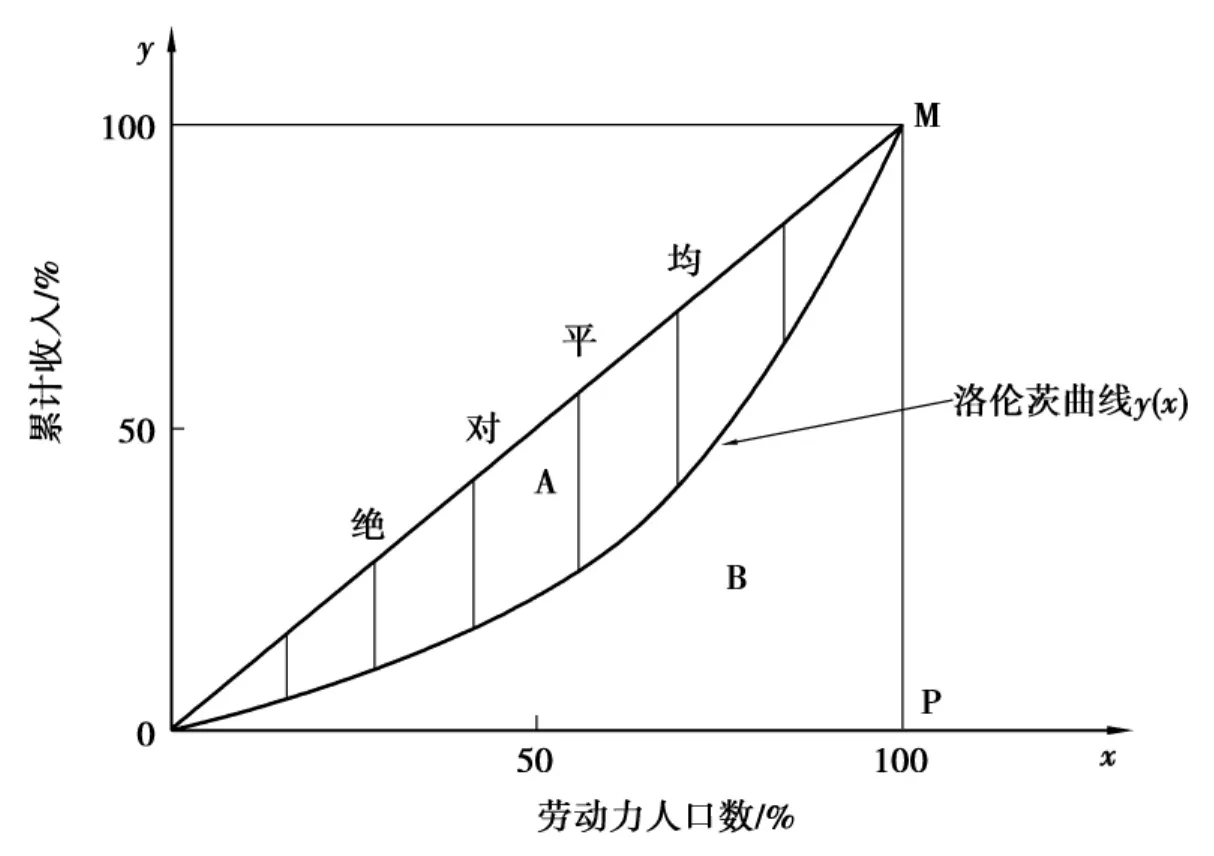
图3 洛伦茨收入

在模型中，用Gini系数定义式(2)如下:

图3中洛伦茨绝对平均曲线是表示平均财富，一个完美的分配中每个人得到同等数量的钱，这将得到值G=0，即绝对平均;另一种极端情况，某个个体得到所有的钱，则G=1，即绝对不平均。

4.2 交易规则一

进行模拟抽取一组数据可以得到如表1结果，其中基尼系数为G。

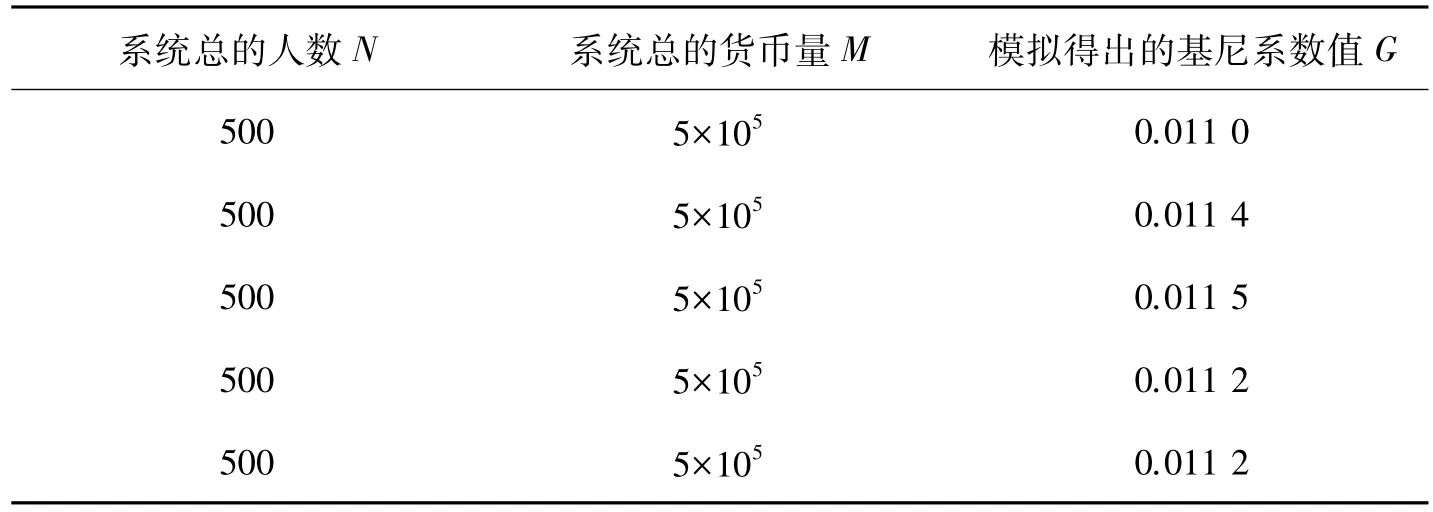
表1 多次计算机模拟选取后结果(交易规则一条件下)

通过大量模拟分析数据可以得到基尼系数趋于0．011 0。故而这种交易规则下的理想状态是所有人的财富几乎相等，也就是极端平均的状态，但在现实情况下是很难出现这种货币分布的情况，因而不具有研究价值。

4.3 对交易规则二

进行模拟抽取一组数据可以得到如表2结果，其中基尼系数为G。

表2 多次计算机模拟选取后结果(交易规则二条件下)

通过大量模拟分析数据可以得到基尼系数趋于0．5，故而这种交易规则下货币分布状况是相当不均衡的，并且满足帕累托定律下的财富分布状况，因而更具有实际意义。

5 模型的分析

5.1 实证分析

模型只是客观现实在某种程度上的近似和抽象，无论如何复杂和详尽，都不能等同于现实。经济分配模型，同样存在很多的缺点。如考虑两者之间的交换的概率是不变的并且交易量也是不变的，但在实际的过程中，这些都是变化的。这是在一种理论条件下进行的讨论，目的是在认识和深入理解模型的缺点和局限性的基础上，使模型更加完善。对于模型可以引入一系列的变量进行完善与修正，直到模型很接近实际情况［7］。

由于交易规则一模拟出来的结果是一种十分理想的状态，不具有现实意义，因而在此不做更进一步的讨论，于是讨论交易规则二(图4)。

由图4可以定性分析出获得一定货币值的人口数，并且可以估算出80%的人数获得的货币量在T= 1 000以下，仅有20%的人在T=1 000以上;也就是说明，财富分布不均，两极分化严重。20%的人掌握着80%的财富，与帕累托定律基本相符，因而具有一定的现实意义。

5.2 模型的改进

建立的模型，是以物理学意义上的分子热运动建立的。考虑到交易的随机性，并且考虑到交易的逻辑基础，即个体具有支付能力。在模型中忽略了交易成功或者失败的现实影响因素，诸如:时间的关联，空间的关联，以及个体偏好因素。

因而在此可以设系统引入每次交易成功的概率为r，在这里r由系统中的时间关联度为t0，空间的关联为L0，个体偏好为βi，储蓄率λ相互作用下随机生成的［8］。

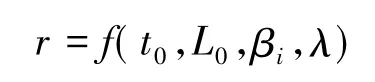
在交易时间t下，交易了t次，其中成功的次数ξ，于是有ξ～B(t，r)。交易成功的期望值Eξ=tr，故理论状态的交易次数为Eξ。用MATLAB再次对改进模型后的交易规则二进行模拟，抽取其中一模拟的结果分析，得图5～图7:

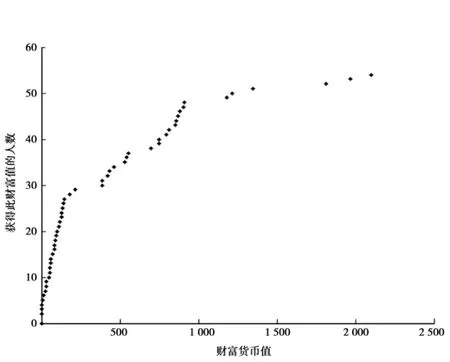
图4 交易规则二下随机模拟人数与货币值对应分布

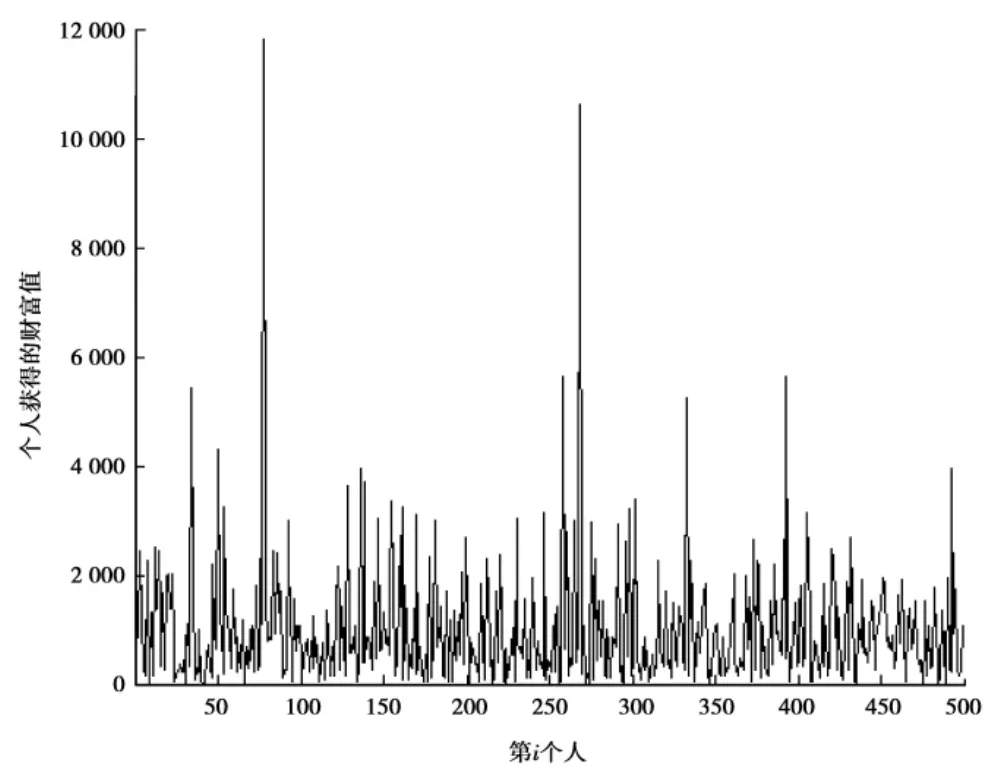
图5 改进后个人货币随机分布

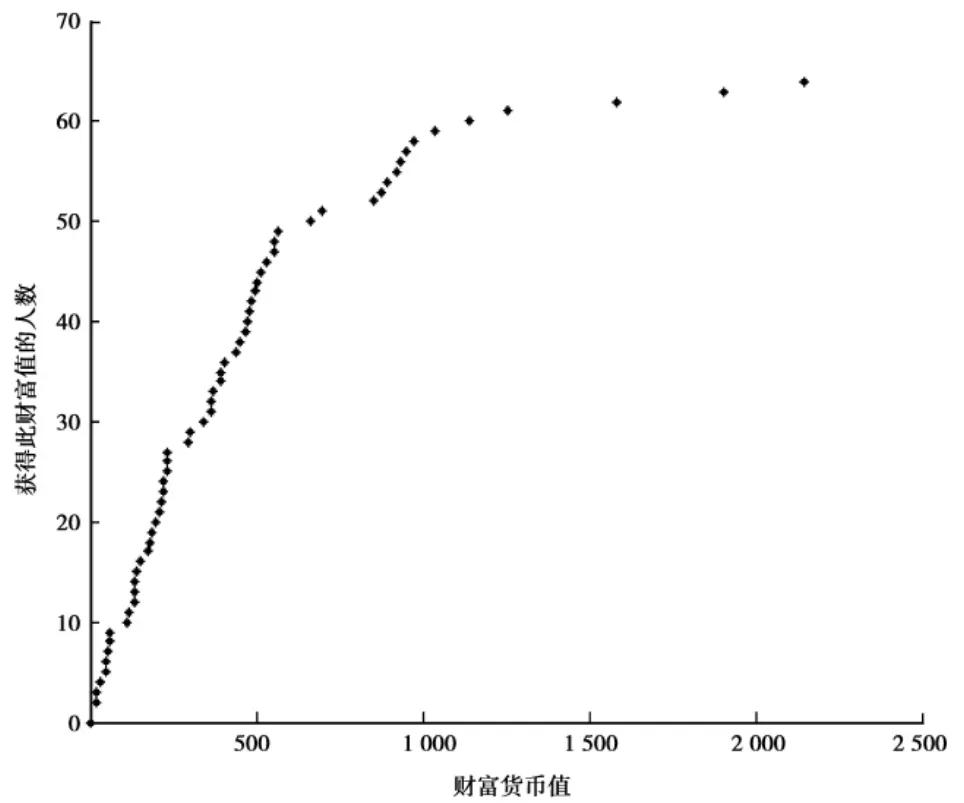
图6 改进后的财富人数随机分布

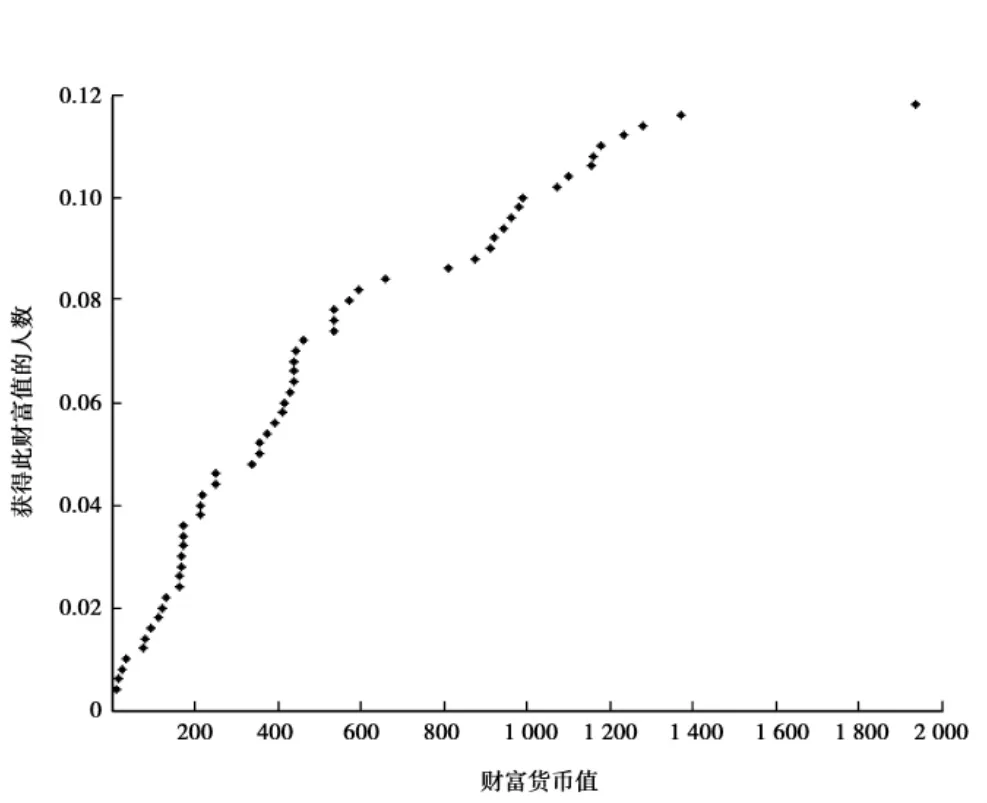
图7 财富值概率对应分布

观察图(5)、(6)、(7)可以发现极少数人获得了大量的货币。系统中的货币分布状况不均衡，基尼系数G=0．506 2，与在模型改良前的基尼系数十分相近，但是更趋近于理论值0．5，而且更符合帕累托定律给出的财富分布状况。由于在改良的过程中引入了更多的因素，因此经过改良后的模型更具实践价值和扩展性。

6 模型的推广与实用性

在模型中，首先忽略了现实生活中随着时间的推移社会生产力的发展，社会总财富与使用货币量的不断增加，忽略了社会生活中复杂的经济交易方式，没有考虑人口的变化情况，仅仅基于一种理想的状态，系统人口数是恒定的。而现实情况下人口的变化是受到许多因素的影响的。虽然建立的模型不适应复杂的经济活动，但是在一个相对短的时间里，可以将社会财富和货币量看作没有改变，而且对那些经济欠发达、缺乏复杂的经济活动地区，则可以忽略其他因素对交易的影响。最后就是在一个相对短的时间里人口的变化极小，于是也可以将人口看做恒定的。因此所建立的模型在局部经济活动中具有一定的实践意义。

参考文献:

［1］张彧杰.带回扣的财富分布模型［J］.大连理工大学学报，2008(2):78-81

［2］CHATTERJEE A，YARLAGADDA S，CHAKRABARTI B.Econophysics of Wealth Distributions［J］.Springer Verlag Milan，2005，17:167-169

［3］GIBRAT R.Les Inegalims Economiques［M］.Paris:1931

［4］DRAGULESCU A，YAKOVENKO V M.Statistical Mechanics of Money［J］.Eur Phys J，2000，17:723-729

［5］陈守洁，凌复华.大自然分守几何学［M］.上海:上海远东出版社，1998

［6］崔卫国.经济模型浅说［M］.北京:经济管理出版社，1988

［7］赵勇，王劲峰.经济分析CGE模型与应用［M］.中国:经济出版，2008

［8］罗斯，斯塔尔·鲁昌.一般均衡论［M］.上海:上海财经大学出版社，2003

［9］程守洙，江之永.普通物理学［M］.北京:高等教育出版社，2008

［10］唐俊波.FDI对中国经济增长影响的实证研究［J］.重庆工商大学学报:自然科学版，2013(2):21-25

Analysis of Monetary Distribution Situation in Closed System

CAO Mao
(School of Mathematics，Chongqing Normal University，Chongqing 401331，China)

Based on individual monetary transfer，the model studies the monetary distribution situation by the molecular movement approximate to analogical thermodynamics.The probability occurred from a state in thermodynamics was pointed out by Blotzmann and Gibbs in reference［1］，and monetary distribution situation is measured by transaction rule made by Gini coefficient.In order to further fit for the practice，the author modified the model，introduced probability r successful in every transaction，where r is randomly generated by the action of some affecting factors in the transaction process，as a result，the model is more valid after analysis.

monetary distribution;transaction rule;Gini coefficient;Pareto Law

O210

A

1672-058X(2014)01-0001-07

责任编辑:田 静

2013-07-28;

2013-08-20.

国家自然科学基金(11001288).

曹茂(1988-)，男，湖北黄冈人，硕士研究生，从事系统理论优化控制方向研究.