消防云梯车变幅液压驱动系统的建模仿真

陈 刚，李 平，崔壮平，曾 杨，蒲鹏飞

（中联重科股份有限公司，湖南 长沙 410013）

1 引言

消防云梯车在高层建筑火灾抢险中担任着非常重要的角色，承担着压制火情、高空抢险、人员施救的重要任务［1－2］，其实车如图1所示.消防云梯车的臂架系统连接在通用汽车底盘基座上，可以完成3个自由度的运动：绕垂直轴线的转动、在垂直平面的升降运动及臂架的伸缩运动，其上车结构示意图如图2所示.图2中，l为臂架长度；θ为臂架变幅角度；φ为臂架回转角度.

图1 消防云梯车实车Fig.1 Fire ladder truck

变幅运动是消防云梯车完成功能的一个主要运动，如果对其实施智能控制，则能显著提高云梯车的工作效率，挽救更多的生命财产［3］.国外已有企业对消防云梯车实施了智能臂架项目，取得了很好的市场反应.获取简单而有效的液压驱动系统模型是实施智能臂架的前提，本文以中联重科的消防云梯车为对象，通过研究分析液压驱动系统中各元件的动静态特性，为消防云梯车臂架的智能控制提供合适的液压驱动系统模型［4－6］.其液压驱动系统如图3所示.图3中，1为具有压力补偿功能的电流比例流量控制阀；2，3为平衡阀；4为单杆活塞缸.平衡阀3是为了使臂架下降时不失速，平衡阀2是为了使臂架停止时不产生向上的过冲.p1为液压缸无杆腔压力；p2为液压缸有杆腔压力；p3为比例阀出油口压力；p4为比例阀回油口压力；A1为液压缸无杆腔有效面积；A2为液压缸有杆腔有效面积；Q1为比例阀出口流量；Q2为比例阀回油口流量.本文利用MATLAB语言中的仿真工具箱——Simulink建立消防云梯车变幅液压驱动系统的仿真模型，研究其运动过程中的动静态特性［7－8］.由于主泵为变量泵，且对于单一的变幅运动，主泵能提供足够的流量，故忽略主泵对液压系统的影响.出于实际应用考虑，本文忽略管道的影响，分别对比例阀、平衡阀和液压缸以及油缸与云梯铰接处建立模型，并与实车测试结果对比，以验证模型的正确性.

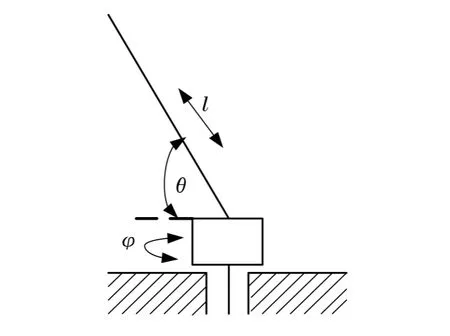
图2 消防云梯车上车结构示意图Fig.2 Fire ladder truck on the car′s structure diagram

图3 消防云梯车的变幅液压驱动系统Fig.3 Fire ladder truck’s hom hydraulic drive system

2 变幅液压驱动系统的建模与仿真

液压缸为单杆活塞缸，结构上的不对称直接导致了其变幅上升和变幅下降时对应的数学模型不同；平衡阀正反向工作时，其工作机理也不一样；为了匹配液压缸和平衡阀，比例阀的机械限位在变幅上升和变幅下降时也是不一样的.因此，需对变幅上升和变幅下降分别建立数学模型.由于变幅上升和变幅下降模型的不同仅仅体现在参数设置上，故本文仅针对变幅上升模型给出详细推导过程.

2.1 比例阀的建模

当比例阀阀芯的运动方向如图4所示时，比例阀进油口的流量q1由伯努利方程可得：

式中：cd为电液比例方向阀的流量系数；ω为阀口的面积梯度；xv为电液比例方向阀的阀芯位移；ρ为液压油的密度；ps为电液比例阀进口压力.

图4 阀控缸的结构简图Fig.4 Cylinder valve control structure diagram

图4中，q2为比例阀的回油流量；FL为负载所受外力；BP为油缸与负载连接处的黏性阻厄系数。

流量方程为非线性的，对式（1）进行线性化，在原点附件对式（1）进行泰勒展开，由于阀芯在原点附件运动，故高阶无穷小可忽略，对流量方程线性化可得：

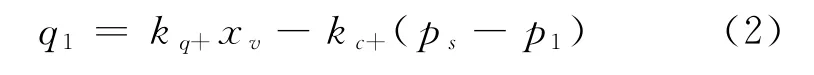
对于消防云梯车使用的多路阀，其（ps－p1）为一定值，由于阀芯位移为零时，其流量也为零，故可得：

而从稳态特性考虑，比例阀的输入电流与阀芯位移是成正比的，即：

式中：K2为比例阀的流量电流增益.

故：

式中：K3＝K1K2，K1为比例阀电控系统的增益.

故从稳态特性考虑，比例阀的输出流量是与输入电流成正比的.

在工程应用中，一般将比例流量阀的动态响应看成一个二阶环节，即：

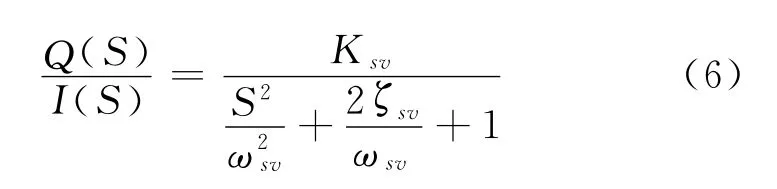
式中：Ksv为电液比例方向阀的流量增益；ωsv为电液比例方向阀的固有频率；ζsv为电液比例方向阀的阻尼比；S为时间变量；Q为比例阀输出流量；I为比例阀输入电流.

2.2 液压缸的建模

液压缸作为功率转换元件，其本身的机能是由一系列功率转换环节组成的，如图5所示，液压缸可看成由4大模块组成.

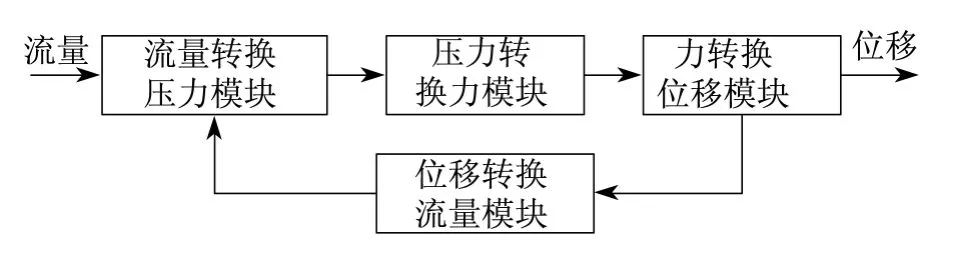
图5 液压缸的功率转换模块Fig.5 Cylinder power conversion module

（1）流量转换压力模块 当来自于阀的流量流入液压缸时，由流量方程可得：

式中：Cip为液压缸内泄系数；Cep为液压缸外泄系数；βe为有效体积弹性模量；V1为液压缸无杆腔体积；t为时间.

可以看出，流入液压缸的流量有4个用途，内泄、外泄、油液压缩产生压力以及活塞运动的消耗.实车测试的结果表明，液压缸的内泄、外泄都可以忽略，即

则流量转换压力模块可表示为

（2）压力转换力模块 流体的压力p作用在液压缸活塞的端面A上，即可以产生与之成比例的力F，因此，压力力转换模块可表示为

（3）力转换位移模块 液压缸与负载的连接可等效为一个质量弹簧系统，由牛顿定律可得液压缸与负载的受力方程：

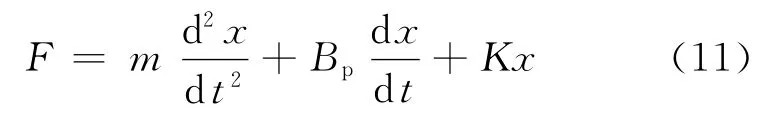
式中：m为活塞及负载总质量；K为负载弹簧刚度.

则力转换位移模块可表示为

（4）位移转换流量模块 活塞的运动会引起流量的变化，则位移转换流量模块可表示为：

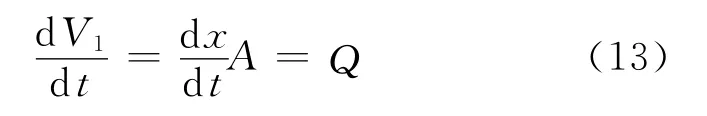
即

2.3 平衡阀的建模

由图6所示可知，平衡阀可看成是由单向阀和液控溢流阀并联组成的.当臂架上升时，3平衡阀的单向阀工作，其流量与压差的关系由阀样本曲线给出，如图7所示，为一个二次函数曲线，即

式中：Δp为平衡阀两端压差；K4为平衡阀的压差流量系数.

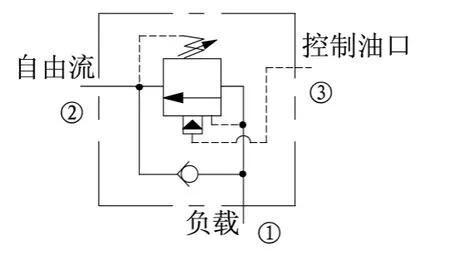
图6 平衡阀的图形符号Fig.6 Valves graphics accord

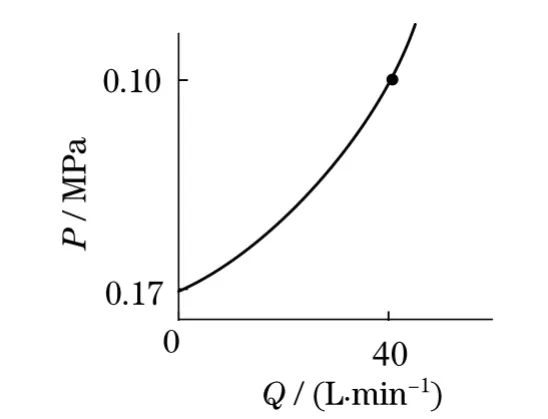
图7 单向阀工作时压差与流量关系Fig.7 Relationship between pressure and flow check valve work

当臂架下降时，3平衡阀的液控溢流阀工作，为了使重物受控下降，平衡阀会维持两个平衡：力平衡和速度平衡（流量平衡）.图8为平衡阀的结构示意图，此时溢流阀开始工作.溢流阀阀芯的开启条件：

式中：A3为控制油口对应阀芯面积；A4为进油口对应阀芯面积；Ki为导压比，取1.5；Fg为弹簧力.

当溢流阀稳态工作时，阀芯上稳态液动力Fy为

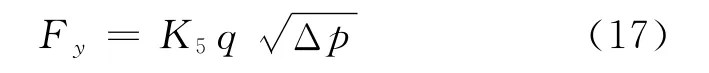
式中：K5为比例系数.

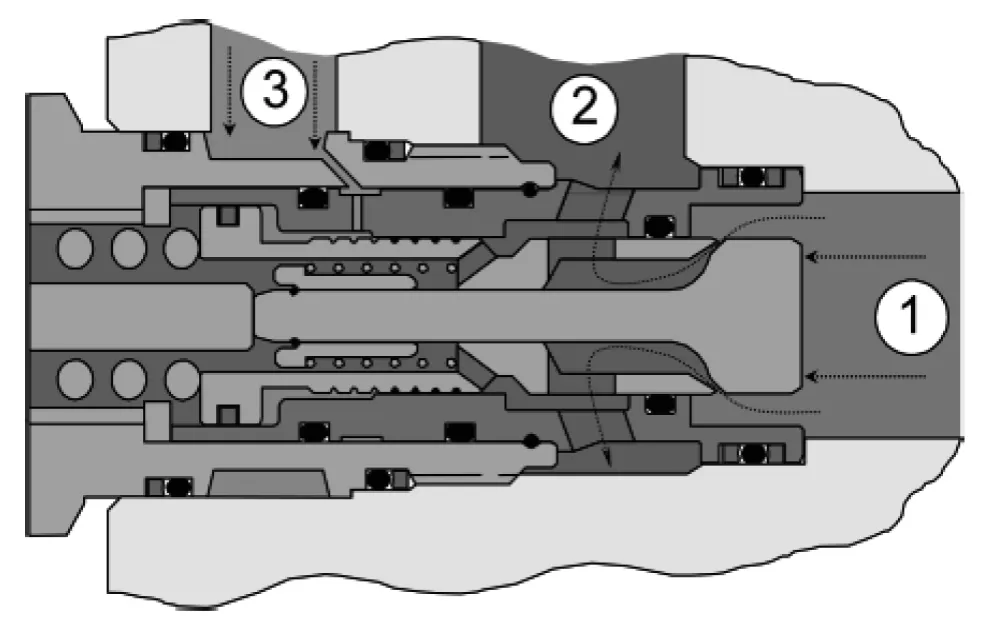
图8 平衡阀的结构示意图Fig.8 Shematic balancing valve

当2口的压力看成零时，就有Δp＝p1.

稳态液动力的方向是使阀芯关闭，则阀芯上的受力方程：

则可得平衡阀稳态时其流量与压差的关系：

由于平衡阀的响应时间要比比例阀快很多，故在此液压系统中，不需要考虑其动态特性.但考虑到无论是单向阀还是液控溢流阀的开启，都会有一个时间延迟过程，故需把该时间延迟叠加到模型中.

2.4 油缸与臂架连接处建模

臂架的变幅角度直接影响臂架自重对液压系统产生的压力，因此需把臂架自重产生的压力变化引入到液压系统中.图9为油缸与云梯臂架的铰接模型图，将其简化为图10所示的三角形.图10中，φa为变幅角度；a为对应的油缸长度；b为油缸底座到臂架底座的长度；c为臂架底座到油缸连接处的长度.

图9 油缸与臂架铰接处Fig.9 Articulated boom cylinder

图10 云梯油缸铰接处三角形Fig.10 Hinged at the triangle ladder cylinders

由三角形关系可得：

式中：vy为油缸的速度.

可得油缸与臂架连接处的模型方程如图11所示.

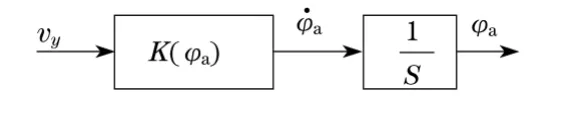
图11 油缸与比较连接处的模型Fig.11 Cylinder modul and compare junction

2.5 模型关键参数的获取

为了获得比例阀的动态响应参数，需对阀进行阶跃响应试验，通过比例阀的阶跃响应曲线，如图12所示，我们可以得出超调量σp和过渡过程时间ts，当0＜ζ＜0.9（ζ为系统阻尼）时，且取误差带Δ＝2%，通过式（22），（23）可获得比例阀的固有频率ωsv和阻尼比ζsv.流量增益由稳态特性可得出.通过实车测试，模型中需确定的参数如表1所示.

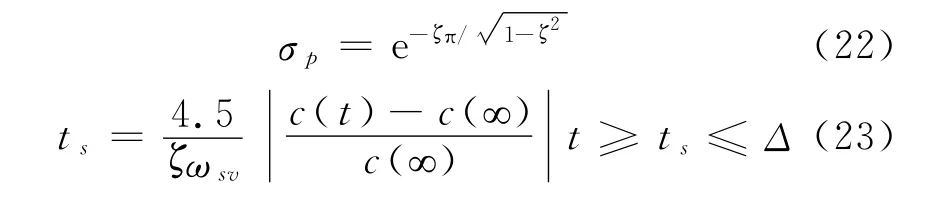
式中：c（t）为比例阀的瞬时输出；c（∞）为比例阀的稳态输出.

2.6 液压驱动系统的仿真与结果对比

设定云梯车为空载，通过上述比例阀、液压缸、平衡阀、油缸与云梯铰接处的建模研究，可得液压驱动系统的Simulink仿真模型如图13所示.

对模型给定阶跃信号，图14为比例阀模型的阶跃响应，由此可知，比例阀的上升时间为86ms，超调量为15%，稳定输出流量20L·min－1.通过实车测试，绘制出的比例阀阶跃响应如图15所示，可计算出，实际比例阀的上升时间为82ms，超调量为12%，稳定输出流量19.4L·min－1.通过比较比例阀模型与实际比例阀的动静态特性指标，可以得出，比例阀模型能较好地反映实际比例阀的动静态特性.图16为液压驱动系统模型在阶跃信号作用下的液压缸位移输出曲线，可以得出，液压系统模型的整个时延大约在0.6s，在启动和制动时，位移输出平缓，速度稳定在0.016m·s－1.通过实车测试，绘制出油缸的位移输出曲线，如图17所示，可得实际液压系统的时延也大约为0.6s，速度稳定在0.015 8m·s－1.仿真模型和实车测试结果具体指标对比见表2.通过对比例阀的动静态特性以及整个液压系统的特性指标进行对比，可以得出，变幅液压驱动系统的Simulink模型较好地吻合实车液压系统.

图12 比例阀关键参数的获取Fig.12 Getting key parameters of proportional valve

表1 模型中的参数Tab.1 Model parameters

图13 液压驱动系统的Simulink仿真模型Fig.13 Simulink simulation model of the hydraulic drive system

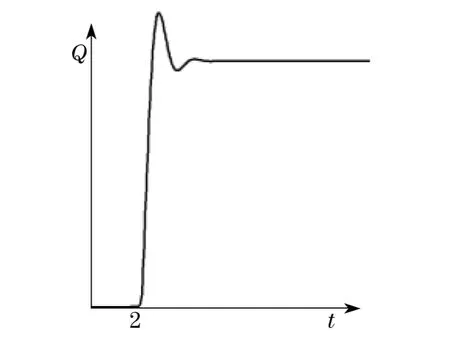
图14 比例阀模型的阶跃响应Fig.14 Step response of proportimal valve model

图15 实际比例阀的阶跃响应Fig.15 Actual step response proportional valve

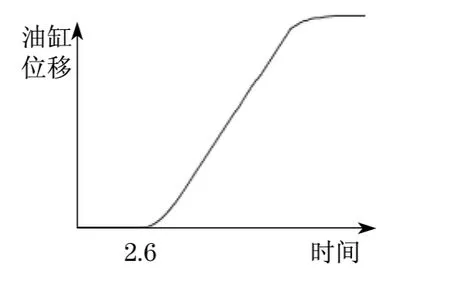
图16 模型的液压缸位移输出曲线Fig.16 Hydraulic cylinder displacement output

表2 结果对比Tab.2 Results contrast

3 结论

简单有效的液压驱动系统模型，是实现臂架变幅运动智能化的前提.通过对液压系统及其元件动静态特性的研究，得出了整个液压系统的Simulink模型.把比例阀的动态特性看成一个二阶环节，把液压缸看成4个不同的功率转换模块，由于平衡阀的响应比比例阀快很多，故忽略了平衡阀的动态特性，通过阀芯稳态受力方程得出了平衡阀的稳态特性.相比于通过阀芯的运动方程建立的模型更加简单，且动静态特性指标能较好地符合实际工况，故更适合作为智能化控制的模型.

［1］吴根茂，邱敏秀，王庆丰，等.新编实用电液比例技术［M］.杭州：浙江大学出版社，2009.WU Genmao，QIU Minxiu，WANG Qingfeng，et al.New practical electro－hydraulic proportional technology ［M ］.Hangzhou：Zhejiang University Press，2009.

［2］梅晓榕，庄显义.自动控制原理［M］.北京：科学出版社，2006.MEI Xiaorong，ZHUANG Xianyi.Principles of automatic control［M］.Beijing：Science Press，2006.

［3］王正林，王胜开，陈国顺，等.MATLAB／Simulink与控制系统仿真［M］.北京：电子工业出版社，2012.WANG Zhenglin，WANG Shengkai，CHEN Guoshun，et al.MATLAB／Simulink simulation and control system ［M］.Beijing：Publishing House of Electronics Industry，2012.

［4］王东，黄效国，郭跃.基于MATLAB／SIMULINK的阀控缸模块化建模与研究［J］.机床与液压，2009（9）：2－3.WANG Dong，HUANG Xiaoguo，GUO Yao.Cylinder valve control based MATLAB／SIMULINK modular modeling and research［J］.Machine Tool ＆ Hydraulics，2009（9）：2－3.

［5］刘宝杰，张保民，权辉.电液比例位置控制系统建模与仿真［J］.液压气动与密封，2011（11）：2－3.LIU Baojie，ZHANG Baomin，QUAN Hui.Electro－hydraulic proportional position control system modeling and simulation［J］.Hydraulic and Pneumatic Seals，2011（11）：2－3.

［6］常珏，冯永宝.电液比例阀控缸速度控制系统的建模与仿真［J］.液压气动与密封，2011（8）：3－4.CHANG Jue，FENG Yongbao.Modeling and simulation of electro－hydraulic proportional valve cylinder speed control system［J］.Hydraulic and Pneumatic Seals，2011（8）：3－4.

［7］姚平喜，张恒，王伟.负载敏感平衡阀动态特性仿真及参数优化研究［J］.机床与液压，2011（7）：3－4.YAO Pingxi，ZHANG Heng，WANG Wei.Load balancing valve sensitive dynamic simulation and parameter optimization［J］.Machine Tool ＆ Hydraulics，2011（7）：3－4.

［8］仇文宁，杜长龙，魏宏宇.基于MATLAB的混凝土输送泵闭式泵送系统建模与仿真［J］.机床与液压，2011，19：1－2.QIU Wenning，DU Changlong，WEI Hongyu.MATLAB－based modeling and simulation of concrete pump closed pumping system［J］.Machine Tool ＆ Hydraulics，2011，19：1－2.