动力平板车车架结构的拓扑优化设计

刘 宇，张生芳，宋雪萍，丁江民

（大连交通大学 机械工程学院，辽宁 大连 116028）

重型动力平板车是额定载重在50t以上的特大、特重货物陆路运输的必备设备，具有自行走功能及液压提升系统，并且有超重载荷搬运、机动灵活、自行驶、高稳定性以及高通过性等优异性能，广泛应用于路桥施工、船舶建造、大型构件整体运输等工程领域［1］.目前，在国际著名的平板车制造商及其研发团队（如德国的KAMAG公司、SCHEUERLE公司，法国的Nicolas公司，日本的Shinko公司以及意大利的COMETTO公司）的引领下，动力平板车正向着大吨位、轻自重的方向发展.KAMAG公司目前最大单台平板车的吨位已达到1 300多吨［2］.尽管我国也能自行研制出吨位接近1 000t的动力平板车，但由于设计理念的落后和缺乏关键技术的掌握，国产平板车在总体结构、转向、行走系统、液压系统等核心部分的设计与制造方面与国外同类相比还有较大差距.在传统设计中常常以经验和使用情况为参照，这样难免会出现产品结构的不合理，进而导致产品的超重，不利于现代产品节能降耗的要求.对于平板车的核心结构件——车架来说，其重量的大小显著影响了平板车的整车自重.如果能够通过结构优化实现车架的减重，则不仅节约了原材料，降低了生产成本，而且车辆工作中降低了燃油消耗，减少了排放，有利于环保，将产生很大的经济与社会效益.因此车架结构的合理设计是重型平板车设计当中至关重要的一步.本文通过对平板车车架结构的拓扑优化分析，提出动力平板车车架的设计方案，为车架的改进设计提供了理论依据.

1 动力平板车的工况分析及建模

1.1 动力平板车的工况分析

图1为动力平板车满载时的工作照片，载荷的重力几乎完全作用在平板车车架上，并由车架传递到下车悬挂系统.就载荷性质而言，车架所受到的主要载荷为弯曲、扭转、偏置和集中载荷等.弯曲载荷是车架自身质量和负载产生的载荷.集中载荷是由于质量比较大的货物集中放在某处所产生的载荷.对载荷处理时，车架自身重量可以通过施加垂直方向上的重力加速度进行等效，货物载荷一般处理为均布载荷.

1.2 建模注意问题

采用HyperWorks软件建模及求解流程如图2所示.

图1 动力平板车满载工作照片Fig.1 Working photo of a fully loaded power platform transporter

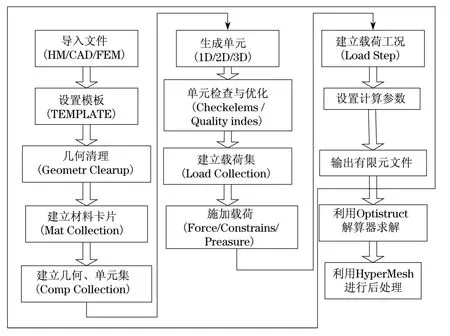
图2 HyperWorks建模流程Fig.2 The modeling procedure of HyperWorks

HyperWorks进行有限元建模时应注意的问题：

（1）导入CAD几何模型时，需要考虑模型规模的大小.对于像车架构件这样结构复杂的大型项目，可在模型导入前去掉对分析结果影响较小的部分零件，并对一些复杂结构进行简化处理，忽略对整体力学性能影响较小的几何细节，如半径为5mm以下的孔、过渡圆角或倒角以及2mm以下的搭接边上的凸台等.

（2）从CAD导入的曲面模型或抽取的中面往往存在缝隙、重叠、错位等缺陷，则需要利用HyperWorks的“Geometry Cleanup”（几何清理）功能来消除错位和小孔，压缩相邻曲面之间的边界，消除不必要细节，以提高整个划分网格的速度和质量，减少计算误差.

（3）有限元网格剖分时，应根据分析的目的并结合模型的特点，选择适当的单元类型，并根据计算机的能力和要求的精度确定合适的网格大小，划分网格.

（4）单元质量对有限元的计算结果有较大影响.应检查所划分的网格单元是否有重复的节点、重复的或缺少的单元以及高度畸变或翘曲的单元.控制单元长宽比≤10，单元内角≥30°，单元翘曲角≤20°并避免特别小的单元［3］.在使用RBE2单元时，须分清主次，即同一个节点只能从属于一个主点.

在模型离散化后，采用HyperWorks中的OptiStruct软件进行拓扑优化求解，OptiStruct求解器采用变密度拓扑优化方法来定义材料流动规律［4］，用近似法和可靠的优化方法搜索得到最优的加载路径设计方案.

2 动力平板车车架拓扑优化分析

2.1 动力平板车车架拓扑优化问题的阐述

在动力平板车车架的设计中，在保证车架强度的同时，减轻车架重量，在保证车架局部屈曲稳定性的前提下，提高车架的刚度一直是人们十分关注的问题.以动力平板车的柔顺性最小为目标，以材料在截面上的分布形式为设计变量，进行拓扑优化分析，从而确定车架的最优结构形式.根据通常的拓扑优化思想，将车架的初始设计区域离散成有限元网格，每个单元内的材料认为是由实体材料和孔洞构成的空心材料，空心材料的等效性质取决于材料的密度或空心率［5］.通过设计各单元的密度实现车架结构的拓扑形式优化.

2.2 动力平板车车架拓扑模型的建立

2.2.1 分析模型选取

平板车车架选择拓扑优化分析时，先可视车架为矩形实体单元，给出模糊轮廓，车架与悬挂连接的回转支承处布置是固定的，所以在相应位置采用刚性单元模拟.

2.2.2 模型的建立

（1）利用HyperMesh软件建立车架实体模型，并加载OptiStruct模板.

（2）创建材料属性，并将其属性分配给各组件集合器.设置初始弹性模量为E＝200GPa，泊松比为μ＝0.3.

（3）在2D组件内创建一层壳单元，用“linear solid”面板创建实体单元.利用“solid map”面板将现有的二维有限元网格拉伸成实体单元网格［6］.

（4）在回转支承位置创建rigidlinks单元.

2.2.3 边界条件的确定

100t动力平板车在工作过程中主要工况分为：①100t均布载荷工况；②100t均布载荷，前轮悬空工况；③100t均布载荷，后轮悬空工况.

对于第1种工况，边界条件是将z方向的位移约束施加在8个回转支承的刚性节点上，均布载荷施加在两侧主梁的节点上.

对于后2种工况，可归纳为3支点工况，即将其中位置相近的两个回转支承点的所有约束放开，其他6个回转支承的刚性节点约束z方向的位移.

2.2.4 拓扑优化设置

（1）优化参数的设置 设计目标：柔度最小；约束：体积分数的上限值为0.15.

（2）定义两个响应 在“responses”子面板中定义 “volumefrac”和 “wcomp”两个响应［7］.选择“Objective”面板将响应“wcomp”定义成目标函数；选择“dconstraints”面板将响应“volume－frac”定义成约束条件.

2.2.5 求解

采用变密度法，通过OptiStruct的拓扑优化模块进行求解.为了消除拓扑优化数值计算中的棋盘格和网格依赖现象，惩罚因子p取为3.优化结果如图3—6所示，其中图3为车架在工况1载荷情况下的3D拓扑优化图.

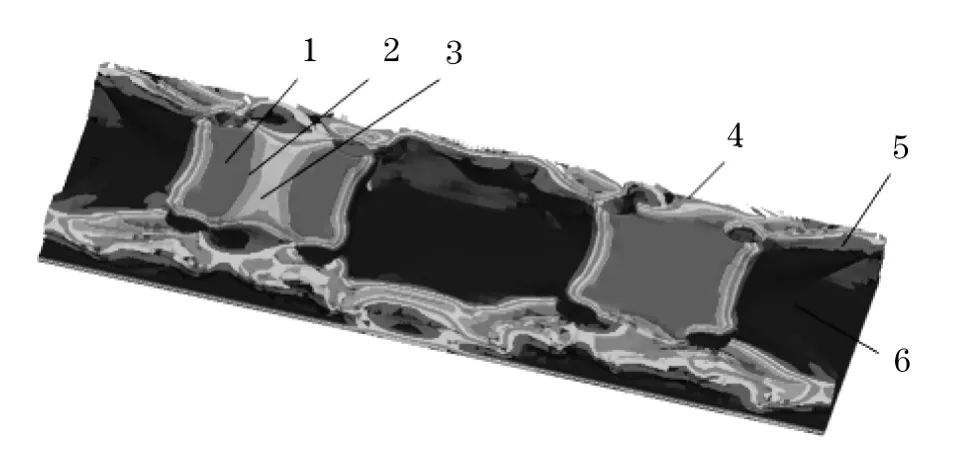
图3 工况1车架3D拓扑优化图Fig.3 3Dtopology optimal diagram of frame in case 1

图4 工况1车架主平面拓扑优化图Fig.4 Main plane of frame topology optimal diagram in case 1

图5 工况1车架侧平面拓扑优化图Fig.5 Side plane of frame topology optimal diagram in case 1

图6 工况2车架主平面拓扑优化图Fig.6 Main plane of frame topology optimal diagram in case 2

3 拓扑优化结果分析

在图3—6所获得的车架拓扑图形中，不同颜色的区域代表不同的密度分布，具体数值见表1.相对密度值最大的区域是1区，代表主要承受载荷的区域.2—6区相对密度依次减少，说明所承受的载荷也依次减小，特别是5，6区，相对密度小于0.434，这部分所承受的载荷很小，在设计时可考虑将材料去除.

表1 相对密度分布表Tab.1 Distribution table of relative density

工况1下的车架主平面拓扑图如图4所示.1区主要分布在上下相对应的回转支承之间的连接区域以及施加载荷的上下两个边缘处，因此在1区相应位置添加主要承力材料，在设计时可以考虑把主梁安放在此位置.2—4区域主要分布在1区附近，区域的分布走势基本与1区相同，为次要承力部分，此部分可适当布置承力材料，如布置加强梁和加强筋板等.5、6区基本分布在中间两轴之间、前后两轴与车架前后沿之间除去两侧边缘的中间大块区域，此部分的密度值很低，可视为无材料区，设计时可考虑掏空或仅布置少量材料起连接作用.

工况1下的车架侧平面拓扑图如图5所示.从图5可以看出，在工况1的载荷情况下，侧平面的主要承载区域1区分布在图形的中间部位，并几乎占据了侧平面的整个高度范围.在中间的两侧，1区所占比例骤然减小，约占整个高度的1／3.参考图3的拓扑图形，可知侧平面所描绘的1区域应位于车架的上下两侧，可在此位置布置主要承力的梁结构，并结合1区域在图5中的分布走势，将梁的侧截面设置成两边低、中间高的倒置梯形结构.此外，在侧平面拓扑图的两端1区域所占比例又迅速升高，约占1／2高度范围，则可考虑在车架的前后两端增加端梁结构以改善车架的受力.

工况2下的车架主平面拓扑图如图6所示.1区主要分布在回转支承附近，因此，在回转支承位置处应主要布置承力材料，这一点与工况1的部分分析结果相类似.2区主要分布于回转支承交叉连接的区域之间，可根据实际情况设置加强梁（尤其当车架的中间两轴间距较大时），以抵抗由载荷偏置而造成的车架的侧扭.图6中其余大部分位置的相对密度都比较小，在设计中可适当略去材料的布置.

4 结论

本文利用HyperMesh软件中Optistruct模块对100t动力平板车车架结构进行拓扑优化分析，根据优化结果获得了实际工况下车架的承载规律，并结合车架拓扑优化分析结果，给出了动力平板车车架材料布置形式的建议，为车架的轻量化设计提供了理论依据.

［1］王智勇，赵静一，张齐生.负荷传感技术在重型平板车液压控制系统上的应用［J］.中国工程机械学报，2005，3（4）：435－438.WANG Zhiyong，ZHAO Jingyi，ZHANG Qisheng.Application of load sensing technology in the hydraulic control system of heavy duty transporter［J］.Chinese Journal of Construction Machinery，2005，3（4）：435－438.

［2］王欣，张明辉，高顺德等.大型动力平板车技术的发展［J］.工程机械与维修，2006，8（12）：81－83.WANG Xin，ZHANG Minghui，GAO Shunde，et al.The development of heavy power platform transporter technology［J］.Construction Machinery ＆ Maintenance，2006，8（12）：81－83.

［3］王钰栋，金磊，洪清泉，等.Hyper Mesh ＆ Hyper View应用技巧与高级实例［M］.北京：机械工业出版社，2013.WANG Yudong，JIN Lei，HONG Qingquan，et al.Hyper Mesh ＆ Hyper View application techniques and advanced examples［M］.Beijing：China Machine Press，2013.

［4］陈敏志，张旭明，徐冯君.拓扑优化研究方法综述［J］.山西建筑，2005，31（21）：63－64.CHEN Minzhi，ZHANG Xuming，XU Fengjun.A review on topology optimization methods［J］.Shanxi Architecture，2005，31（21）：63－64.

［5］BENDSOE M P，RODRIGUES H C.Integrated topology and boundary shape Optimization of 2－D solids［J］.Computer Methods in Applied Mechanics and Engineering，1991，87（1）：15－34.

［6］于开平，周传月，谭惠丰，等.Hyper Mesh基础培训教程［M］.北京：科学出版社，2005.YU Kaiping，ZHOU Chuanyue，TAN Huifeng，et al.Hyper mesh basic training［M］.Beijing：Science Press，2005.

［7］王欣，黄琳，高媛等.起重机伸缩臂截面拓扑化探析［J］.中国工程机械学报，2007，5（3）：288－292.WANG Xin，HUANG Lin，GAO Yuan，et al.Investigation into topological optimization for telescopic boom sections of cranes［J］.Chinese Journal of Construction Machinery，2007，5（3）：288－292.