电动助力转向系统参数研究及优化设计

王 伟，云 浩

（福州大学 机械工程及自动化学院，福建 福州 350108）

随着汽车速度的不断提高，人们对电动助力转向系统转向性能的要求也越来越高.转向路感是输出端的变化引起的输入端的变化，反映的是转向系统的逆效率；转向灵敏度是输入端的变化引起的输出端的变化，反映的是转向系统的正效率.因此，转向路感和转向灵敏度之间存在一定的耦合性.已有的研究在转向参数影响和性能优化方面做出了一定的贡献，但较少文献考虑了转向路感和转向灵敏度之间的耦合作用.陈慧鹏等［1］将转向路感作为单一优化目标，忽略了转向系统结构参数对转向灵敏度的影响，在优化了路感的同时难以保证灵敏度的要求.陈龙等［2］分析了EPS系统主要参数对整车性能的影响以及匹配性关系，而对转向系统自身转向性能的影响却未进行分析.崔晓利等［3］考虑了EPS系统结构参数对转向性能的影响，并对其进行了优化设计，但控制参数的影响并未得到研究.

本文建立了集成整车的EPS系统动力学模型，对转向路感、转向灵敏度和转向稳定性进行了理论分析和量化处理，并研究了EPS系统结构与控制参数对转向性能指标的影响.此外，本文建立了以转向稳定性为约束条件，以转向路感、转向灵敏度有效频域能量均值为目标函数的优化设计模型，并利用MATLAB遗传算法（Genetic Algorithm，GA）工具箱对EPS系统的参数进行了优化设计.最后，对优化前后的结果进行了对比分析，验证了优化设计的有效性.

1 动力学模型

1 动力学模型

EPS系统的机械部分主要由方向盘、转向轴、电动机和减速机构组成.根据系统的使用条件和研究对象，对其各部件进行简化，得到简化后的EPS系统动力学模型，如图1所示.

转向系统的动力学方程［4］如下：

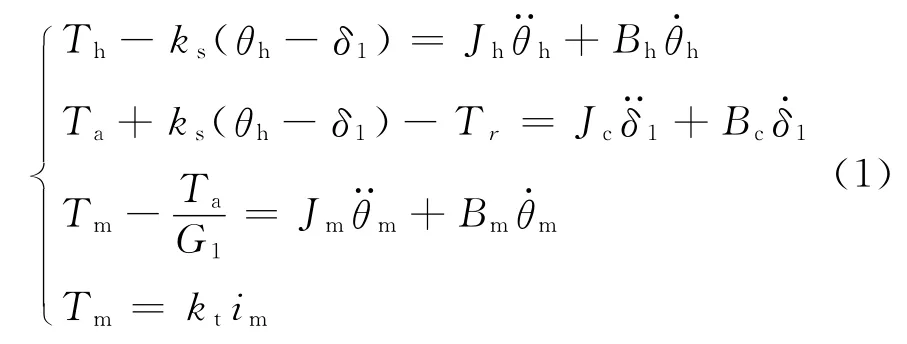
式中：Th为转向扭矩；ks为扭矩传感器刚度；θh为方向盘转角；δ1为输出轴转角；Jh为方向盘的转动惯量；Bh为阻尼系数；Ta为电动机作用到输出轴的助力；Tr为等效到输出轴的转向阻力；Jc，Bc为前轮及转向机构向输出轴等效后的转动惯量和阻尼系数；Tm为电磁转矩；G1为EPS系统从助力电动机到输出轴的传动比；Jm，Bm为电动机的转动惯量和阻尼系数；θm为电动机转角；kt为电动机转矩系数；im为电动机电枢电流.

电动机电气特性方程：

式中：U为电动机电压；R为电动机电枢电阻；L为电动机电枢电感；t为时间；ke为反电动势常数.

电动机、输出轴和前轮的转角关系为

式中：G2为从输出轴到前轮的传动比；δ为前轮转角.

为了使EPS系统能够更好地适应路况，助力电压采用PD（Proportional Derivative）控制器控制，电动机控制器模型为

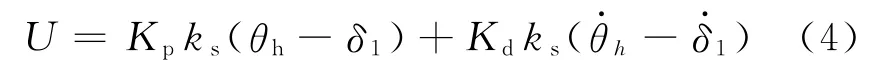
式中：Kp为比例系数；Kd为微分系数.

图1 EPS系统动力学模型Fig.1 EPS system dynamic model

1.2 整车动力学模型

为了研究EPS系统的动态特性及其与整车之间的相互关系，本文采用二自由度汽车动力学模型［5］.整车动力学方程为

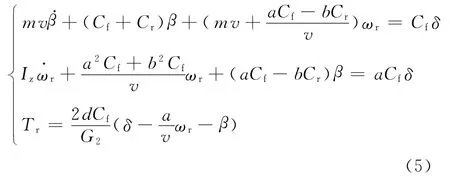
式中：m为整车质量；v为车速；β为质心侧偏角；Cf，Cr分别为前轮和后轮的侧偏刚度；a，b分别是前、后轮到质心的距离；Iz车身横摆转动惯量；ωr为横摆角速度；d为前轮拖距.

对式（5）进行零初始条件的拉普拉斯变换，可得到：

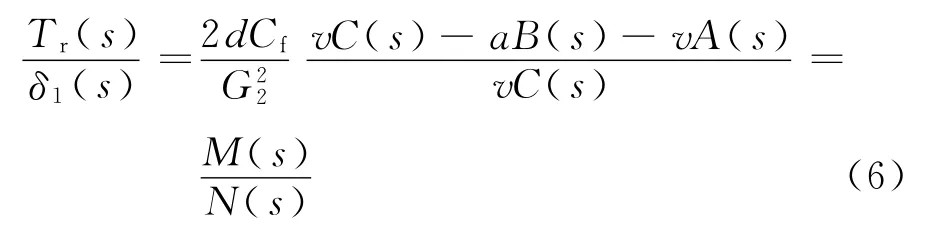
式中：C（s）＝mIzvs2＋［m（a2Cf＋b2Cr）＋Iz（Cf为前后轴的轴距，l＝a＋b；s为函数中的复变数.

2 转向性能评价指标

2.1 转向路感

转向路感定义为保持转向盘转角不变情况下，从车轮负载到所需方向盘转矩的传递函数［6］.根据式（1）—（6），可得转向路感传递函数FS（s）为

式中：Z（s）＝Jss2＋其中，Js＝Jc＋JmG12，Bs＝Bc＋BmG12.

2.2 转向灵敏度

转向灵敏度反映了汽车对转向动作的响应速度，是衡量EPS系统综合稳定性的一个重要指标.本文选取方向盘转角到汽车的横摆角速度的传递函数来表示转向灵敏度.

由式（1）—（6）可得，转向灵敏度函数为ES（s）

式中：X（s）＝ktG1（Kpks＋Kdkss）＋ks（Ls＋ktG1Kpks＋（Kdks＋keG1）ktG1s

2.3 转向稳定性

转向稳定性是指转向系统和整车系统的综合稳定性，必须始终得到保证.而转向稳定性在转向灵敏度函数中得到充分的体现，因而选用灵敏度函数的特征多项式C（s）Y（s）来分析系统的稳定性.

式中：a5＝JsL；a4＝Js（R＋Lg）＋BsL；a3＝Js（Lh＋Rg）＋Bs（R＋Lg）＋（ks＋k）L＋（Kdks＋keG1）ktG1；a2＝JsRh＋Bs（Lh＋Rg）＋ks（R＋Lg）＋kR＋eL＋（Kdks＋keG1）ktG1g＋ktG1Kpks；a1＝BsRh＋ks（Lh＋Rg）＋eR＋Lf＋ktG1Kpksg＋（Kdks＋keG1）ktG1h；a0＝ks（ktKpG1h＋Rh）＋fR；其中，k，e，f，g，h均为表达式化简后的系数.

根据劳斯判据［7］，要使EPS系统稳定，必须满足如下条件：

3 参数研究和优化设计

3.1 EPS系统参数研究

Jm，G1，ks，Kp和Kd是影响转向路感和转向灵敏度的5个重要参数，因而它们与转向性能指标之间的关系需要进一步的研究.根据系统仿真结果，选取电机转动惯量Jm的参数序列为｛0.001，0.006，0.01，0.06｝，传动比G1的参数序列为｛10，20，30，40｝，扭矩传感器刚度ks的参数序列为｛50，100，200，500｝，比例系数Kp的参数序列为｛0.1，0.5，1，5｝，微分系数Kd的参数序列为｛0.01，0.05，0.1，0.5｝.这5个参数与转向性能指标的关系曲线分别如图2—6所示.

由图2和图3可知，随着电机转动惯量Jm和传动比G1的增大，转向路感和转向灵敏度的响应带宽减小，相位滞后，系统延迟增大，从而影响系统的动态性能，并且当Jm取值超过0.01kg·m2后将导致幅频特性曲线振荡并最终失去稳定.

图2 Jm对转向路感和转向灵敏度的影响Fig.2 Effect of Jmon steering feel and steering sensitivity

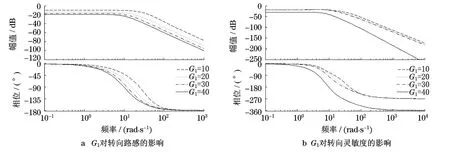
图3 G1对转向路感和转向灵敏度的影响Fig.3 Effect of G1on steering feel and steering sensitivity

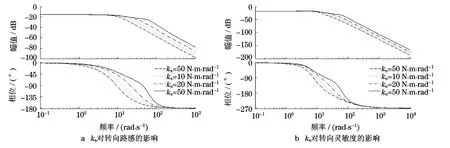
图4 ks对转向路感和转向灵敏度的影响Fig.4 Effect of kson steering feel and steering sensitivity

图5 Kp对转向路感和转向灵敏度的影响Fig.5 Effect of Kpon steering feel and steering sensitivity

从图4可以看出，随着扭矩传感器刚度ks的增大，转向路感和转向灵敏度的响应带宽增大，相位滞后，系统延迟减小.因此，ks应在允许范围内尽可能取较大值.

由图5可知，比例系数Kp对转向灵敏度没有明显影响，随着Kp的增大，转向路感的相位滞后减少而响应带宽减小，并且当Kp取值超过1时，响应带宽明显减小.因此，Kp的取值应适当减小.

从图6可以看出，随着微分系数Kd的增大，转向灵敏度的响应带宽增大，相位滞后减小，而转向路感的响应带宽减小，相位滞后有所增大.

3.2 优化模型设计与计算

在整个路面频率范围中，低频输入是驾驶员转向路感中最主要的构成，而高频成分则代表了路面的噪声信号.在路面信息的有效频率成分范围内，转向路感的频域能量平均值越大越好.转向路感的频域能量均值f1（x）为

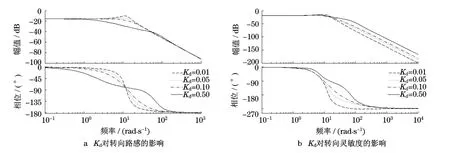
图6 Kd对转向路感和转向灵敏度的影响Fig.6 Effect of Kdon steering feel and steering sensitivity

式中：ω为频率值；ω01为转向路感有用信号的最大频率值.

同理，转向助力必须对驾驶员命令有快速而及时的响应，应使得转向灵敏度的有效频域能量平均值越大越好.转向灵敏度频域能量均值f2（x）为

式中：ω02为转向灵敏度有用信号的最大频率值.根据文献［8］和文献［9］中对有效频率的分析讨论，取其值为ω01＝15Hz，ω02＝5Hz.通过权重系数变化法，将多目标优化问题转化为单目标优化问题.因此，在系统稳定条件下设计的优化数学模型为

式中：g1（x），g2（x），g3（x）是约束条件；X为状态变量；XL和XU分别为X的上、下限.

优化数学模型采用MATLAB遗传算法工具箱求解［10］，遗传进化过程及优化结果如图7所示.从图中可以看出，经过100代进化，目标函数值不断减小，优化前的最佳适应度值为－0.005 2，优化后的最佳适应度值为－0.014 7，是原来的2.83倍，这表明优化后使得转向灵敏度和转向路感的有效频域能量均值得到了提高.各设计变量的初值、上下限和最优值如表1所示.

图7 遗传进化过程Fig.7 Process of genetic evolution

表1 设计变量的初值、上下限和最优值Tab.1 Boundary，initial and optimum values of design variables

4 仿真对比分析

对优化前后的EPS系统进行仿真对比分析，仿真结果如图8—9所示.图8为优化前后的转向路感波得（bode）图.由图可知，优化后的转向路感频率稳定值和响应带宽明显增大，频率响应特性得到改善，而且相位滞后减少，系统延迟较小.图9为优化前后的转向灵敏度bode图.从图中可以看出，优化后的转向灵敏度响应带宽略有增大，相位滞后减少.结果表明：EPS系统参数的优化使系统在满足稳定性的条件下有效地提高了转向路感和转向灵敏度.

图8 优化前后的转向路感对比曲线Fig.8 Contrast curve of steering feel

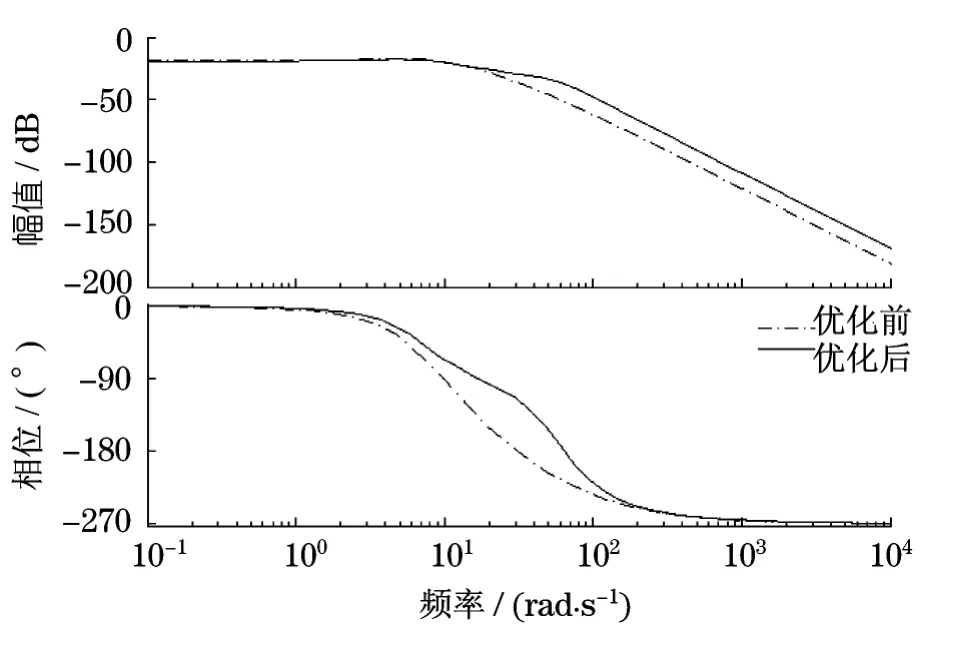
图9 优化前后的转向灵敏度对比曲线Fig.9 Contrast curve of steering sensitivity

5 结论

（1）基于EPS系统与整车的集成模型，给出了转向路感和转向灵敏度计算公式，推导了转向系统稳定性条件方程，为汽车EPS系统转向性能的综合定量评价提供了计算依据.通过频域的仿真计算，得到了EPS系统主要参数与转向路感、转向灵敏度之间的关系曲线.

（2）通过遗传算法对EPS主要参数进行了多目标优化设计，并利用优化后的参数进行仿真验证.结果表明，转向系统性能得到了较大的提高.

［1］陈慧鹏，陈立平，王君明.电动助力转向系统性能优化及参数研究［J］.机械科学与技术，2010，29（2）：146－152.CHEN Huipeng，CHEN Liping，WANG Junming.Optimization of the parameters and performance of an electric power steering system［J］.Mechanical Science and Technology for Aerospace Engineering，2012，29（2）：146－152.

［2］陈龙，毛建伟，江浩斌，等.汽车电动助力转向系统特性及其与整车性能的匹配研究［J］.中国机械工程，2008，19（4）：475－480.CHEN Long，MAO Jianwei，JIANG Haobin，et al.Study on electric power steering characteristics and matching with the whole vehicle［J］.China Mechanical Engineering，2008，19（4）：475－480.

［3］崔晓利，杨岳，毛建伟.汽车电动助力转向系统的匹配分析及优化设计［J］.机械科学与技术，2010，29（1）：1－6.CUI Xiaoli，YANG Yue，MAO Jianwei.Analysis of the matching of an electric power steering system and its optimization design［J］.Mechanical Science and Technology for Aerospace Engineering，2012，29（1）：1－6.

［4］余志生.汽车理论［M］.北京：机械工业出版社，1990.YU Zhisheng.The theory of automobile［M］.Beijing：China Machine Press，1990.

［5］郭孔辉.汽车操纵动力学［M］.长春：吉林科学技术出版社，1991.GUO Konghui.Dynamic of controllability automobile［M］.Changchun：Jilin Science and Technology Press，1991.

［6］CHEN J S.Control of electric power systems［R］.SAE Paper，1998：981116.

［7］林建涛，唐应时，姚汉波，等.电动助力转向系统结构参数优化［J］.计算机仿真，2011，28（11）：297－301.LIN Jiantao，TANG Yingshi，YAO Hanbo，et al.Optimization of electric power－assisted steering parameters on road feel［J］.Computer Simulation，2011，28（11）：297－301.

［8］NOBUO S，YUKIHIRO F，KENKO U，et al.Electric power steering with H－infinity control designed to obtain road information［C］∥Proceedings of the American Control Conference，1997.［s.l.］：American Automatic Control Council，1997：2935－2939.

［9］ALY B，JEFF Z，FARHAD B，et al.Modeling and analysis of an electric power steering system［R］.SAE Paper：1999：1999－01－0399.

［10］雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2011.LEI Yingjie，ZHANG Shanwen，LI Xuwu，et al.MATLAB genetic algorithm toolbox and application［M］.Xian：Xian Electronic Science and Technology University Press，2011.