考虑装配误差的轴系结构静力学对比分析

王宇宁，孙志礼，杨 丽，佟 操

（东北大学 机械工程与自动化学院，辽宁 沈阳 110819）

对于机械传动系统，通过局部分析来评估结构整体的受力分析会产生较大的误差，而航空发动机附件机匣作为复杂传动系统，其包含了很多轴、轴承、齿轮等构件，整个系统的运动状况决定构件内部的运动状态和受力状况，同时也决定其应力应变的分布.若要精确地模拟整个系统的运动，则须对传动系统进行整体分析.但整体结构分析由于规模大、难度高，成为十分迫切与关键的瓶颈问题.国内外很多学者进行了相关研究，张勇等从弯扭耦合振动的角度建立了轴系的数学模型［1］；孙伟等针对高速主轴系统在静止及运转状态下进行了动力学特性对比分析［2］；刘桂珍等考虑油膜力特征对转子－轴承系统进行了非线性动力学研究［3］；LYRIDIS等以船用柴油机的轴系结构为研究对象进行了可靠性分析［4］；LARMI对内燃机轴系的扭振进行了自由振动分析和强迫振动分析［5］.装配误差对轴系传动性能的影响还鲜有报道，而齿轮轴线平行度偏差是装配过程中比较常见的一种情况［6］，因此，通过变换齿轮轴不平行时角度的大小，实现齿轮轴线平行度偏差的变化，应用有限元法对轴系结构进行静力分析，研究齿轮、轴承的应力变化，对于指导传动系统在实际工况中的结构设计具有重要意义.

本文以轴-齿轮-轴承组成的附件机匣传动系统中的轴系结构为研究对象，基于接触问题的求解算法采用ANSYS对轴系结构进行静态仿真，在考虑了装配误差因素的轴线平行度偏差的情况下分别对轴系结构、齿轮和滚动轴承进行静态对比分析.

1 求解接触问题的有限元法

设A1，A2在接触面上的接触对分别为i（1）和i（2），i＝1，2，3，…，r，接触对的柔度方程［7］为

接触边界为

式中：δ0为初始位移向量.

则得到全部接触对的接触方程：

式中：rj为接触点j的接触位移向量；θi为接触点i的转动角；δi为节点i节点引起的外部加载位移向量；Tw施加的外部转矩.

式（3）形成了全部接触对的接触方程，用对称方程组的（Cholesky）分解法进行每次迭代，通过接触状态对接触点对中最大负接触内力进行剔除，形成了新的柔度子矩阵，进行循环迭代求解.

2 轴系结构装配误差的确定

齿轮轴线平行度偏差包括轴线平面内的平行度偏差fδ和垂直平面上的平行度偏差fβ；其中fδ是在两轴线的公共平面上测量的，此公共平面的是用两轴承跨距中较长的一个L和另一根轴上的一个轴承来确定的；而fβ是在与轴线公共平面相垂直的平面上测量的；为了轴线平面内的平行度偏差fδ变化对于轴系结构的影响，将轴线平面内的平行度偏差fδ等效成主动轮心轴由一端面为支点向外扭的角度α，通过改变α的大小研究分析对于轴系结构的影响.

通过轴线平行度偏差的相关资料［8］可知α为0.21°左右，因此，选取理想值0°和可用值0.2°以及可用值之外的角度0.4°，如图1所示，通过改变α角度的大小，使主动轮心轴由一端面为支点向外分别扭转0°，0.2°，0.4°，这样能更利于观察明显的变化结果.

图1 轴线不平行的情形示意图Fig.1 Uneven rows of two－axis diagram of error conditions

3 边界条件和载荷的确定

轴系中的结构件采用的是面－面接触方式，根据目标面和接触面的选择原则建立接触对，齿轮、轴承、轴的接触面和目标面的选择如表1所示.

表1 接触面和目标面Tab.1 Contact surface and target surface

用ANSYS做静态接触时，不允许接触对间有间隙，因此需要打开闭合间隙，同时需要施加初始渗透开关，选择高斯积分节点作为接触监测点.

对于轴系中的齿轮，通过ALL DOF命令约束从动轮全部边界的节点，限制从动齿轮的转动；对主动轮通过DOF约束齿轮轮毂边界主要节点的轴向约束和法向约束，然后在主动轮轮毂边界节点上施加切向力，称为直接施加扭矩；对于轴系中的轴承，将带有轴承的齿轮轴的空心轴两端施加轴向约束，耦合空心轴内圈表面所有节点的自由度，使其在载荷作用下具有相同的位移.将节点坐标系转化到柱坐标系下，施加圆周切线作用力，对另一个齿轮内圈表面全部节点施加全约束［9］.

4 算例

以某轴－齿轮－轴承所组成的附件机匣传动系统的轴系为研究对象，轴承的主要几何参数如表2所示，齿轮的主要几何参数如表3所示，材料的弹性模量为211GPa，泊松比为0.3，齿轮的转矩为210 N·m，轴系的实体模型如图2所示.

表2 深沟球轴承的尺寸Tab.2 Size of the deep groove ball bearings

对于齿轮的网格划分主要采用的是扫掠网格划分，而对于轴承滚动体采用的是映射网格划分的方法，根据表1确定轴系结构中齿轮、轴承的接触对，如图3所示.

当两轴误差倾斜角变化为0°，0.2°，0.4°时，整体轴系结构的静力分析等效应力值如表4所示.图4—8均为应力云图.

表3 齿轮的主要参数Tab.3 Basic parameters of gear

图2 轴系结构实体模型Fig.2 Solid model of shafting structure

图3 接触对的建立Fig.3 Establishment of the contact

表4 随角度变化的整体结构的等效应力值Tab.4 Shafting institutions stress with the change in angle

为了更直观地看出转变角度之后的应力结果变化，选取0°和0.4°的应力云图，如图4所示.对轴系整体结构进行比较时，可以看出，其中在0°时，最大等效应力发生在轴承滚动体上，而在齿轮轴不平行时误差为0.2°到0.4°时，最大等效应力发生在齿轮啮合处，可以说明随着齿轮轴不平行时误差的增加，轴系结构的等效应力大小变化比较明显，尤其对齿轮应力的影响非常明显，因此在以后对轴系结构进行装配时应该严格的控制轴线平行度偏差.

图4 随角度变化的轴系应力云图Fig.4 Shafting structure stress cloud with the change in angle

当两轴误差倾斜角变化为0°，0.2°，0.4°时，齿轮等效应力值如表5所示.选取0°和0.4°的应力云图，如图5所示.

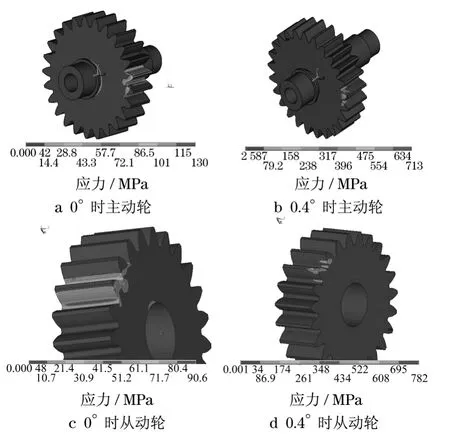
图5 随角度变化的主从动齿轮应力云图Fig 5 Driving and driven gear stress cloud with the change in angle

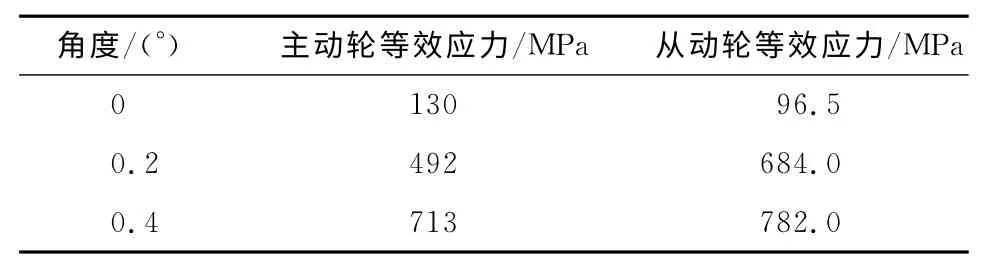
表5 随角度变化的主从动齿轮轴的等效应力值Tab.5 Driving and driven gear stress with the change in angle

通过应力云图5可以看出，齿轮轴不平行时误差为0°时，齿轮在啮合的过程中，应力主要集中在接触部位和齿根部位，并且最大应力发生在齿根部位，轮齿在啮合受载后发生了变形，两个齿轮的接触线为均匀的面接触.

当两轴误差倾斜角变化为0°，0.2°，0.4°时，滚动体的静力分析等效应力值如表6所示.

表6 随角度变化的滚动体的等效应力值Tab.6 Rolling element stress with the change in angle

选取0°和0.4°时的应力云图，如图6所示.

通过图6可以看出，轴承与内外圈接触时，接触区域成椭圆形分布，其长短半轴的偏差也比较明显，这与赫兹接触理论［10］一致；在轴承正下方的滚动体和相接触的内外圈受力最大，即轴承发生破坏时，危险部位即为滚动体与内外圈接触点处.

图6 随角度变化的滚动体应力云图Fig.6 Rolling stress cloud with the change in angle

当两轴误差倾斜角变化为0°，0.2°，0.4°时，轴承内圈的静力分析等效应力值如表7所示.

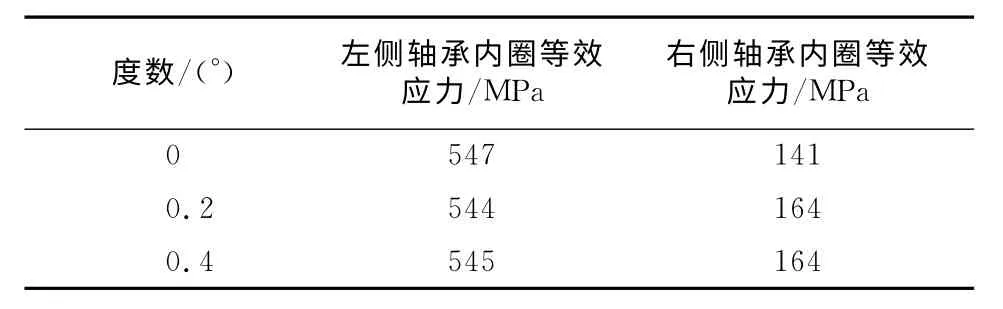
表7 随角度变化的轴承内圈的等效应力值Tab.7 Bearing inner race stress with the change in angle

同样选取0°和0.4°时的应力云图，如图7所示：

图7 随角度变化的轴承内圈应力云图Fig.7 Bearing inner race stress cloud with the change in angle

当两轴误差倾斜角变化为0°，0.2°，0.4°时，轴承外圈的静力分析等效应力值如表8所示.

表8 随角度变化的轴承外圈的等效应力值Tab.8 Bearing outer ring stress with the change in angle

同样选取0°和0.4°时的应力云图，如图8所示.

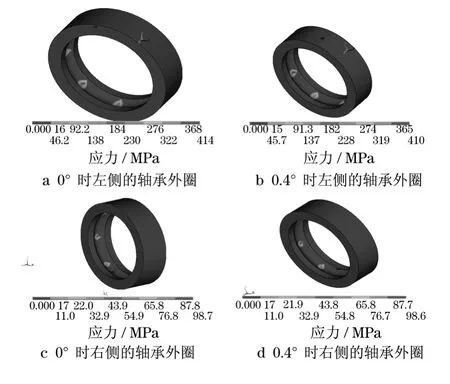
图8 随角度变化的轴承外圈应力云图Fig.8 Bearing outer race stress cloud with the change in angle

当轴系结构在齿轮轴不平行时误差分别为0°，0.2°，0.4°，对滚动轴承来说，从图6—8可以得出，随着齿轮轴不平行时误差的增加，轴承内圈、外圈、滚动体的等效应力变化相对较小，这说明轴不平行时误差的变化对于轴承的应力变化影响较小.这是由于在静力学计算时，随着齿轮轴不平行时误差的增加，主动轮施加给从动轮上的力的总大小是一样的，进而滚动轴承所承受的力是一样的，故而变化较小.

5 结论

（1）齿轮在啮合的过程中在接触部位和齿根部位的的应力的大小受齿轮轴不平行度误差的影响，最大应力发生在齿根部位.

（2）齿轮轴不平行度误差对轴承内圈、外圈、滚动体的等效应力变化相对较小，轴承发生破坏时，危险部位为滚动体与内外圈接触点处.

（3）随着齿轮轴不平行时误差的增加，轴系结构的等效应力相应地增加，且齿轮应力变化较为明显，轴承的应力变化较小.因此在实际装配中，应该严格控制齿轮的装配误差，保证轴系结构的正常运转.

［1］张勇，蒋滋康.轴系弯扭耦合振动的数学模型［J］.清华大学学报：自然科学版，1998，38（8）：114－117.ZHANG Yong，JIANG Zikang.Mathematic model of coupled bending and torsional vibration of shaft systems［J］.Journal of Tsinghua University：Sci ＆ Tech，1998，38（8）：114－117.

［2］孙伟，汪博，闻邦椿.高速主轴系统静止及运转状态下动力学特性对比分析［J］.机械工程学报，2012，48（11）：146－152.SUN Wei，WANG Bo，WEN Bangchun.Comparative analysis of dynamics characteristics for static and operation state of highspeed spindle system［J］.Journal of Mechanical Engineering，2012，48（11）：146－152.

［3］刘桂珍，刘杨，陈亚哲，等.转子－轴承系统油膜力特征的非线性动力学分析［J］.中国工程机械学报，2012，10（2）：127－131.LIU Guizhen，LIU Yang，CHEN Yazhe，et al.Nonlinear dynamical analysis on oil－membrane force properties for rotorbearing systems ［J］.Chinese Journal of Construction Machinery，2012，10（2）：127－131.

［4］LYRIDIS，DIMITRIOS V，PERAKIS，et al.Structural reliability analysis of marine diesel engine shafting systems：an equivalent stationary process approach to the level crossing problem［J］.Journal of Ship Research，1994，38（3）：253－258.

［5］LARMI M.Torsional vibration analysis of internal combustion engine shafting system－Preface ［J］.Acta Polytechnica－Scandinavica Mechanical Engineering Series，1996，119：2－7.

［6］朱朝宽，曾晓松.圆柱齿轮的装配误差对齿轮工作性能的影响分析［J］.机床与液压，2007，35（4）：5－8.ZHU Chaokuan，ZENG Xiaosong.The influence of assembling error on working performance of cylinder gear［J］.Machine Tool ＆ Hydraulics，2007，35（4）：5－8.

［7］李润方，龚剑霞.接触问题数值方法及其在机械设计中的应用［M］.重庆：重庆大学出版社，1991.LI Runfang，GONG Jianxia.Numerical method of contact problem and its application in mechanical design［M］.Chongqing：Chongqing University Press，1991.

［8］孙志星.考虑装配误差的齿轮接触应力仿真研究［D］.太原：太原理工大学，2010.SUN Zhixing.Contact stress simulation study of gears with assembly error ［D］.Taiyuan：Taiyuan University of Technology，2010.

［9］伍生.基于滚动轴承接触问题的有限元分析［D］.呼尔浩特：内蒙古工业大学，2007.WU Sheng.The finite element analysis basing on the contact problem for roll bearing ［D］.Hothot：Inner Mongolia University of Technology，2007.

［10］JOHNSON K L.Contact Mechanics ［M ］.Cambridge：Cambridge University Press，1985.