基于场路耦合法的大型异步电机气隙磁场研究

李爱平，宋守泰，刘雪梅

（同济大学 机械与能源工程学院，上海 201804）

在传统电机设计中，异步电机的参数主要是根据磁路法和经验公式进行计算.但是，由于电机复杂的边界形状、非线性（铁心饱和）及集肤效应等因素，磁路法计算无法得到准确的结果，而基于有限元方法的场分析对于电机电磁参数的计算就很有优势.而另一方面，电机的端部由于其联线方式的复杂性，用场分析的方法很难实现，只有采用路来代替，而路的参数可用经典电机设计程序计算，所以，利用场路耦合法分析电机电磁场，可以获得高精度的计算结果［1］.

异步电机气隙谐波磁场对电机设计、制造、运行极其重要，它影响了电机的感应电动势、转矩特性、附加损耗和振动噪声等，而对噪声尤为敏感［2］.异步电机运行时，电机的气隙谐波磁场包括时间谐波磁场和空间谐波磁场.其中，时间谐波磁场是由变频器中谐波电流引起的，而空间谐波磁场是由电机本身的结构特性引起的.异步电机气隙中的空间谐波磁场主要包括两部分：一部分是定子、转子绕组磁势在气隙中建立的谐波磁场；另一部分是定子、转子铁心开槽引起的气隙磁导齿谐波磁场［3］.

文献［4］用解析法研究了定子开槽对异步电机气隙磁场的影响.文献［5］和［6］研究了无刷双馈电机中不同绕组电流产生的谐波磁场以及两相异步电机中不同的绕组结构对气隙磁场谐波的影响.文献［7］和［8］分别利用有限元法对多相同步发电机气隙磁场和空载特性进行了分析计算以及对谐波励磁同步发电机空载谐波磁场进行了研究.本文利用有限元法计算大型异步电机的气隙磁场，不仅研究开槽对电机气隙磁场谐波成分的影响，同时通过对比电机空载时和额定运行时电机气隙磁场的谐波成分，定量研究电机磁场谐波成分及其与电机电磁参数的关系，为深入研究电磁噪声的机理及对电磁噪声的控制技术提供参考.

1 场路耦合法

图1为笼型感应电机的等效电路.图中R1为定子绕组的电阻；U1为外施相电压；I1为定子绕组相电流；E1为感应电动势；X1σ为定子漏抗，包括定子槽漏抗X1σ（S），谐波漏抗X1σ（D）（X1σ（S＋D）为定子槽漏抗和谐波漏抗之和）和定子端部漏抗X1σ（E）；Xm为激磁电抗，Rm为激磁电阻；R′2为转子电阻的归算值，包括导条电阻的归算值R′2（B）和端环电阻的归算值R′2（R）；X′2σ为转子漏抗的归算值，包括转子槽漏抗的归算值X′2σ（S）、谐波漏抗的归算值X′2σ（D）（X′2σ（S＋D）表示转子槽漏抗和谐波漏抗的归算值之和）和端环漏抗的归算值X′2σ（R）.由于有限元计算是作为二维问题在轴向有效长度内进行的，求解域仅包括定转子铁心、气隙和绕组的槽内部分，即图中虚线框内的部分，而没有包括定、转子绕组端部电阻和端部漏抗的影响，因此需要通过场路耦合的办法对有限元计算做出相应的修正.

图1 笼型感应电机的等效电路Fig.1 Equivalent circuit of squirrel－cage induction motor

1.1 定子路模型的建立

交流电压对电机定子绕组供电，定子三相绕组中会出现感应电势，定子绕组电动势是把定子场和路结合起来的关键参数.场路耦合法把电机的直线部分与端部分开考虑，如图2所示.在保证异步电机等效电路中阻抗不变即定子绕组电势不变的原则下，采用电路的方式来模拟电机端部的影响.对定子端部阻抗采用电阻和电感来等效其作用，同时为了计及谐波的影响，采用电感模拟定子谐波漏抗.图2中u为定子线圈相电压，i为定子线圈相电流，L1为定子线圈端部漏抗及谐波漏抗的等效电感，Ld为定子线圈直线部分的等效电感.

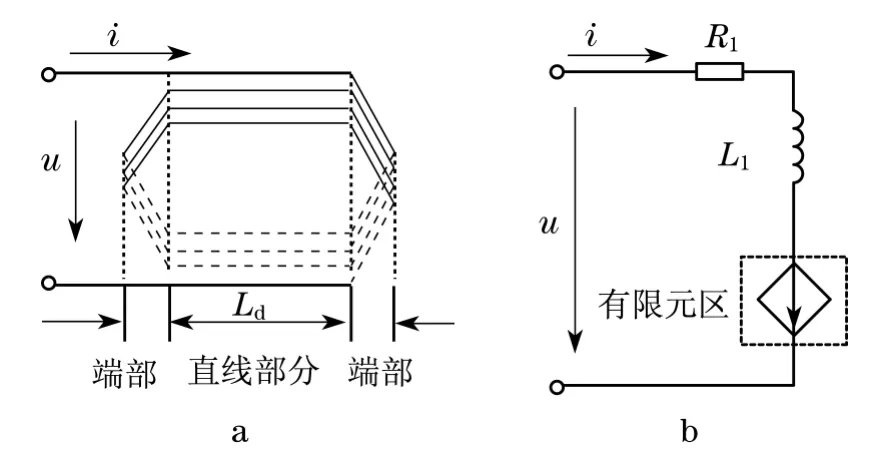
图2 定子场路耦合示意图Fig.2 Field－circuit coupled schematic of stator

定子线圈端部相电阻R1的计算公式为

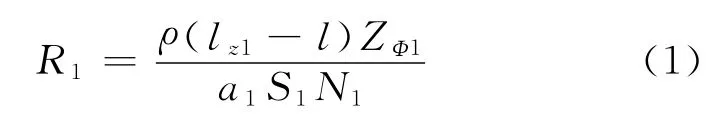
式中：ρ为导线电阻率；lz1为线圈半匝长；l为定子铁心长；ZΦ1为每相串连导体数；a1为定子绕组并联支路数；S1为每根导线截面积；N1为每支路导线并绕根数.

定子线圈端部漏抗及谐波漏抗等效电感的计算公式为

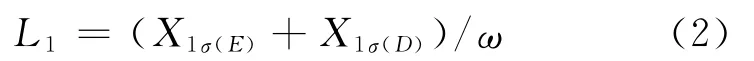
式中：ω为电机角速度.

1.2 转子端部电阻和漏抗的计及

定子绕组中感应电动势会随时间而旋转，而转子导条中也会因此感应出电动势，同时转子导体中会感应电流.转子场路耦合示意图如图3所示，采用电路的方式来模拟转子端部的影响.对转子端部阻抗采用折算导条电导率和磁导率的方法，将其计及到转子槽阻抗中.同时，为了计及谐波的影响，采用折算磁导率法将转子谐波漏抗折算到转子槽漏抗中.

图3中，k表示为第k根导条支路；R2（B）是每根导条的电阻；R2（R）是每段端环的电阻；Ik为第k根导条中的电流；为流经端环的电流；X2σ（B）和X2σ（R）分别为转子中每槽的槽漏抗和每段端环的漏抗.将转子端环电阻端环漏抗的影响计及二维电磁场计算，可把转子导条的电导率由σ2修改为，以把端环电阻并入导条内.考虑到导条的电阻与电导率成反比，故有

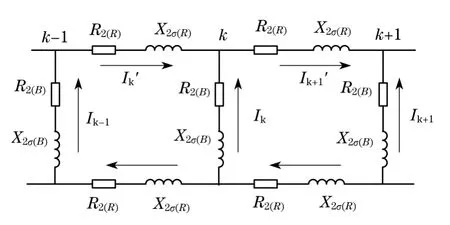
图3 转子场路耦合示意图Fig.3 Field－Circuit coupled Schematic of rotor

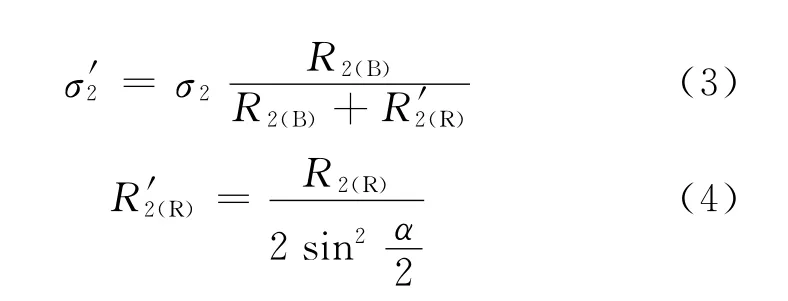
同理，为计及转子端环漏抗的影响，可把转子导条磁导率由μ2修改为，考虑到漏抗与磁导率成正比，故有：

2 仿真实例建模

本文以YKS1000－4TH大型异步电机为研究对象，基本参数如表1所示.建立二维场仿真模型，如图4所示.此图形为电机的二维径向截面图，在仿真计算中假定电机沿轴向处处相同，亦即磁场沿电机轴向处处相同.

本文模型定义了两种单元，PLANE53和CIRCUIT124，二维场区域定义为PLANE53，路模型单元定义为CIRCUIT124.模型网格经划分后如图5所示.假设电机的电磁场全部局限于电机内，电机外无磁场泄漏，故可设电机定子外圆边和转子内圆边的矢量磁位为0.

表1 YKS1000－4TH电机基本参数Tab.1 Basic parameter of YKS1000－4TH motor

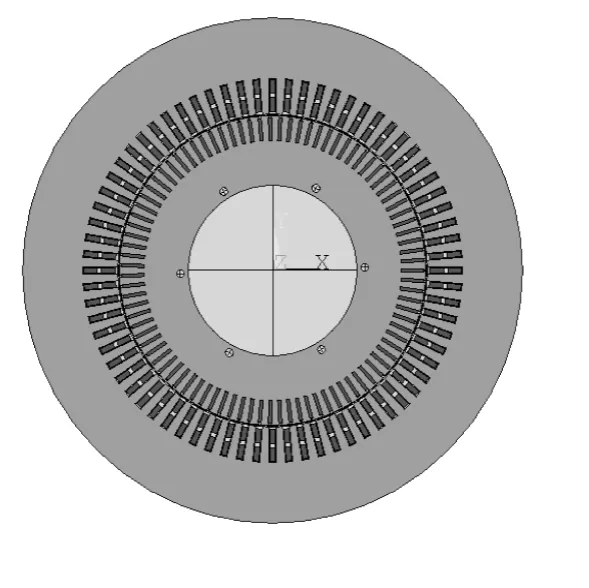
图4 电机的二维场模型Fig.4 2DField－model of motor

图5 电机的网格划分Fig.5 Map of mesh

YKS1000－4TH型电机定子绕组采用的是短距双层绕组，为三相四极电机，即m＝3，p＝2，定子槽数为72，线圈节距为y＝15，极距τ＝Z／2p＝18，每极每相槽数q＝Z／2pm＝6.电机转子槽数为91，导条在端部短接.

在二维场域模型的基础上，建立电机的电路模型，如图6所示.电路模型包括定子绕组端部电路、转子导条端部电路、电源和中性点.定子路模型采用一个电阻和一个电感串联作为两个槽之间的连接.对电路加载三相正弦电压源，电压源Y形连接.

图6 YKS1000－4TH异步电机路模型连接图Fig.6 Circuit－model Connection map of YKS1000－4TH asynchronous motor

3 仿真结果与分析

3.1 电机不同转速下的磁力线分布

图7a—d分别为电机在不同转速n下的磁力线分布图.在刚起动时，电机转速为零，磁力线穿过转子齿部形成闭合路径，转子导条集肤效应很明显，如图7a所示；随着电机转速上升，导体集肤效应减弱，磁力线开始向转子本体深层度渗透；当电机达到额定运行状态时，磁力线基本全部通过转子齿轭部分形成闭合回路，如图7c所示；在理想状态时，电机转速等于同步转速，磁力线穿过气隙全部通过转子齿轭部分形成闭合回路，如图7d所示.

3.2 电机不同负载下的运行情况

异步电动机空载运行时，电机转速n≈nN（nN为电机额定转速），转差率s≈0，磁力线穿过气隙全部通过转子齿轭部分形成闭合回路，此时输出功率为零，转子电流近似为零，定子电流近似等于励磁电流.随着负载增加，转速下降，转子电流增大，励磁电流基本不变，定子电流也增大，图8a，8b分别为电机空载运行和额定负载时电机电流密度分布图.

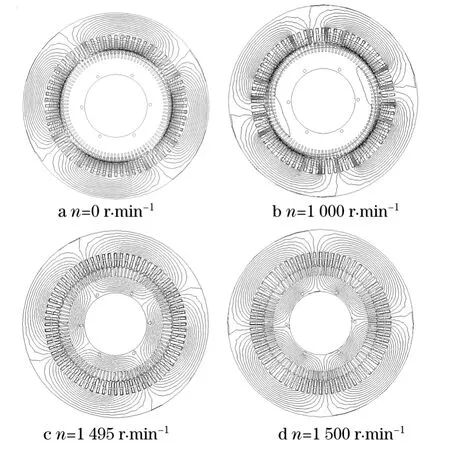
图7 磁力线分布图Fig.7 Distribution of magnetic flux line

图8 电机电流密度分布图Fig.8 Current density of motor

由图8可知，电机空载时转子电流近似为零，通过有限元计算可得出空载和额定负载时电机定子绕组电流值，如表2所示.通过与试验值进行对比可知，有限元法计算误差在允许范围之内，验证了有限元计算的准确性.

表2 有限元法与试验值比较Tab.2 Comparison of numerical stator current with FEM method with experimental values

3.3 电机空载气隙磁场分布

通过ANSYS分析可得到电机气隙磁通密度分布，将所得的数据导入MATLAB软件中可以得出电机不同状态下的气隙磁密分布，进行相应处理后可对异步电机气隙磁场特性进行分析.

图9为异步电机空载状态时一对极下气隙径向磁通密度的分布.由于漏磁场和谐波磁场的存在，气隙磁通密度呈现不完全的正弦分布.

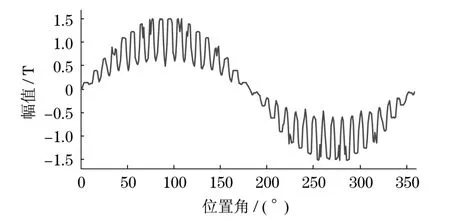
图9 电机空载时气隙磁场空间分布Fig.9 Air－gap flux densityof motor without load

气隙磁场波形中凹凸现象是由于电机开槽引起的气隙磁导变化导致的.对准齿部处的气隙较小，磁导大，而对准齿槽部处的气隙较大，磁导小，从而产生较强的齿谐波，气隙磁密在对准齿部处的值要大于对准槽部处的值.图10为电机定转子未开槽时的气隙磁场分布.在气隙空间内，气隙磁密呈现近似的正弦分布，但会出现小幅波动.此波动是由于电机定子绕组分散在槽里，绕组中绝缘以及绕组电流互相影响引起的.

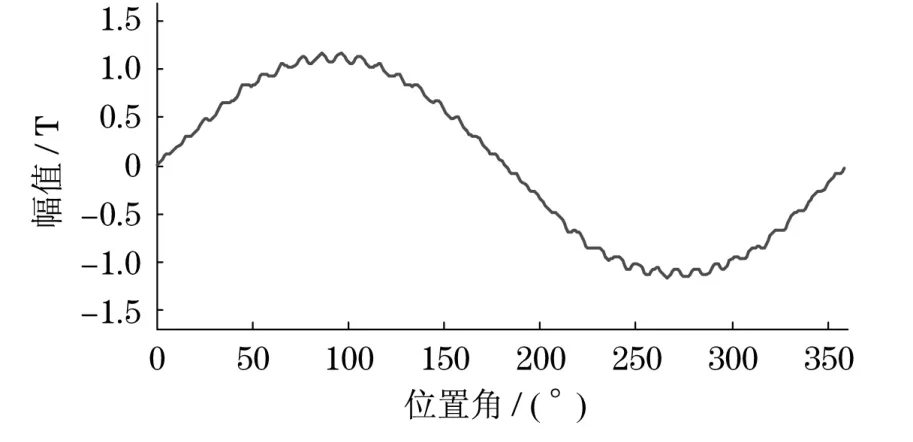
图10 定转子未开槽时的气隙磁场分布Fig.10 Air－gap flux density of motor without slotting in stator and rotor

整个气隙磁场波形可看作是由一个基波磁场和一个齿谐波附加磁场叠加而成，基波幅值达1.114T.齿谐波磁场分布如图11所示.可以被认为是一个以旋转的基波正弦曲线作为包络线的2mq（m为相数，q为每极每相槽数）次空间余弦谐波.

图11 齿谐波磁场Fig.11 Slot harmonic flux density

图12呈现了气隙磁密频谱分析结果，即对气隙磁密进行傅里叶分析，图中显示各高次谐波所占的百分值.可以看出，因齿槽的存在，加之气隙很小，气隙磁密分布很不均匀，其奇次谐波含量较大，尤其是35次和37次谐波，分别达到了22%和19%.

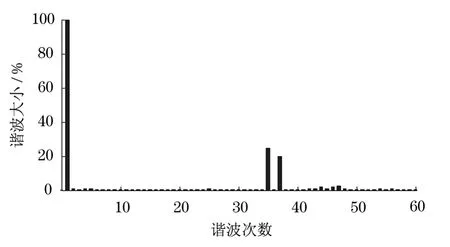
图12 电机空载时的气隙磁密空间分布频谱分析Fig.12 Spectral analysis of air－gap flux density of motor without load

通过对比图9和图10可知，定转子开槽对气隙磁场谐波有很大影响，故我们可以采取一定措施来削弱气隙谐波磁场，例如，减小槽口宽度，采用半开口槽或闭口槽，或者采用磁性槽楔.

3.4 电机额定负载气隙磁场分布

图13为异步电机在额定运行状态时一对极下气隙径向磁密的分布.由图可知，电机负载时明显地改变了电机的动力特性，对电机的模态特性产生了显著的影响，从而引起电机噪声的变化.

定子谐波磁通分量是由定子绕组谐波和齿谐波两部分的矢量合成决定的，它是电机产生振动及噪声的主要原因.比较图9和图13可知，异步电机在空载状态下定子齿谐波的幅度要比绕组谐波的幅度大得多，故空载时的噪声主要取决于齿谐波的大小.但定子齿谐波的幅度与负载的关系不大，而绕组谐波的幅度与定子电流成正比，电机在负载时的气隙磁密比空载时的气隙磁密大，且由于负载时转差频率的存在，电机在负载时的谐波频率与空载时有所不同，电机的振动和噪声要比空载时候大.

图13 电机定额负载时的气隙磁场空间分布Fig.13 Air－gap flux density of motor with rated load

图14为额定负载时气隙磁密频谱的分析结果.由图可看出，额定负载时电机气隙谐波次数含量较广，5次、7次、11次、13次、23次，25次，29次，31次，35次和37次谐波含量较大，分别为7.8%，3.7%，8.9%，6.3%，4.8%，4.0%，1.6%，2.7%，32.4%和22.9%.对比图12和图14可知，电机负载时气隙磁场分布比空载情况更加复杂，低次谐波含量变高，高次谐波作用也更加明显，电机的振动和噪声要比空载时候更明显.

图14 电机定额负载时的气隙磁场空间分布频谱分析Fig.14 Spectral analysis of air－gap flux density of motor with rated load

4 结论

本文通过基于场路耦合法的有限元法计算分析了大型异步电机的电磁性能，得到电机不同转速下的磁力线分布，并计算得出空载和额定运行状态下的电流值与试验值比较，验证了所采取的场路耦合法有限元计算的准确性.通过有限元法计算和分析了空载和额定负载下电机气隙磁通密度分布并对其进行比较，研究电机气隙磁场谐波成分与电机开槽和电机负载的关系，对于后期深入研究电磁噪声的机理及对电磁噪声的控制具有重要意义.

［1］周剑明，邵可然，周克定.异步电机场路耦合数值模拟方法［J］.大电机技术，1995（2）：28－33.ZHOU Jianming，SHAO Keran，ZHOU Keding.Field－circuit coupled numerical modelling method for indction motors［J］.Large Electric Machine and Hydraulic Turbine，1995（2）：28－33.

［2］白文俊.电机中的谐波磁场和噪声［J］.微电机，1985（2）：15－22.BAI Wenjun.Harmonic magnetic field and noise in asynchronous motor［J］.Micromotors，1985（2）：15－22.

［3］海勒尔B.异步电机中谐波磁场的作用［M］.北京：机械工业出版社，1980.HELLER B.Effect of harmonic magnetic field on asynchronous motor［M］.Beijing：China Machine Press，1980.

［4］李哲生.定子槽开口对异步电机气隙磁场和等效电路的影响［J］.大电机技术，1978（3）：71－78.LI Zhesheng.Influence of stator slot opening on air－gap field and equivalent circuit in asynchronous motor［J］.Large Electric Machine and Hydraulic Turbine，1978（3）：71－78.

［5］杨向宇，蔡晓铭.无刷双馈调速电机的谐波磁场分析［J］.华南理工大学学报：自然科学版，2005（4）：10－14.YANG Xiangyu，CAI Xiaoming.Harmonic magnetic field analysis of brushless doubly－fed machines for adjustable speed drives［J］.Journal of South China University of Technology：Natural Science，2005（4）：10－14.

［6］王胜博，张存山，孙起山.两相异步电机绕组结构对气隙磁场的影响［J］.电子器件及应用，2012，14（10）：42－46.WANG Shengbo，ZHANG Cunshan，SUN Qishan，et al.Influence of two winding structures on air－gap field in two－phase asynchronous motor［J］.Electronic Component ＆ Device Applications，2012，14（10）：42－46.

［7］ZHANG Y，SUN M，GUO P.No－load characteristics analysis and rated field current calculation of multi－phase synchronous generator based on nonlinear with FEM［J］.IEEE Electrical and Control Engineering，2011（9）：1628－1632.

［8］黄劭刚，夏永洪，张景明，等.谐波励磁同步发电机空载谐波磁场分析［J］.电机与控制学报，2005（1）：55－58.HUANG Shaogang，XIA Yonghong，ZHANG Jingming，et al.The analysis of no－load harmonic electromagnetic field of a harmonic excited synchronous generator［J］.Electric Machines and Control，2005（1）：55－58.

［9］戴文进，张景明，张莉，等.电机设计［M］.北京：清华大学出版社，2010.DAI Wenjin，ZHANG Jingming，ZHANG Li，et al.Design of electrical motor［M］.Beijing：Tsinghua University Press，2010.