得到中的“舍去”

王鸳

【摘 要】针对教师不深入解释问题的现象，本文以《梯形面积》为例，证明了教学活动的开展，应从学生的最近发展区出发；课堂教学的示范，更应注重学生的可持续发展；教学方法的优化，不等同于放弃其他方法的优势。

【关键词】梯形面积；最近发展区；教学方法优化

在“梯形的面积”的教学听课活动中，教师提问能把梯形转化成怎样的图形时，学生在完成了“用两个完全一样的梯形拼成一个平行四边形”后，竟一边倒地“沿梯形一边的高给剪下”，而后再无他法！与此同时，执教老师也并未对此行为作深入的分析与解答，课堂就这样陷入了沉寂。对此，笔者结合自身教学实践，谈谈自己的看法。

一、教学活动的开展，应从学生的最近发展区出发

【质疑】

当出现开头的这一幕时，不少执教老师都将它搁置在一边，不作过多的解释，这的确让人疑惑。

【分析】

就此情况，本人与几位执教老师进行了如下简短的交谈。

问：学生的这一“生成”（指学生“沿梯形一边的高给剪下”），是真实地反映了当前学生的学习情况吗？

答：应该是的。

问：那这一“生成”还能补救吗？

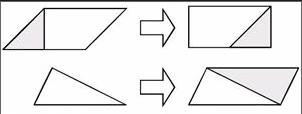
答：当然能（如图1所示）。

（图1）

问：那为什么不选择当场解答呢？

答：有过这样考虑。但基于以下三点只好作罢：首先，我必须得向学生解释为什么求梯形的面积时还得剪下另一边的高（而求平行四边形的面积时则不用）；其次，学生在理解剪、拼后得到的新三角形的底边边长，与原来梯形的上底和下底的底边边长之间的关系较为复杂；第三，如果对这一“生成”的处理花费过多的精力，那势必会影响当天的教学任务。

由此听来，本人不禁要发问：①“数学思维的培养是循序渐进的还是跳跃着前进的？那这样的做法还算得上是尊重学生的认知规律吗？”②“如果课堂总是选择脱离学生的“生成”，而改用一些比较好理解、好把握的方法来进行教学，那“优化”一词又该从何说起？”

【建议】

基于以上两点的考虑，笔者认为：首先，作为教师，我们要直面这些“生成”、巧用这些“生成”，最终趋利化弊、变废为宝。这是对学生学情的尊重，也是对课堂真实的尊重！其次，课堂一切教学活动的开展，都应该选择在学生相对熟悉的平台上来进行（而这个介于新旧知识之间的平台，称之为学生的最近发展区）。因此，教师在进行日常教学活动之前，一定要关注学生前后知识的衔接与过渡（即备教材），而教学活动的开展，则应该尽量选择从学生的最近发展区（即备学生）出发进行新知识的教授。

二、课堂教学的示范，更应注重学生的可持续发展

【问题】

学生为什么要沿梯形的一边的高剪下？

【分析】

究其原因，在回顾旧知环节，执教老师采用一边展示课件（如图2所示），一边让学生说明是怎样推导出平行四边形和三角形的面积公式的，意图是想让学生快速地回忆起“转化”这一重要的数学思想。而事实上，教师的良苦用心反倒造成了学生的思维定势，阻碍了学生思维的进一步发散，他们眼里看到的无一例外是两种“剪、拼”的转化方法，比如平行四边形在“转化”时所用的“剪、拼”方法就是将平行四边形的高剪下，然后再移动拼成长方形，这一成功的体验也驱使着他们对梯形也作如此的尝试。于是，他们竞相模仿课件的示范，便有了开头的这一幕。

（图2）

由此可见，学生对新知识的学习和接纳首先是靠模仿的，他们通过对课堂教学示范的模仿来达到对旧知识（或旧技能）的巩固和提升，从而使新知识得以理解并且掌握；而同时，学生的模仿也十分容易将原本热闹非凡的课堂推到冰点，使课堂教学陷入困局。因此，课堂教学中老师合理、正向的示范，就显得尤其重要。

【建议】

因此，在本人第二次教授《平行四边形的面积》时，就果断地采取了以下的示范（如图3所示）。

（图3）

在看到这样的示范后，老师们的批评如潮而至，简单总结起来就是：画蛇添足！其实不然。

第一，这样的示范是合理的，也更符合学生的认知规律。在学习《平行四边形的面积》之前，学生固有的知识就只有长方形（和正方形）的面积公式，故这节课主要向学生渗透“转化”这一重要数学思想和“剪、拼”这一重要转化方法。而当学生拿到平行四边形时，第一个感觉应该是要从平行四边形中找出长方形来，那所要做的必然是将平行四边形的两个高都给剪下（我想这才是学生的最近发展区）；在这之后，则是将余下的两直角三角形摆弄成另一个长方形。（而有些老师一开始就是采用“等底等高的长方形来覆盖”来达到找出平行四边形和长方形两者面积之间的关系，那试问：“等底等高”这样的示范又是建立在什么基础上呢？）

第二，这样的示范是正向的，因为它更关注学生的可持续发展。首先，这样的示范总共剪2次拼2次，自然不同于课本中的剪1次拼1次的示范，这样就为数学的优化（实质上是简化）铺平了道路；其次，这样的示范中出现的“将余下的两个直角三角形摆弄成一个长方形”，也悄悄地为下一节课《三角形的面积》的转化方法之一（用两个完全一样的三角形拼成一个平行四边形）埋下了伏笔；最后，这样的示范中出现的“剪左右两边的高”，更为现在研究的这一节课《梯形的面积》（再剪一次梯形的高）指明了方向。

鉴于此，建议教师们在日常教学中设计示范时，务必要着眼于学生可持续发展的最大化方向，最终让学生在课堂的模仿中能循着合理、正向的示范越来越务实，越来越创新，进而使模仿不再可怕，教学真正落至实处。

三、教学方法的优化，不等同于放弃其他方法的优势

【问题】

“学生为什么不尝试着沿另一边的高也给剪下来呢？”

【分析】

笔者想答案可能有二：其一，也许执教老师之前根本就没有给过学生这样的示范（如图3所示），学生没有这种体验，自然也就没有这样的尝试；其二，教师可能有过如图3的正向示范，但却被后来的课堂优化抹杀了。

优化可以方便记忆（比如我们只要知道两个完全一样的三角形可以拼成一个平行四边形，就可以马上自己推导出三角形的面积公式）；优化更容易导致忘记，特别是对于心智还不成熟的学生来说，很多时候他们对优化的理解就是记住最优解，忘记其他所有。

【建议】

可是，优化果真只是需要记住最优解吗？

显然不是。比如仅仅比较本文中的图2和图3，图2可以算得上是平行四边面积公式的推导方法的最优解了，可如果把它们一起搁置到梯形面积公式的推导方法中去，从考虑方法的可持续性发展出发，本人相信，大家都会更愿意选择图3的。

为了证明所说的，本人就以《多边形的面积》教学过程中的一连串正向示范和学生的有效模仿作为佐证。

（图4）

（图5）

与大家共享这些，除了想证明一堂课中的最优解不一定是一个章节中的最优解，还想证明在课堂中“优化”时被淘汰掉的差解也不一定都是最差解。而有时恰恰相反的是，看似繁琐、不易把握的方法，却极有可能是最符合学生认知规律、最适合学生可持续发展的方法，就比如上述的图4和图5，除了繁琐，它们甚至可以用“一招鲜，吃遍天”来形容，而且图中取高（或半高）、取中点（或中位线）的这些方式方法，将会在高年级的解析几何、立体几何的图形学习的添辅助线环节中发挥更强、更大的魅力。

因此，作为教师的我们更应该熟悉我们所教学科的教学体系，万不可为了眼前的蝇头小利，一叶障目，从而“舍去”了极有可能是从学生最近发展区出来的，也最有可持续发展势头的方式方法，最终给学生今后的学习生活蒙上了一层阴影。

参考文献：

[1]朱乐平.“平行四边形、三角形和梯形的面积公式教学研究”校本教研活动方案（二）[J].数学教学月刊（小学版），2011（12）.endprint