应力作用下石墨烯在磁场中的隧穿特性

马丽娜，张森，李荣华，阎维贤†

（1.山西大学 理论物理研究所，山西 太原 030006；2.山西大学 物理电子工程学院，山西 太原 030006）

0 引言

在紧束缚近似中［1］，能够得到石墨烯中的电子在K、K′点的行为类似于具有手征Dirac电子，但是运动速度却是光速的1／300［2－3］。这种特殊的性质使电子在石墨烯中具有量子电动力学中的相对论粒子的性质：例如Klein隧穿就是个例子，垂直入射的Dirac电子能够完全穿过任意高势垒。除此之外，Dirac电子也有着异常的物理性质，例如由于电子和空穴波函数的干涉引起的震颤，强磁场中的反常量子霍尔效应［4］，以及发生在单层石墨烯和超导材料薄膜的反常的Andreev反射［5］。正是由于单层石墨烯的电子具有Klein隧穿这样特殊的性质，使得把石墨烯中的电子控制在势垒中变得几乎不可能。但是近来的研究表明利用磁场反而可以有效地把Dirac电子控制在有效的范围内，从而为石墨烯电子学的应用提供了一个可能的选择［6］。一般情形下，大部分研究是集中在单层石墨烯中的电子或光学性质，但实际在应用上，石墨烯通常是生长在某种物理介质上，例如二氧化硅（SiO2）等绝缘基板上，由于晶格匹配的问题，往往产生应力，这些应力实际上会影响石墨烯中的最近邻的A，B子格子的隧穿，这种对最近邻隧穿的影响就表现在对理想单层石墨烯中的电子的哈密顿要进行必要的修正［7］。本文正是基于这种实际情形下的考量，对理想的单层石墨烯中的电子哈密顿做了各向异性的修正，研究石墨烯表面在磁场和应力共同作用下的电子的隧穿性质。我们利用转移矩阵的方法研究了电子在应力作用下矢势驱动的单层石墨烯单个势垒的透射性质，从而得到了透射率与入射粒子费米能以及势垒宽度的变化关系，并且讨论其与无应力情形下隧穿性质的比较，这些结果有利于深入揭示应力对石墨烯电子隧穿特性的影响。

1 应力下石墨烯模型

如果将上述修正的系统放在垂直于石墨烯表面（x，y）方向磁场下：即B＝B ez，在忽略电子自旋自由度的情形下，根据最小耦合原理，我们得到下列有效哈密顿量：

单层石墨烯实际上是由A，B两套子格子构成的一种二维六角形晶体，在紧束缚近似下：它的哈密顿量可以写成如下形式［2－3］：

其中电子动量为k＝－i（∂x，∂y）T，Pauli矩阵σ＝（σx，σy）作用在A，B 子晶格构成的赝自旋空间。石墨烯表面存在应力时，显示出各向异性，不失一般性，我们假定：有vx＝αvy，vy＝vF，α为应力相关因子，费米速度vF＝1.0×106m／s.

Fig.1 Schematic plot of the Dirac electrons in strained graphene driven by vector potential A（x）图1 Dirac电子在矢量势驱动的应变石墨烯的示意图

如果我们选择下列磁矢势A（x，y）＝A（x）ey（如图（1）所示），

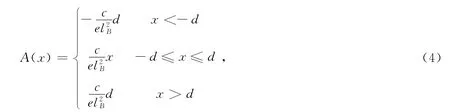
也就是说：图（1）中三个区域内，在｜x｜≤d处，B＝B ez，｜x｜＞d处，B＝0。

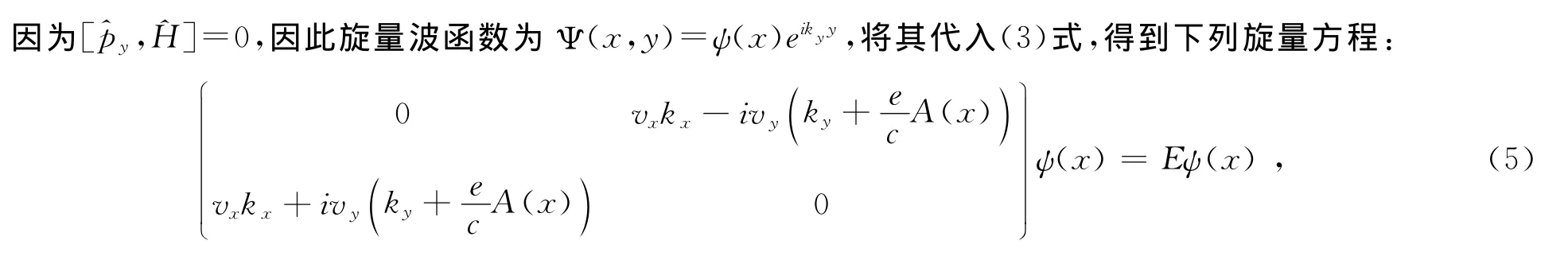
2 计算结果及讨论

图2描述应力和磁场共同作用下的石墨烯中Dirac电子在不同磁势垒宽度和以不同能量入射时，透射率随入射角度变化的规律。当B0＝4T时，lB＝13 nm，同时当εlB＝1时所对应的E＝44 me V。图2（a）与（b）描述了石墨烯在表面应力相关因子α＝0.75情形下，分别给出了（a）εlB＝5和（b）d／lB＝1.5，透射率随入射角φ变化的规律曲线。我们知道：如果系统所加的是电势，那么不论电势的势垒有多高，在电子垂直入射的情形下，电子的透射率都等于1，电子会完全穿过势垒，这也就是所谓的Klein隧穿［3］。但是，如果引入磁场，则会彻底改变这种状况，所以，磁场可作为约束Dirac电子处于某一范围内的有效手段。这种约束可以很清楚地在图2（a）和（b）看出来：图2（a）中d／lB＝3，4.5，4.97时，在垂直入射下透射率均为零。图2（b）εlB＝1.6时，透射率为零；εlB＝3.2时，尽管不为零，但明显小于1。

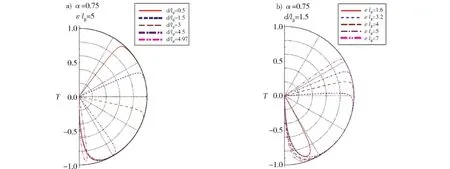
Fig.2 Two polar plots of the transmission under the same strain factorα＝0.75，（a）the same incident energy E＝220 meV，but different magnetic barrier width：d／l B＝0.5，1.5，3，4.5，4.97；（b）the same magnetic barrier width d／l B＝1.5，but with different incident energies：εl B＝1.6，3.2，4，5，7图2 透射率的极坐标图，应力相关因子α＝0.75，（a）入射能量等于220 me V情形下，磁势垒宽度2d不同时透射率的变化情况；（b）磁势垒宽度2d＝39 nm情形下，入射能量不同时的透射率

为了定量评估应力对于Dirac电子的输运性质的影响，我们在图3中给出了理想的单层石墨烯和应力作用下单层石墨烯的透射率随不同入射角度的变化情况。在图3（a）中，固定入射粒子的入射能量E＝70.4 meV和磁势垒宽度d＝19.5 nm。分别绘出了不同的应力相关因子下透射率随入射角的变化。在图3（b）中，画出了对应不同应力相关因子透射率的变化曲线，取较大的入射能量E＝220 me V，磁势垒宽度与图（a）相近：2d＝36.4 nm。因为两个子图的磁势垒宽度相近，入射电子能量有很大差距。图中可以看出，当入射能量较小时，粒子隧穿情况随应力的变化而有着明显的变化。随着能量变大，其变化越来越不明显，当能量较大如3（b）图所示，应力对透射率几乎没有影响。但是，对于入射能量较小的情形（如图3（a）所示），应力对透射率却有很大的影响。图3（a）中，实线给出了理想的单层石墨烯的透射率［6］，应力越大（α越小），透射率变化越大，当α＝0.7时，透射率可以达到1，在某个入射方向实现完全透射。

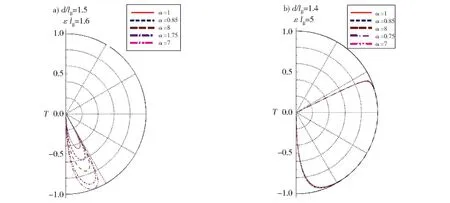
Fig.3 Polar plots of the transmission of Dirac electron under the strain.（a）small incident energy：d／l B＝1.5，εl B＝1.6；（b）large incident energy d／l B＝1.4，εl B＝5.0图3 石墨烯存在不同的应力情况下透射率的极坐标图，（a）能量较小下的情形d／l B＝1.5，εl B＝1.6；（b）能量较大的情形：d／l B＝1.4，εl B＝5.0

3 结论

本文主要研究了应变单层石墨烯穿过磁势垒的隧穿性质。通过引入应力相关因子研究了狄拉克电子在不同磁势垒宽度和以不同能量入射时，透射率随入射角度变化的规律，除此之外，还研究狄拉克电子在应力相关因子不同的情况下，磁势垒宽度和入射电子能量相同时，透射率随入射角度变化的规律。我们在整个空间区域构造了转移矩阵，通过连续性条件给出了穿过磁势垒的透射率的表达式。通过数值计算表明：在小角度散射中，磁场和应力对狄拉克粒子隧穿的影响与通常意义上的薛定谔粒子隧穿不同［9］，也与处于电势垒中的能完全透射的克莱因隧穿不同［3］，磁场和应力可以把狄拉克电子束缚在一个应变的磁势垒中。只要入射能量不是很大，应变的增加可以显著增加定向透射率，这种既能把狄拉克粒子约束在某个特定方向，而且又能通过应变调节透射率的大小在实际技术应用中很重要。同时我们发现在大的入射能量下，应变引起的效应会被消除，从而使得应变的石墨烯和理想石墨烯几乎具有相同的隧穿性质。

［1］ Wallace P.The Band Theory of Graphite［J］.Phys Rev，1947，71：622-634.

［2］ DiVincenzo D P，Mele E J.Self-consistent Effective-mass Theory for Intralayer Screening in Graphite Intercalation Compounds［J］.Phys Rev B，1984，29：1685-1694.

［3］ Neto A H C，Guinea F，Peres N M R，et al.The Electronic Properties of Graphene［J］.Rev Mod Phys，2009，81：109.

［4］ Gusynin V P，Sharapov S G.Unconventional Integer Quantum Hall Effect in Graphene［J］.Phys Rev Lett，2005，95：146801 1-4.

［5］ Beenakker C W J.Colloquium：Andreev Reflection and Klein Tunneling in Graphene［J］.Rev Mod Phys，2008，80：1337.

［6］ De Martino A，Dell’Anna L，Egger R.Magnetic Confinement of Massless Dirac Fermions in Graphene［J］.Phys Rev Lett，2007，98：066802.

［7］ Soodchomshom B.Valley-dependent Tunneling in a Monolayer Gapped Graphene Without Strain［J］.Physica E，2012，44：1617-1622.

［8］ Gradshteyn I S，Ryzhik I M.Table of Integrals，Series，and Product［M］.New York：Academic press，1965.

［9］ Ibrahim I S，Peeters F M.Two-dimensional Electrons in lateral Magnetic Superlattices［J］.Phys Rev B，1995，52：17321.