n维超立方体Qn中边不交的生成树

高太平，陈荷花

（1.山西大学 计算机与信息技术学院，山西 太原 030006；2.山西大学 计算智能与中文信息处理教育部重点实验室，山西 太原 030006；3.太原大学外语师范学院，山西 太原 030012）

0 引言

并行计算机互连网络是高性能计算机的研究重点之一。国内外现已对一些主要的并行计算机互连网络如Ring（环）、Tree（树）、Mesh（网格）、Torus（环绕）、Petersen（彼特森图）、Hypercube（超立方体）等进行了深入研究，并根据它们的拓扑结构研制出了相应的商用或研究用的并行计算机系统。由于超立方体互连网络的拓扑结构具有正则性、对称性、短直径性、可扩展性、可嵌入性、强容错性等性质，因此，一直深受研究者和应用开发者的偏爱，是最为重要和最具吸引力的并行计算机互连网络之一。近年来，不少学者已对它从不同方面进行了深入研究。

2007年，R.Cahalant等研究了超立方体中生成多路径问题［1］；2008年，P.Greger等研究了超立方体中路径分解问题［2］；2009年，X－B.Chen研究了超立方体中 many－to－many边不交路径问题［3］；2010年，Di liu等研究了n维超立方体中many－to－many路径覆盖问题［4］。2013年，Xie－Bin Chen和Shinhaeng Jo等分别研究了正常超立方体和带故障超立方体中配对many－to－many不相交路径全覆盖问题［5－6］。这些都是围绕超立方体互连网络中并行单播或组播路由问题所展开的理论研究，关于超立方体中并行广播路由的理论问题研究较少。

本文主要讨论超立方体互连网络Qn中边不交生成树数量的上界和下界，为进一步设计超立方体Qn中并行广播路由算法提供理论依据。因此，本文对并行计算机互连网络的研究与发展具有一定的理论意义和应用价值。

1 预备知识

图G是指一个有序的二元组（V（G），E（G）），其中V（G）是G的顶点集，V（G）中元素称为G的顶点或者节点；E（G）称为G的边集，E（G）中的元素称为G的边。设G是无向图，x∈V（G），EG（x）表示G中与x关联的边集；dG（x）＝｜EG（x）｜称为节点x的度；若图G中的每个节点的度都为k，则称图G为k正则的；在简单图中，可以用节点序列P＝（v1，v2，…，vn）来表示路P，或简记为P（v1，vn），其中v1和vn称为路P 的起点和终点，若v1＝vn，则称P为圈；包含G中的每个节点的路称为Hamilton路，包含G中的每个节点的圈称为Hamilton圈，包含Hamilton圈的图称为Hamilton图；设R为图G的一个子图，则称G－E（R）为R的补图，若V（R）＝V（G），则称R为图G 的生成子图；图G的连通分支数记为ω（G）；对图G1，G2，记G1＋G2＝（V（G1）∪V（G2），E（G1）∪（E（G2））。文中未定义的记号和术语，请参见文献［7］。

定义1 n维超立方体互连网络Qn是一个简单无向图，它由2n个节点和n·2n－1条边构成。每一个节点可由一个n位二进制串xn－1xn－2…x0进行编码，节点间的连接规则为：当且仅当其中两个节点的二进制串恰有一位不同时，两节点相连。

图1给出了一个4维超立方体互连网络Q4的拓扑结构，图中有24＝16个节点和4×24－1＝32条边，图中还标识出了节点的编码（分别从0000到1111）。

由定义1易知，n维超立方体Qn也可由两个n－1维超立方体连接而成，连接方法为：对u∈V（），v∈V（），uv∈E（Qn），当且仅当u＝0xn－2…x0，v＝1xn－2…x0。

下列图2是4维超立方体Q4的一种同构拓扑结构，它在证明过程中使用起来更为方便。

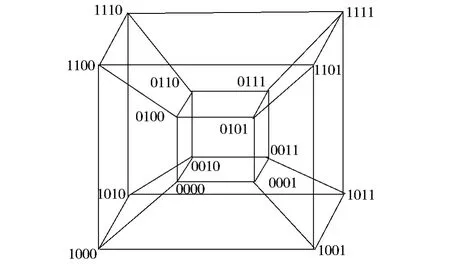
Fig.1 4－dimensional hypercube Q4图1 4维超立方体Q4

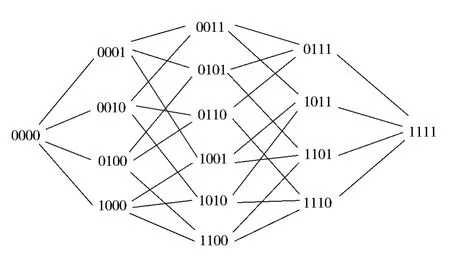
Fig.2 A topological structure of the hypercube Q4图2 超立方体Q4的一种同构拓扑结构

为了叙述方便，我们记Hn（vo，v）为超立方体Qn中起点为vo，终点为v的Hamilton路，当不关心终点时，也简记为 Hn（vo）。

定义2 若Qn中两棵生成树T1，T2具有相同的根节点，且E（T1）∩E（T2）＝φ，则称T1，T2为超立方体Qn中两棵边不交的生成树。记Γ（Qn）为超立方体Qn中以vo为根节点的全体边不交生成树的集合，或更具体地记为：

Γ（Qn，v0）＝｛Ti（v0）｜Ti（v0）为Qn中以v0为根节点的第i棵边不交生成树，i＝1，2…，k｝.为了证明我们的主要结果，还需下列引理：

引理1［8］当n≥2时，超立方体Qn是Hamilton图。

引理2［7］若ω（G）＝1，则图G中一定存在生成树。

2 主要结果

关于超立方体Qn中边不交生成树棵数的上界和下界，我们有下列两个结果。

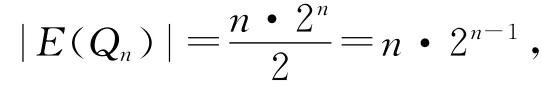
定理2 当n≥4时，超立方体Qn中至少存在2棵边不交的生成树，即

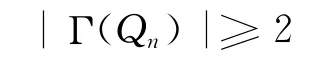
为了证明定理2，先给出以下两个断言：

断言1 超立方体Qn中存在以任意节点v0为起点的Hamilton路Hn（v0）。

证明 由引理1知，超立方体Qn中存在Hamilton圈，也就存在Hamilton路。在打开Hamilton圈时，可选择节点v0为起点的Hamilton路。从而得到Hamilton路Hn（v0）。

注1：该Hamilton路Hn（v0）即可作为Qn中的一棵以v0为根节点的生成树T1（v0）。

断言2 当n≥4时，超立方体Qn中Hamilton路Hn（v0）的补图是连通的，即：

证明 用数学归纳法。

（1）当n＝4时，Hamilton路H4（0000，0010）显然是超立方体Q4中的一棵以0000为根节点的生成树T1（v0）（见图3），而 H4（0000，0010）在Q4中的补图Q4－E（H4（v0））仍然连通（见图4），即ω（Q4－E（H4（v0））＝1。可见结论对n＝4成立。

Fig.3 A Hamilton path H4（0000，0010）in Q4图3 Q4中的一条 Hamilton路H4（0000，0010）

Fig.4 Complement of H4（0000，0010）in Q4图4 H4（0000，0010）在Q4 中的补图

（2）假设命题对n－1成立，即若Hn－1（v0）为n－1维超立方体Qn－1中一条以v0为起点的Hamilton路，则ω（Qn－1－E（Hn－1（v0）））＝1。

（3）下证命题对n成立。

设Hn－1（v0，v1）为超立方体Qn的n－1维子立方体中一条Hamilton路，Hn－1）为超立方体Qn的n－1维子立方体中与Hn－1（v0，v1）对应的Hamilton路，不妨记

为Qn中的一条Hamilton路（如图6中的虚线部分所示）。

下证Qn－E（Hn（v0））是连通的。

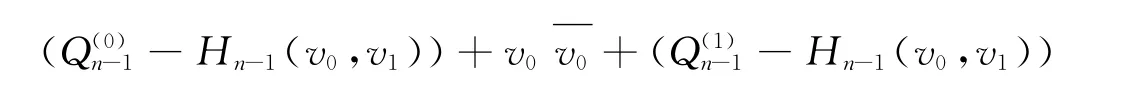
是连通的（如图6中实线部分所示），因此Qn－E（Hn（v0））也是连通的，即

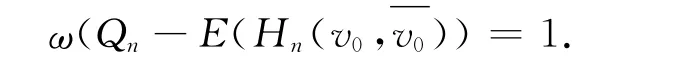
Fig.6 Illustration of the proving process for claim 2图6 断言2证明过程示意图

定理2的证明 由断言1可知，超立方体Qn中存在以任意节点v0为起点的Hamilton路Hn（v0），该Hamilton路Hn（v0）即可作为Qn中的一棵以v0为根节点的生成树T1（v0）；由断言2可知，ω（Qn－E（Hn（v0））＝1，即 H（v0）的补图 Qn－E（Hn（v0））是连通的，再由引理2知，Qn－E（Hn（v0））中存在生成树T2（v0）。由于 Hn（v0）与Qn－E（Hn（v0））互为补图，因此，T1（v0）和T2（v0）即为超立方体Qn中2棵边不交的生成树。

3 总结与展望

本文主要讨论了n维超立方体Qn中边不交生成树数量的上界和下界，证明了当n≥4时，n维超立方体Qn中边不交生成树数量介于2和之间。这就保证了n维超立方体Qn中至少存在2棵边不交生成树，因而在n维超立方体Qn中至少可进行双任务并行广播通信。由此可见，本文的研究结果为设计超立方体Qn中双任务并行广播路由算法提供了理论依据。如何设计快速有效的双任务并行广播路由算法，是我们进一步要研究的课题。

另外，不难看出，随着n的增大，n维超立方体Qn中边不交生成树的数量也会增多，从而｜Γ（Qn）｜的下界也会增大。｜Γ（Qn）｜与n的精确关系是什么，也有待进一步研究。因为只有知道了｜Γ（Qn）｜，才有可能设计出执行｜Γ（Qn）｜（大于2）项任务的并行广播路由算法。当然，设计相应的多任务并行广播路由算法等相关内容也有待进一步研究。

［1］Cahalant R，Koubek V.Spanning Mult－paths in Hypercubes［J］.Discrete Math，2007，307：2053－2066.

［2］Greger P，Dvorak T.Path Partitions of Hypercubes［J］.Information Processing Letters，2008，108：402－406.

［3］Chen X B.Many－to－many Disjoint Paths in Faulty Hypercubes［J］.Information Sciences，2009，179：3110－3115.

［4］Liu Di，Li Jing.Many－to－many Path－covers in n－dimensional Hypercubes［J］.Information Processing Letters，2010，110：580－584.

［5］Chen Xie－bin.Paired Many－to－many Disjoint Path Covers of Hypercubes［J］.Information Sciences，2013，179：3110－3115.

［6］Jo Shinhaeng，Park Jung－Heum，Chwa Kyung－yong.Paired Many－to－many Disjoint Path Covers in Faulty Hypercubes［J］.Theoretical Computer Science，2013，10：1－24.

［7］徐俊明.图论及其应用［M］.合肥：中国科学技术大学出版社，2004.

［8］Saad Y，Schultz M H.Topological Properties of Hypercubes［J］.IEEE Transactions on Computers，1998，37（7）：867－872.