粒子在非均匀环上的量子行走

梁树琴，李志坚

（山西大学 理论物理研究所，山西 太原 030006）

0 引言

量子行走是经典随机行走的量子力学推广［1－2］，它考虑了量子态的相干叠加特性。近些年，人们给出了基于量子行走的量子算法［3－4］，使得计算速度更快。与经典随机行走相比，量子行走具有更快的扩展速度、更短的混合时间［5］和命中时间［6］。随着研究的深入，研究者可以模拟许多实际生物、物理过程，如蛋白质折叠、光合作用［7］等等。

在经典随机行走的基础上，分离时间量子行走分别考虑了硬币空间和位置空间中的量子态的相干叠加效应，使得粒子在位置空间中发生弹道传输，是量子输运的有效模型。实验上可以用光纤、光格子、离子阱等物理系统模拟单个粒子的量子行走。目前人们热衷于多粒子的量子行走，增加了系统的自由度，使得更多的资源可以加以利用。离散时间量子行走中没有势能的作用，其相干特性完全由硬币态或作用于硬币态上的算符决定。文献［8］通过对比连续时间量子行走和分离时间量子行走的传输特性，得出可以通过改变硬币算符中的参数获得与改变量子势导致的相同效应，因此在分离时间量子行走中可以通过硬币算符的参数来等效量子势的作用，但文献［8］仅研究了单粒子在线上的散射效应，我们拓展到封闭环上两个粒子的散射效应，期望通过人为设置势垒来控制粒子的传播，研究等效量子势对量子行走的影响。

1 单粒子在环上的量子行走

离散时间量子行走在数学上与经典随机行走类似，首先执行一个硬币操作，然后根据硬币态决定粒子向哪个方向移动一步，如此不断循环。不同的是这里的硬币态不是仅处于头和尾两个态，而是可以处于它们任意的量子相干叠加态。系统的希尔伯特空间由硬币空间HC＝｛｜c〉：c＝1，2，…，d｝和位置空间HW＝｛｜x〉∶x＝1，2，…，N｝的直积构成。粒子每一步的演化算符U 由硬币算符C和条件平移算符S两部分组成，即

对于一维系统，每个格点有两个连接边，相应的硬币空间是一个二维空间，基矢记为｜↑〉和｜↓〉，则环上的条件平移算符S可表示为

也就是说当硬币态为｜↑〉时，粒子由格点x向右移动到格点x＋1；当硬币态为｜↓〉时，粒子由格点x向左移动到格点x－1。硬币算符C的选取并不是唯一的，为了简单，一般选择平衡无偏（向左、向右概率各为1／2）的Hadamard变换

本文我们研究由N个格点构成的封闭环上的量子行走，而且环上的格点是非均匀的，也就是说，环上的某些格点j和其他格点不同，在这些格点上的硬币操作算符不同于其他格点上的硬币操作算符，硬币操作算符是依赖于格点位置的，也就是

通常格点上使用硬币算符CH，而在这些特殊格点上使用硬币算符eiφCH。从散射角度说，这一相位因子的大小与势垒的大小在功能上相同，因此这些特殊格点被称为势垒［8］。考虑格点势垒后，演化算符（1）可表示为

其中｜ψ（0）〉为粒子的初始态，则粒子在格点上的概率分布为：

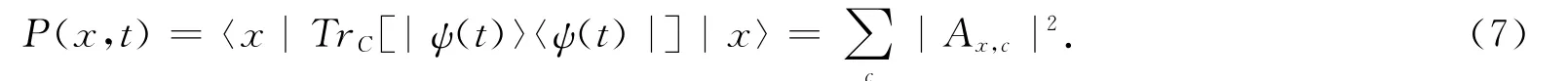
下面我们分别研究一个势垒和两个势垒对封闭环上单粒子量子行走的影响，势垒的大小取φ＝π，假定粒子初始时刻处于格点1的位置，且硬币态为（｜↑〉＋i｜↓〉），即

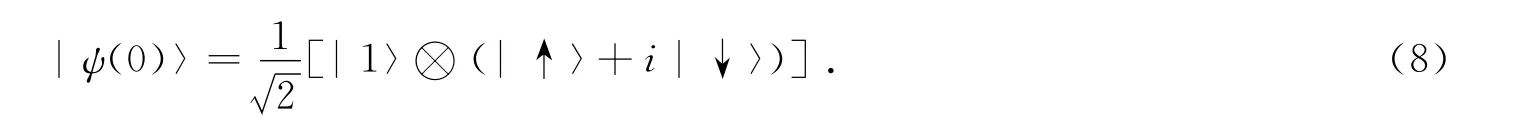
当环上的格点均匀，即没加势垒时，图1分别给出了格点数N为6、8时单个粒子在各格点上的分布概率随时间的变化曲线。从图中可以看出，当N＝8时，经过24步后，粒子回到了初始状态的概率分布，呈现出周期演化的动力学特性；而当N＝6时，不能表现出周期演化特性，呈无规的演化过程。而对于经典随机行走，无论格点数为多少，它都不会表现出周期演化的特性，只会像N＝6时的量子行走一样，经过无规律的演化步骤后可以回到初始时的分布状态。早在2003年，Tregenna等就曾经对均匀环上的量子行走进行过研究［9］，对于Hadamard硬币算符，当环上格点数分别为2、4、8时，演化过程具有周期特性，周期分别为2、8、24，但格点数为16时，却表现出无规的演化特性，即使经过成千上万步的演化，系统也不会回到初始时的分布状态。

Fig.1 Time evolution of the probability distribution for a walker on an uniform cycle，（a）N＝6；（b）N＝8图1 粒子在均匀环上各格点的概率分布随时间的变化：（a）N＝6；（b）N＝8

当环中只有一个格点与其他格点不同时，即在单势垒的情况下，图2分别给出了N为6、8时粒子在各格点上的分布概率随时间的变化曲线，当N为6时，势垒设置在格点x＝4处，当N为8时，势垒设置在格点x＝5处。从图2（b）可以看出，当N＝8时，均匀环时的周期演化特性被势垒破坏掉，呈现出无规的振荡变化。当粒子遇到势垒时，有一部分会被势垒挡住反射回去，有一部分会穿过势垒透射过去，透射和反射的多少由势垒的高度，也就是相角φ的大小决定。反射回去的粒子和下一步传输过来的相遇发生干涉，从而产生了更加复杂的干涉模式，破坏了原来的周期性。

当环中设置两个格点势垒时，图3分别给出N为6、8时，粒子在每个格点上的分布概率随时间的变化曲线，当N为6时，两个势垒分别设置在格点x＝3和x＝5处，从图3（a）中可以看出，在两个势垒间的格点x＝1，x＝2，x＝6上粒子的概率分布要比两个势垒另一侧的格点x＝4上的概率分布大。与图2（a）相比，此时势垒对粒子概率分布的影响更加明显，粒子在转移过程中，大部分被势垒挡住，发生了反射现象，只有小部分透射过去，粒子会在两个势垒之间来回反射，因此粒子在两个势垒另一侧的格点上的分布概率较小。当N为8时，两个势垒分别设置在格点x＝3和x＝7处，此时在两个势垒影响下粒子在各个格点上的分布概率表现出非常有趣的现象，如图3（b）所示，一方面由单势垒破坏掉的周期演化特性又重新出现，但与没有格点势垒的情况相比，其周期不再是24而是变为了48；另一方面与图3（a）相比，N＝8时粒子不再像N＝6时一样被束缚在两个势垒之间的格点x＝2，x＝8上，而是随着时间演化会有很大的概率透射到两个势垒的另一侧格点x＝4，x＝5，x＝6上，某些时刻粒子在格点x＝5处的分布概率可以接近1。整体来看，粒子的分布概率会在两个势垒格点的两侧随时间来回振荡。

Fig.3 Time evolution of the probability distribution for a walker on a cycle with two barriers，（a）N＝6；（b）N＝8图3 环上设置两个势垒时，粒子在非均匀环上各点的分布概率随时间的变化，（a）N＝6；（b）N＝8

2 封闭环上两粒子的量子行走

鉴于双势垒情况下，N＝8时单粒子演化分布概率表现出的周期特性，本节我们分析两个粒子在环上行走的联合概率分布。假定两粒子之间没有相互作用，侧重讨论两粒子硬币初态对概率分布的影响。每个粒子的时间演化算符Ui（i＝1，2）仍由方程（5）决定，则两粒子每一步总的演化算符可表示为

其中｜x1〉、｜x2〉、｜α1〉、｜β2〉分别表示两粒子的位置空间和硬币空间的基矢，｜ψ（0）〉12为两粒子的初始态，粒子在位置空间的约化密度矩阵为

在x1处找到粒子1，x2处找到粒子2的联合概率

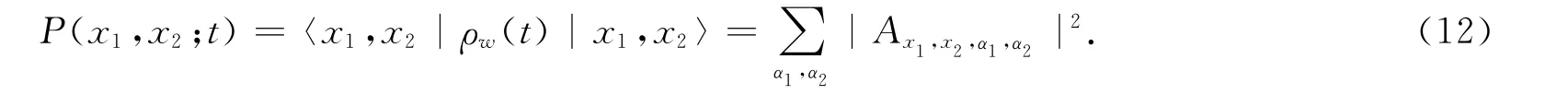
我们选取环的格点数N＝8，并在格点x＝3和x＝7处设置势垒，令方程（4）中的φ＝π。假定粒子1和粒子2的初始位置分别为x＝1和x＝5，两粒子的硬币初态选取两种情况，一种是非纠缠态｜↑〉1｜↑〉2，一种是纠缠态（｜↑〉｜↓〉＋｜↓〉｜↑〉），也就是两粒子的初态为1212

图4（1a－1d）、（2a－2d）分别给出在初态（13）、初态（14）下两粒子的联合概率在不同时刻的分布。x1，x2用来分别表示粒子1和粒子2所在的环上的格点位置，从图中看出，不论粒子的初始硬币态是纠缠态还是非纠缠态，当t＝4n（n为整数）时，两粒子的联合概率分布相同，特别是当t＝24时，两个粒子交换了格点位置，当t＝48时，两粒子再次交换位置回到初始时的联合概率分布状态。在其他时刻两种初态下两粒子的联合概率分布不再相同，当t＝11时，粒子只分布在偶数格点上，从图4（b）看出，初态（13）下粒子的联合概率分布达到了最大混合，所有偶数格点上的分布概率都相等，而初态（14）下两粒子在与势垒相邻格点上的联合概率为零，在其他偶数格点上出现的联合概率相等。特别值得一提的是在初态（13）下，当t＝10＋24n或t＝11＋24n（n为整数）时，两粒子的联合概率都会达到最大混合。

Fig.4 Joint position distribution of two walkers on a cycle with two barriers at certain time（a）t＝0，（b）t＝11，（c）t＝24，（d）t＝48.（1a－1d）and（2a－2d）are corresponding to the initial non－entangled state（13）and entangled state（14），respectively图4 N＝8时，两粒子在有两势垒的环上不同时刻（a）t＝0，（b）t＝11，（c）t＝24，（d）t＝48的联合概率分布图，（1a－1d）（2a－2d）分别表示非纠缠初态（13）和纠缠初态（14）下的演化

3 结论

本文由硬币算符中的参数来等效量子散射过程中的散射势，研究了封闭环上的势垒对分离时间量子行走的动力学演化的影响。分离时间量子行走的演化特征与环的格点个数有关，当格点数N＝8时，单粒子量子行走在均匀环上的概率分布随时间呈周期变化，单个势垒的散射能够破坏这种周期特性，双势垒散射却又使得这种周期变化特征重新恢复，而且周期扩大一倍，除此之外，粒子能透射势垒到达两个势垒的另一侧，表现出在两个势垒两侧来回振荡的特性。而当N＝6时，单个粒子的量子行走被束缚在两个势垒之间，粒子以较大的概率被势垒来回反射。最后，我们讨论了两个非相互作用的粒子在N＝8的环上受两个势垒散射的演化行为，以及这些行为与两个粒子初态之间的关系，发现在4的整数倍的时刻，两粒子量子行走在初态为纠缠态和非纠缠态两种情况下，两粒子的联合概率分布相同，如果初始时刻两粒子分别处于两势垒两侧的某一个点上，在半周期的时刻两粒子的位置互换。这些结果表明，无论是单粒子量子行走还是两粒子量子行走都可以作为一种有效的量子比特来进行量子计算。

［1］Aharonov Y，Davidovich L，Zagury N.Quantum Random Walks［J］.Phys Rev A，1993，48：1687－1690.

［2］Kempe J.Quantum Random Walk：an Introductory Overview ［J］.Contemporary Physics，2009，50（1）：339－359.

［3］Shenvi N，Kempe J，Whaley K B.Quantum Random－walk Search Algorithm ［J］.Phys Rev A，2003，67：052307.

［4］Hein B，Tanner G.Quantum Search Algorithms on a Regular Lattice［J］.Phys Rev A，2010，82：012326.

［5］Xu X P.Discrete－time Quantum Walk on One－dimensional Lattices［J］.Eur Phys J B，2010，77：479－488.

［6］Krovi H，Brun T A.Hitting Time for Quantum Walk on the Hypercube［J］.Phys Rev A，2006，73：032341.

［7］Mohseni M，Rebentrost P，Lloyd S，et al.Environment－assisted Quantum Walks in Photosynthetic Energy Transfer［J］.Chem Phys，2008，129：174106.

［8］Li Z J，Izaac J A，Wang J B.Position－defect－induced Reflection，Trapping，Transmission，and Resonance in Quantum Walks［J］.Phys Rev A，2013，87：012314.

［9］Tregenna B，Flanagan W，Maile R，et al.Controlling Discrete Quantum Walk：Coins and Initial States［J］.New J Phys，2003，83：1－19.