数形结合：数学解题方法归类叙论

尚会妍

天津商务职业学院，天津 300221

数形结合：数学解题方法归类叙论

尚会妍

天津商务职业学院，天津 300221

数形结合是解决数学问题的一种重要思想方法，在数学教学中占有重要地位。它是通过“以形助数，以数解形”的巧妙应用，使复杂问题简单化、抽象问题具体化，使问题能够轻松得到解决，从而起到事半功倍的效果。

数形结合；以形助数

数形结合是数学解题过程中采用的重要方法，从小学到大学、研究生考试、数学竞赛等都会涉及到数形结合的应用。运用数形结合的思想，不仅直观易发现解题途径，而且能避免复杂的计算与推理，大大简化了解题过程。在解选择题、填空题时更显其优越，注重培养这种思想意识，可以开拓学生的思维视野。本文就其应用的几种类型进行归纳总结。

一、利用韦恩图法解决集合之间的关系问题

例如：有48名学生，每人至少参加一个活动小组，参加数、理、化小组的人数分别为 28，25，15，同时参加数、理小组的有8人，同时参加数、化小组的有6人，同时参加理、化小组的有7人，问同时参加数理化小组的有多少人？

分析：用圆表示集合，用A、B、C分别表示参加数理化小组的人数，则三圆的公共部分则正好表示同时参加数理化小组的人数，用n表示集合元素的个数。

解：如图，

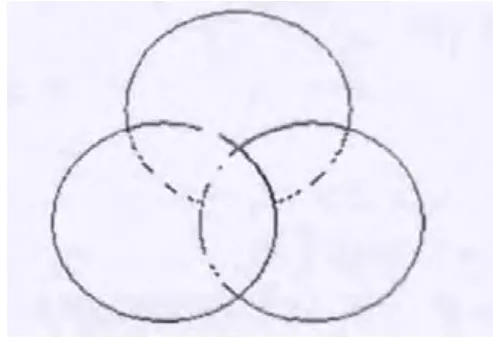
即 28＋25＋15－8－6－7＋n （A∩B∩C）=48， 则 n（A∩B∩C）=1，即同时参加数理化小组的有1人。

二、利用数轴解决集合的有关运算和关系问题

分析：若A∩B=φ，有如下图两种情况：

三、用一元二次函数的图像解决方程问题

例如：若关于x的方程x2+2kx+3k=0的两根都在-1和3之间，求k的取值范围。

分析：令f（x）=x2+2kx+3k，则f（x）的图像与x轴交点的横坐标就是方程f（x）=0的解。

解：由图可知，二次函数对称轴为x=-k，要使二根都在-1和3之间，

四、利用函数图像解决方程的近似解和解的个数问题

例1：解方程3x=2-x

分析：这是一个不规则的方程，直接解很困难，所以可以通过构造两个函数，然后把方程的根转化为两个函数的交点问题就好做多了。

解：由已知函数y=3x和函数y=2-x，通过图像可知两个函数的交点的横坐标即为方程的近似解。由图可知方程的近似解为x≈0.4。

例2：求方程lgx-sinx=0的解的个数。

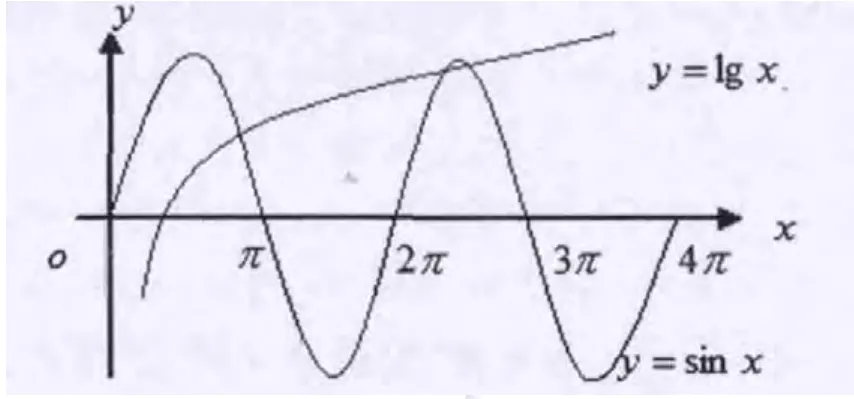
分析：此方程解的个数即为函数y=lgx与y=sinx的图像的交点个数。

解：因为 sinx≤1，所以 lgx≤1⇒0＜x≤10，由图可知两曲线有3个交点，故方程lgx-sinx=0有3个解。

五、利用几何图像解决函数问题

六、利用图像解决平面几何问题

例 2：如果实数满足等式（x-2）2+y2=3，那么的最大值是什么？

分析：将本题理解成直线和圆的位置关系，通过画图就能很直观地得出答案。

七、利用图像解决立体几何问题

例如：正方体ABCD-A1B1C1D1的棱长为a，求点B1到平面A1BC1的距离。

分析：通过图像利用体积相等即可。

解：设点B1到平面A1BC1的距离为h

当然，利用数形结合来解题的类型和方法还有很多，这里不再一一列举。通过研究使我们看到要在教学过程中逐步渗透数形结合的思想，让学生养成数形结合的良好习惯，使之成为分析问题和解决问题的工具。这样既能提高解题的效率，又能增强学生学习数学的兴趣。

［1］王君芬．例谈数学教学中的数形结合［J］．黑龙江科技信息，2009，（14）.

［2］蔡东兴．数形结合思想方法的应用［J］．高中数学教与学，2009，（2）.

［3］傅梦生．数形结合的应用策略研究［J］．科技咨询导报，2007，（11）.

［4］康小玲，等．数形结合法［J］.数学教学通讯，2002，（5）.

［5］袁小明．数学思想史导论［M］.南宁：广西教育出版社，1991.

Symbolic－graphic Combination： An Analysis on Classification of Mathematic Problem－Solving Methods

SHANG Hui－yan
（Tianjin College of Commerce， Tianjin 300221）

As an important method to solve mathematic problems， symbolic－graphic combination plays a very important role in mathematics teaching．By “combining numbers with shapes”， a complicated problem can be simplified and an abstract one embodied．As a result， some difficult mathematical problems can be solved in a simple way， getting twofold results with half the effort．

Symbolic－graphic Combination；combining numbers with shapes

O141.13

A

2095－5537（2014）01－00086－03

2013-12-26

尚会妍（1978—），女，汉族，天津市人，天津商务职业学院讲师。研究方向：应用数学。

责任编辑：周晓华 张 旭