数学例题教学之我见
2014-04-29王俊
王俊
【摘要】 例题的选取要紧扣本节课的知识目标,例题的选取要贴近学生的生活. 在例题教学中,要注意例题的引申和推广,在例题教学中,要充分调动学生的积极性,发挥学生的主体作用,挖掘课本例题,发挥课本例题的作用.
【关键词】 例题的重新加工;例题的引申;学生的主体作用;学生的思维;解题方法
例题是数学教材的重要组成部分,是教材的主要内容,是学生巩固基础知识、掌握解题思想方法的主要渠道,对培养学生良好的思维品质,对学生的能力培养起着非常重要的作用,是大面积提高数学教学质量的重要环节. 这就要求教师认真备课,充分发挥例题的作用. 下面我谈一下关于例题教学的五点见解.
一、例题的选取,要紧扣本节课的知识目标
数学课堂上一般是先进行知识点的教学,然后再进行例题的教学. 进行例题教学的目的是为了让学生掌握知识点的运用,因此,备课时要反复研究所设例题的内容是否紧扣本节课的知识点、数学思想及数学方法等. 例如人教版八年级数学上册“14.3.3一次函数与二元一次方程(组)”这一节,教材上设计了一道例3:
一家电信公司给顾客提供两种上网方式:方式A以每分0.1元的价格按上网时间计费;方式B除收月计费20元外再以每分0.05元的价格按上网时间计费. 上网时间为多少分,两种方式的计费相等?
就例3来看,列一元一次方程是完全能解答的问题,并且这种解法非常简单. 但教材安排例3的真正目的,是用函数方法来解. 因此,我在备课时对此例题进行了重新加工. 在已知条件不变的前提下,设计了以下五个问题:
(1)写出两种方式的收费y(元)与上网时间x(分)之间的函数关系式.
(2)在同一平面直角坐标系中画出函数的图像.
(3)求函数图像的交点坐标.
(4)上网时间为多少分时两种方式的计费相同?
(5)顾客应如何选择上网方式更经济?
这样重新设计后,它就是一道完整的函数题了,并且紧扣本节的知识目标和方法. 当然,不这样设计,硬用函数方法也能讲,但是学生是不会认可的,会认为没有必要.
二、例题的选取要贴近学生的生活
例题的选取要贴近学生的生活,是为学生所熟悉的内容,这样不仅可以激发学生的学习热情,还能发挥学生的创新意识和创造能力,从而增强学生学习数学的兴趣,有利于提高教学效果. 例3就是学生所熟悉的内容,贴近学生的生活,学生不仅用函数知识把问题解答了,而且进一步加深了对一次函数、一元一次方程、二元一次方程(组)、一元一次不等式的关系的认识.
三、在例题教学中,要注意例题的引申和推广
在例题教学中,要注意例题的推广和引申. 推广引申就是解完例题后,对原例题的条件、结论、题型作进一步的开拓思考,引申出新题和新的解法. 世界上的事物都是不断变化的,数学各知识之间也是相互依存、互相制约、不断变化的. 对例题进行推广引申,有利于把知识讲活,也有利于知识之间的内在联系,对培养学生的数学思维是大有益处的.
例如人教版八年级数学上册“14.3.3一次函数与二元一次方程(组)”这一节教材上的例3:一家电信公司给顾客提供两种上网方式:方式A以每分0.1元的价格按上网时间计费;方式B除收月计费20元外再以每分0.05元的价格按上网时间计费. 上网时间为多少分,两种方式的计费相等?
就本题而言,所求的问题是上网时间为多少分,两种方式的计费相等,可以把此问题进一步深化:顾客应如何选择上网方式更经济?
四、在例题教学中,要充分调动学生的积极性,发挥学生的主体作用
在例题教学中,要以学生为主体,给学生充分的活动时间,尽可能多地靠学生自己发现解题思路和动手作答. 可以通过小组合作、小组展示、学生点评来完成. 教师不要把例题的解法直接讲给学生,要充分相信学生,让学生在努力学习的过程中、在小组合作学习的过程中,实现学习目标,让学生获得成功的快乐. 学生亲自动手实践获取的知识,比老师讲授印象要深,记忆要牢固,更不容易遗忘. 有些老师经常说:这道题我都讲了四五遍了,学生还是不会. 我想,不妨你不讲,让学生亲自动手试试.
五、挖掘课本例题,发挥课本例题的作用
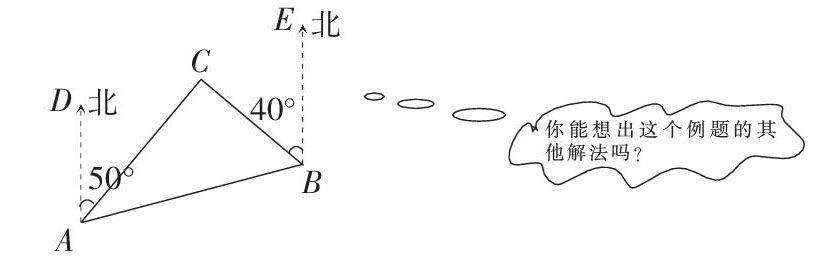
对课本上的例题,要认真挖掘,发挥好教材上例题的作用,尤其是一题多解和多题一解的例题更应给予高度重视. 因为通过一题多解、多题一解例题的教学,能够提高学生的思维能力、创新能力、分析问题和解决问题的能力, 能调动学生积极思维,提高学生的学习积极性. 例如人教版八年级数学上册第12页的例2:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向.从C岛看A,B两岛的视角∠ACB是多少度?
在课堂教学中,同学们通过小组合作学习,在课本解法的基础上又研究出了多种其他解法(例如:经过点C作CH∥BE;经过点C作MN∥AB;延长AC交BE于G等),有的小组还发现如果不给出“B岛在A岛的北偏东80°方向”这一条件,也可以求出∠ACB的度数. 通过这节课的学习,同学们不仅能够灵活运用三角形内角这一节课的知识解决问题,而且巩固了平行线的性质等知识,还探索出添辅助线的方法,同时,也提高了学生分析问题、解决问题的能力,丰富了学生们的解题方法. 你说,这道例题不是很好吗?
