整合相关教材资源，重组知识认知板块

陈兴国

[摘要]：现行初中数学课本中有不少例题内涵丰富，对发展学生思维能力有不同寻常的作用和丰富的教学价值，长期的教学实践使我体会到：如能对一些例题加以延伸和拓展，则能使学生以少胜多地巩固基础知识，提高分析问题和解决问题的能力，对沟通知识的联系、开拓思路、优化思维品质都是十分有益的。又逢我校开展“原生态教学”这一理念的探究，因此我们成立了针对教材中的例题进行拓展引申探究的小课题实验。

[关键词]：数学教学 例题 探究性学习

《数学课程标准》明确提出“人人学有价值的数学，人人都能获得必须的数学，不同的人在数学上得到不同的发展”。这就要求教师树立以学生发展为本的教育观，改革教学方法，激发学生学习兴趣，培养学生创新精神。教学内容必须面向每一个学生，体现教育的个性化，体现“低门槛，多层次”的基本思想。现行初中数学课本中有不少例题内涵丰富，对发展学生思维能力有不同寻常的作用和丰富的教学价值，长期的教学实践使我体会到：如能对一些例题加以延伸和拓展，则能使学生以少胜多地巩固基础知识，提高分析问题和解决问题的能力，对沟通知识的联系、开拓思路、优化思维品质都是十分有益的。又逢我校开展“原生态教学”这一理念的探究，因此我们成立了针对教材中的例题进行拓展引申探究的小课题实验。

一、例题的拓展引申，确保学生参与教学活动的持续的热情

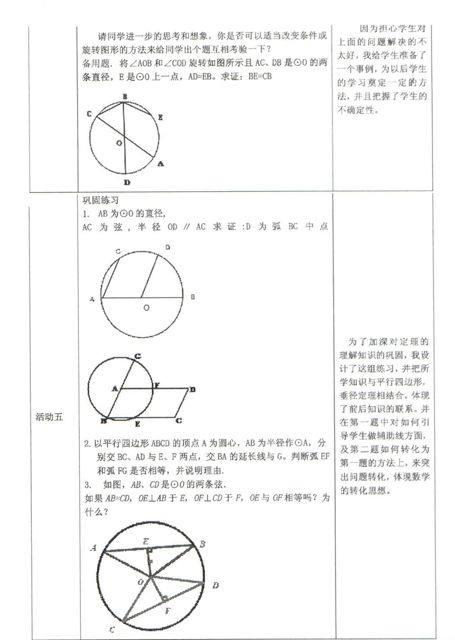
课堂教学效果很大程度上决定于学生的参与情况，这就首先要求学生有参与意识。加强学生在课堂教学中的参与意识，使学生真正成为课堂教学的主人，是现代数学教学的趋势。例题习题的变式拓展是对教学中的定理和命题进行不同角度、不同层次、不同情形、不同背景的变式，以暴露问题的本质，揭示不同知识点的内在联系的一种教学设计。通过例题习题的变式拓展，使一题多用，多题重组，常给人以新鲜感，能够唤起学生好奇心和求知欲，因而能够产生主动参与的动力，保持其参与教学活动的兴趣和热情。下面是我在浙教版九年级上册第三章第4节圆心角有关例题选择变式拓展教案的一部分。

这节课让学生都能进入到数学活动之中，但又不要求所有学生都达到相同的目标。学生参与教学活动的热情非常高，虽然设计的这节教学任务没有按计划完成，但超过了教学预想目标。学生下课之后还沉醉在课堂的讨论之中。

二、例题的拓展引申，培养学生思维的广阔性

思维的广阔性是发散思维的又一特征。思维的狭窄性表现在只知其一，不知其二，稍有变化，就不知所云。反复进行一题多变的训练，是帮助学生克服思维狭窄性的有效办法。可通过讨论，启迪学生的思维，开拓解题思路，在此基础上让学生通过多次训练，既增长了知识，又培养了思维能力。教师在教学过程中，不能只重视计算结果，要针对教学的重难点，精心设计有层次、有坡度，要求明确、题型多变的练习题。要让学生通过训练不断探索解题的捷径，使思维的广阔性得到不断发展。要通过多次的渐进式的拓展训练，使学生进入广阔思维的佳境。现在课本中，有一部分例题的“探究”“思考”是把例题进行变式训练的，我们可以利用它们切实培养学生思维的广阔性。

三、例题的拓展引申，培养学生思维的深刻性

例题变式拓展是指变换问题的条件和结论，变换问题的形式，而不变换问题的本质，使本质的东西更全面。使学生不迷恋于事物的表象，而能自觉地注意到从本质看问题，同时使学生学会比较全面地看问题，注意从事物之间的联系的矛盾上来理解事物的本质，在一定程度上可克服和减少思维中的绝对化而呈现的思维僵化及思维惰性。

例如，研究三角形的内角时设计的一个例题：如图在△ABC中，∠ABC，∠ACB的平分线交于点O，若∠A = 100°，求∠BOC的度数。

就设置以下问题：

①∠ABC，∠ACB的平分线交于点O可以得到哪些结论；

②∠2+∠4等于多少度？

③∠BOC与∠2，∠4的关系；

④当∠A=80°时，则图中的x是多少度？

⑤当∠A=y°时，则图中的x与y有何关系？

教师通过不断变换命题的条件，引深拓广，产生一个个既类似又有区别的问题，使学生产生浓厚的兴趣，在挑战中寻找乐趣，培养了思维的深刻性，同时也进一步巩固了对于三角形的内角和、角平分线的知识。

四、例题的拓展引申，培养思维的创造性

著名的数学教育家波利亚曾形象的指出：“好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在周围找一找，很可能附近就有好几个。”创新的成功直接依赖于努力钻研的坚韧程度。数学教学中由一个基本问题出发，运用类比、联想、特殊化和一般化的思维方法，探索问题的发展变化，使我们发现问题的本质。要注意主动地克服思维的心理定势，变中求进，进中求通，拓展学生的创新空间。教师结合典型例题，着意设计阶梯式的问题，引导学生的思维纵深拓展。如讲完例题（浙教版七年级上5.2解一元一次方程（一）课后练习2）：把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则缺23本，这个班有多少学生？

通过前面一些知识变式的铺垫，此题改编为：拓展（1）：把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分k本（k是小于10的正整数），则缺23本，这个班有多少学生？

拓展（2）：一队旅客乘坐汽车，要求每辆汽车的乘客人数相等，起初，每辆汽车乘了22人，结果剩下一人未上车；如果有一辆汽车空车开走，那么所有旅客正好能平均分乘到其它各车上，已知每辆汽车最多只能容纳32人，求起初有多少辆汽车？有多少名旅客？

数学课堂教学要把学生自主学习和主体智力参与，以及多向性、多层次的交互作用引进教学过程，才能使教学结构发生质的变化，才能使学生成为创造的主人。开展例题习题的拓展变式练习，有利于学生对实际问题的动态处理，克服思维和心理定势，实现创新目标。

在实验阶段，课题组成员除了遵循上述原则收集整理例题之外。还设计一些调查表对学生进行问卷调查，收集第一手反馈资料，进行反思整改。并且课题组成员都要写课后反思，并对主要问题大家探讨后进行重新整理。设计的调查问卷如下：

数学课堂教学及学生的学习状况问卷调查表

亲爱的同学，你好。我们进行了将近二个月新的教学模式的教学，为了了解你接受这种教学模式及学习数学的情况，我们设计了这份调查问卷。希望你认真填写，选择最适合你情况的序号，表达自己的真实感受和想法。这份问卷不记名，不计分，感谢你的真诚合作。

1.在数学课堂上，你对老师讲的内容感兴趣吗？（）

①非常感兴趣；②比较感兴趣；③一般；④不感兴趣；⑤非常讨厌

2.你喜欢怎样的学习方式？（）

①老师讲，我听；②按自己喜欢的方式学习；③与同伴合作、自主探究

3.你愿意对未知的数学问题开展探究吗？①愿意；②一般；③不愿意

4.课堂上你进行过探究活动吗？（）①经常；②偶尔；③从来没有

5.当你学习上遇到困难时，一般采用的方式是：（）

①向老师请教；②回去问家长；③求助于同学；④等待老师讲解；⑤和同学一起探讨

6.没有老师、家长的督促，你能好好学习吗？（）

①能；②不一定；③不能

7.讲新课前，你能自己进行预习，课后，能坚持认真复习吗？（）

①能坚持；②有时能；③不能

8.你对现在的教学模式感兴趣吗？为什么通过例题的拓展延伸你最大的收获是什么？你还有那些建议？你认为这种教学方法是否继续进行下去？

通过一年对数学课堂中例题的探究，对教师本身来讲提高了自身的素质，培养和锻炼了教师的教学反思能力，我们课题小组的成员在本市数学说课比赛中均获得不同层次的奖项，书写的教案均收集到学校的优秀教案之中。受益最大的莫过于学生，在本届中考数学中平均分都超市平均分很多。虽然一年的课题研究即将结题，但我们对例题教学的探究才拉开序幕。