Adaptive Iterative Learning Control for a Class of Nonlinear Time-varying Systems with Unknown Delays and Input Dead-zone

Jianming Wei Yunan Hu Meimei Sun

I.INTRODUCTION

F OR repeatable control tasks,iterative learning control(ILC)is themost suitable and effective control scheme.Now ILC can be classified into two categories,i.e.,traditional ILC[1−6]and adaptive ILC(AILC)[7−15].The control inputof traditional ILC is improved directly by a learning mechanism using the error and input information in the previous iteration.However,traditional ILC requires the global Lipschitz continuouscondition,whichmakes itdifficult to beapplied to certain systems.AILC is an alternative method to overcome this problem,which takes advantage of both adaptive control and ILC.In AILC,the control parametersare tuned in the learning process,and the so-called compositeenergy function(CEF)[10]is usually constructed to analyze the stability conclusions.In the pastdecade,several AILC schemes for uncertain nonlinear systems have been developed[11−15].

In practice,systems w ith time delays are frequently encountered.The existence of time delaysmay make the task more complicated and challenging,especially when the delays are not completely known.Stabilization problem of control systems w ith time delays has drawn much attention[16−18].A lthough many approaches have been developed in the field of AILC,only few results are available for nonlinear systems w ith time delay[19−21].An AILC strategy is developed for a class of simple fi rst-order system w ith unknown time-varying parameters and unknown time-varying delays in[20].In[21],an adaptive learning control scheme is designed for a class of fi rst-order nonlinearly parameterized systems w ith unknown periodically time-varying delays,and then is extended to a class of high-order systems w ith both time-varying and time-invariant parameters.However,they all require that the investigated uncertainties satisfy the local Lipschitz condition and nonlinearly parameterized condition such that adaptive learning laws can be designed to estimate the unknown timevarying parametersand the delay-independent terms produced by the derivative of Lyapunov-Krasovskii function can be compensated for directly by the controller.As much as we know,by now,no results have been reported for nonlinear systems that are not in parametric form and local Lipschitz.

Non-smooth and nonlinear characteristics such as deadzone,hysteresis,saturation and backlash,are common in actuatorsand sensors.Dead-zone isoneof themost importantnonsmooth nonlinear characteristics in many industrial motion control systems.The existence of dead-zone can severely impact system performances.It gives rise to design difficulty of controller.Therefore,theeffectof dead-zonehasbeen taken into consideration and drawn much attention in the control community for a long time[22−27].To overcome the problem of unknown dead-zone in control system design,an immediate method was to construct an adaptive dead-zone inverse.This approachwaspioneered by Tao and Kokotovic[22].Continuous and discrete adaptive dead-zone inverseswere built for linear systems w ith unmeasurable dead-zone outputs[23−24].Based on theassumption of the same dead-zone slopes in the positive and negative regions,a robust adaptive control method was presented for a class of special nonlinear systems w ithout using the dead-zone inverse[25].In the work of Zhang and Ge[26−27],the dead-zone was reconstructed into the form of a linear system w ith a static time-varying gain and bounded disturbances by introducing characteristic function.In[28],input dead-zone was taken into account and it was proved that the simplest ILC scheme retained its ability of achieving satisfactory performance in tracking control.As far as we know,there are few works from the viewpointof AILCwhich deals w ith nonlinear systems w ith dead-zone nonlinearity in the literature at present.

In this paper,we presenta neuralnetwork(NN)based AILC scheme for a class of nonlinear time-varying systems w ith unknown time-varying delays and unknown input dead-zone.Themain design difficulty comes from how to dealw ith deadzone nonlinearity and delay-dependent uncertainty that isneither parameterized nor local Lipschitz.In our work,the dead-zone output is represented as a novel simple nonlinear system w ith a time-varying gain,which ismore general than the linear form in[22].The approach removes the assumption of linear function outside the dead-band w ithout necessarily constructing a dead-zone inverse.An appropriate Lyapunov-Krasovskii functional and Young′s inequality are combined to elim inate the unknown time-varying delays,whichmakes NN parameterizations w ith known inputs possible.Radial basis function neuralnetworks(RBFNNs)areused asapproximator to compensate for the nonlinearunknown system uncertainties.Since the optimal weights for NNs are usually unavailable,adaptive algorithms are designed to search for suitable parameter values during the iteration process.Furthermore,the possible singularity which may be caused by the appearance of the reciprocal of tracking error,is avoided by employing the hyperbolic tangent function.By constructing a Lyapunovlike CEF,the stability conclusion is obtained in two cases by exploiting the propertiesof the hyperbolic tangent function via a rigorous analysis.In addition,the boundary layer function is introduced to remove the requirement of identical initial condition which is required by themajority of ILC schemes.

The restof this paper is organized as follows.The problem formulation and preliminaries are given in Section II.The AILC design is developed in Section III.The CEF-based stability analysis is presented in Section IV.A simulation example is presented to verify the validity of the proposed scheme in Section V,followed by the conclusions in Section VI.

II.PROBLEM FORMULATION AND PRELIM INARIES

A.Problem Formulation

In this paper,we consider a class of nonlinear time-varying systems w ith unknown time-varying delays and dead-zone running over a finite time interval[0,T]repeatedly,given by

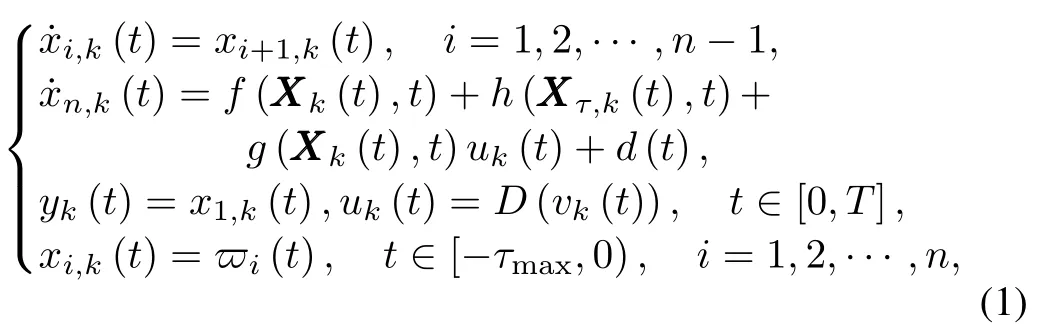
wheretis time,k∈N denotes the number of iterations,yk(t)∈R andxi,k(t)∈R(i=1,2,···,n)are the system output and states,respectively,X k(t):=[x1,k(t),x2,k(t),···,xn,k(t)]Tis the state vector,τi(t)are unknown time-varying delays of states andxτi,k:=xi,k(t− τi(t))(i=2,3,···,n),Xτ,k(t)=[xτ1,k(t),xτ2,k(t),···,xτn,k(t)]T,f(·,·)andg(·,·)are unknown smooth functions,h(·,·)is an unknown smooth function of time-delay states w ith upper bound,d(t)is unknown bounded external disturbance,ϖi(t)(i=1,2,···,n)denote the initial functions fordelayed states,vk(t)∈R is the control input,and the actuator nonlinearityD(vk(t))is a dead-zone characteristic which is described by

wherebr≥0 andbl≤0 are unknown constants,m(t)＞0 is unknown time-varying slope,vk(t)is the input anduk(t)is the output.A graphical representation of the dead-zone investigated in this paper is shown in Fig.1.

Fig.1. Dead-zonemodel.

The dead-zone outputuk(t)is not available formeasurement.The assumption on the dead-zone parameters is as follows.

Assumption 1.The dead-zone parametersbr,blandm(t)are bounded,i.e.,there existunknown constantsbrmin,brmax,blmin,blmax,mmin,mmax,such thatbrmin≤br≤brmax,blmin≤bl≤blmaxandmmin≤m(t)≤mmax.

From a practical point of view,we can re-define the deadzone nonlinearity as

w ith

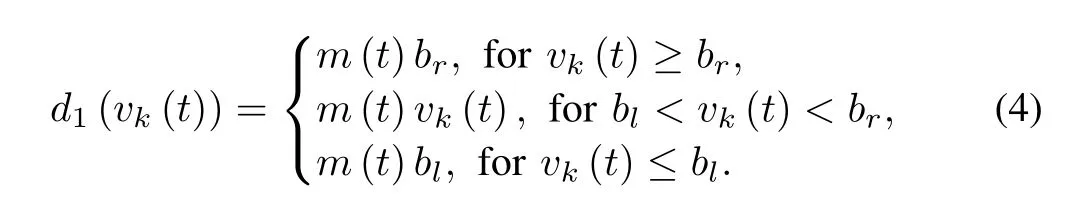
It is obvious thatd1(vk(t))is bounded.

In this paper,a desired trajectory for the state vectorX k(t)to follow is given byX d(t)=Define the state tracking errors aseeek(t)=[e1,k,e2,k,···,en,k]T=X k(t)−X d(t).The control objective of this paper is as follows.For the desired trajectoryX d(t),design an AILCuk(t),such that,all the signals remain bounded and the tracking errorek(t)converges to a small neighborhood of the origin ask→ ∞,i.e.,limk→∞‖eeek(σ)‖2dσ ≤ εesk,whereεeskis a small positive error tolerance and‖·‖denotes the Euclidian norm.Define the fi ltered tracking error asesk(t)=eeek(t),whereΛ=[λ1,λ2,···,λn−1]Tandλ1,λ2,···,λn−1are the coefficients of Hurw itz polynom ialH(s)=sn−1+λn−1sn−2+···+λ1.It is obvious that ifesk(t)approacheszero ask→ ∞,then‖eeek(t)‖w ill converge to the origin asymptotically.

To facilitate controlsystem design,the follow ing reasonable assumptions aremade.

Assumption 2.The unknown state time-varying delaysτi(t)satisfy 0≤ τi(t)≤ τmax,i(t)≤ κ ＜1,i=1,2,···,n,w ith the unknown positive scalarsτmaxandκ.

Assum ption 3.The unknown smooth functionh(·,·)satisfies

whereθ(t)is unknown time-varying parameter andρj(·)are known positive smooth functions.

Assumption 4.The sign ofg(·,·)is known,and there exist constants 0＜gmin≤gmaxsuch thatgmin≤|g(·,·)|≤gmax.Without loss of generality,we always assumeg(·,·)＞0.

Assum ption 5[14].The initial state errorsei,k(0)at each iteration are not necessarily zero,small or fixed,but assumed to be bounded.

Assum ption 6.The desired state trajectoryX d(t)is continuous,bounded and available.

Assumption 7.The unknown external disturbanced(t)is bounded,i.e.,thereexistsan unknown constantdmaxsatisfying|d(t)|≤dmax.

Remark 1.Assumption 2 is necessary for the control problem of time-varying delay systems,which ensures that the time-delay parts can be eliminated by Lyapunov-Krasovskii functional.And Assumption 2 ismilder than that in[19−21]which requires to know the true value ofτmaxandκ.

Remark 2.Assumption 3 ismild onh(·,·).Sinceh(·,·)is continuous on[0,T],h(·,·)is bounded,obviously.Compared w ith the assumption of local Lipschitz condition w ith known upper bound functions in[20−21],this assumption is largely relaxed and can be easily satisfied.Actually,ρj(·)are not necessarily known,they are approximated by NNs as part of the uncertainties,which w ill be given later.

Remark 3.The control gain boundsgminandgmaxare only required for analytical purposes,their true values are not necessarily known since they are not used for controller design.

B.A Motivating Example

In order to illustrate the main idea of CEF-based AILC,we fi rstly give a simple scalar system running over the time interval[0,T]w ith the follow ing dynam icmodel

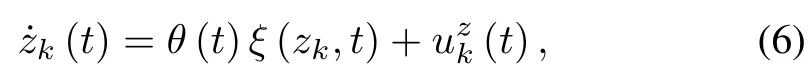
wherezk(t)is the system state in thek-th iteration,(t)is the control input,θ(t)isan unknown time-varying parameter,andξ(zk,t)is a known time-varying function.The desired trajectory forzk(t)iszr(t),t∈[0,T].Define the tracking error asezk(t)=zk(t)−zr(t)and design the control law for thek-th iteration as

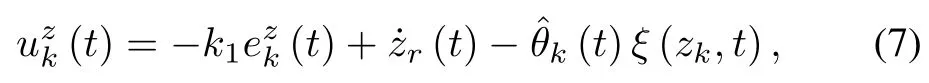
wherek1＞0 isa design parameterandk(t)is the estimation ofθ(t)in thek-th iteration.Design the adaptive learning law for the unknown time-varying parameter as(

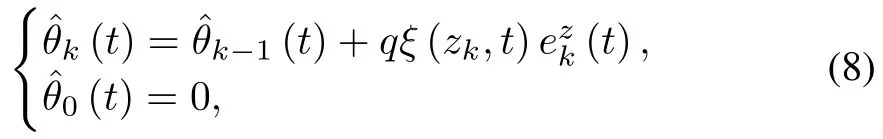
fort∈[0,T],whereq＞0 is the learning gain.

Define the estimate error as(t)=k(t)− θ(t).Then choose a Lyapunov-like CEF as follows:

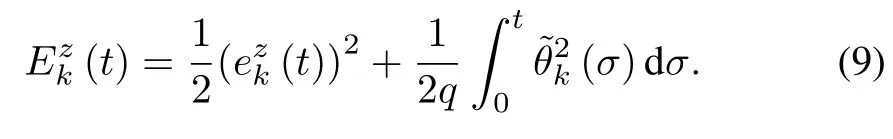
Throughout this paper,σdenotes the integral variable.Then it can be derived that

We can further obtain

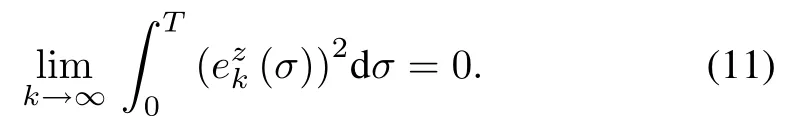
Thus,the system statezk(t)converges to the desired trajectoryzr(t)on[0,T]ask→∞.

III.A ILC DESIGN

Now,we use the follow ing process to explain the design approach.According to Assumption 5,there exist known constantsεi,such that,|ei,k(0)|≤ εi(i=1,2,···,n)for anyk∈N.In order to overcome the uncertainty from initial state errors,we introduce the boundary layer function[14−16]and define error function as follows:

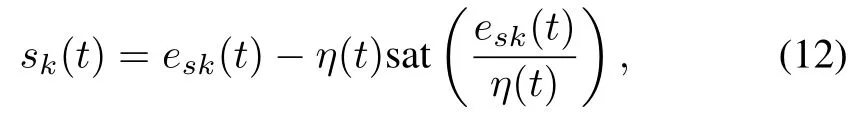
whereε=£ΛT1⁄[ε1,ε2,···,εn]T,Kis a design parameter,and saturation function sat(·)is defined as

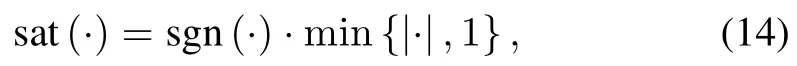
Remark 4.η(t)is time-varying boundary layer function.In[14],ithasbeen pointed out thatη(t)decreasesalong timeaxis w ith initial conditionη(0)=εand 0＜ η(T)≤ η(t)≤ ε,∀t∈[0,T],and ifsk(t)can be driven to zero∀t∈[0,T],then the states w ill asymptotically converge to the desired trajectories for allt∈[0,T].It can be easily shown that

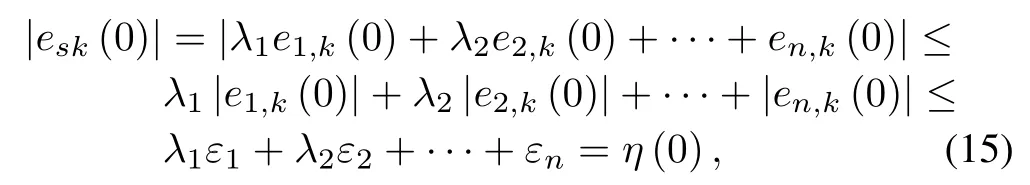
which implies thatsk(0)=esk(0)−η(0)satisfied for allk∈N.Moreover,we note the fact that

To find the approach for the controller design later,we fi rst give the time derivative ofen,k(t)as follow ing:

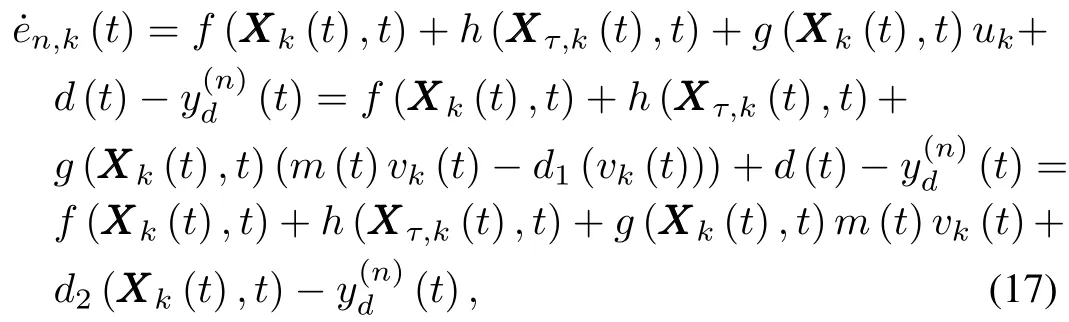
whered2(XXX k(t),t)=−g(XXX k(t),t)d1(vk(t))+d(t).From Assumptions 4 and 7,we know thatd2(XXX k,t)is bounded,i.e.,there exists unknown smooth positive function(XXX k)such that|d2(XXX k,t)(XXX k).For the simplification of expression,wedenoteg(XXX k(t),t)m(t)bygm(XXX k(t),t):=g(XXX k(t),t)m(t).It is clear that=mmingmin≤gm(xk,t)≤mmaxgmax=.

Define a smooth scalar function as

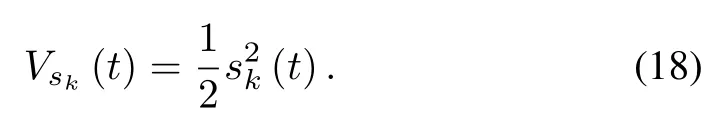
The time derivative ofVsk(t)along(17)can be expressed as

Using Young′s inequality and noting Assumption 3,it is clear that

wherea1is a given arbitrary positive constant.

Substituting(21)and(22)into(19)leads to

To overcome the design difficulty arising from the unknown time-varying delay termconsider the follow ing Lyapunov-Krasovskii functional:

According to Assumption 2,taking the time derivative ofVUk(t)leads to

Define a Lyapunov functional asVk(t)=Vsk(t)+VUk(t),taking the derivative ofVk(t)and recalling(23)and(25),we can obtain

For the convenience of expression,denoteξ(XXX k(t)):=then(26)can be simplified as

Next we need to design the controller based on(27).However,noting that there is a problem of singularity in(27)due to the termwhich approaches∞assk(t)approaches zero.In order to dealw ith this problem,we exploit the follow ing characteristic of hyperbolic tangent function.

Lemm a 1[29].For any constantη＞0 and any variablep∈R,

Employing the hyperbolic tangent function,(27)can be rew ritten as

Upon multiplication of(29)by,it becomes

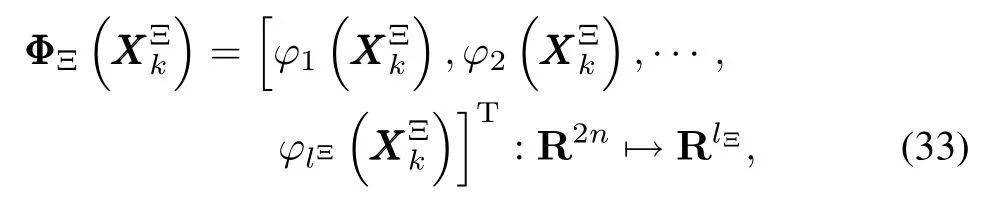
Thus,we can make the follow ing reasonable assumption.

Assum ption 8.The optimal weight vectorand(t)are bounded,i.e.,

Based on the NNsgiven by(34)and(35),we can design the adaptive iterative learning controller for the classof repeatable nonlinear system(1)as follows:

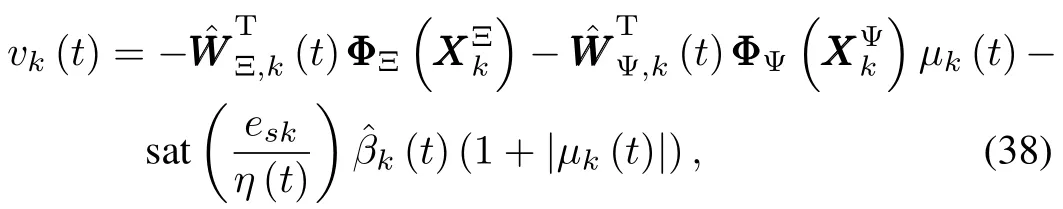
whereq1,q2,q3＞0 and 0＜γ＜1 are design parameters.In order to show how controller(38)can guarantee stability andconvergence of tracking errors later,we define the estimation error asand

Then,substituting controller(38)back into(30)yields

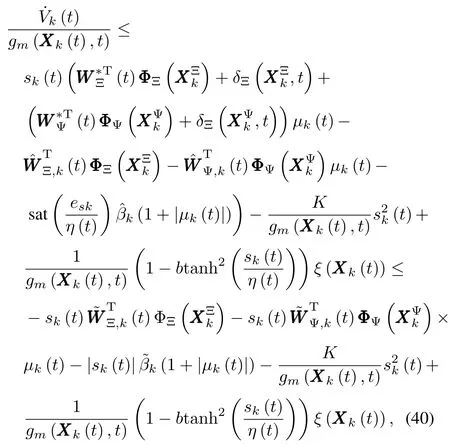
which can be rew ritten as

IV.ANALYSISOF STABILITY AND CONVERGENCE

In this section,we w ill analyze the stability of the closedloop system and the convergence of tracking errors.

The stability of the proposed AILC scheme is summarized as follows.

Theorem 1.Considering closed-loop system(1),if Assumptions 1∼8 hold,by designing control law(38)w ith adaptive updating laws(39a)∼(39c),the follow ing properties can be guaranteed.

1)A ll the signals of the closed-loop system are bounded.

2)The system tracking erroresk(t)converges to a small neighborhood of zero ask→∞,i.e.,3)limk→∞ ‖ek(t)‖ ≤(1+‖Λ‖)whereλ0andk0are positive constants and w ill be given later.

Proof.Now wew ill check the stability of the proposed controller by CEF-based analysis.Firstof all,define a Lyapunov-Krasovskii-like CEF as

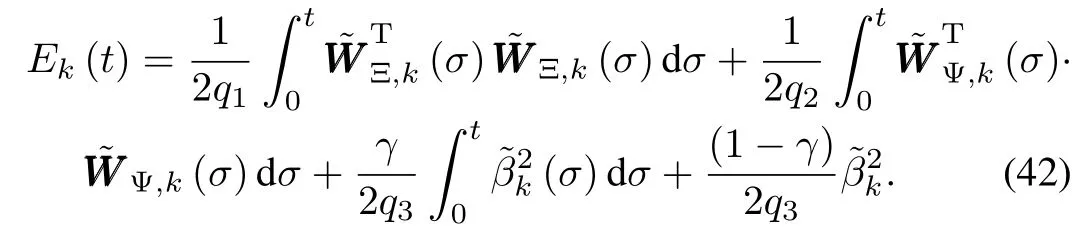
Compute the difference ofEk(t),which is

Utilizing the algebraic relation(a−b)T(a−b)−(a−c)T(a−c)=(c−b)T[2(a−b)+(b−c)]and taking the adaptive learning laws(39a)and(39b)into consideration,we have the follow ing two equalities:

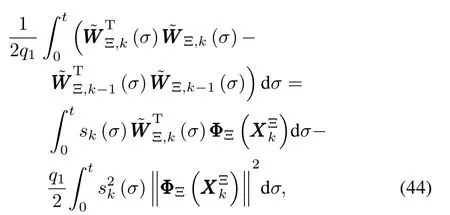
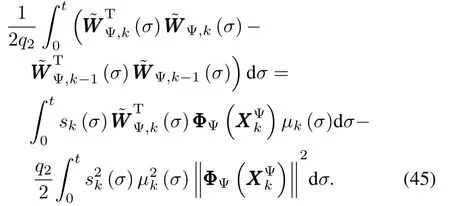
Recalling adaptive learning law(39c),the last two terms of(43)can be transformed into(46).

Substituting(44)∼(46)back into(43),it follows that

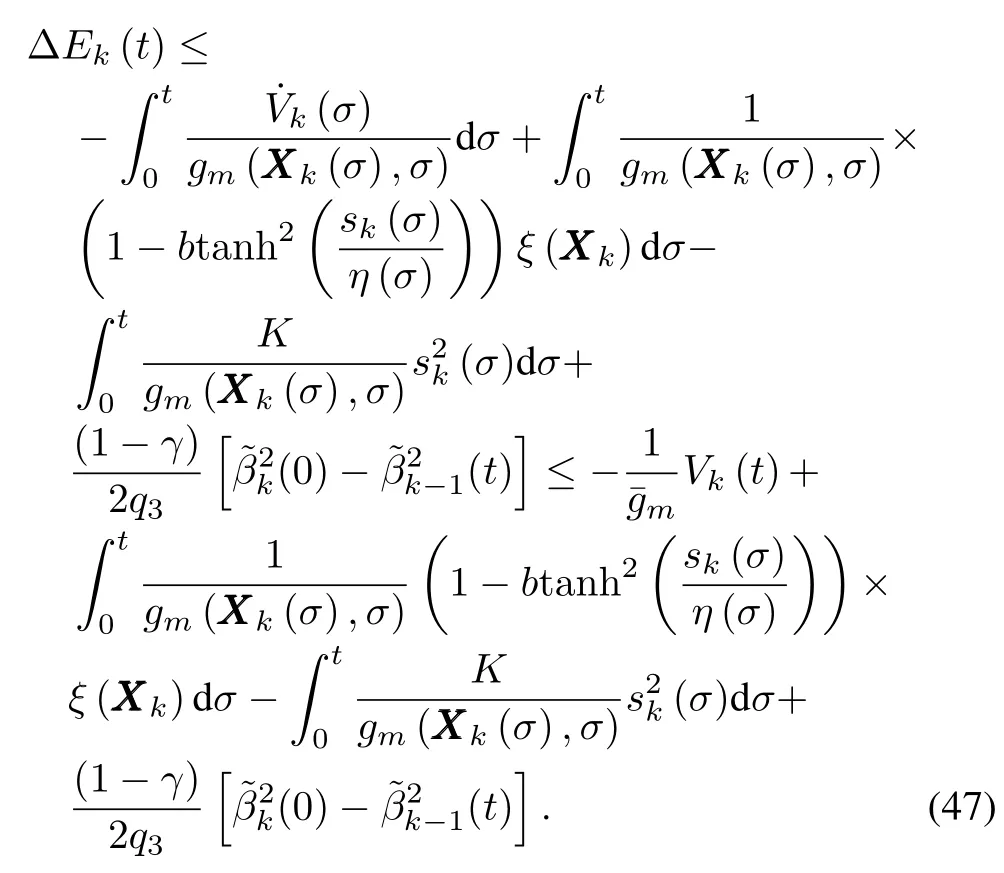
To continue the analysis,we need to exploit the follow ing property of the tangent hyperbolic function.

Lemm a 2.Consider the setΩskdefined byΩsk:=Then for anysk(t)the follow ing inequality is satisfied:

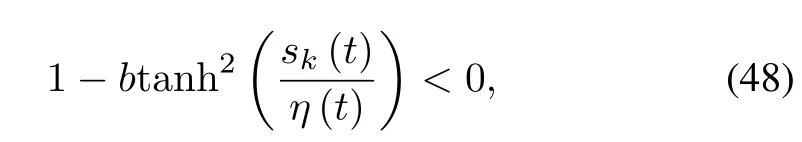
whereb＞1,m=ln

Proof.The proof is in Appendix.

For analysis of stability,we consider two cases as follows.

Case 1.sk(t)∈Ωsk.

In this case,|sk(t)|mη(t)is satisfied.Ifsk(t)=0,we knowesk(t)is bounded byη(t),i.e.,|esk(t)|η(t).Ifsk(t)＞0,we havesk(t)=esk(t)−η(t).From|sk(t)|mη(t),we can obtainsk(t)=esk(t)− η(t)mη(t)which further implies 0＜esk(1+m)η(t).Sim ilarly,ifsk(t)＜0 we havesk(t)=esk(t)+η(t)−mη(t)which implies0＞esk(t)−(1+m)η(t).Synthesizing the above discussionwe know that|esk(t)|(1+m)η(t)holds.Obviously,xi,k(t)are bounded,sinceX d(t)is bounded.From the updating laws(39a)∼(39c),we know thatΞ,k(t),Ψ,k(t)and are bounded aswell.Follow ing this chain of reasoning,the boundedness ofvk(t)can be deduced.Thus,all closed-loop signals are bounded.

Case 2.sk(t)

From Lemma 2,we know that the last term ofΔEk(t)can be removed from the analysis.Therefore,(47)can be simplified as

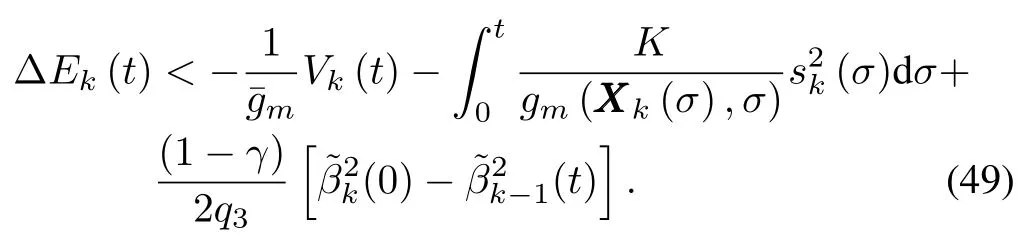
Lett=T,according toˆβk(0)=ˆβk−1(T),ˆβ1(0)=0,we have

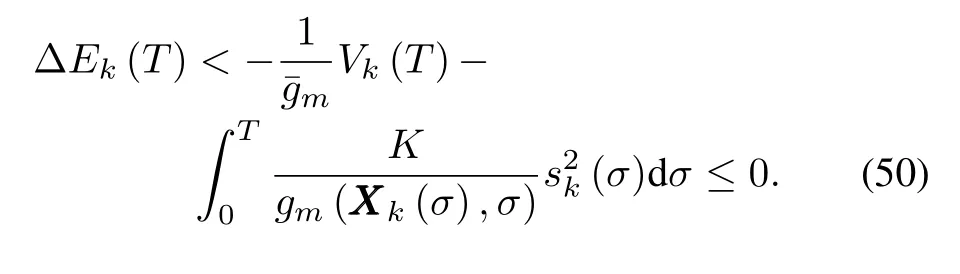
Inequality(50)shows thatEk(T)is decreasing along iteration axis.Thus,the boundedness ofEk(T)can be ensured provided thatE1(T)is finite.

According to the definition ofEk,we know

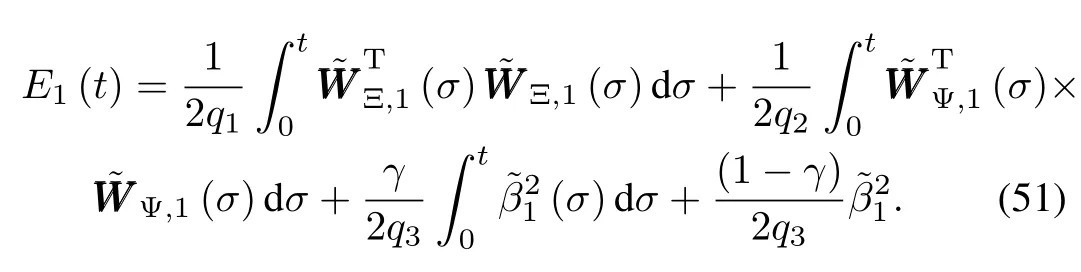
Taking the derivative ofE1(t)yields

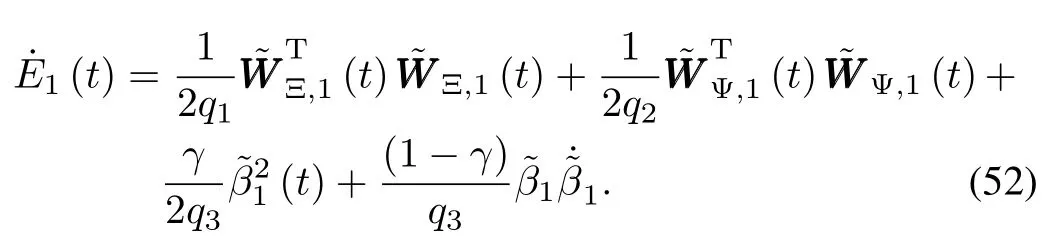
Recalling the parameter adaptive laws(39a)∼(39c),we haveq3|s1(t)|(1+|µ1(t)|),then we obtain

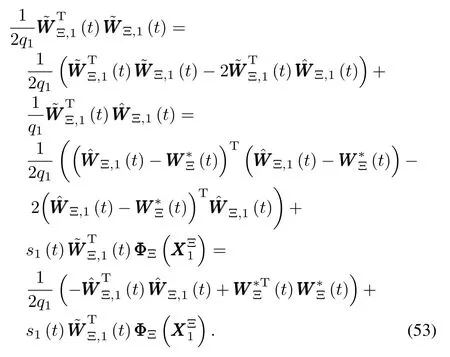
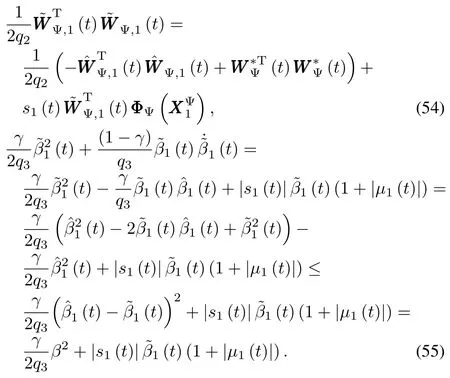
Substituting(53)∼(55)back into(52)yields

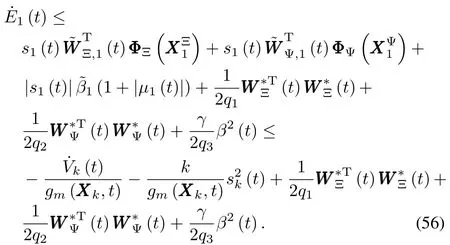
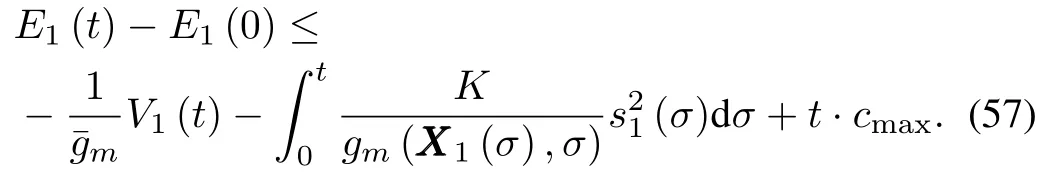
Substituting(58)back into(57)results in

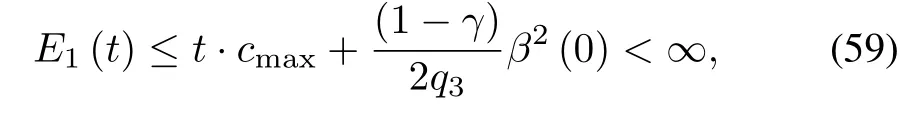
which implies the boundedness of E1(t),so Ek(t)is finite for any k∈N.Applying(50)repeatedly,we have

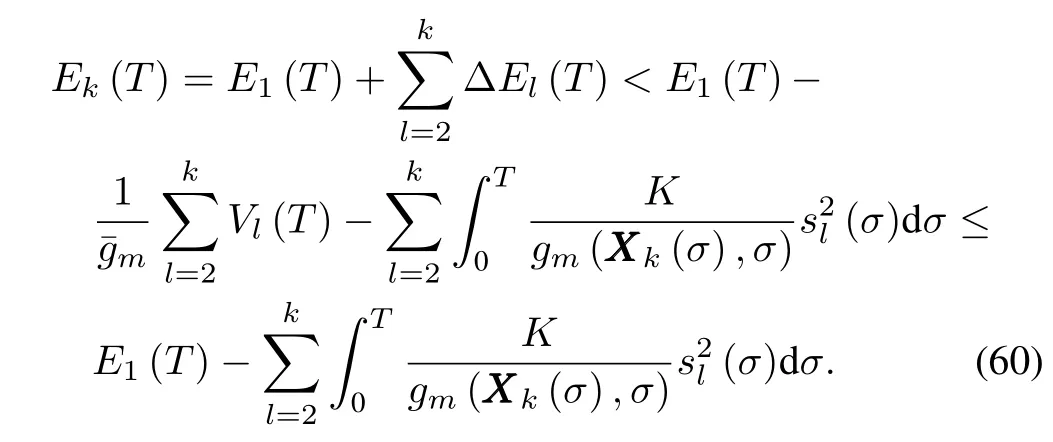
We rew rite(60)as

Taking the lim itation of(61),it follows that

Since E1(T)is bounded,according to the convergence theorem of the sum of series,0,which implies that0,.Moreover,from definition (12),we can know that lim.Furthermore,the bound ofw ill satisfy

Next we w ill prove the boundedness of the signals by induction.Firstly,we separate Ek(t)into two parts,i.e.,

The boundedness of E1n,k(T)and E2n,k(T)is guaranteed for all iterations.Consequently,∀k ∈ N,there exist finite constants M1and M2satisfying

Then,we have

On the other hand,from(49)and E2n,k+1(0)=E2n,k(T),we obtain

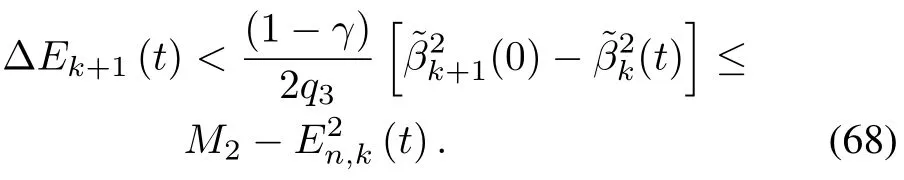
Combining(67)and(68)results in

As we have proven that E1(t)is bounded,therefore,Ek(t)is finite.Furthermore,we can obtain the boundedness ofΞ,k(t),Ψ,k(t)and(t).From,we can get the boundedness of sk(t),which further implies that xi,k(t)(i=1,2,···,n)are bounded.As a result,we can obtain that vk(t)is bounded.

It is clear that,for two cases,the proposed controlalgorithm is able to guarantee that all closed-loop signals are bounded and limk→∞|esk(t)|≤(1+m)η(t).Therefore,the control objective is achieved,i.e.,limk→∞(esk(σ))2dσ ≤ εesk,

Defineζk(t)=[e1,k(t),e2,k(t),···,en−1,k(t)]T,then a state representation ofesk(t)=£ΛT1⁄ek(t)can be expressed as

where

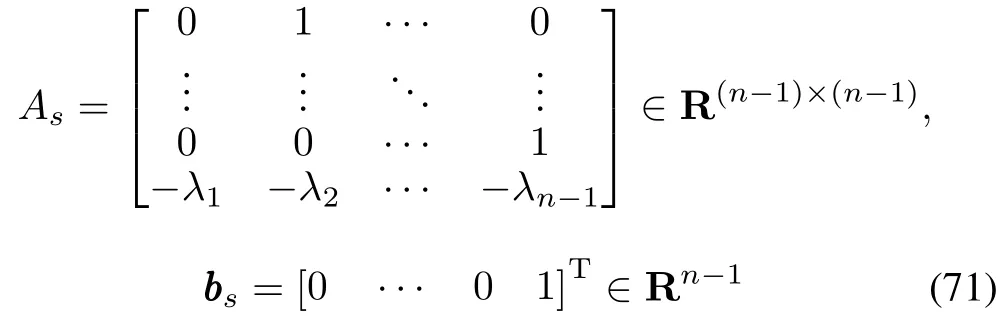
w ithAsbeing a stable matrix.In addition,there are two constants[30]k0＞0 andλ0＞0 such that‖‖eA s t‖‖≤k0e−λ0t.The solution for˙ζk(t)is

Consequently,it follows that

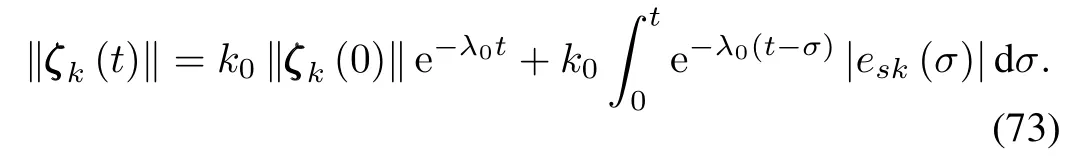
When we choose suitable parameters such thatλ0＞K,from limk→∞|esk(t)|≤(1+m)η(t),we can have

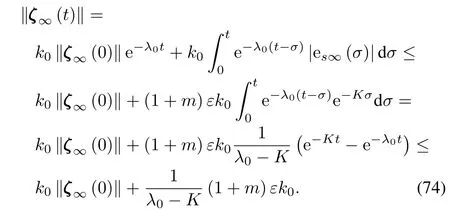
Considering the two inequalities above,we can obtain

The third property of Theorem 1 can be concluded.Moreover,from the boundedness ofX k(t)andX d(t)we know there exists a compact setΩ=supk∈N{X k(t),X d(t)}on which the NNs approximate uncertainties.

This concludes the proof.

V.SIMULATION STUDY

In this section,a simulation study is presented to verify the effectiveness of the proposed AILC scheme.Consider the follow ing second-order nonlinear system w ith unknown timevarying delays and unknown dead-zone running over[0,4π]repetitively:

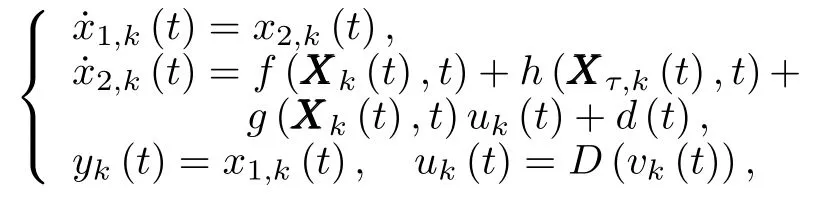
wheref(X k(t),t)=−x1,k(t)x2,k(t)sin(x1,k(t)x2,k(t)),g(X k(t),t)=¡0.9+0.1|cos(2t)|2sin2(x1,k x2,k)¢,h(Xτ,k(t),t)=0.2 sin(t)e−|cos(2t)|(x1,k(t− τ1(t))×sin(x1,k(t− τ1(t)))+x2,k(t− τ2(t))sin(x2,k(t− τ2(t)))),d(t)=0.1sin(t),the time delays areτ1(t)=0.5(1+sint)andτ2(t)=1−0.5 cos(t)w ithτ1max=1,1≤0.5 andτ2max=1.5,2≤ −0.5.We give the simulation study in the follow ing four cases.

Case 1.The desired trajectory to be tracked by the state vector is given byX d(t)=[sint,cost]T.The design parameters are chosen asε1=ε2=1,λ=2,K=3,γ=0.5,q1=q2=1,q3=0.01,ε=λε1+ε2=3.The parameters for dead-zone are specified bym=1+0.2sint,br=2,bl=−2.The parameters for NNs are chosen aslΞ=30,=[2,3,1,1.5],=2,and[2,3],σΨj=2,j=1,2,···,lΨ.The initial conditionsx1,k(0)andx2,k(0)are random ly taken in the intervals of[−0.5,0.5]and[0.5,1.5],respectively.Parts of the simulation results are shown in Figs.2∼6.

Case 2.To show the control performance formore complicated desired trajectory,we choose the desired trajectory asXXX d(t)=[sint+sin(2t),cost+2 cos(2t)]T.The design parametersare chosen the same as those in Case 1.The initial conditions ofx1,k(0)andx2,k(0)are random ly taken in the intervalsof[−0.5,0.5]and[2.5,3.5],respectively.Partsof the simulation results are shown in Figs.7∼11.

As shown in simulation figures,we can see that the proposed controller can also achieve good performance formore complicated desired trajectory.

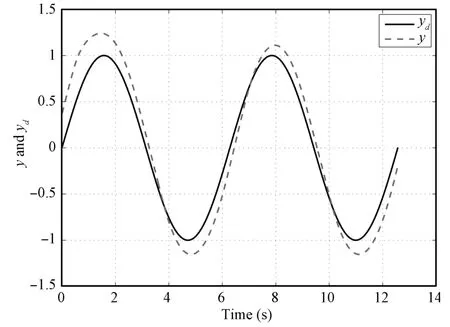
Fig.2. System output y and desired trajectory yd(k=1)in Case 1.

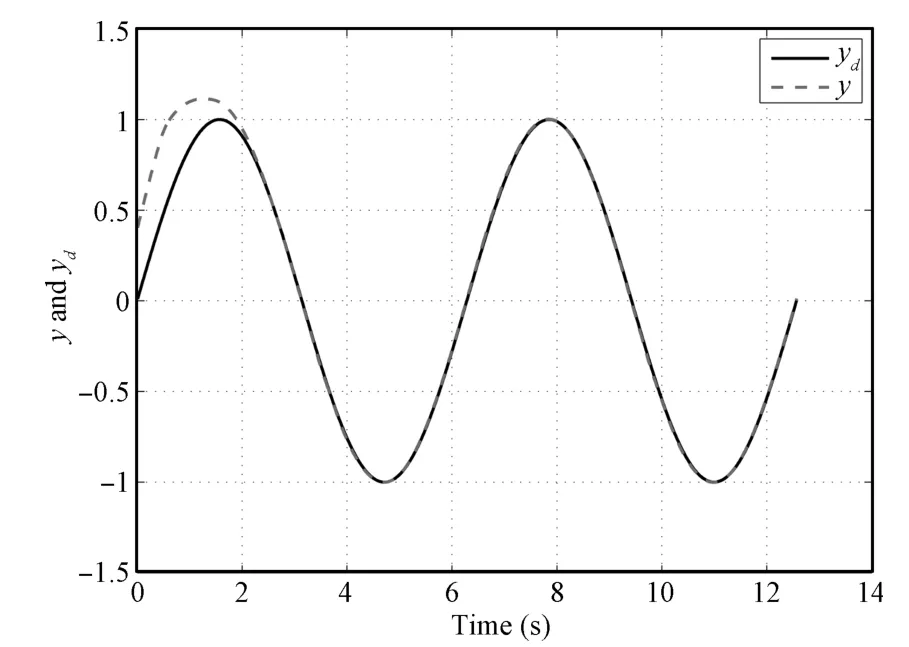
Fig.3. System output y and desired trajectory yd(k=5)in Case 1.

Case3.To study the controlperformanceof differentdesign parameters,the following case is investigated.The desired trajectory is the same as in Case 2.The parameters are chosen asλ=3,K=4,γ=0.5,q1=q2=2,q3=0.02,ε=λε1+ε2=4 w ith all other parameters fixed.The initial conditionsx1,k(0)andx0,k(0)are also random ly taken in the intervals of[−0.5,0.5]and[2.5,3.5],respectively.Due to space reasons,we only give the results ofdtversus thenumberof iterations in this case.Comparing Fig.12 w ith Fig.11,it shows that fast adaption may improve the convergence rate in terms of iteration times.

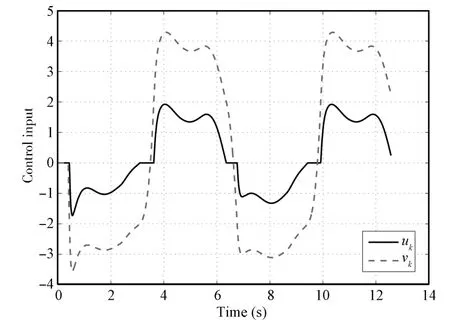
Fig.4. Control input uk and vk(k=1)in Case 1.

Case4.Finally,the contribution of this paper is shown by comparing the proposed controller w ith traditional adaptive NN controller[30].The controller is the same,but the adaptive laws usingσ-modification for parameters are given by

Fig.5. Control input uk and vk(k=5)in Case 1.

Fig.6. (t)d t versus the number of iterations in Case 1.

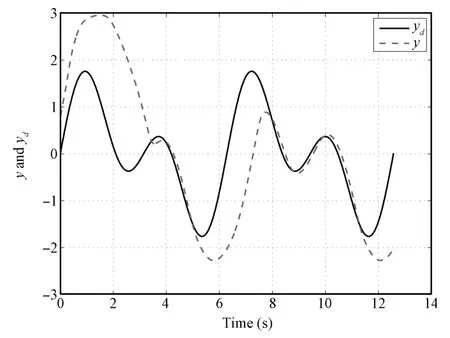
Fig.7. System output y and desired trajectory yd(k=1)in Case 2.

Fig.8. System output y and desired trajectory yd(k=15)in Case 2.

The design parameters are given byσ1=σ2=0.5,γ=0.5,q3=0.02.Astraditional adaptive NN controller runs in time domain,the notation k in this case does not have any practicalmeaning.Figs.13 and 14 providesimulation results.From thesimulation results shown below,it is obvious that the adaptive NN controller performsmuch worse than the proposed approach.

As observed in the simulation results above,the proposed AILC can achieve a good tracking performance,and tracking errors decrease along the iteration axis,which demonstrates the validity of the AILC approach proposed in this paper.

Fig.9.Control input uk and vk(k=1)in Case 2.

V I.CONCLUSIONS

In this paper,a RBF NN-based AILC scheme is proposed for a class of nonlinear time-varying systems w ith unknown time-varying delays and unknown input dead-zone nonlinearity running over a finite time interval repetitively.A novel representation of the dead-zone output is given.Using appropriate Lyapunov-Krasovskii functional in the Lyapunov function candidates,the uncertainties from unknown timevarying delays are removed such that control law is delayindependent.The identical initial condition for ILC has been relaxed by introducing the boundary layer.The hyperbolic tangent function is employed to avoid the problem of possible singularity.RBF NNs are then introduced to compensate for the uncertainties of system.Theoretical analysis by constructing Lyapunov-like CEF has shown that the tracking errors converge to a small residual domain around the origin as iteration number goes to infinity.At the same time,all the closed-loop signals remain bounded.Simulation results have been provided to show the effectiveness of the proposed control scheme.However,in this paper,we only study the systems in Brunovsky form.In futurework,wew ill investigate to apply the proposed approach to more general systems.

APPENDIX

ProofofLemma2.LetInequality(42)can be expressed as

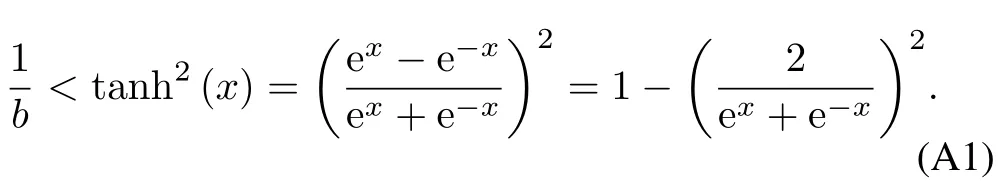
Since exand e−xare positive,we know

Further,we can obtain

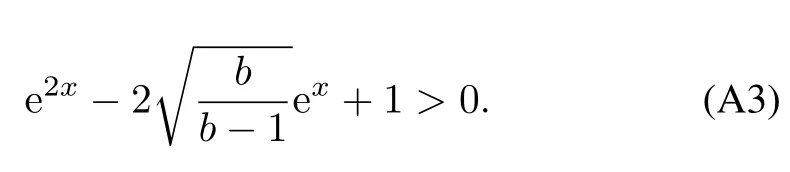
Solving the quadratic inequality(A.3),we get

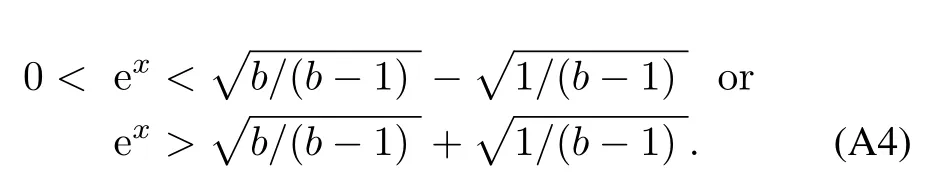
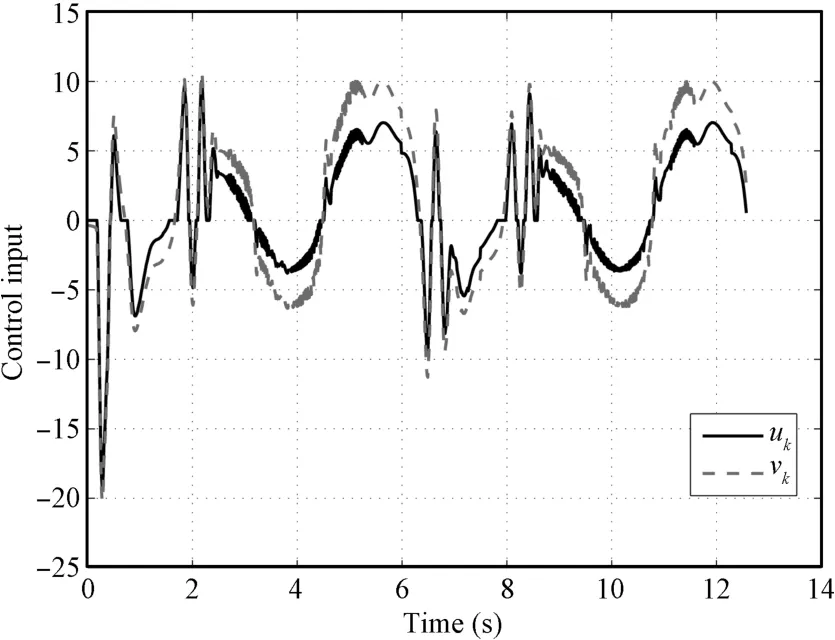
Fig.10.Control input uk and vk(k=15)in Case 2.

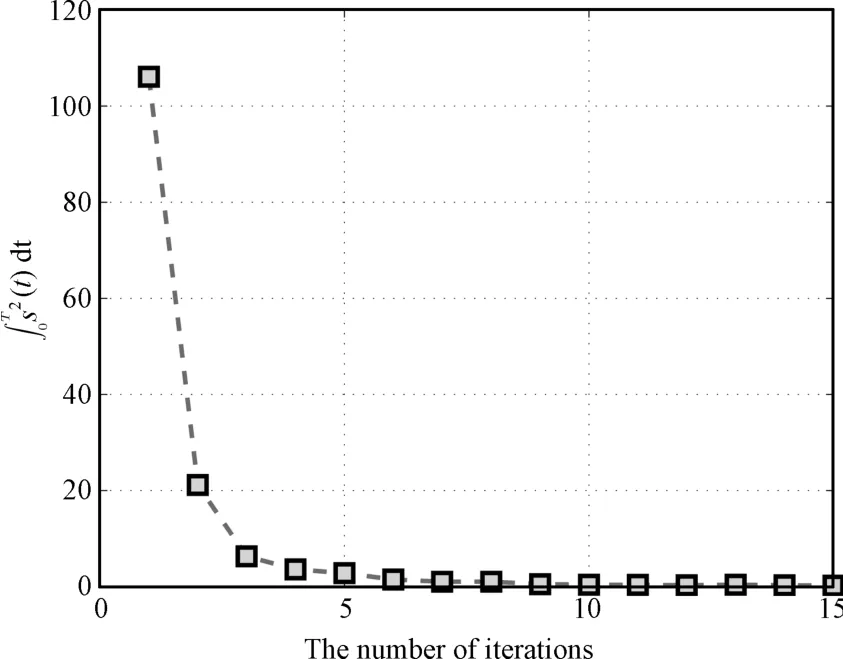
Fig.11.∫T0 s(t)d t versus the number of iterations in Case 2.

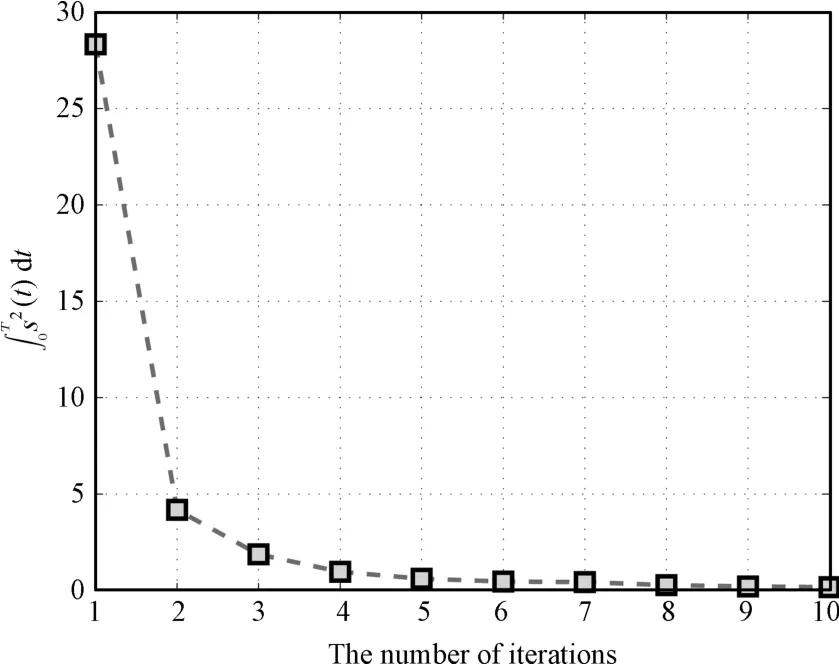
Fig.12. ∫T0 s(t)d t versus the number of iterations in Case 3.

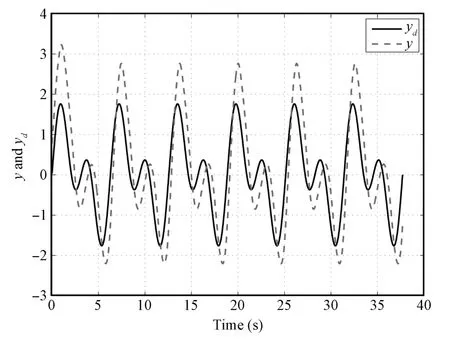
Fig.13. System output y and desired trajectory yd in Case 4.

Fig.14. Control input uk and vk in Case 4.

On the other hand,from|sk(t)|＞mη(t)we know

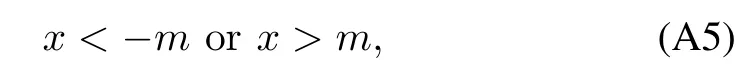
which implies

Obviously,Lemma 2 holds.□

[1]Arimoto S,Kawam rua S,M iyazaki F.Bettering operation of robots by learning.JournalofRobotic System,1984,1(2):123−140

[2]Kuc T Y,Nam K,Lee J S.An iterative learning control of robot manipulators.IEEE Transactions on Robotics and Automation,1991,7(6):835−841

[3]Jang T J,Choi C H,Ahn H S.Iterative learning control in feedback systems.Automatica,1995,31(2):243−248

[4]Sun M X,Wang D W.Iterative learning control w ith initial rectifying action.Automatica,2002,38(7):1177−1182

[5]Chien C J,Liu J S.A P-type iterative learning controller for robust output tracking of nonlinear time-varying systems.International Journal ofControl,1996,64(2):319−334

[6]Hou Zhong-Sheng,Xu Jian-Xin.A new feedback-feedforward configuration for the iterative learning control of a class of discrete-time systems.Acta Automatica Sinica,2007,33(3):323−326(in Chinese)

[7]French M,Rogers E.Non-linear iterative learning by an adaptive Lyapunov technique.International Journal of Control,2000,73(10):840−850

[8]Choi JY,Lee JS.Adaptive iterative learning controlof uncertain robotic systems.IEEProceedingson Control Theory Application,2000,147(2):217−223

[9]Xu JX,Tan Y.A composite energy function-based learning control approach fornonlinear systemsw ith time-varying parametric uncertainties.IEEE Transactionson Automatic Control,2002,47(11):1940−1945

[10]Tayebi A.Adaptive iterative learning control for robot manipulators.Automatica,2004,40(7):1195−1203

[11]Xu J X,Tan Y,Lee T H.Iterative learning control design based on composite energy function w ith input saturation.Automatica,2004,40(8):1371−1377

[12]Chi Rong-Hu,Sui Shu-Lin,Hou Zhong-Sheng.A new discrete-time

adaptive ILC for nonlinear systemsw ith time-varying parametric uncertainties.Acta Automatica Sinica,2008,34(7):805−808(in Chinese)

[13]Chi R H,Hou Z S,Xu JX.Adaptive ILC for a class of discrete-time systems w ith iteration-varying trajectory and random initial condition.Automatica,2008,44(8):2207−2213

[14]Chien C J.A combined adaptive law for fuzzy iterative learning control of nonlinear systems w ith varying control tasks.IEEE Transactions on Fuzzy Systems,2008,16(1):40−51

[15]Wang Y C,Chien C J.Decentralized adaptive fuzzy neural iterative learning control for nonaffine nonlinear interconnected systems.Asian JournalofControl,2011,13(1):94−106

[16]Ge SS,Hong F,Tee T H.Robustadaptive control of nonlinear systems w ith unknown time delays.Automatica,2005,41(12):1181−1190

[17]Hua C C,Feng G,Guan X P.Robust controller design of a class of nonlinear time delay systems via backstepping method.Automatica,2008,44(2):567−573

[18]Chen W S,Jiao L C,Li J,Li R H.Adaptive NN backstepping output-feedback control for stochastic nonlinear strict-feedback systems w ith time-varying delays.IEEE Transactions on Systems,Man and Cybernetics-PartB:Cybernetics,2009,40(3):939−950

[19]Chen W S.Novel adaptive learning control of linear systems w ith completely unknown time delays.International Journal of Automation and Computing,2009,6(2):177−185

[20]Chen W S,Zhang L.Adaptive iterative learning control for nonlinearly parameterized systemsw ith unknown time-varying delays.International JournalofControl,Automation and Systems,2010,8(2):177−186

[21]Chen Wei-Sheng,Wang Yuan-Liang,Li Jun-M in.Adaptive learning control for nonlinearly parameterized systems w ith periodically timevarying delays.Acta Automatica Sinica,2008,34(12):1556−1560(in Chinese)

[22]Tao G,Kokotovic P V.Adaptive control of plantsw ith unknown deadzones.IEEE Transactionson Automatic Control,1994,39(1):59−68

[23]Wang X S,Hong H,Su C Y.Model reference adaptive control of continuous-time systems w ith an unknown input dead-zone.IEE Proceedingson Control Theory Applications,2003,150(3):261−266

[24]Tang X D,Tao G,Suresh M J.Adaptive actuator failure compensation for parametric strict feedback systems and an aircraft application.Automatica,2003,39(11):1975−1982

[25]Wang X S,Su C Y,Hong H.Robust adaptive control of a class of nonlinear systems w ith unknown dead-zone.Automatica,2004,40(3):407−413

[26]Zhang T P,Ge S S.Adaptive neural control of M IMO nonlinear statetime-varying delay systems w ith unknown dead-zones and gain signs.Automatica,2007,43(6):1021−1033

[27]Zhang T P,Ge S S.Adaptive dynam ic surface control of nonlinear systems w ith unknown dead zone in pure feedback form.Automatica,2008,44(7):1895−1903

[28]Xu J-X,Xu J,Lee T H.Iterative learning control for systems w ith input deadzone.IEEE Transactions on Automatic Control,2005,50(9):1455−1459

[29]Ge S S,Lee K P.Approximation-based control of nonlinear M IMO time-delay systems.Automatica,2007,43(1):31−43

[30]Ioannou P A,Sun J.Robust Adaptive Control.Englewood Cliffs,NJ:Prentice-Hall,1995.