Reinforcement Learning Transfer Based on Subgoal Discovery and Subtask Similarity

Hao Wang Shunguo Fan Jinhua Song Yang Gao Xingguo Chen

I.INTRODUCTION

I N recent decades,there has been an increasing research interest in reinforcement learning(RL).In the field of machine learning,RL isan important category thatspecializes in a large class of learning problems[1].RL methodology(partly)originates from the biological observation that,the intention of perform ing some action under some circumstance can be reinforced or restrained by external stimulating signals.Well-supported by dynam ic programming techniques,many RL algorithms were developed in the early 1990s,among which Q-learning,Sarsa,etc.aremost popular[1].

Although it is very successful in various learning tasks,nowadays RL suffers from the low speed of learning in certain tasks.Such tasks typically have relatively large problem space,and as a consequence the conventional RL updating strategies become less efficient or even infeasible.Despite of those efforts in developing more advanced RL algorithms(such as function approximation techniques,hierarchical RL,etc.),the methodology of transfer learning has recently attracted much attention.

W ithout any specific context,transfer learning refers to the general idea that past learning experiencemay be and should be used to aid future learning.When applied to RL,transfer learning becomes concrete problems such as how to reuse previously learnt results(for example,policies,i.e.,the way of behaving under various states)or intermediate know ledge(for exampleV-values,which are quality indicators of states).From a broader point of view,such questions include also,for example,among many previous tasks how to extract the specific know ledge from the most appropriate task to help current learning.Such questions have been open since the late 1990s.During the past decade,lots ofmethods for inter-task transfer learning in RL havebeen proposed to provide different answers to the questionsabove[2−7].Wew ill summarize these works in Section II.

In this paper,we provide our solution to the abovementioned problems.From a systematic point of view,our method aims atmaintaining a library of those reusable units collected from past learning tasks.Then,upon learning a new task,we attempt to use the library whenever it is possible and beneficial to do so.In order to search the library for a piece of know ledge to transfer,we define a similaritymeasure between options,of which the formal definition w ill be introduced in Section II-B.Our transfer learning method contains four stages.Firstly,in the subgoal discovery stage,we extract subgoals from learning tasks.Briefl y speaking,a subgoal is some important state during the process of accomplishing the learning task.Secondly,in the option construction stage,we construct options from the subgoals.An option can be considered as the guideline from one subgoal to another.Hence several options togethermay guide the learner to fulfi ll the learning task quickly.Thirdly,in the similarity search stage,for a given target task,we search the library for the best option.To this end,we propose a novel sim ilarity measure which is built upon the intuition that similar options have sim ilar state-action probability.Finally,in the option reusing stage,the best option found in the sim ilarity search stage is reused to speed up the current learning task.Comparing to those existing methods,our method has the follow ing advantages.

1)Our proposed method imposes lim ited constraint on the tasks,thus it isw idely applicable;

2)The basic reusable unit in ourmethod is small,thus one target task can benefi t from multiple reusable units;

3)Our proposed method is an automatic method that does not require any human intervention.Itworks as a system that automatically maintains the reusable source library.

The rest of the paper is organized as follows.After a brief introduction of necessary background know ledge in Section II.Section III introduces our proposed transfer learningmethod,aswell as the sim ilarity measure between options.In SectionIV,we examine our proposed method by extensive experiments.Then,Section V summarizes existingmethods thatare closely related to ourwork.Finally,Section VI concludes the paper and points out possible future directions.

II.BACKGROUND

A.RL and Markov Decision Process(MDP)

RL isa classof learning techniques characterized by a class of learning tasks[1].Such learning tasks can be wellmodeled as Markov decision processes(MDPs).A finite MDPMis a four-tuple,M=〈S,A,T,R〉whereSis the finite set of states;Ais the finite set of actions;T:S×A×S→[0,1]is the transition probability;andR:S×A×S→is the reward function.For example,when making an agent learn how to escape from amaze,the reward is often zero until it escapes.A learning agent can actively surf w ithin the state space.Assume that at timetthe agent is in statest.Itmay take one of the available actions inst,say,at∈A,and itw ill be transported into another statest+1∈Sw ith probabilityT(st,at,st+1).A fter the transportation,the agent receives a reward ofrt=R(st,at,st+1).

W ithin such an environment,a reinforcement learner aims at finding an optimalway of behaving,i.e.,an optimal policywhereis the probability distribution over the action spaceA,such that w iththe follow ing expected return w ill bemaxim ized

whereγis the discounting factor.rtakes values from the interval(0,1)and in our experiments the immediate rewardsrt+τ+1∈{0,1}so that the convergence ofRtcan be guaranteed.

Q-learning algorithm.In practice,one of themost famous RL algorithms is Q-learning[1,8].Q-learning maintains and updates the expected discounted returnQ(s,a)for alls∈Sanda∈A.Roughly speaking,the valueQ(s,a)reflects how w ise it is to take actionain states.After actionatbeing taken in statest,Q-learning updates the Q-matrix using the follow ing rule:

A lgorithm 1 presents the Q-learning algorithm,in which a learning episode refers a complete process that,starting from the initial state,the learning agent manages to achieve the term inal state.

A lgorithm 1.Q-learning

Q=Q-LEARNING(M,N,†)

Input.M=〈S,A,T,R〉is a learning task,Nis the number of learning episodes;†∈(0,1)is a small positive threshold

Output.Q(s,a)values for alls∈Sanda∈A

1)InitializeQ(s,a)arbitrarily

2)forNlearning episodes do

3)t←0▷s0is the initial state

4)whilestis not term inal do

5)Take actionatusing the†-greedy policy

6)Observe the rewardrt+1and the next statest+1

7)UpdateQ(st,at)using(1)

8)t←t+1

9)returnQ

The†-greedy action selection policy at Line 5)is to select the“best”action w ith probability 1−†and select a random action w ith probability†.That is

Q-learning is proven to converge to theoptimalpolicy under standard stochastic approximation assumptions[8].

A lgorithm Sarsa.Another w idely-used RL algorithm is Sarsa[1,9].Sarsa is sim ilar to Q-learning.The difference is that,instead of using themaximum Q-values,Sarsa directly uses the Q-values of those(st+1,at+1)pairs.Precisely,the update rule of Sarsa is

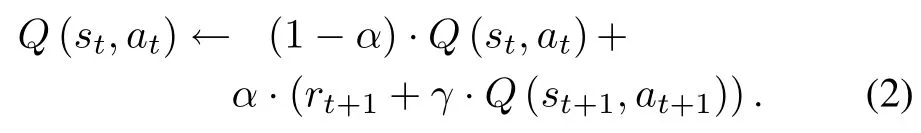
Algorithm 2 presents thisSarsa learningmethod.Q-learning and Sarsa w ill later be used in our experiments.

A lgorithm 2.Sarsa

Input and output are the same as in Algorithm 1

1)InitializeQ(s,a)arbitrarily

2)forNlearning episodes do

3)t←0▷s0is the initial state

4)Select actionatusing the†-greedy policy

5)whilestis not term inal do

6)Take actionat;observert+1andst+1

7)Select actionat+1using the†-greedy policy

8)UpdateQ(st,at)using Formula 2

9)t←t+1

10)returnQ

B.Options and Semi-Markov Decision Process SMDP

Q-learning in its original form works on the finest granularity of the state-action space,i.e.,it focuses on every individual state-action pair.However practical problems often exhibit hierarchical structures and taking advantage of such hierarchies can often yield a significant gain in efficiency.Such an idea has been extensively studied under the topic of optionsand sem i-Markov decision processes(SMDPs)[10].The concept of option is an extension to that of primitive action.Formally,an option in MDPM=〈S,A,T,R〉is defined as a tripleto=〈I,,β〉,whereI⊆Sis the set of states in which the option can be initiated,is the policy during the execution of the option,andβ:S→[0,1]is the term ination condition defining the probability w ith which the option terminates in a given states.Roughly speaking,an option can be viewed as a stored procedure that,when triggered,leads the agent into certain term ination state(s).

SMDP is the extension of MDP w ith options.We omit the formal definition of SMDP here because it would be a distraction from our main focus in this paper.Nonetheless,the updating rule for learning SMDP isuseful in our proposed method and thus is presented below

herekis the time duration of optionot.It is clear that(3)extends(1)in a naturalway.

C.Transfer Learning and Our Problem

Transfer learning in general refers to any technique thatuses past learning experience to speed up future learning.In this paper,we let this term refer to the technique that reuses learnt MDPs to speed up the learning in a new MDP.In this sense,an MDP is also a learning task.We w ill use these two terms interchangeably throughout the paper.Now we can formally describe the problem studied in this paper as follows.

Problem definition.Given a libraryLof source tasks,M1,M2,···,M n,and a target taskM,our goal is to accelerate the reinforcement learning onMby reusing know ledge extracted fromL.Especially,in this paper we require in addition that all source tasks and the target task share the same action set.

It should be noted that requiring all tasks to have the same action set does not comprom ise the generality of the problem very much.In fact,the constraintwe impose on the problem naturally emerges from many practical learning tasks.For example,in a 2D maze game,the actions of an agent are always(typically)up,down,left,and right,regardless of the detailed maze structure(i.e.,the state space).

III.OUR METHOD

In this section,we present our four-stage method for the learning task.We fi rstmanage to extracta setof localsubgoals(i.e.,key states)from a source task(Section III-A).Then,we transform these local subgoals into reusable options(Section III-B).After that,on learning the target task,we manage to identify a setof states(or state-action pairs)forwhich some of those reusable optionsmay be applied(Section III-C).Finally,we show how to use the reusable options to accelerate the learning(Section III-D).

Comparing to existingmethods,ourmethod has the following advantages:

1)Our proposedmethod only requires that theaction setsbe the same,and impose no lim itation on the state sets,transition probabilities,or reward functions,and thus the method is w idely applicable in various transfer learning scenarios.

2)The basic reusable units in our proposed method are options,which are,briefly speaking,fractional policies extracted from the source tasks.Therefore the target task can reusemultiple options and gain a significant acceleration.

3)Our proposed method is an automaticmethod that does not require any human intervention.Especially,it automatically discovers subgoals in the task library aswell as the best matching between the target task and the reusable options.

A.Discovery ofSubgoals

The subgoal discovery phase in our proposed method aims at extracting a set of subgoals from the source library.Currently there are two classes of strategies that serve for this purpose.One is to use the frequency of states[11],and theother is to use thegraphmodel[12].Although theymay achievegood performance in accuracy,methods based on graphmodels are typicallymuchmore time-consuming,and thusarenotsuitable for large MDPs.Hence in this paper we consider the state frequency as the indicator of subgoals.The rationale comes from the intuition that if a state is visited frequently then it is important and vice versa.(For example,imagine if there is a single state bridging two disjoint parts of the state space.)

However it is reported that frequency-based methods are sensitive to noise[13],which eventually harms the accuracy.Also,existing frequency-basedmethodsmerely take theglobal perspective of a state,i.e.,they only consider those statesw ith globally highest frequencies.In this paper,we argue that an effective method should take advantage of both global and local perspectives.The idea is that if a state hasa significantly higher visiting frequency than its neighbors then it should be regarded as important w ithin its own neighborhood.We call such kind of states local subgoals.One may think of such local subgoals as the“entries”of traffi c crosses in an MDP or“bridges”that connect different state subspaces.

To find all the local subgoals,we adopt a connection-based method[14].Specifically,given an MDPM=〈S,A,T,R〉and statess,s′∈S,we define

whereC(·)provides the visiting frequency.Briefl y speakingδ(s,s′)measures the“exceeded”visiting frequency from statesto states′.Then,we measure the eligibility of a statesbeing a local subgoalby summ ing up all the exceeded visiting frequencies fromsto its neighbors,weighted by the transition probability,as shown in(5)

Then we can give the definition of the relative subgoals.

Statesw ith highΔ-values are those local subgoalswe look for.Formally,given an MDPM=〈S,A,T,R〉and an integer thresholdk,a states∈Sis a local subgoal if it satisfies the follow ing two conditions:

1)s∈topk(S),where topk(S)is the set ofkstates that have the large P stΔ-values;

Condition 1 guarantees that a local subgoal is also globally“notbad.”Condition 2 says that the quality of a local subgoal should be larger than the quality of itsneighbors.In a concrete situation,for example a maze game,this condition in fact says that when two bottleneck states are adjacent,then it is suffi cient to take only one of them as a local subgoal,and therefore the set of extracted local subgoals is constrained w ithin a reasonable size.

It remains to be clarified thathow to obtain all the frequenciesC(·)as well as the state-action probability Pr{·|s}.In general,when positioned in an unknown environment,an agent w ill need excessive exploration of the environment,and then itw ill be able to distinguish bottlenecks and“regular”states.Based on this idea,we use a Monte Carlo sampling process to estimate the frequencies.We let the agent explore the environment(using an RL algorithm such as Q-learning)forNepisodes,whereNis a parameter related to the complexity of the environmentand the expected running time.During the exploration,we collect all the non-circular trajectories from the starting state to the term ination state.We then count,for each states,how many timessappears in these trajectories,and use the number of appearance as the estimation ofC(s).Pr{·|s}can also be estimated by counting the frequency ofdifferent actions in states.The reason why we focus on non-circular trajectories is that,comparing to very complex trajectories w ith cycles,non-circular trajectories correspond to simpler(and thus better)ways to travel from the starting state to the term ination state.

A lgorithm 3 summarizes the procedure of subgoal discovery.Note that in addition to the setof subgoals,G,Algorithm 3 also produces the setJof successfulnon-circular trajectories in the task MDPM.We shall use this setJin the upcom ing phase of option construction.

A lgorithm 3.Subgoal discovery

(G,J)=SUBGOALDISCOVERY(M,N,k)

Input.M=〈S,A,T,R〉is a learning task;Nandkare two integer thresholds

Output.1)G,local subgoals inM;2)J,successful non-circular trajectories

1)Use an RL algorithm(e.g.,Q-learning)to learnMforNepisodes;record all successful non-circular trajectories inJ

2)for eachs∈Sdo

3)Estimate the state frequencyC(s)by counting the number of appearance ofsinJ

4)Estimate state-action probability Pr{·|s}

5)for eachs∈Sdo

6)ComputeΔ(s)according to(4)and(5)

7)for eachs∈Sdo

10)then addsintoG

11)returnG,J

B.Construction ofOptions

We now construct reusable options using those discovered local subgoals.Basically,we construct options in such a way that every option can be thought of as a“guiding policy”towards some subgoal,and thus when reused,itmay help to accelerate the learning process.

Algorithm 4 summarizes the procedure of option construction.The procedure begins w ith extracting all the subtrajectories fromJ,such that the starting state and the ending stateofeach sub-trajectory areboth subgoals Lines1∼4.Note that such sub-trajectories correspond to(probably suboptimal but feasible)policies that guarantee the accomplishment of subgoals.Then,for each sub-trajectory we construct one option(Lines 5∼10).Specifically,the initial setIis the set of all the states along the sub-trajectory except for the termination subgoal(Line 7).The policyπof the option is simply the sub-trajectory itself,i.e.,follow ing the subtrajectory to the terminating subgoal(Line 8).Finally,each option is further learnt in its own MDPMfor optimal Q-values of the term ination subgoal(Lines 11 and 12).In this way,all the options are now ready to be transferred.

A lgorithm 4.Option construction

O=OPTIONCONSTRUCTION(G,J)

Input.GandJare the sets of subgoals and trajectories,respectively,of some underlying taskM,they are the outputsof Algorithm 3 w ith the inputM.

Output.O,a set of options

1)W←Ø

2)for each trajectoryξ∈Jdo

3)FindWξ,the setof segmentsofξwhere eachw∈Wstarts w ith some subgoalg∈Gand endsw ith another subgoalg′∈G

4)AddWξintoW

5)for each segmentw∈Wdo

7)I←{s1,s2,···,sk−1}

8)fori=1,2,···,k−1 do(si)←ai

9)β←{sk}

10)Add optiono← 〈I,,β〉intoO

11)for each optiono=〈I,,{s}〉∈Odo

12)LearnMfor optimal Q-valuesQ(s,a)(∀a∈A)

13)returnO

C.Option Similarity

As isexplained before,upon learning anew task wewant to reuse those optionswe obtained from source tasks.To do this,our basic idea is that we fi rst let the learning agent explore the environment for awhile,identifying a setof subgoals and constructing options,aswhatwe have done for all the source tasks(see Section III-A and III-B).Then,sincewe have learnt theoptimalQ-values forall theoptions in the source tasks(see Line 12 of Algorithm 4),we can reuse the optimal Q-values of a source optionoif it is“sim ilar”to some target optiono′.Intuitively,such reused Q-values could be a good“initial guess”for further optimization.The key issue here is how to measure the sim ilarity between two different options.Note that according to the way of constructing options(Algorithm 4),an option can be illustrated asa chain of states linking one local subgoal to another.Therefore,the question essentially becomes how to measure the distance between two different chains of states.

We base our solution on the simple intuition that1)sim ilar chains should have similar lengths and 2)the states on two sim ilar chains should be correspondingly sim ilar.Note that such structuralmeasurementhasalready been used to describe the homomorphism between MDPs[15].One problem w ith homomorphism is that it requires strong conditions(in order to guarantee nice mathematical properties)and thus is not generally applicable[16].Recall thatourgoal is to reuseoptions to accelerate the learning.To this end,we believe that a weaker(i.e.,w ith lessmathematical properties)but generally applicablemeasurement ismore preferable.

LetM=〈S,A,T,R〉andM′=〈S′,A′,T′,R′〉be the source and target MDPs respectively.Letandbe two options constructed from the source and target MDPs respectively.Without loss of generality,let us assume thatIn addition,assume for themoment thatan injectivemappingffromI′toIisknown,ofwhich the functionality is to correlate sim ilar states.Wew ill explain the construction offshortly.Tomeasure the distancebetween two states,sands′,we use the follow ing formula w ith a positive(and typically small)thresholding parameterθ:

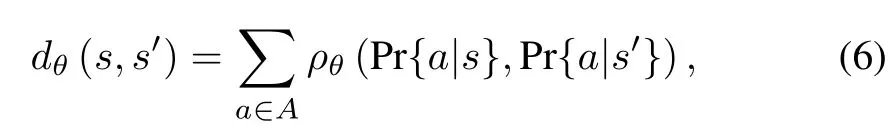
whereρθ(x,y)returns 0 ifand 1 otherw ise.The intuition behind(6)is that two states are sim ilar if the actions on them are sim ilar.ρθis in factused to penalize any dissimilarity.

Based on(6),the overall distance between two optionsoando′can thus be defined as

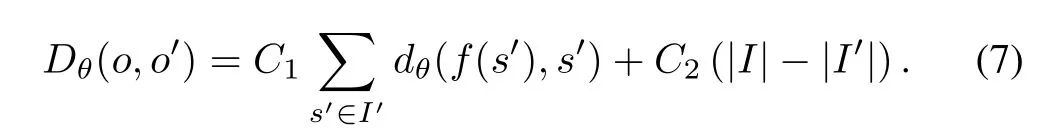
The two additive terms in(7)have clear meanings.As the mappingfmatches some states into pairs and leaves others(if any)unmatched,the fi rst term sumsup the distance between every matched states,while the second term penalizes the degree of non-matching.C1andC2are two positive constants controlling the relative importance of the corresponding factors.The distanceDθcan be easily transformed into a similarity measure as

We now explain how to obtain the mappingffromI′toI.First of all,given two MDPsM=〈S,A,T,R〉andM′=〈S′,A′,T′,R′〉,there aremethods to automatically find themapping.For example,Taylor etal.proposed a MASTER algorithm[13]to find onemapping betweenSandS′,another betweenAandA′.Their basic idea is to exam ine all the possible mappings and land on the ones w ith the m inimum error.Secondly,it is also possible to derive the mappingffrom a prioridomain know ledge.Forexample,inmazegames,it is natural to map a term ination state into a term ination state since usually the agent receives positives rewards after it accomplishes some goal(or subgoal).Themapping can then propagate reversely along the two option chains.Last but not least,themappingfcan also be determined manually,as is suggested by many researchers[17].

D.Reusing Options

Now given an optionoin the target taskM=〈S,A,T,R〉,we can find some sim ilar optiono′from some source taskM′=〈S′,A,T′,R′〉,

Note that(9)is merely another representation of the option〉wherefori=1,2,···,k−1,andβ′={sk}.In addition to the states and actions,there are in fact two more pieces of know ledge abouto′:(i),which can be estimated when taking sample episodes(Line 2 of Algorithm 3),and(ii)Q′(sk,a)for any valid actionain statesk,which is learnt already(Line 12 of A lgorithm 4).

The next step is to inject such know ledge ofo′into the learning ofM.The idea is straightforward,that wheneverois initiated we use thoseandQ′(sk,a)ofo′to updateQ(·,o)inM.To implement the idea,we augment the action setAto include options:an optionis valid in states∈Sifs∈I.After the augmentation,the learning agent choosesactionsasusual(using forexample the†-greedy policy[1]).If in statestthe agent chooses a prim itive actionat,thenQ(st,at)isupdated using(1)(direct learningw ithout transfer).If the chosen action isan optionot,and we can find a similar optiono′from the library,then we updateQ(st,ot)using the follow ing formula,

wherefis themapping discussed in Section II-B.Comparing to the rule of SMDP(3),(10)reuses past experience(rt′+i−1andQ′)to“skip”the learning ofot.

Algorithm 5 shows the pseudo-code for option transfer.Lines 6∼17 illustrate the transfer learning process.Note that before transfer learning,we preprocess the option setOto exclude those options for which we cannot find any suitable counterpart in the source library(Line 4).Such preprocessing is important due to two reasons.On one hand,it guarantees that during the transfer learning,whenever an option is initiated we can always find a reusable source option(Line 15).On the other hand,it reduces the risk of negative transfer.When a negative transfer happens,the learning agentw ill not beable to benefi t from the transfer.On the contrary,itw ill take the agent some extra effort to neutralize the effects.Finally,note that after the transfer learning process,a conventional learning method(such as Q-learning)is called to learn the optimal policy(Line 18).

A lgorithm 5.Transfer learning

Q=TRANSFERLEARNING(L,M,ψ)

Input.Lis the library of reusable options,M=〈S,A,T,R〉is the task to learn,ψis a positive threshold.

OutputQ-values ofMimplying the optimal policy

1)Apply A lgorithms 3 and 4 toMto get a setOof options

2)for each optiono∈Odo

3)SearchLfor the optiono′that ismost sim ilar too

4)if simθ(o,o′)＜ ψthen deleteofromO

5)AddOtoA,the action set ofM

6)for a small number of episodes do

7)s←s0▷s0is the initial state

8)whilesis not the term ination state do

9)Selecta∈A

10)ifais a primitive action then

11)Executea;observe the new states′

12)UpdateQ(s,a)using(1)

13)s←s′

14)else

15)Retrieve the optionothat is sim ilar toa

16)UpdateQ(s,a)using(10)

17)s←termination ofa

18)LearnMuntilQconverges

19)returnQ

E.Maintenance of the Source Library

So farwehaveexplained how to learn a target taskMfaster w ith the aid of a source libraryL.In practice,learning tasks come from time to time.A fter a target taskMis learnt,the learning experience(i.e.,options in our case)may be reused to speed up future tasks.Therefore from a systematic pointofview,the libraryLis evolving over time and requires some maintenance.

We have twomain concernsw ith respect to themaintenance ofL.One is the diversity of optionsand theother is the sizeof the library.Intuitively,on one hand,we expect the options in the library to be different from each other,so thatan incom ing option may have a higher chance to find somematch in the library.On the other hand,the library should be controlled w ithin a reasonable size,so that searching the library(Line 3 of Algorithm 5)w ill not become a bottleneck of the learning process.

A lgorithm 6 shows in detail how we maintain the library.As is indicated in Lines 2 and 3,we do not add every option into the library;the option to be included should be sufficiently different from the existing options in the library.Thisprinciple leadsalso to Lines5 and 6when the library becomes too large:one of the twomost sim ilar options shallbe expelled from the library.

A lgorithm 6.M aintenance of the library

MA INTA INLIBRARY(L,O,µ,κ)

Input.Lis the library of source options;Ois a set of new ly learnt options;µis a positive threshold;κis themaximum size of the library.

1)for each optiono∈Odo

2)if maxo′∈Lsimθ(o,o′)＜ µthen

3)Add optionointoL

4)while|L|＞κdo

5)(o1,o2)←argm axo,o′∈Lsimθ(o,o′)

6)Delete optiono1fromL

IV.EXPERIMENTS

In this section,we experimentally evaluate our proposed method.As a point of reference we also implemented Q-learning,Sarsa,and SDHRL[18](a subgoal-based learning method;w ill be briefly introduced in Section IV-B).We fi rst compare our method w ith the competitors to show the effectiveness of our method(Section IV-C).Then,we study the sensitivity of our method against varying parameters(Section IV-D).All algorithms have been implemented in C programm ing language.

A.The Grid World and Maze Games

We use thegrid world domain to examineourmethod.Over decades,such a domain has been extensively used by many researchers as a benchmark to test RL algorithms[14].Besides the popularity,we choose this domain also because it is easy to illustrate our idea.The subgoals and options we construct(Sections III-A and III-B)shall have clear physicalmeaning in such a domain,aswe w ill explain shortly.

As is shown in Fig.1,an instance of the grid world is a maze game where there is a rectangular area consisting of two different types of cells.White cells are accessible to the learning agent,whereas the black cells,which represent barriers,are inaccessible.Typically in eachmaze game,there isan initialposition and agoalposition.Forexample,in Fig.1,the initial position is at the upper left corner(marked w ith“S”)and the goal is,to the opposite,at the lower right corner(marked w ith“G”).

Fig.1. Two samplemaze games in the grid world domain.The left maze is simple,whereas the right one ismore complicated.

A learning agent in a maze game should learn to travel from the initial position to the goal position.The travel has a costwhich is in general proportional to length of the traveling trajectory.Therefore amaze game can bemodeled asan MDP w ithin which a learning agent w ill be motivated to find an optimal policy.In particular,the state spaceSis the set of allwhite cells.The action spaceAis the set of four possible actions up,down,left,and right.The transition probabilityTis set to be consistent w ith our intuition in general but w ith occasional disturbance.For example,when the agent at position“S”of Maze 1(Fig.2)takes the action down,then w ith probability 0.9 it w ill enter the cell right below“S”,butw ith the rest probability of 0.1 itw ill be transported to a random neighboring cell of“S”1Although itmight seem counter intuitive,the uncertainty here is in fact profound,in the sense that it compensates the somewhat optimistic reduction of any practical(complex)environment into an MDPmodel..Finally,the reward functionRis set to be

We fix the size of all the mazes to 21×21,thus there are roughly 400 states in amaze.

B.The Competitor Algorithms

To our best know ledge,there is no prior work that solves exactly the same problem as we do in this paper,we compare our proposedmethod w ithmost commonly-used existing methods.In particular,we compare ourmethod w ith two nontransfer learning methods,Q-learning and Sarsa,as well as one transfer learning method,SDHRL.

Non-transfer learning com petitors.We have introduced Q-learning and Sarsa as a piece of background know ledge in Section II-A.In our experiments,however,instead of the very basic versions introduced in Algorithms 1 and 2,we have actually implemented more advanced versions of these two algorithms,namely Q(λ)and Sarsa(λ).The advanced versions of these algorithms use eligibility traces to speed up the learning2The parameterλindicates the use of eligibility traces..An eligibility trace is a record of certain events,such as visiting states or taking actions.One example eligibility tracee(s,a)might look like the follow ing.

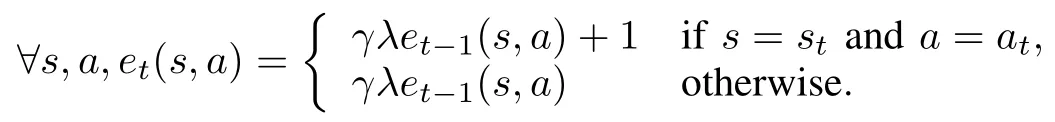
At every discrete time stept,the above eligibility trace reinforces(st,at),the state-action pair occurred att,whiledecaying(through a discount factorλ)all the other stateaction pairs.The idea of using eligibility traces is to reward notonly the immediate state-action pair(i.e.,(st,at))butalso the other state-action pairs thatever contributed to the learning episode.To avoid any distraction from ourmain focus in this paper,we om it the pseudocodes of Q(λ)and Sarsa(λ);they are,nonetheless,very similar to Algorithms 1 and 2,only w ith slightmodifications in their update rules.The parameterλtakes values from the range[0,1].Whenλ=0,Q(λ)and Sarsa(λ)degenerates to Q-learning and Sarsa,as introduced in Section II-A.

A transfer learning com petitor.In addition to the two conventional methods mentioned above,we also compare our algorithm w ith SDHRL[18],a well-known subgoal-based learning method.SDHRL works well in maze games w ith bottleneck states and it also discovers subgoals by searching a learned policy model for certain structural properties to accelerate learning in other tasks in which the same subgoals are useful.SDHRL uses Q-learning to learn themaze games for convergence,after the know ledge transfer.

There are several parameters in the above-mentioned learning algorithms.αis the learning rate andγdefines the discounting factor,both used in update rules such as(1)and(2).A lso,all the algorithms use the†-greedy policy(see Section II-A)to select actions,where†indicates the exploration probability.Without any specific clarification,in our experiments we setα=0.05,γ=0.9 and†=0.1 follow ing the suggestions of some early studies in RL[1].

C.Quality ofSubgoals and Options

The effectiveness of our transfer learning method relies greatly on the quality of subgoals and options.Hence we fi rstexam ine the effectiveness of the subgoal discovery(A lgorithm 3)and option construction(Algorithm 4).We carry out the experiment on Maze 1 of Fig.2 and Maze 2 of Fig.2.Parameters are set as follows:N=20,k=100,and†=0.1.

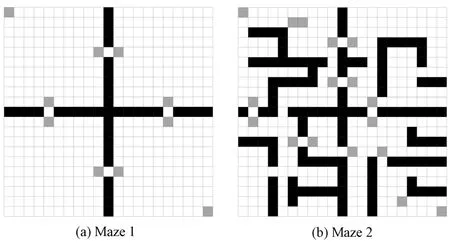
Fig.2. Local subgoals discovered in Maze 1 and Maze 2.

From Fig.2,we can observeseveral interesting facts.Firstly,we can see that our method effectively identifies all the key states in both mazes.A ll the local subgoals are around some gateways through the barrier.These gatewaysare indeed important states in the mazes,because in order to travel from one region to another across the barrier,such gateways must be accessed.Secondly,we see that,instead of gateways themselves,our method favors pairs of states which can be interpreted as the entrances and exits of the gateways.We believe that,comparing to individual subgoals being landmarks,such entrance-exit pairs provide better guidance to learning agents.Especially,recall that we construct options exactly based on pairsof local subgoals(Line 3 of Algorithm 4).Last but not least,ourmethod is robust against the variation of the environment.Themethod effectively identifies local subgoals in both simple and complex environments.

D.Effectiveness ofOur Proposed Method

We now compare ourmethod against Q(λ),Sarsa(λ),and SDHRL.The methodology is as follows.We fi rst random ly construct a series ofmazes w ith increasing complexity(controlled by the number and positions of black cells).Then,we process these mazes using our proposed algorithm,i.e.,we fi rst extract local subgoals,then construct the option library,and then learn thesemazes.The parameters used during this off-line preparation are listed in Table I.

TABLE I PARAMETER SETTINGS

After such an offl ine preparation,we learn(the simplest)Maze 1 and(themost complicated)Maze 2 online.We compare the online performance of our transfer learning algorithm(Algorithm 5)w ith the two non-transfer competitors,Q(λ)and Sarsa(λ),aswellas the transfer learning competitor,SDHRL.The parameterψat Line 4 of A lgorithm 5 is set to 0.9.That is,an option is transferred only if the similarity is larger than 0.9.We believe that this value prevents negative learning.We run each algorithm in each maze for 5 times.In each run,there are 2000 episodes.

Fig.3(a)and 3(b)show the comparison results on Maze 1 and Maze 2,respectively.Thex-axis represents the number of learning episodes(and thus the lapse of time).For a fixedx-value,the correspondingy-value represents theaverage cumulative return.

We see from the results that ourmethod outperform Q(λ),Sarsa(λ)and SDHRL in bothmazes.It converges very quickly in a few episodesand stick to the learntoptimal policy during the restof the learning process.It is clear thatboth ourmethod and SDHRL perform better than non-transfer methods Q(λ)and Sarsa(λ).In both mazes,Q(λ)needs more than 1000 episodes to convergewhereas this number for Sarsa(λ)is even more than 2000(i.e.,Sarsa(λ)fails to converge under our experiment setting of 2000 learning episodes).In contrast,transfer learningmethods(SDHRL and ours)converge to the optimal policy in merely a few dozens of episodes due to the transferred know ledge.Especially,ourmethod has the fastest convergence speed,which is several times faster than SDHRL and roughly two orders ofmagnitudes faster than those nontransfermethods.

E.Parameter Sensitivity Analysis

As has been stated above,all the algorithms studied in our experiments involve three learning parameters:1)the learningrateα,2)the exploitation probability†of the†-greedy policy,and 3)the eligibility trace decay factorλ.In all the experiments so far,we have set defaultα=0.05,†=0.1,and λ=0.Now we use the last set of experiments to show the sensitivity/stability of ourmethod,i.e.,the resistance against any variation of the above-mentioned learning parameters.We carry out a set of three experiments to test the sensitivity;in each experimentwe vary one of the three learning parameters and keep the other two fixed at their defaultvalues.We use the mostcomplexmaze,Maze2(Fig.2),forall theseexperiments.

Fig.3. Learning curvesw ith respect to Maze 1 and Maze 2.

In the fi rstexperiment,we varyαfrom 0.05 to 0.2w ith step size 0.01,while keeping†andλat their default values,0.1 and 0,respectively.Fig.4 shows the resultof this experiment.

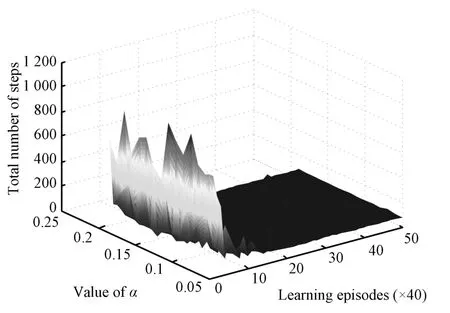
Fig.4. Learning curves of ourmethod w ith different learning rates.

The x-axis(“Learning episodes”)represents the number of learning episodes and thus the lapse of time.The y-axis(“Value ofα”)represents the variation of the value ofα.The z-axis(“Total number of steps”)shows the total number of steps theagent takes form thestarting state“S”to thegoalstate“G”.For a specific(x,y,z),itmeans thatunder the parameter settingα=y,the agent takes z steps to arrive at the goal state during the x-th learning episode.Aswe can see,whenα changes,there is no significantdifference between the curves.A fter an initial vibration,all the curves rapidly converge to the optimal value.

The nextexperiment is conducted to test the stability of our method against†,the exploration probability in the†-greedy action selection policy.In this experiment,we fixαandλat 0.05 and 0 respectively,and vary†from 0.1 to 0.3 w ith step size 0.01.Fig.5 shows the result,which is very sim ilar to the resultof Fig.5.In all cases,the learning curves converge very quickly.

Fig.5. Learning curves of ourmethod w ith different†.

The last experiment is conducted to test the stability of our method againstλ.In this experiment,we fixαand†at 0.05 and 0.1 respectively,and setλas 0.1 and 0.3.The results are shown in Fig.6(a)(λ=0.1)and Fig.6(b)(λ=0.3)respectively.In both cases,our method outperforms Q(λ),Sarsa(λ),and SDHRL.

These resultsare very similar to thoseof Fig.3(a)and 3(b).As in Fig.3(a)and 3(b),the convergence of Sarsa(λ)is slow here for eitherλ=0.1 orλ=0.3.It is clear that the relative performance aswell as the converging trends in Fig.6(a)and 6(b)(and also Fig.3(a)and 3(b))are basically the same.Note that the decay factorλor the eligibility trace mechanism is designed to improve the performance of basic RL algorithms such as Q-learning and Sarsa,thus the stability of ourmethod againstλindicates that ourmethod is constantly better than thosemethods that rely on the eligibility tracemechanism.

Fig.6. Learning curves w ith respect to Maze 1 and Maze 2.

V.RELATEDWORK

McGovern et al.[4]usemultiple-instance learning(MIL)to find the subgoals and transfer their policies to target task to speed up the learning.The determ ination of the subgoals depends on the occurring frequencies of states in learning episodes.In particular,they consider both successful and unsuccessful learning trajectories.The subgoals are those states w ith the highest frequencies.However,aswe have argued in Section III-A,the subgoalswe really need are thosebottleneck states which can be helpful in finding successful trajectory.

Lazaric etal.[3]selectamost sim ilar task from source tasks and transfer the policies to the target task to speed up the learning.By using the sim ilarity between tasks,their algorithm chooses amost sim ilar task from a learnt source tasks library,and then transfers the policy of the selected task to the target task.Our proposed method differs from theirmethod,in that we are able to take advantage of multiple source tasks.We argue that two ormore source tasksm ight be equally useful to a target task,and thus it is reasonable to consider notonly the most sim ilar task but also all the source tasks that are similar enough to the target task.

Ferns et al.[19]study the similarity measure between states in one MDP.The measure is built upon the Kantorovich distance(a.k.a earth movers distance,EMD)between the two transition probability distributions of two states in the same MDP.However,their distancemeasure is not desirable in our problem setting because of the follow ing reasons.First of all,their distancemeasure requires complete know ledge about the environment(so that the distance can be calculated).This is impossible in our problem setting that the learning agent has no a priori know ledge about the incom ing tasks.Second,their distancemeasure is only applicable to two states in the same MDP.This is because,for Kantorovich distance tomake sense,the two probability distributions of which the distance is to be calculated must be defined upon the same set of“bins”(i.e.,mustbe defined upon the same domain).However,in our problem setting,we allow different state spaces in different tasks,therefore there is no common domain for different transition probability distributions in different tasks.Lastbutnot least,itiswell-known thatcomputing Kantorovich distance is time-consum ing.Sometimes it is even slower than learning from scratch,and therefore it cannot guarantee the acceleration of learning.

Mehtaetal.[20]study transfer learning under theassumption that the tasks are identical except for the reward function.In theirwork,they view a reward function asa linear combination of rewarding features.They use hierarchical RL method to divide a task into subtasks,and then transfer know ledge between subtasks.Although the method is cheap in terms of time cost,in order for it to be applicable the task must have hierarchical structures.Moreover,the division of the hierarchical structure and the selection of the reward features much be known in advance and manually done.

V I.CONCLUSION

In this paper,we study the problem of reinforcement learning transfer from a library of source tasks(to be precise,a library of reusable units).That being the purpose,we present a novel concept called local subgoals.We identify the local subgoalsw ith two conditions.Using the local subgoals instead of the global ones,we are able to build a library of reusable options,which can aid the learning of new tasks.Upon learning a new task,we fi rst find,w ithin the source library,all the reusable options that are potentially useful for this task,during which process the key is our proposed novel sim ilarity measurebetween options.We carry outextensiveexperimental studies,ofwhich the resultsshow thatourmethod significantly outperforms the state-of-the-artmethods.

In the future,we shall tackle more challenge tasks.For example,instead of the maze games in the grid world,we would like to study RL and transfer learning in practical domains such as computer video games.We would also like to consider other(and possibly better)sim ilarity measures between options and MDPs.Last but not least,we are interested in maintaining the source task library from the data engineering perspective;we w ish to efficiently maintain the library for a large amount of source tasks.

[1]Sutton R S,Barto A G.Reinforcement Learning:An Introduction.Cambridge,MA:The M IT Press,1998.

[2]Fern´andez F,Garc´ıa J,Veloso M.Probabilistic policy reuse for intertask transfer learning.Roboticsand Autonomous Systems,2010,58(7):866−871

[3]Lazaric A,Restelli M,Bonarini A.Transfer of samples in batch reinforcement learning.In:Proceedings of the 25th Annual International Conference on Machine Learning.New York,NY:ACM,2008.544−551

[4]M cGovern A,Barto A G.Automatic discovery of subgoals in reinforcement learning using diverse density.In:Proceedings of the 18th International Conference on Machine Learning.San Francisco,CA,USA:Morgan Kaufmann Publishers,2001.361−368

[5]Pan S J,Tsang IW,Kwok J T,Yang Q.Domain adaptation via transfer component analysis.IEEE Transactions on Neural Networks,2011,22(2):199−210

[6]Taylor M E,Stone P.An introduction to intertask transfer for reinforcement learning.AIMagazine,2011,32(1):15−34

[7]Zhu Mei-Qiang,Cheng Yu-Hu,LiM ing,Wang Xue-Song,Feng Huan-Ting.A hybrid transfer algorithm for reinforcement learning based on spectralmethod.Acta Automatica Sinica,2012,38(11):1765−1776(in Chinese)

[8]Watkins C,Dayan P.Q-learning.Machine Learning,1992,8(3):279−292

[9]Rummery G A,Niranjan M.On-line Q-learning using Connectionist Systems,Technical Report CUED/F-INFENG/TR 166,Department of Engineering,Cambridge University,Cambridge,UK,1994.

[10]Sutton R S,Precup D,Singh S.Between MDPs and semi-MDPs:a framework for temporal abstraction in reinforcement learning.Artificial Intelligence,1999,112(1):181−211

[11]Stolle M,Precup D.Learning options in reinforcement learning.In:Proceedings of the 5th International Symposium on Abstraction,Reformulation and Approximation.Kananaskis,A lberta,Canada:Springer,2002.212−223

[12]¨Ozgur¨u S,Alicia PW,Andrew G B.Identifying useful subgoals in reinforcement learning by localgraph partitioning.In:Proceeding of the 22nd International Conference on Machine Learning.Bonn,Germany:ACM,2005.816−823

[13]Taylor M E,Kuhlmann G,Stone P.Autonomous transfer for reinforcement learning.In:Proceedingsof the 7th International Joint Conference on Autonomous Agents and Multiagent Systems.Estoril,Portugal:ACM,2008.283−290

[14]Chen F,Gao F,Chen S F,Ma Z D.Connect-based subgoal discovery for options in hierarchical reinforcement learning.In:Proceedings of the 3rd International Conference on Natural Computation(ICNC′02).Haikou,China:IEEE,2007.698−702

[15]Ravindran B,Barto A G.An A lgebraic Approach to Abstraction in Reinforcement Learning[Ph.D.dissertation],University of Massachusetts Amherst,USA,2004

[16]Soni V,Singh S.Using homomorphisms to transfer options across continuous reinforcement learning domains.In:Proceedings of the 21st International Conference on Artificial Intelligence(AAAI′06).Boston,Massachusetts:AAAIPress,2006.494−499

[17]Wolfe A P,Barto A G,Andrew G.Decision tree methods for finding reusable MDP homomorphism.In:Proceedings of the 21st International Conference on Artifi cial Intelligence(AAAI′06).Boston,Massachusetts:AAAIPress,2006.530−535

[18]Goel S,Huber M.Subgoal discovery for hierachical reinforcement learning using learned policies.In:Proceedingsof the 16th International FLAIRSConference.California,USA:AAAI,2003.346−350

[19]Ferns N,Panangaden P,Precup D.Metrics for finite Markov decision processes.In:Proceeding of the 20th Conference on Uncertainty in Artifi cial Intelligence.Banff,Canada:AUAIPress,2004.162−169

[20]Mehta N,Natarajan S,Tadepalli P,Fern A.Transfer in variable-reward hierarchical reinforcement learning.Machine Learning,2008,73(3):289−312