Clique-based Cooperative Multiagent Reinforcement Learning Using Factor Graphs

Zhen Zhang Dongbin Zhao

I.INTRODUCTION

T HE conceptof agentplaysan important role in the design of artif cial intelligence.An agent can be viewed as a computationalentity thatcan perceive itsenvironment through sensors,make decisions according to a prior know ledge and sensed information,and act upon its environment through actuators[1].The design goal of agent is to optim ize some performance index.For example,a traff c signal light agent determ ines its phase and cycle time according to the traff c information transm itted from the sensors of nearby lanes[2],w ith the aim ofm inim izing the averagewaiting time orqueues of the vehicles crossing the intersection[3]or entering the freeway ramps[4].In many cases,an agent is not standalone but connected w ith others,and agents interactw ith each other to affect the environment together.Sometimes,each agent can only acquire the states of its nearby environment and the behaviors of its neighbor agents.Such a system is called multiagent system(MAS)[5].If agents have common interest and coordinate to fulf lla task,they are cooperativeones,e.g.,w ireless network agents cooperate to formulate a stable grand coalition formation to yield signif cant gains w ith respect to average ratesper link[6].Otherw ise,if each agentonly pursues the interest of its own,they are competitive ones,e.g.,the agents in one-on-one combatgames competew ith each other to make the maximum prof t of each individual[7−8].In this paper,we only dealw ith cooperativeagents.In MAS,an agent has to learn its strategy from the environmentand the others.This makes the learning system more unstable to converge.Thus,an important problem in MAS is how to make agents achieve cooperation w ith partial state information and the behaviors of their neighbors[9−10].

The strategiesof the agents can be programmed in advance,if there is suff cient a priori know ledge about the problem.However,in many cases,the environmentmay change over time,which makes the hardw ired strategies hardly fexible.Thus it isnecessary foragents to learn strategieson theirown.

Reinforcement learning(RL)[11]is a naturalway to design adaptiveagents.Unlikesupervised learning,RL learnsby trialand-errorw ithoutan explicit teacher.This isvery important for designing agent,especially in case where a priori know ledge is limited.A strategy learned by RL is represented by a value function or a Q-value function.A value function maps each state to some value as an estimation of the state′s goodness in the long run,while a Q-value functionmaps each state-action pair to some value as an estimation of the action′s goodness in the long run.When RL is employed,a transition function can be estimated and used to update the value function online.Previous studies have shown that this can reduce the learning time greatly[12].

The learning dynamics or convergence ofmultiagent reinforcement learning(MARL)is the theoretical foundation.The early analysison the dynam icsof RL in cooperativeMASwas done by Claus and Boutilier[13].They analyzed the dynam ics of independent learnersin a two-agent repeated game.Besides,Tuyls[14]analyzed independentQ-learning(IQL)through evolutionary game theory.Gomes and Kowalczyk[15]analyzed IQL w ithε-greedy exploration.Kianercy and Galstyan[16]analyzed IQL w ith Boltzmann exploration.These results have given inspiration for designing MARL algorithms.In fact,most theoretical results on MARL are lim ited to repeated games.Drawn from Markov decision processand game theory,stochastic games are proposed as a general framework for studying MARL[17−18].Under this framework,many MARL algorithms have been presented.Examples arem inimax-Q[17],Friend-or-foe[19],Nash-Q[20],IGA[21],and Wolf-PHC[22].As the number of agents increases,the state space and the joint action space grow rapidly,which is the so-called problem of curse of dimensionality in MARL.Researchershavemanaged to suggest many algorithms and studied them in different domains.Adaptive dynam ic programm ing(ADP)[23−29]is an effective approach to relieve such problem by using neural networks to approximate the value function and the policy.ADP has been applied to many felds such as air-fuel ratiocontrol[30],adaptive cruise control[31]and pendulum robots control[32].Crites and Barto[33]used the global reward Q-learning to dispatch a group of elevators.Bazzan etal.[34−35]split traff c signal light agents into groups to reduce the joint action space and proposed a way of coordinating many agents in stochastic games.Kok et al.[36]proposed sparse cooperative Q-learning,where the global Q-value function was decomposed into local Q-value functions,each of which depended only on a small subset of all variables of state and action.Each agentmaintained a local Q-value function and updated it w ith the greedy joint action which was obtained by the max-plus algorithm[37].However,two problems still remain to be adequately addressed.First,the original sparse Q-learning isnotusedw ith a transition function,which usually means a relatively low learning speed.Second,themax-plus algorithm can only dealw ith localQ-value functionsw ith two variables,which lim its the generalization of global function decomposition.

In this paper,our aim is to solve the coordination problem for a class of multiagent systems on tasks which can be decomposed into subtasks.We dealw ith the problem in two aspects.First,a transition function is estimated and used to update the Q-value function w ith the aim of reducing the learning time.Second,it ismore reasonable to divide agents into cliques,each ofwhich is responsible fora specif c subtask.In this case,the global Q-value function is decomposed into the sum of several simpler local Q-value functions which can contain more than two variables.This implies thatmore fexible decomposition can be considered according to the problem.Such decomposition can be expressed by a factor graph and exploited by the generalmax-plus algorithm to get the greedy joint action in a distributed manner.

Thispaper isorganized as follows.In Section II,we describe the problem of the coordination for a distributed sensor network(DSN).Section III introduces stochastic games and gives possible popular MARL algorithms for comparison.In Section IV,the clique-based sparse cooperative RL algorithm using factor graphs is proposed.We w ill show how to update the transition function,how to decompose agents into cliques,and how to use a factor graph to solve the problem.In Section V,the experimental results of various MARL algorithms are presented and compared.Section VIgives the conclusions.

II.DISTRIBUTED SENSOR NETWORKS

The DSN problem is a distributed optim ization problem whichwaspartof the NIPS 2005 benchmarkingworkshop[38].It is composed of two arrays of sensors.Fig.1 shows a DSN w ith eight sensors,each of which has three actions,i.e.,focusing on its left,focusing on its rightornot focusing atall.Notice that the action range of corner sensors is not limited to cells.For example,Sensor 0 can focus on its left even if that focus is outside of any cell.There are two targetsmoving w ithin three cells.Each target has equal probability to move to its left cell,move to its right cell or just stay where it is.The two targets take actions according to the order from left to right.Each cell can be occupied by atmost one target at one time.If a targetdecides tomove outside of the three cells ormove to a cellwhich has already been occupied by another target,itw ill stay where it is.Each target has themaximum energy value(i.e.,3)in the beginning.The energy of a target w ill be decreased by 1 which is called a hit,if at least three sensors focus on the cell it stays in.If its energy value is 0 which is called a capture,itw ill get vanished from DSN and do not occupy any cell at all.If all targets are elim inated or 300 steps elapse,an episode is fnished[39].

The credit assignment setting follows[39].Every focus action produces a reward of−1.No focus produces a reward of 0.If a capture is caused by four sensors,only the sensors w ith three highest indices are rewarded by 10,respectively.

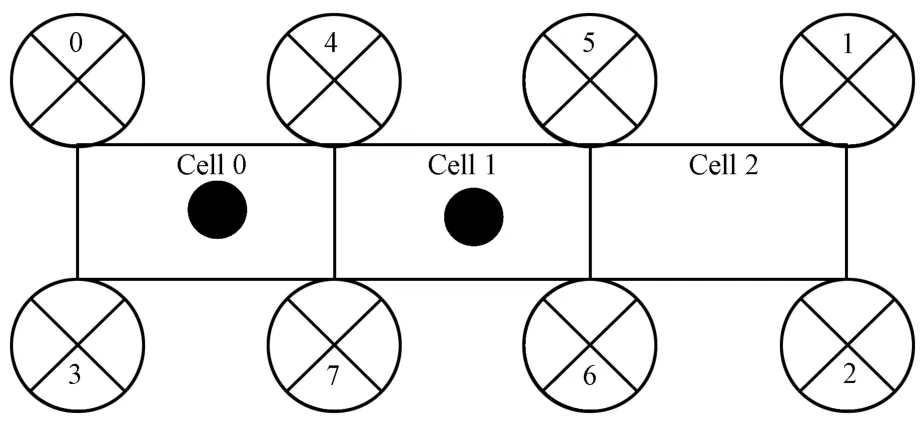
Fig.1. A distributed sensor network w ith eight sensors⊗and two targets•.

Notice that sensors do not know whether a hit or a capture hashappened but they know theactionsof theirneighbors.The aim is to obtain asmany accumulated rewardsaspossible in an episode.In this paper,two targets are initially located in two random cells.During each step,the sensors make decisions and act on targets f rst,causing an intermediate state,then it is the turn for targets to move,transferring to the next state.It is clear that the immediate reward is only dependenton the intermediate state,for they contain the information ofwhether there is a hit,a capture,focus or no focus.Moreover,we assume that intermediate states can be sensed by all sensors.

In this problem,there are totally 38=6561 actions and 37 states.In theory,the single agent RL algorithm can learn the optimal strategies for a group of agents if they are regarded as awhole.Nevertheless,there are two issues thatmake it infeasible for the DSN problem.First,the jointaction space grows exponentially as the number of agents increases.Exploring so many state action pairs would be arduous.Second,in the DSN problem,it is impossible for each agent to observe the complete environment state and the actions taken by all the other agents.Next,we introduce severalMARL algorithms to solve these problems to some extent.

III.COOPERATIVEMULTIAGENT RL

In cooperative MAS,all agents act together to make their environment transit from one state to another,and then they get an immediate global reward.Their objective is to get the maximum accumulated global reward in the long run.Next,we w ill introduce the theoretical framework that represents such a problem,i.e.,stochastic games.Then,several popular MARL algorithmsw ill be introduced and compared w ith the proposed algorithm.

A.StochasticGames

A stochastic game[17]is a tuple＜S,p,A1,A2,···,An,r1,r2,···,rn＞,where S is a fnite or infnite set of environment states,n is the number of agents,Aiis the set of agent i′s actions for i=1,2,···,n,the transition functionp:S×A1×A2×···×An×S→[0,1]determines the probability of transition from state sss to sss′under the jointaction aaa of all agents,and ri:S×A1×A2×···×An×S′→R is the immediate local reward function ofagent i.The immediate global reward of all agents isWe defne A=A1×A2×···×Anas the setof aaa,aias agent i′saction and aaaias the jointaction ofagent i and itsneighbors.The learning objective is to maxim ize the cumulative global reward at each time t,i.e.,

whereγis the discount factor w ithin[0,1],T is the ending time of an episode,and r(t+1)is the immediate global reward actually received at time t+1.The smallerγis,the more important the rewards at early times become.

A Q-value function represents the expected cumulative global reward for a state sss when selecting an action aaa.According to the Bellman equation,the optimalQ-value function can be obtained by

Once the optimal Q-value function is computed,the greedy joint action for state sss is maxaaaQ∗(sss,aaa).For completeness,we give the single agent RL algorithm f rst.

B.SingleAgentRL

We implement single agent RL using value iteration scheme[11],which is a standard way of solving dynam ic programm ing problems.In fact,it is an iterative form of Bellman equation.In value iteration,a transition function is estimated and used to update the Q-value function online as

The jointaction aaa isselected by the follow ingε-greedy policy:

whereε∈(0,1)is the exploration rate.Next,we introduce severalMARL algorithms,whereε-greedymethod isalso used to balance exploitation and exploration.

C.IndependentRL

In independent RL[40],each agent stores and updates a Q-value function of its own.For agent i,the updating rule is

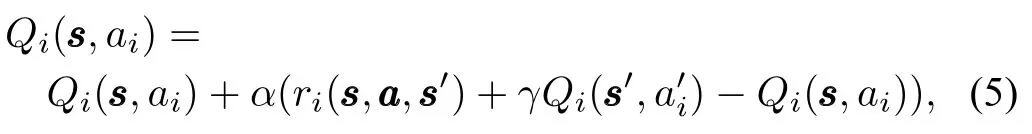
whereα∈(0,1)is the learning rate that controls theweights of the old Q-value and the estimated error.The dynam ics of independent RL have been extensively studied in repeated games[14−16].Although there isno guarantee for convergence,this algorithm has been applied in some situations.

D.MultiagentQ-learningwithJoinStateValueApproximation

Themotivation of themultiagentQ-learning w ith jointstate value approximation(MQVA)[41]is to relieve the dimension disasterproblem.Twomain processesaredescribed as follows.First,each agent stores a Q-value function and updates it according to

Second,the joint state value function V(sss)is updated as

E.SparseRL

Sparse RL[36]is based on the assumption that the global Q-value function can be decomposed into local Q-value functions,each of which is dependent on actions of fewer agents.The dependency between agents can be visualised by a coordinated graph(CG)[42].A CG is a bipartite graph G=(V,E),in which each node∈V represents an agentand each edge(i,j)∈E meansagents i and j areneighbors.Once the structure of a CG is settled,itw ill not change thereafter.The global function can be decomposed in terms of agents or edges.In this subsection,we only introduce agent-based sparse RL and edge based sparse RL w ith edge updating.

1)Agent-basedsparseRL:The global function can be decomposed in terms of agents.Each agent stores a local Q-value function that depends on a small subset of variables of all state and action.Each agent i updates its Q-value function by

where sssiis the state which can be perceived by agent i.Here,we defne the global Q-value function as,the greedy joint action as aaa=argmaxaaaQ(sss,aaa),and the joint action of agent i and its neighborsas aaai.We can see that themajor difference between sparse RL and other MARL algorithms is that it updates local functions using greedy joint actions instead of local greedy actionsw ith the aim of achievingmaximum globalQ-value at any time[36].

2)Edge-basedsparseRL:Another method of decomposition is based on edges.The global function is decomposed into local functions,each ofwhich dependson the jointaction of two agents connected by an edge.Its advantage lies in that the computation expenseofglobal function grows linearlyw ith the number of neighbors.One way to assign credit between edges is the edge-updating rule[36],i.e.,

where is the number of agent i′s neighbors,sssijis the state perceived by agent i and j.Themax-plus algorithm is used to derive the greedy joint action[37].

IV.CLIQUE-BASED SPARSE RL USING FACTOR GRAPHS

So far,we have reviewed severalMARL algorithms.Among them,the sparse RL algorithm has a great potential to learn the optimal global Q-value function and the optimal policy in a distributed way.Its advantage over others is that it utilizes the dependency between agents to decompose the global Q-value function.Then the greedy joint action is computed and evaluated in a distributed way while others just evaluate local greedy actions.However,two problems still remain to be adequately addressed.First,the convergence speed of the original sparse RL is slow.Second,the global function can only be decomposed into local functions containing two variables,which might be unreasonable in some cases.Thus in the next section we extend it to the case that local functions contain more than two arguments.We w ill show that the proposed method reduces the learning time and improves the quality of learned strategies.

A.SparseRLwithaTransitionFunction

We combine the original sparse RL[36]w ith a transition function to update the Q-value function as The transition function p is updated online by counting method[11].The pseudo-code of the complete algorithm for agent i isgiven in A lgorithm 1.represents thenumber of visited state-action pairrepresents the number of visited state-action-state triple

Algorithm 1.The pseudo-code of model-based sparse RL algorithm.

The greedy joint action aaa is acquired by the generalmaxplusalgorithm whichw illbe described later.Notice thatwhen a local function is being updated,it is impossible for agent i to independently acquire the greedy joint action in each statethe only thing it can do is to resort to a table memory actionin which once stateismet,the computed greedy joint actionis stored.

In the DSN problem,the immediate local reward and the next state are determined after the actions are performed.Equation(10)can be simplifed as

Thus only the transition function p:needs to be estimated.

B.Clique-basedDecomposition

How to assign creditsamongmultipleagentsisan important issue in MAS.The simplest approach is to split the global reward equally among agents.This method is called global reward and is w idely used in cooperative MAS.It may produce lazy agents because the reward received by an agent does not necessarily depend on its own contribution.Another extreme way is to assign credits to each agent according to its own behavior,which is called local reward.But its fnal outcome may deviate from the designer′s original intention,i.e.,cooperation,for there isno explicitmechanism to promote agents to help each other[43].

In this paper,we propose a new method by hybridizing the twomethodsmentioned above.In fact,ourmethod is very sim ilar to hybrid team learning[43]which hasbeen investigated in genetic programm ing by Luke[44].In this kind of learning,agents w ith the same local interest are clustered into one clique.In each clique,there isone learner in chargeof learning and deciding foreach agentw ithin the same clique.It receives rewards according to the performance of its clique,stores and updates a local Q-value function which is dependent on the local states sensed by its clique and the jointactionsof agents in its clique.

As shown in Fig.2,eightsensorsare split into three cliques.We cluster them in the way that each clique is responsible for hitting and capturing a target in a cell.The topology is stationary thereafter.

Since there are overlaps between cliques,we make the follow ing creditassignment rules.Each clique occupiesa cell,forexample,Clique0 occupiesCell0.In each step,if a sensor doesnot focuson the celloccupied by its clique,its immediate reward w ill not be added into its clique.Each clique can only sensewhathappened in the cell itoccupies.Take Clique 1 for example,it can only distinguish four states,i.e.,whether there is a target in Cell 1,and how much energy is left(1,2,or 3).

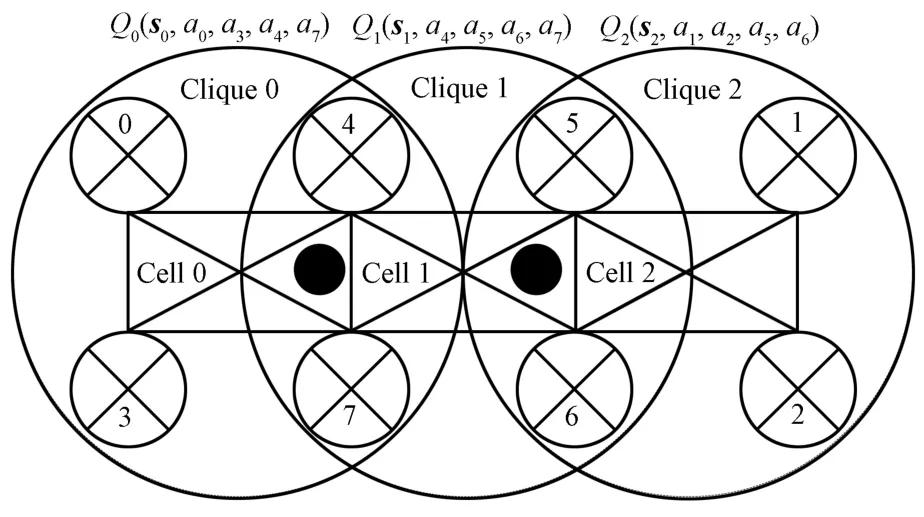
Fig.2. Clique-based decomposition.

C.Factor Graphs and The GeneralMax-plus Algorithm

The suggestion to use factorgraphscomes from[39].As for a specif c state,Q-value function is only dependenton action variables.Thus the global Q-value function is decomposed in terms of cliques as

where the local Q-value functions Q0,Q1,and Q2are stored and updated by the learners of the three cliques,respectively.Decomposition(12)can be expressed by a factor graph[45]as shown in Fig.3(a).A factor graph is a bipartite graph,and it comprises variable nodesand factor nodes.A variable node is visualized as an empty circle to representa variable.A factor node is visualized as a solid square to represent a factor.For clarity,we use node(ai)and node(Qj)to represent the node for variable aiand the node for function Qj,respectively.An edge connects node(ai)and node(Qj)if and only if aiis an argumentof Qj.Two nodes are neighbors if and only if there is an edge between them.The decomposition of the globalQ-value function in the DSN problem should obey the follow ing rules.On one hand,the factor graph of the sum of the local Q-value functions should be connected,that is,there should be at least one path for any two nodes in the factor graph.

Otherw ise,theremustbe standalone agentsor cliques.On the other hand,the loops in the factor graph should be as few as possible,because they w ill cause explosion of messages during themessage passing process.Eff cient algorithms for solving themaximum of(12)often exploit the possibility of factorizing the global function.The f rst such algorithm is belief propagation[46]which is used to approximatemarginal probability in a Bayesian belief network.Kschischang etal.[45]proposed a generalmanner of belief propagation in a factor graph which is called sum-product algorithm.The general max-plus algorithm can be obtained from the sum-product algorithm once we use maxim ization instead of summation and then transform it to log domain.It follows a simple rule thateach node keeps sendingmessages to all of its neighbors until the term ination condition ismet.There are two types of messages.Let N(x)represent the set of neighbors of node x.Themessage sent from the variable node node(ai)to the factor node node(Qj)is

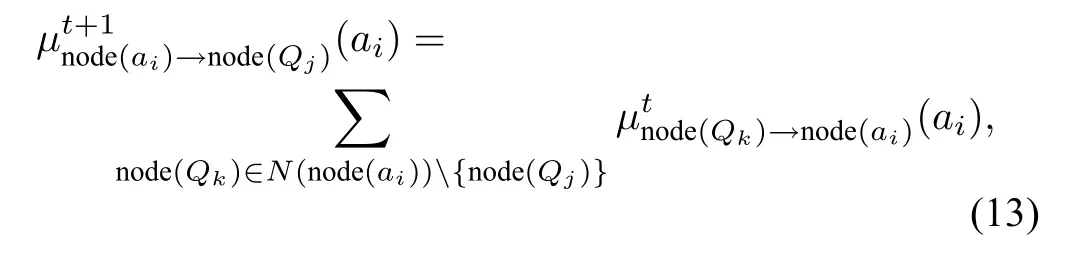
where N(node(ai)){node(Qj)}denotes the set of nodes which belong to N(node(ai))except node(Qj).

Themessageµsent from the factor node node(Qp)to the variable node node(al)is

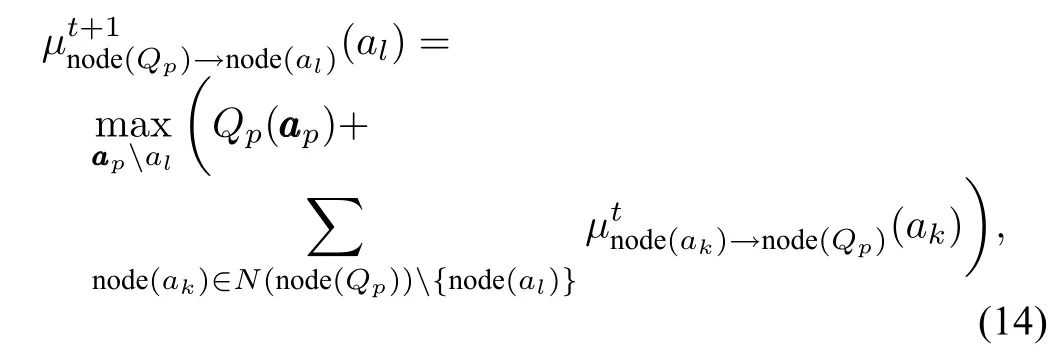
where aaapalrepresents the arguments of local function Qpexcept al.Whenmessagesdo notchangeany longeror the predefned numberof iterations is reached,themaximum solution can be computed by maxim izing messages received by each variable node,respectively,as

The pseudo-code of the general max-plus algorithm is shown in A lgorithm 2.The number of variable nodes and factor nodes are represented by n and m,respectively.In a factor graph,message sending can be sequential or parallel.In one way,messages are sent step by step from leaf nodes to root nodes and then back propagated from root nodes to leaf nodes.In another way,as shown in Algorithm 2,one node does not have to wait for incom ing messages before sending them.If a unique aiexists formaximizing b(ai),the maximum solution is unique[47].Under this assumption,exact solution could be obtained by using the general max-plus algorithm in a loop-free factor graph.

Algorithm 2.The pseudo-code of the generalmax-p lus algorithm

1:Initialize

N(node(ai)),i=1,2,···,n

N(node(Qp)),p=1,2,···,m

4:Time t=0

5:repeat

6:for each variable node node(ai)do

7:for each factor node node(Qj)∈N(node(ai))do

8:Send message for all ai∈Ai

10:end for

11:end for

12:for each factor node node(Qp)do

13:for each variable node nodedo

14:Send message for all al∈Al

16:end for

17:end for

18:t=t+1

19:until specifed iteration number is reached

20:for each variable node node(ai)do

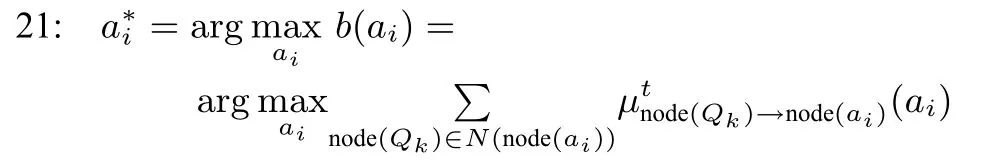
22:end for

23:return

As shown in Fig.3(a),the factor graph contains loops.Under these circumstances,the exactsolution cannotbe guaranteed by using the generalmax-plus algorithm directly.This is due to the fact that themessages received by a node contain themessage sent right from it in an undeterm inedway,leading to an explosion ofmessages.Thisproblem can bealleviated by using asynchronousmessage passing[48]and message passing w ith damping[49].Themechanism ofmessage passing is still unclear,nevertheless,the belief propagation like algorithms have shown greatsuccess in some situations,for example,the decoding of turbo codes[50].

Here,to get the exact maximum of(12),we break the loops by merging variable nodes node(a5),node(a6)into one node and node(a4),node(a7)into another node,as shown in Fig.3(b).The domain of the emerged variables is A56=A5×A6and A47=A4×A7.

Q0(a0,a3,a4,a7)+Q1(a4,a5,a6,a7)+Q2(a1,a2,a5,a6)

Fig.3. The factor graph for clique-based decomposition.

In clique-based decomposition,there m ight be more than two agents in a clique,whichmeans a local Q-value function may havemore than two action variables.In this situation,the maxim ization problem cannotbe tackled directly by using the max-plus algorithm proposed by Kok etal.[37].A lthough their techniques can be generalized to local functions w ith more than two variables by converting the concerned graph to one w ith only pairw ise inter-agent dependencies,we believe that it ismore naturaland convenient to use factor graphs and the generalmax-plus algorithm to get the greedy jointaction in a distributed manner.

Next,we w ill test our proposed algorithm as well as the reviewed MARL algorithms on a stochastic game-distributed sensor network.

V.EXPERIMENTS

In this section,a DSN w ith eight sensors and two targets shown in Fig.1 is used as our test-bed for the proposed algorithm and other MARL algorithms.

A.Experiment Settings

We average the resultsof 50 runs,each ofwhich comprises nl=10000 learning episodes and 5000 strategy evaluation episodes.In each learning episode,Q-value functions are updated online and actions are selected w ithε-greedy policy.Exploration is performed synchronously,which means all learnersexploreorexploitateach step.To realizesynchronization,we set the same random seed foreach sensorand activate them simultaneously.In each strategy evaluation episode,Q-value functions are stationary and the greedy joint action is always selected.We only present the average performance of 50 episodes which is an episode block.During learning,the learning rate is decreased linearly w ith the numberof learning episodes as

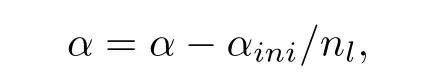
whereαiniis the initial learning rate and is set to be 0.7.The exploration rateεis constantand isset to be0.2.The discount factorγis constant and is set to be 0.9.As for the general max-plus algorithm,themaximal iteration number is set to be 10.

For a DSN problem,global states mean the position and energy of all targets.Local states are referred to the local environment states which can be sensed by a clique.For example,the learning agent for Clique 1 can sense and distinguish four different local states,i.e.,whether there is a target in Cell 0 and how much energy is left(1,2,or 3).Agent-based sparse RL,edge-based sparse RL,and the proposed algorithm clique-based sparse RL w ith a transition function employ only local state information while the others use global states information.

B.Experiment Results

We list the experimental results of single agent RL and MARL algorithms in Fig.4 for clear comparison.

Single agent RL shows good performance in both average accumulated rewardsand steps.However,itobtains thegreedy joint action by exhaustion,which means,if there are more sensors in the network,itwould probably fail to learn a good strategy in time.

Independent RL takesmuch more steps to capture targets compared to the other algorithms,so its performance is not shown in Fig.4(d).We analyze its learnt strategy and fnd out that sensors do not focus on some states at all.Thisw ill not infuence the accumulated rewardsbutdo increase the number of steps to capture targets.IndependentRL and MQVA obtain less rewards than theotheralgorithms.Wenote that thegreedy joint action of either independent RL or MQVA is composed of each agent′s greedy action.A lthough MQVA uses the joint state value function to update each agent′s Q-value function,it does not concern other agents′infuence.Since each agent only takes care of itself,it is hard for them to cooperate well.MQVA and edge-based sparse RL take thesecond largest number of steps to capture targets.

Agent-based sparse RL shows an average performance.It is a naturalway to decompose a task in terms of agents.Yet,it is better to split them into several different cliques in the DSN problem.The average accumulated rewards obtained in this paper are higher than those obtained in[39].The reason mightbe the higher learning rate adopted in this paper.

The proposed clique-based sparse RL w ith a transition function gains the highest average accumulated rewards in m inimal steps among all algorithms,that is,more than 41 average accumulated rewards in slightly more than 3 steps,which is close to the best possible performance,i.e.,42 rewards in 3 steps[39].Moreover,it learns faster than any other algorithm,as shown in Fig.4.

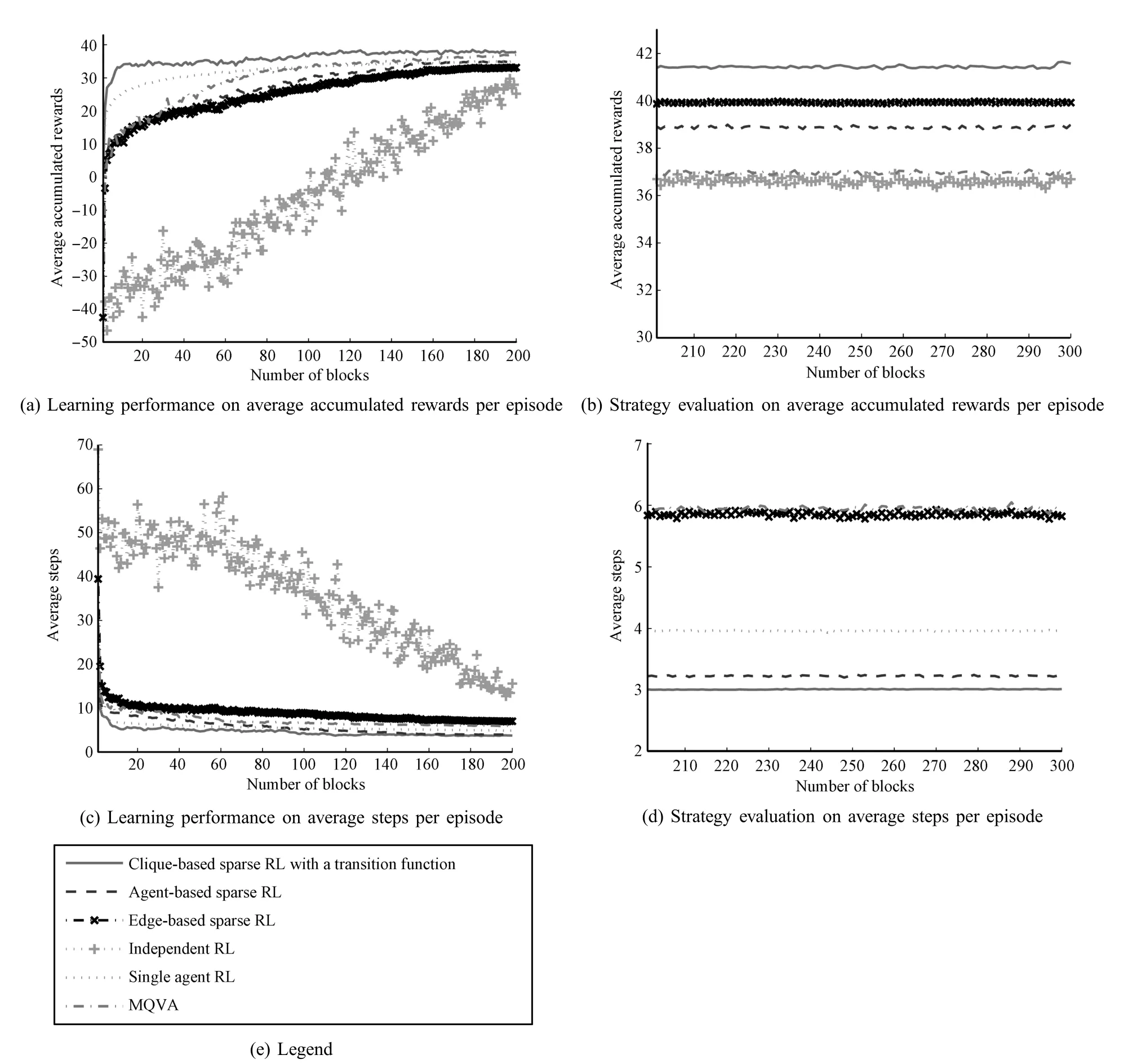
Fig.4. Average reward and steps using different RL.

In the case of sparse RL and the proposed algorithm,although states are partially observable,they still perform well.We think it is benef ted by the characteristics of the DSN problem.The coordination task can be decomposed into subtasks fulf lled by different cliques.This implies that the states needed to fulf ll a subtask are more important for a clique.For example,for agents of Clique 1 to hitand capture a target in Cell 0,the states ofwhether there is a target in Cell 0 and how much energy(1,2,or 3)is left are much more important than those of whether there is a target in Cell 1 or 2.Thismightbe the reason why sparse RL and the proposed algorithm can perform well in the DSN problem even if only local states are available.

VI.CONCLUSION

In this paper,we dealw ith the problem of how to achieve the cooperation in the DSN problem.First,we combine sparse RL w ith a transition function.Second,we presentclique-based decomposition as a method to assign credit among agents.Third,we use the generalmax-plusalgorithm in a factorgraph to acquire the greedy joint action.In this way,each agent needs only to sense local environmentand communicatew ith its neighbors.Furthermore,the local Q-value functions can contain more than two variables,which means,more fexible decomposition can be considered according to the problem.Compared w ith other MARL algorithms,the proposed algorithm gains the best learning performance and produces the best strategies for the DSN problem.

We believe that the bestway for the decomposition depends greatly on the problem concerned.In the DSN problem,by splitting sensors into cliques,we formulate a factor graph which can be easily converted to a loop-free one.In more complicated MAS,a factor graph probably has many loops,which makes the convergence and stability of the general max-plus algorithm not hold any more.In the future,we w ill exam ine the feasibility and effectiveness of the proposed algorithm inmore applications such as coordination of traff c signal lights in an artery and try to solve the problem of factor graphs containing loops.

ACKNOW LEDGEMENT

The authors thank Prof.Nikos V lassis and Jelle.R.Kok for their foundation work on sparse RL.We thank Prof.Derong Liu and Prof.Cesare Alippi for their constructive comments and suggestions on the paper.We thank all the guest editors of the special issue and every member of editorial board for supporting us.We thank Yuzhu Huang,Yujie Dai and Zhongpu Xia for typesetting w ith Latex.

[1]Russell S J,Norvig P,Canny JF,Malik JM,Edwards D D.Artifcial Intelligence:A M odern Approach.Englewood Cliffs:Prentice Hall,1995.

[2]Zhao D B,Dai Y J,Zhang Z.Computational intelligence in urban traff c signal control,a survey.IEEE Transactions on System,Man and Cybernetics PartC:Applications and Reviews,2012,42(4):485−494

[3]Li T,Zhao D B,Yi JQ.Adaptive dynamic programming for multiintersections traff c signal intelligent control.In:Proceedings of the 11th IEEE International Conference on Intelligent Transportation Systems.Beijing,China:IEEE,2008.286−291

[4]Zhao D B,Bai X R,Wang F Y,Xu J,Yu W S.DHP for coordinated freeway ramp metering.IEEETransactions on Intelligent Transportation Systems,2011,12(4):990−999

[5]V lassis N.A concise introduction tomultiagent systems and distributed artif cial intelligence.Synthesis Lectures on Artifcial Intelligence and Machine Learning,2007,1(1):1−71

[6]Khan Z,Glisic S,DaSilva L A,Lehtomaki J.Modeling the dynamics of coalition formation games for cooperative spectrum sharing in an interference channel.IEEE Transactions on Computational Intelligence and AIin Games,2011,3(1):17−30

[7]Zhao D B,Zhang Z,Dai Y J.Self-teaching adaptive dynamic programm ing for Go-Moku.Neurocomputing,2012,78(1):23−29

[8]Tan CH,Tan K C,Tay A.Dynamic game diff culty scaling using adaptivebehavior-based AI.IEEETransactionson Computational Intelligence and AIin Games,2011,3(4):289−301

[9]Zeng L,Hu G D.Consensus of linear multi-agent systems w ith communication and input delays.Acta Automatica Sinica,2013,39(7):1133−1140

[10]Li T,Fu M Y,Xie L H,Zhang JF.Distributed consensus w ith lim ited communication data rate.IEEE Transactions on Automatic Control,2011,56(2):279−292

[11]Sutton R S,Barto A G.Reinforcement Learning:An Introduction.Cambridge:M IT Press,1998

[12]Wiering M A.Multiagent reinforcement learning for traff c lightcontrol.

In:Proceedings of the 17th International Conference on Machine Learning.Stanford University,US:Morgan Kaufmann,2000.1151−1158

[13]Claus C,Boutilier C.The dynam ics of reinforcement learning in cooperative multiagent systems.In:Proceedings of the 15th National Conference on Artif cial Intelligence and 10th Conference on Innovative Applications of Artif cial Intelligence.Menlo Park,CA:AAAI Press/M IT Press,1998.746−752

[14]Tuyls K,Nowe´ A.Evolutionary game theory andmulti-agent reinforcement learning.The Know ledge Engineering Review,2005,20(1):63−90

[15]Gomes E R,Kowalczyk R.Dynamic analysis ofmultiagent Q-learningw ithε-greedy exploration.In:Proceedings of the26th International Conference on Machine Learning.New York,USA:ACM,2009.369−376

[16]Kianercy A,Galstyan A.Dynam ics of Boltzmann Q-learning in twoplayer two-action games.PhysicalReview E,2012,85(4):1145−1154

[17]Littman M L.Markov games as a framework formulti-agent reinforcement learning.In:Proceedings of the 11th International Conference on Machine Learning.New Brunsw ick,US:Morgan Kaufmann,1994.157−163

[18]Owen G.Game Theory(Second Edition).Orlando,Florida:Academic Press,1982.

[19]Littman M L.Friend-or-foe Q-learning in general-sum games.In:Proceedings of the 18th International Conference on Machine Learning.San Francisco,CA:Morgan Kaufmann,2001.322−328

[20]Hu J L,Wellman M P.Multiagent reinforcement learning:theoretical framework and an algorithm.In:Proceedings of the 15th International Conference on Machine Learning.Madison,Wisconsin,US:Morgan Kaufmann,1998.242−250

[21]Singh S,KearnsM,Mansour Y.Nash convergence of gradient dynam ics in general-sum games.In:Proceedings of the 16th Conference on Uncertainty in Artif cial Intelligence.Stanford University,Stanford,California,US:Morgan Kaufmann,2000.541−548

[22]Bow ling M,Veloso M.Multiagent learning using a variable learning rate.Artifcial Intelligence,2002,136(2):215−250

[23]Zhang Hua-Guang,Zhang Xin,Luo Yan-Hong,Yang Jun.An overviewof research on adaptive dynamic programming.Acta Automatica Sinica,2013,39(4):303−311(in Chinese)

[24]Werbos P J.A menu of designs for reinforcement learning over time.Neural Networks forControl.Cambridge:M IT Press,1990

[25]Liu D R,Wang D,Zhao D B,Wei Q L,Jin N.Neural-networkbased optimal control for a class of unknown discrete-time nonlinear systemsusing globalized dualheuristic programm ing.IEEETransactions on Automation Science and Engineering,2012,9(3):628−634

[26]Huang Y Z,Liu D R.Neural-network-based optimal tracking control scheme for a class of unknown discrete-time nonlinear systems using iterative ADP algorithm.Neurocomputing,2014,125:46−56

[27]Song Rui-Zhuo,Xiao Wen-Dong,Sun Chang-Yin.Optimal tracking control for a class of unknown discrete-time systems w ith actuator saturation via data-based ADPalgorithm.Acta Automatica Sinica,2013,39(9):1413−1420(in Chinese)

[28]Wang D,Liu D R.Neuro-optimal control for a class of unknown nonlinear dynamic systems using SN-DHP technique.Neurocomputing,2013,121(9)218−225

[29]Zhang Ji-Lie,Zhang Hua-Guang,Luo Yan-Hong,Liang Hong-Jing.Nearly optimal control scheme using adaptive dynam ic programm ing based on generalized fuzzy hyperbolic model.Acta Automatica Sinica,2013,39(2):142−148(in Chinese)

[30]Liu D R,Javaherian H,Kovalenko O,Huang T.Adaptive critic learning techniques for engine torque and air-fuel ratio control.IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics,2008,38(4):988−993

[31]Zhao D B,Hu Z H,Xia Z P,A lippi C,Zhu YH,Wang D.Full range adaptive cruise control based on supervised adaptive dynamic programm ing.Neurocomputing,2014,125:57−67

[32]Zhao D B,Yi J Q,Liu D R.Particle swarn optimized adaptive dynam ic programm ing.In:Proceedings of the 2007 IEEE International Symposium on Approximate Dynamic Programming and Reinforcement Learning.Honolulu,Hawaiian Islands,US:IEEE,2007.32−37

[33]Crites R H,Barto A G.Improving elevator performance using reinforcement learning.In:Proceedings of Advances in Neural Information Processing Systems 8.Denver,US:M IT Press,1996.1017−1023

[34]Bazzan A L,de Oliveira D,de Silva B C.Learning in groups of traff c signals.Engineering Applications ofArtifcial Intelligence,2010,23(4):560−568

[35]Bazzan A L.Coordinatingmany agents in stochastic games.In:Proceedings of the 2012 International Joint Conference on Neural Networks.Brisbane,Australia:IEEE,2012.1−8

[36]Kok JR,V lassis N.Sparse cooperative Q-learning.In:Proceedings of the 21st International Conference on Machine Learning.USA:ACM,2004.481−488

[37]Kok J R,Vlassis N.Using the max-plus algorithm for multiagent decisionmaking in coordination graphs.In:Proceedingsof RobotSoccer World Cup IX,Lecture Notes in Computer Science.Berlin:Springer,2005.1−12

[38]Syed A,Koenig S,Tambe M.Preprocessing techniques for accelerating the DCOP algorithm ADOPT.In:Proceedings of the 4th International Joint Conference on Autonomous Agents and Multiagent Systems.Utrecht,The Netherlands:ACM,2005.1041−1048

[39]Kok JR,V lassis N.Collaborative multiagent reinforcement learning by payoff propagation.JournalofMachine Learning Research,2006,7(S1):1789−1828

[40]Schneider J,Wong W K,Moore A,Riedmiller M.Distributed value functions.In:Proceedings of the 16th International Conference on Machine Learning.San Francisco,CA:Morgan Kaufmann,1999.371−378

[41]Chen G,Cao W H,Chen X,Wu M.Multi-agent Q-learning w ith joint state value approximation.In:Proceedings of the 30th Chinese Control Conference.Yantai,China:IEEE,2011.4878−4882

[42]Guestrin C,Lagoudakis M G,Parr R.Coordinated reinforcement learning.In:Proceedings of the 19th International Conference on Machine Learning.Sydney,Australia:Morgan Kaufmann,2002.227−234

[43]Panait L,Luke S.Cooperative multi-agent learning:the state of the art.Autonomous Agentsand Multi-Agent Systems,2005,11(3):387−434

[44]Luke S.Genetic programm ing produced competitive soccer softbot teams for RoboCup97.In:Proceedings of the 3rd Annual Conference on Genetic Programm ing.Madison,Wisconsin,US:Morgan Kaufmann,1998.214−222

[45]Kschischang F R,Frey B J,Loeliger H A.Factor graphs and the sum-productalgorithm.IEEETransactionson Information Theory,2001,47(2):498−519

[46]Pearl J.Probabilistic Reasoning in Intelligent Systems.San Mateo:Morgan Kaufman,1988

[47]Weiss Y,Freeman W T.On the optimality of solutions of the maxproduct belief-propagation algorithm in arbitrary graphs.IEEETransactions on Information Theory,2001,47(2):736−744

[48]Lan X,Roth S,Huttenlocher D,Black M.Eff cient belief propagation w ith learned higher-order Markov random f elds.In:Proceedings of the 2006 European Conference on Computer Vision.Berlin:Springer,2006.269−282

[49]Som P,Chockalingam A.Damped belief propagation based near-optimal equalization of severely delay-spread UWB M IMO-ISI channels.In:Proceedings of the 2010 IEEE International Conference on Communications.Cape Town,South Africa:IEEE,2010.1−5

[50]Frey B J,Kschischang F R,Conference A.Probability propagation and iterative decoding.In:Proceedings of the 34th Annual Allerton Conference on Communication Control and Computing.Illinois,US:IEEE,1996.1−4