Closed-loop P-type Iterative Learning Control of Uncertain Linear Distributed Parameter Systems

Xisheng Dai Senping Tian Yunjian Peng Wenguang Luo

I.INTRODUCTION

I TERATIVE learning control(ILC)is an intelligent control method of humanoid thinking,which is especially suitable for dynam ic processes or systemsw ith the repetitive operation characteristics over a finite time interval[1].Themain feature of ILC is thatitcan improve the tracking accuracy by adjusting the system input signal from one repetition cycle to another based on the error observation in each cycle.In addition,ILC has an advantage that it can design the controller w ith the imprecise dynam ic characteristics of the controlled object or w ithout any model.Currently,ILC is playing an important role in practice,such as robotic manipulator[2],intelligent transportation systems[3−4],biomedicine[5],etc.

Meanwhile,ILC is a branch of an intelligent control w ith strictmathematical description,and one of its basic research issues is to design the learning algorithm and analyze its convergence.Nowadays,the research results of iterative learning control on ordinary differential systems and difference systems are very fruitful.The research objects of ILC include linear systems,nonlinear systems,time-delay systems,fractional order systems,discrete systems,singular systems,etc.In terms of iterative learning control algorithm,there are P,D,PD,PID algorithms and their corresponding openloop algorithms,close-loop algorithms,high-order algorithms,etc.(see[1],[6-14]).However,there are notmany research results of ILC for distributed parameter systems described by the partial differential equations.In[15],a fi rst order hyperbolic distributed parameter system was discussed,using a set of ordinary differential equations to approximate the studied partial differential equations and designing the P-type iterative learning algorithm for the ordinary differential system such that the close-loop system is stable and satisfies the appropriate performance index.A class of second order hyperbolic elastic system was studied in[16],by using the differential difference iterative learning algorithm.In[17],P-type and D-type iterative learning algorithms based on sem igroup theory were designed for a class of parabolic distributed parameter systems.Tension control system was studied in[18]by using the PD-type learning algorithm.In[19],by employing the P-type learning control algorithm,a class of single-input single-output coupling(consisting of the hyperbolic and parabolic equations)nonlinear distributed parameter systems were studied and convergence conditions,speed and robustness of the iterative learning algorithm were discussed.Recently,w ithoutany simplification ordiscretization of the3D dynam ics in the time,space as well as iteration domain,the ILC fora classof inhomogeneousheatequationswasproposed in[20].In addition,in[15]iterative learning for the distributed parameter systemswere specifi cally studied while the learning algorithm was open-loop P-type.However,to the best of our know ledge,the related research achievementon the distributed parameter systemsw ith close-loop learning algorithm has not yet appeared.

The close-loop iterative learning algorithm was fi rst proposed in[21],which was used by many scholars for the iterative learning control problem of ordinary differential or difference systems later[11].The main characteristic of the close-loop iterative learning algorithm is to control signals associated w ith the currenterror information,which is different from open-loop iterative learning algorithm.

In thispaper,a close-loop P-type iterative learning algorithm is proposed for linear parabolic distributed parameter systems,which coversmany important industrial processes such as heat exchanger,industrialchem ical reactorand biochem ical reactor.And a complete proof of the convergence of iterative error is given.The main contributions in the paper are:1)it is the fi rst to use the close-loop learning algorithm to research distributed parameter system;2)tracking error convergence analysis is given in detail,which involves three different domains:time,space,and iteration;3)Employing difference method forpartialdifferentialequations,itgives the simulationexamples.

II.PROBLEM STATEMENT AND NEW ALGORITHM

Consider an uncertain linear parabolic distributed parameter system w ith repetitive operation characteristics as follows[8]:

where subscriptkdenotes the iterative number of the process;xandtrespectively denote space and time variables,(x,t)∈Ω×[0,T];Ωis a bounded open subsetw ith smooth boundary∂Ω;qqqk(·,·)∈Rn,uuuk(·,·)∈Ru,yyyk(·,·)∈Ryare the state vector,input vector and output vector of the system,respectively;A(t),B(t),C(t),G(t)are the bounded time-varying uncertain matrices w ith appropriate dimensions,Dis a bounded positive constant diagonalmatrix,i.e.,D=diag{d1,d2,···,dn},0＜pidi＜ ∞(i=1,2,···,n),andpiare known,is a Laplace operator onΩ.

The corresponding initial and boundary conditions of system(1)are

For the controlled object described by system(1),let the desired output beyyyd(x,t).Now,the aim is to seek a corresponding desired inputuuud(x,t),such that the actual output of system(1)

w ill approximate to the desired outputyyyd(x,t).It is not easy to get the desired control for the system is uncertain.We w illgradually gain the control sequenceuuuk(x,t)by using the learning controlmethod,such that

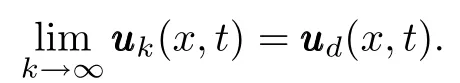
The close-loop P-type iterative learning control algorithm looking for the control input sequenceuuuk(x,t)is

Assume that in the learning process,the system states start from the same initial value,i.e.,

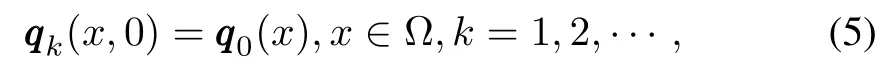
ormore generally,

In this paper,the following notations are used.

For thendimensional vectorW=(w1,w2,···,wn)T,its norm is defined asThe spectrum norm of then×n-order squarematrixAiswhereλmax(·)represents themaximum eigenvalue.

For everyi,ifυi(x)∈Lp(Ω),thenLpnorm andL∞norm of the vector function areυ(x)={υ1(x),υ2(x),···,υn(x)}T

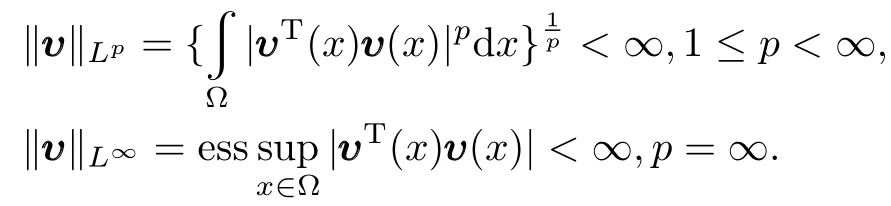
For the positive integerm1 and 1p∞,W m,p(Ω)denotes the Sobolev space constituted by the functionsmtimes differentialandptimes integralonΩ[22].Specially,forυ(x)∈W1,p,define

where∇is the gradient operator.

III.ALGORITHM CONVERGENCE ANALYSIS

Before giving the main results,two lemmas are given as follows[7]:

Lemm a 1.If the constant sequenceconverges to zero,and the sequence(continuous function space defined on[0,T])satisfies

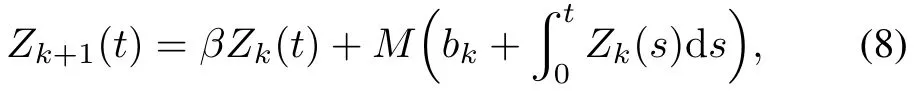
Lemma 2.Iff(t)andg(t)are two continuousnonnegative functions on[0,T],and there exist nonnegative constantsqandMsatisfying

then

Theorem 1.If the gainmatrixΓ(t)in(4)satisfies

then the tracking error converges to zero in meanL2norm,that is,

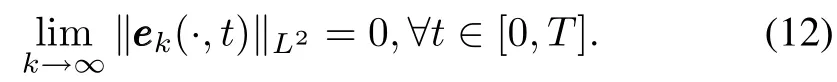
Proof.From algorithm(4)and system(1),it follows that

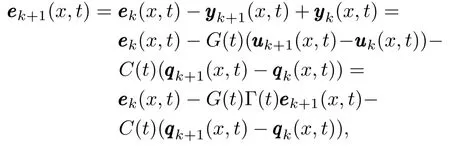
then we have

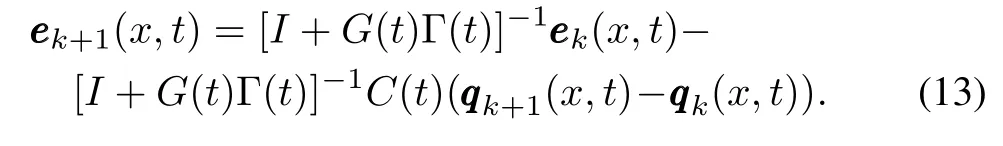
Let

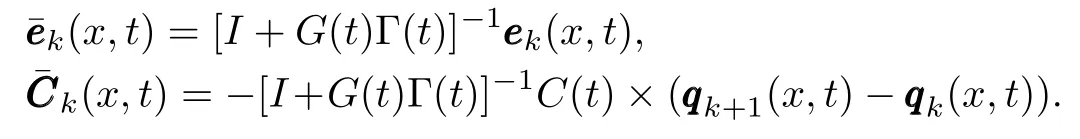
From(13),we have

where

Integrating both sides of(14)toxonΩ,we can get

From(15),if we want to estimatewe have to estimate

From the state equation of system(1),we have

Left-multiplying both sidesof(16)by(qqqk+1(x,t)−qqqk(x,t)¢T.yields

Integrating the above equality forxonΩ,we can obtain

Applying Green formula toI1,we have

Using the boundary condition(2)forI11,we have

For the fixedi,if,then

where tr stands formatrix trace,d=m in{d1,···,dn}.

Using the H¨older inequality forI3,we can get

Therefore,from(18)∼(23)we can get

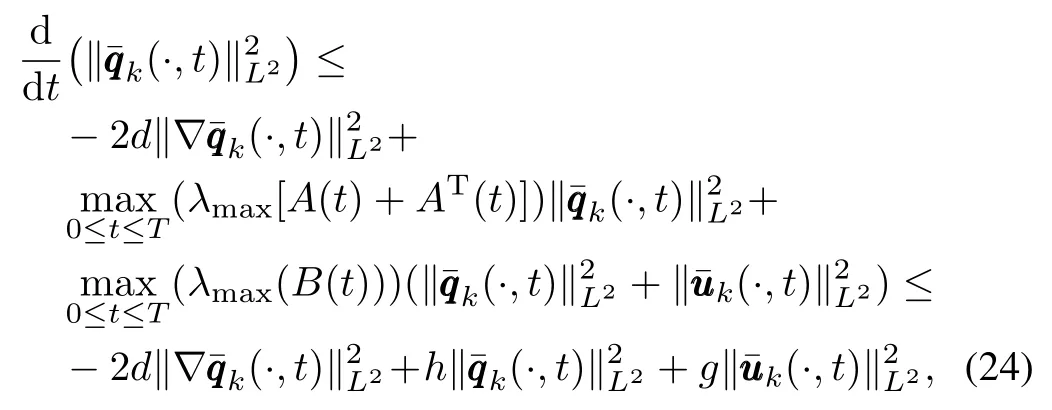
where

Integrating both sides of(24),and then using Bellman-Gronwall inequality,we can get

In addition,from the learning algorithm(4)we can get

where

Moreover,substituting(27)into(15),and using initial conditions(7),we have

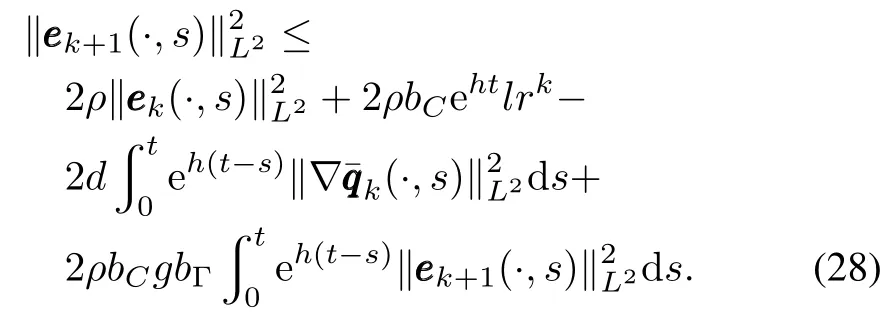
Multiplying both sides of(28)byand noticing that the third item of the right side is less than 0,we have

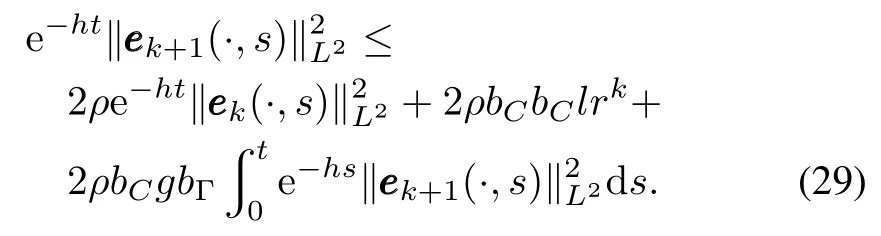
Applying Lemma 2 to(30),we can get

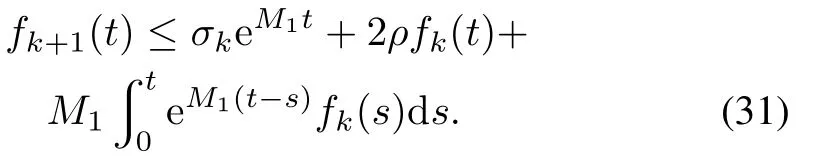
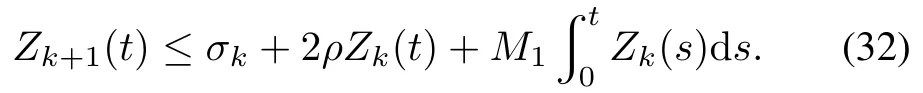
Because when,and from the assumption of Theorem 1,we know 2ρ＜1,thus,applying Lemma 1 to(32),we have

In the end,because

we have

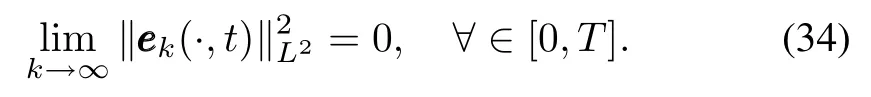
Theorem 2.If the gainmatrixΓ(t)of algorithm(4)satisfies

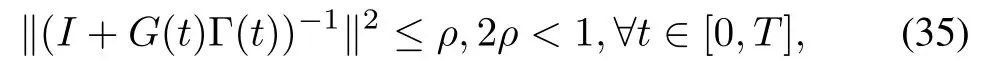
then

Proof.From the definition ofand the conclusion of Theorem 1,we just need to prove

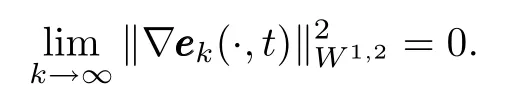
By(13),we have

Sim ilar to the derivation of formula(15),we have

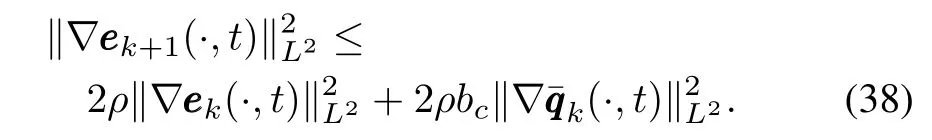
Then

On the other hand,from(28)we have

Multiplying both sides of(40)by e−h tand dividing by 2dleads to

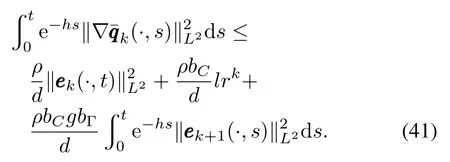
Putting(41)into(39),we have

Let

Then

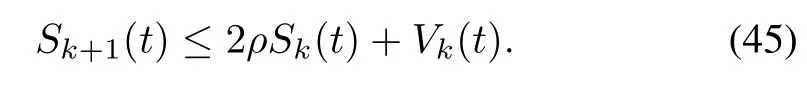
Noticingr＜1,from Theorem 1 and boundedness of,and applying the dom inated convergence theorem to(44),we have

According to(45)and(46),we have

From(43)and(47),by the continuity oftot,theremust be

Therefore,fort∈[0,T],

Theorem 3.If thegainmatrixΓ(t)of algorithm(4)satisfies

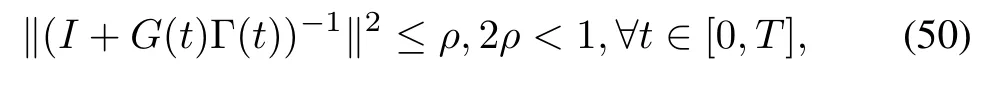
then

Proof.Considering the smoothness offorx,tand boundedness ofΩ,smoothness of∂Ω,boundedness ofandinare bounded.Therefore,andare bounded.

Moreover,usingLpinterpolation inequality,forp≥2,we get

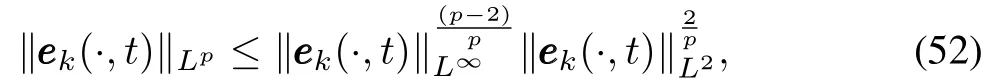
Because of boundedness ofΩ,whenp＞m(wherem=1),by Sobolev embedding theorem(that is,see[22]),we have

whereM=M(Ω,p,m)is constant.The conclusions of Theorems 1 and 2 mean

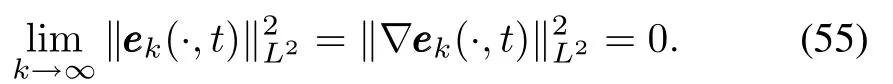
Togetherw ith(52)∼(55),we have

Therefore,

IV.SIMULATION

In order to illustrate the effectiveness of analysis of ILC mentioned in this paper,a specific numerical example considering the follow ing system have been given as follows:

where

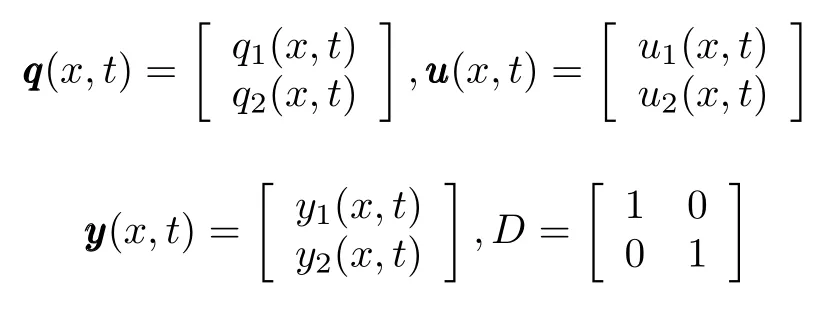
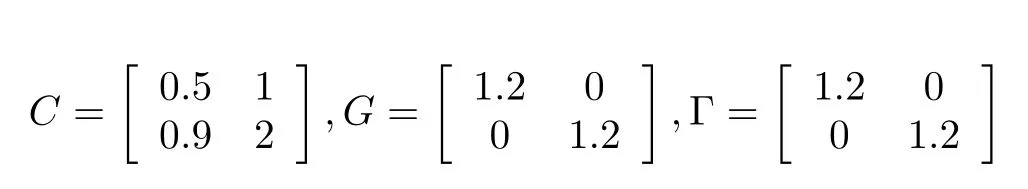
where(x,t)∈[0,1]×[0,0.8],the desired trajectories of the iterative learning aresin,both the initial state value and input value of the controlat the beginning of learning are set0 andr=0,then it iseasy to calculate‖(I+G(t)Γ(t))−1‖2＜0.5,then the condition of Theorem 1(or Theorem 2,Theorem 3)issatisfied,the ILC adopted isbased on close-loop P-type.By the forward differencemethod,the simulation results are shown in Figs.1∼7.

Figs.1 and 2 are the desired curved surfaces,Figs.3 and 4 are relative curved surfaces at the eighth iterations,Figs.5 and 6 are error curved surface.Figs.7 and 8 are the curve charts describing the variation of themaximum tracking error w ith iteration number by using the close-loop ILC and open-loop ILC,respectively.Numerically,when the number of iterations is eight,the absolute values of the maximum tracking error are 1.269×10−3,3.013×10−3by using close-loop ILC,employing open-loop ILC the absolute valuesof themaximum tracking error are 5.096×10−3,1.214×10−3,respectively.Therefore,Figs.1∼7 show that close loop ILC is effective.Meanwhile,from Figs.7 and 8,we can see that the close-loop ILC is superior to the open-loop ILC for systems(58).

Fig.1. Desired output y1d=−2(e−2 t−1)sinπx.

Fig.2. Desired output y2d=−4sint sin 2x.

Fig.3. The eighth iterative output y1k(k=8).

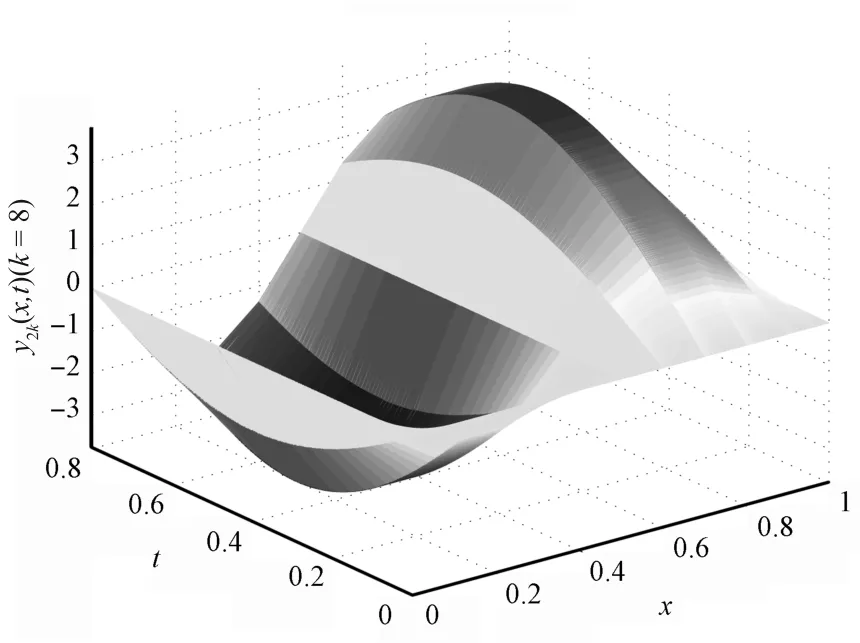
Fig.4. The eighth iterative output y2k(k=8).

Fig.5. Error surface 1:y1d−y1k(k=8).

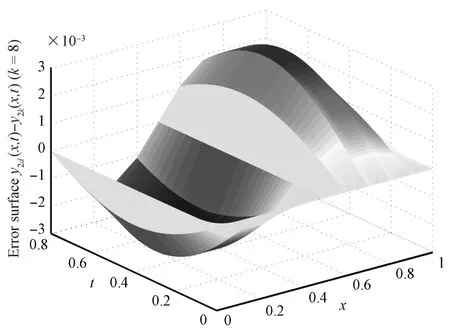
Fig.6. Error surface 2:y2d−y2k(k=8).

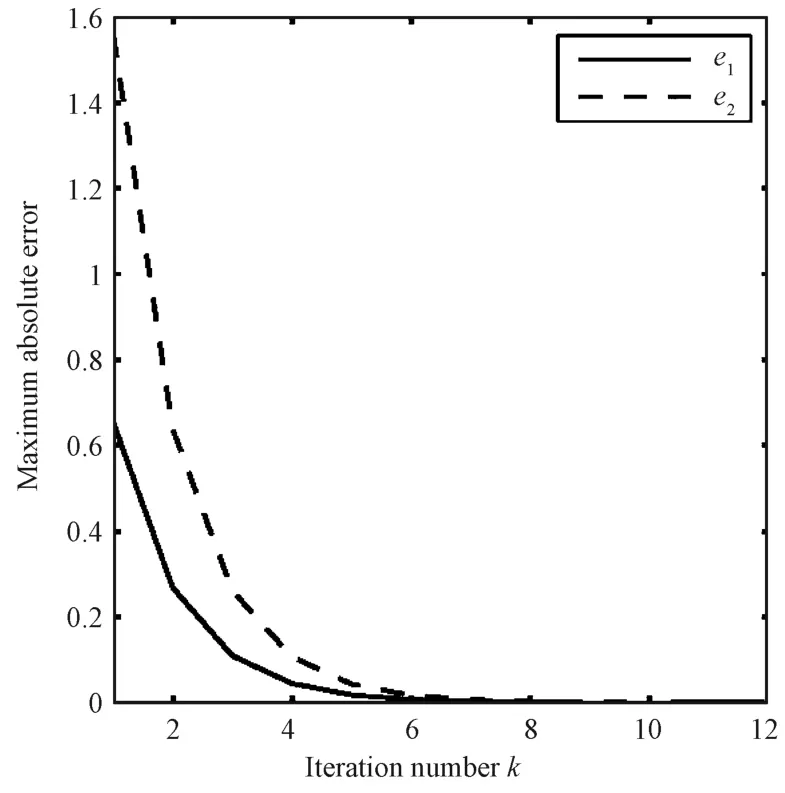
Fig.7. Close-loop iterative number-max tracking error.

Fig.8. Open-loop iterative number-max tracking error.

V.CONCLUSION

A class of parabolic distributed parameter systems,w ith coefficientmatrix uncertain but bounded,is studied by using the close-loop P-type iterative learning algorithm.L2-norms andW1,2-norms of the tracking error convergence analysis is given w ithout any model simplification or discretization.The theoreticalanalysisand simulation results show that the closeloop P-type iterative learning algorithm applicable to ordinary differential systems can be extended to distributed parameter systems.We w ill look formore learning algorithms that can be applied to the distributed parameter systems in the future.

[1]Sun M ing-Xuan,Huang Bao-Jian.Iterative Learning Control.Beijing:National Defence Industry Press,1999.(in Chinese)

[2]Oh SR,Bien Z,Suh I.An iterative learning controlmethod w ith application for robotmanipulator.IEEE JournalofRobotand Automation,1988,4(5):508−514

[3]Hou Z S,Xu JX,Zhong H W.Freeway traffi c control using iterative learning control based ramp metering and speed signaling.IEEETransactions on Vehicular Technology,2007,56(2):466−477

[4]Hou Z S,Wang Y.Term inal iterative learning control based station stop control of a train.International Journal of Control,2011,84(7):1263−1274

[5]Wang Y Q,Dassau E,Doyle III F J.Close-loop control of artificial pancreaticβ-cell in type diabetes mellitus using model predictive iterative learning control.IEEE Transactions Biomedical Engineering,2010,57(2):211−219

[6]Xu JX,Hu Q P,Lee T H,Yamamoto S.Iterative learning controlw ith Sm ith time delay compensator for batch processes.Journal of Process Control,2001,11(3):321−328

[7]Lin Hui,Wang Lin.Iterative Learning Control.Xi′an:Northwestern Polytechnical University Press,1998.(in Chinese)

[8]Xie Sheng-Li,Tian Sen-Ping,Xie Zheng-Dong.Theory and Application of Iterative Learning Control.Beijing:Science Press,2005.82−102.(in Chinese)

[9]Bien Z,Xu J X.Iterative Learning Control− − −Analysis,Design,Integration and Applications.Boston:K luwer Academ ic Press,1998.

[10]Xu JX,Tan Y.Linear and nonlinear iterative learning control.Series of Lecture Notes in Control and Information Science.Berlin:Springer-Verlag,2003.

[11]Chen Y Q,Wen C Y.Iterative learning control-convergence,robustness and applications.Series of Lecture Notes in Control and Information Science.Berlin:Springer-Verlag,2003.

[12]LiY,Chen Y Q,Ahn H S.Fractional-order iterative learning control for fractional-order linear systems.Asian Journal of Control,2011,13(1):54−63

[13]Piao Feng-Xian,Zhang Qing-Ling,Wang Zhe-Feng.Iterative learning control for a class of singular systems.Acta Automatica Sinica,2007,33(6):658−659.(in Chinese)

[14]Chi R H,Hou Z S.Dual-stage optimal iterative learning control for nonlinearnon-affinediscrete-time system.ActaAutomaticaSinica,2007,32(10):1061−1065

[15]Choi JH,Seo B J,Lee K S.Constrained digital regulation of hyperbolic PDE systems:a learning control approach.Journal of Chemical Engineering,2001,18(5):606−611.

[16]Qu Z H.An iterative learning algorithm for boundary control of a stretched moving string.Automatica,2002,38(1):821−827.

[17]Chao X,Arastoo R,Schuster E.On iterative learning controlof parabolic distributed parameter systems.In:Proceedingsof the17th Mediterranean Conference on Control Automation,Makedonia Palace.Thessaloniki,Greece:IEEE,2009.510−515

[18]Zhao H Y,Rahn C D.Iterative learning velocity and tension control for single span axially moving materials.Journal of Dynam ic System M easure Control,2008,130(5):051003

[19]Huang D Q,Xu JX.Steady-state iterative learning control for a class of nonlinear PDE processes.Journal of Process Control,2011,21(8):1155−1163

[20]Huang D Q,Xu JX,Li X F,Xu C,Yu M.D-type anticipator iterative learning control for a class in homogeneousheatequations.Automatica,2013,49(8):2397−2408

[21]Zeng N,Ying X.Iterative learning control algorithm for nonlinear dynamical systems.Acta Automatica Sinica,1992,18(2):168−176

[22]Evans L C.PartialDifferential Equations.Providence:American Mathematical Society,1998.