Concurrent Learning-based Approximate Feedback-Nash Equilibrium Solution of N-player Nonzero-sum Differential Games

Rushikesh Kamalapurkar Justin R. Klotz Warren E. Dixon

I.INTRODUCTION

C LASSICAL optimal control problems are formulated in Bernoulli form as the need to find a single control input thatminimizes a single cost functional under boundary constraintsand dynam ical constraints imposed by the system[1−2].A multitude of relevant control problems can bemodeled as multi-inputsystems,whereeach input is computed by a player,and each player attempts to influence the system state to minimize its own cost function.In this case,the optimization problem for each player is coupled w ith the optimization problem for other players,and hence,in general,an optimal solution in the usual sense does not exist,motivating the formulation of alternative optimality criteria.

Differential game theory provides solution concepts for many multi-player,multi-objective optimization problems[3−5].For example,a set of policies is called a Nash equilibrium solution to amulti-objective optimization problem if none of the players can improve their outcomes by changing their policies while all the other players abide by the Nash equilibrium policies[6].Thus,Nash equilibrium solutions provide a secure set of strategies,in the sense that none of the players have an incentive to diverge from their equilibrium policies.Hence,Nash equilibrium has been a w idely used solution concept in differential game-based control techniques.

In general,Nash equilibria are not unique.For a closedloop differential game(i.e.,the control is a function of the state and time)w ith perfect information(i.e.,all the players know the complete state history),there can be infinitely many Nash equilibria.If the policies are constrained to be feedback policies,the resulting equilibria are called(sub)game perfectNash equilibria or feedback-Nash equilibria.The value functions corresponding to feedback-Nash equilibria satisfy a coupled system of Hamilton-Jacobi(HJ)equations[7−10].

If the system dynam ics are nonlinear and uncertain,an analytical solution of the coupled HJ equations is generally infeasible;and hence,dynam ic programm ing-based approximate solutionsare sought[11−18].In[16],an integral reinforcement learning algorithm is presented to solve nonzero-sum differential games in linear systems w ithout the know ledge of the drift matrix.In[17],a dynam ic programm ing-based technique is developed to find an approximate feedback-Nash equilibrium solution to an infinite horizonN-player nonzerosum differential game online for nonlinear control-affine systems w ith known dynam ics.In[19],a policy iteration-based method is used to solve a two-player zero-sum game online for nonlinear control-affine systemswithout the know ledge of drift dynam ics.

The methods in[17]and[19]solve the differential game online using a parametric function approximator such as a neuralnetwork(NN)to approximate the value functions.Since the approximate value functions do not satisfy the coupled HJ equations,a set of residual errors(the so-called Bellman errors(BEs))is computed along the state trajectories and is used to update the estimatesof the unknown parameters in the function approximator using least-squares or gradient-based techniques.Sim ilar to adaptive control,a restrictivepersistence of excitation(PE)condition is required to ensure boundedness and convergence of the value function weights.Sim ilar to reinforcement learning,an ad-hoc exploration signal is added to the control signal during the learning phase to satisfy the PE condition along the system trajectories[20−22].

It is unclear how to analytically determine an exploration signal that ensures PE for nonlinear systems;and hence,the exploration signal is typically computed via a simulation-based trial and error approach.Furthermore,the existing online approximate optimal control techniques such as[16−17,19,23]do not consider the ad-hoc signal in the Lyapunov-based analysis.Hence,the stability of the overall closed-loop implementation is notestablished.These stability concerns,along w ith concerns that the added probing signal can result in increased controleffortand oscillatory transients,providemotivation for the subsequent development.

Based on the ideas in recentconcurrent learning-based adap-tive control resultssuch as[24]and[25]thatshow a concurrent learning-based adaptive update law can exploit recorded data to augment the adaptive update laws to establish parameter convergence under conditions milder than PE,this paper extends the work in[17]and[19]to relax the PE condition.In this paper,a concurrent learning-based actor-critic-identifier architecture[23]is used to obtain an approximate feedback-Nash equilibrium solution to an infinite horizonN-player nonzero-sum differential game online,w ithout requiring PE,for a nonlinear control-affine system w ith uncertain linearly parameterized drift dynam ics.

A system identifier is used to estimate the unknown parameters in the drift dynamics.The solutions to the coupled HJ equations and the corresponding feedback-Nash equilibrium policies are approximated using parametric universal function approximators.Based on estimates of the unknown drift parameters,estimates for the BEs are evaluated at a set of preselected points in the state-space.The value function and the policy weights are updated using a concurrent learning-based least-squaresapproach tominimize the instantaneous BEsand the BEs evaluated at pre-selected points.Simultaneously,the unknown parameters in the drift dynam ics are updated using a history stack of recorded data via a concurrent learningbased gradient descent approach.It is shown that under a condition m ilder than PE,uniform ly ultimately bounded(UUB)convergenceof theunknown driftparameters,the value functionweightsand thepolicyweights to their truevaluescan be established.Simulation resultsare presented to demonstrate the performance of the developed technique w ithout an added excitation signal.

II.PROBLEM FORMULATION AND EXACT SOLUTION

Consider a class of control-affinemulti-input systems

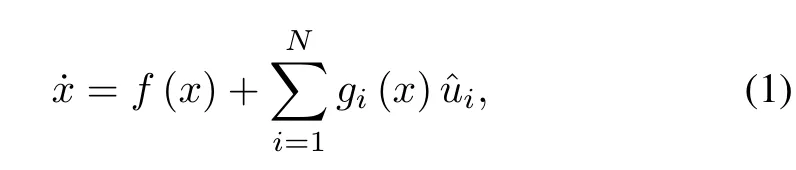
wherex∈Rnis the state andi∈Rm iare the control inputs(i.e.,the players).In(1),the unknown functionf:Rn→Rnis linearly parameterizable,the functiongi:Rn→Rn×m iis known and uniform ly bounded,fandgiare locally Lipschitz,andf(0)=0.Let

be the set of all admissible tuples of feedback policies.Letdenote the value function of theith playerw.r.t.the tuple of feedback policies{u1,···,uN}∈U,defined as

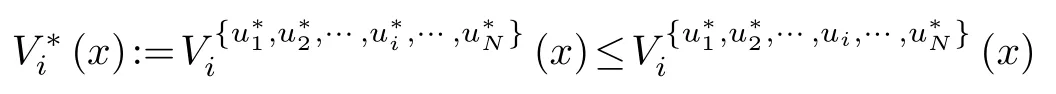
for alluisuch that{u∗1,u∗2,···,ui,···,u∗N}∈U.

The exact closed-loop feedback-Nash equilibrium solutioncan beexpressed in termsof the value functions as[5,8−9,17]

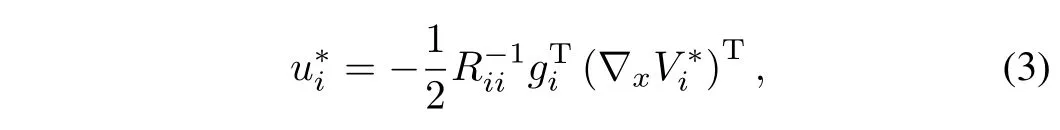
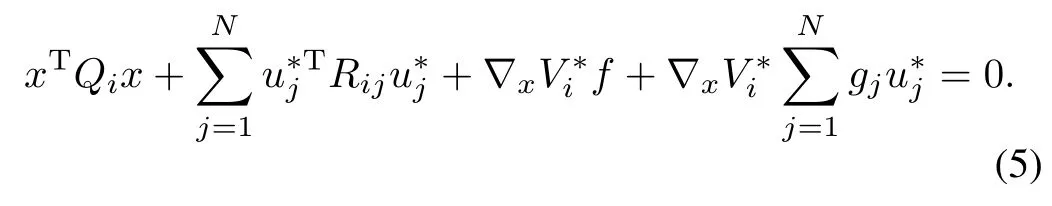
III.APPROXIMATE SOLUTION

Computation of an analytical solution to the coupled nonlinear HJ equations in(4)is,in general,infeasible.Hence,an approximate solutionis sought.Based on,an approximationto the closedloop feedback-Nash equilibrium solution is computed.Since the approximate solution,in general,does not satisfy the HJ equations,a setof residualerrors(the so-called Bellman errors(BEs))is computed as

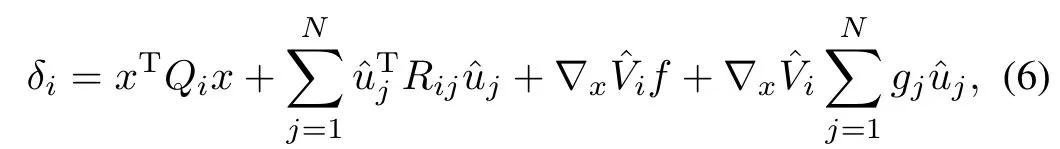
and the approximate solution is recursively improved to drive the BEs to zero.The computation of the BEs in(6)requires know ledge of the drift dynam icsf.To elim inate this requirement,a concurrent learning-based system identifier is developed in the follow ing section.

A.System Identification

Letf(x)=Y(x)θbe the linear parametrization of the drift dynam ics,wheredenotes the locally Lipschitz regression matrix,anddenotes the vector of constant,unknown drift parameters.The system identifier is designed as

where the measurable state estimation erroris defined as:=x−,kx∈Rn×nis a positive definite,constant diagonal observer gain matrix,and∈Rpθdenotes thevector of estimates of the unknown drift parameters.In traditionaladaptive systems,the estimatesare updated tominim ize the instantaneous state estimation error,and convergence of parameter estimates to their true values can be established under a restrictive PE condition.In this result,a concurrent learning-based data-driven approach is developed to relax the PE condition to aweaker,verifiable rank condition as follows.

Assum ption 1[24−25].A history stack Hidcontaining state-action tuples'¡xj,1j,···Nj,¢|j=1,···,Mθrecorded along the trajectoriesof(1)isavailable a priori,such that

where Yj=Y(xj),and pθdenotes the number of unknown parameters in the drift dynam ics.

To facilitate the concurrent learning-based parameterupdate,numerical methods are used to compute the state derivativejcorresponding to(xj,j).The update law for the drift parameter estimates is designed as

where gij:=gi(xj),Γθ∈ Rp×pisa constantpositivedefinite adaptation gain matrix,and kθ∈ R is a constant positive concurrent learning gain.The update law in(9)requires the unmeasurable state derivativej.Since the state derivative at a past recorded point on the state trajectory is required,pastand future recorded values of the state can be used along w ith accurate noncausal smoothing techniques to obtain good estimatesofj.In the presence of derivative estimation errors,the parameter estimation errors can be shown to be UUB,where the size of the ultimate bound depends on the error in the derivative estimate[24].

To incorporatenew information,thehistory stack isupdated w ith new data.Thus,the resulting closed-loop system is a sw itched system.To ensure the stability of the sw itched system,the history stack is updated using a singular value maxim izing algorithm[24].Using(1),the state derivative can be expressed as

and hence,the update law in(9)can be expressed in the advantageous form

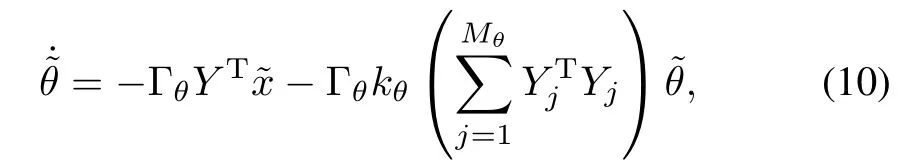
B.Value Function Approximation

The value functions,i.e.,the solutions to the HJequations in(4),are continuously differentiable functions of the state.

Using the universal approximation property of NNs,the value functions can be represented as

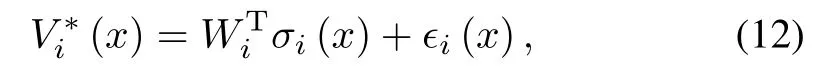
where Wi∈RpWi denotes the constant vector of unknown NN weights,σi:Rn→ RpWi denotes the known NN activation function,pWi∈N denotes the number of hidden layerneurons,and†i:Rn→ R denotes theunknown function reconstruction error.The universal function approximation property guarantees that over any compact domain C⊂Rn,for all constantsthere exist a set of weights and basis functions such thatandare positive constants.Based on(3)and(12),the feedback-Nash equilibrium solutions are given by

The NN-based approximations to the value functions and the controllers are defined as

Assum ption 2.For each i∈ {1,···,N},there exista finite set of Mxipoints{xij∈ Rn|j=1,···,Mxi}such that for all t∈ R≥0,

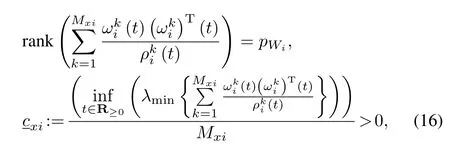
whereλmindenotes the m inimum eigenvalue,and cxi∈R is a positive constant.In(16),where the superscript ik indicates that the term is evaluated at x=xik,and:=where νi∈ R＞0is the normalization gain and Γi∈ RPWi×PWiis the adaptation gain matrix.

The concurrent learning-based least-squares update law for the value function weights is designed as

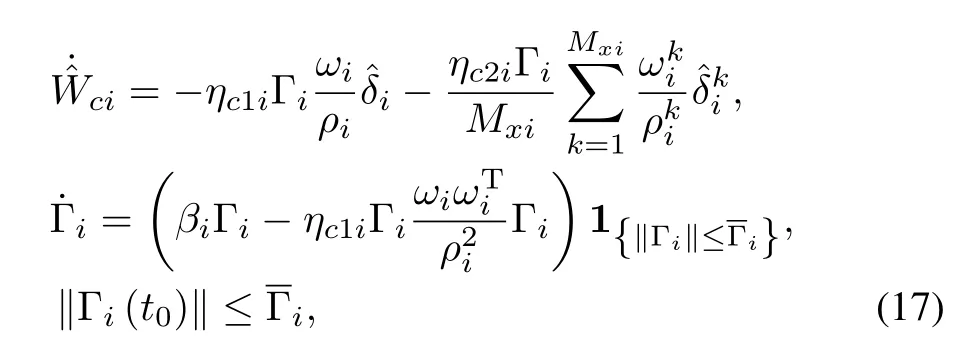
The policy weight update laws are designed based on the subsequent stability analysis as

whereηa1i,ηa2i∈R are positive constant adaptation gains.The forgetting factorβialongw ith the saturation in theupdate law for the least-squares gain matrix in(17)ensure that the least-squares gainmatrixΓiand its inverse is positive definite and bounded for alli∈{1,···,N}as[26]

IV.STABILITY ANALYSIS

Subtracting(4)from(15),the approximate BE can be expressed in an unmeasurable form as

Substituting forV∗andu∗from(12)and(13)and usingf=Yθ,the approximate BE can be expressed as

Sim ilarly,the approximate BE evaluated at the selected points can be expressed in an unmeasurable form as

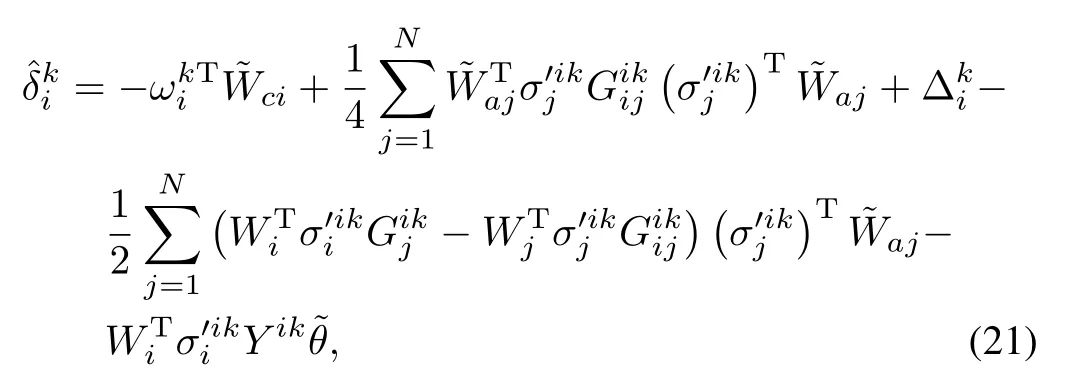
SinceVi∗are positive definite,the bound in(19)and Lemma 4.3 in[27]can be used to bound the candidate Lyapunov function as

whereydenotes the minimum eigenvalue of,qidenotes the m inimum eigenvalue ofQi,kxdenotes the m inimum eigenvalue ofkx,and the suprema exist sinceis uniform ly bounded for allZ,and the functionsGi,Gij,σi,andare continuous.In(24),denotes the Lipschitz constant such thatfor all.The sufficient conditions for UUB convergence are derived based on the subsequent stability analysis as

R are known positive adjustable constants.

Since the NN function approximation error and the Lipschitz constantLYdepend on the compact set that contains the state trajectories,the compact set needs to be established before the gains can be selected using(25).Based on the subsequent stability analysis,an algorithm is developed to compute the required compact set(denoted by)based on the initial conditions.In A lgorithm 1,the notationfor any parameterdenotes the value ofcomputed in theith iteration.Since the constantsιandvldepend onLYonly through the productsand,Algorithm 1 ensures that

Theorem 1.Provided Assumptions 1∼2 hold and the control gains satisfy the sufficient conditions in(25),where the constants in(24)are computed based on the compact setselected using A lgorithm 1,the system identifier in(7)along w ith the adaptive update law in(9),and the controllers in(14)along w ith the adaptive update laws in(17)and(18)ensure that the statex,the state estimation error,the value function weightestimation errorsiand the policy weightestimation errorsaiare UUB,resulting in UUB convergence of the policiesito the feedback-Nash equilibrium policies.

Proof.The derivative of the candidate Lyapunov function in(22)along the trajectories of(1),(10),(11),(17),and(18)is given by

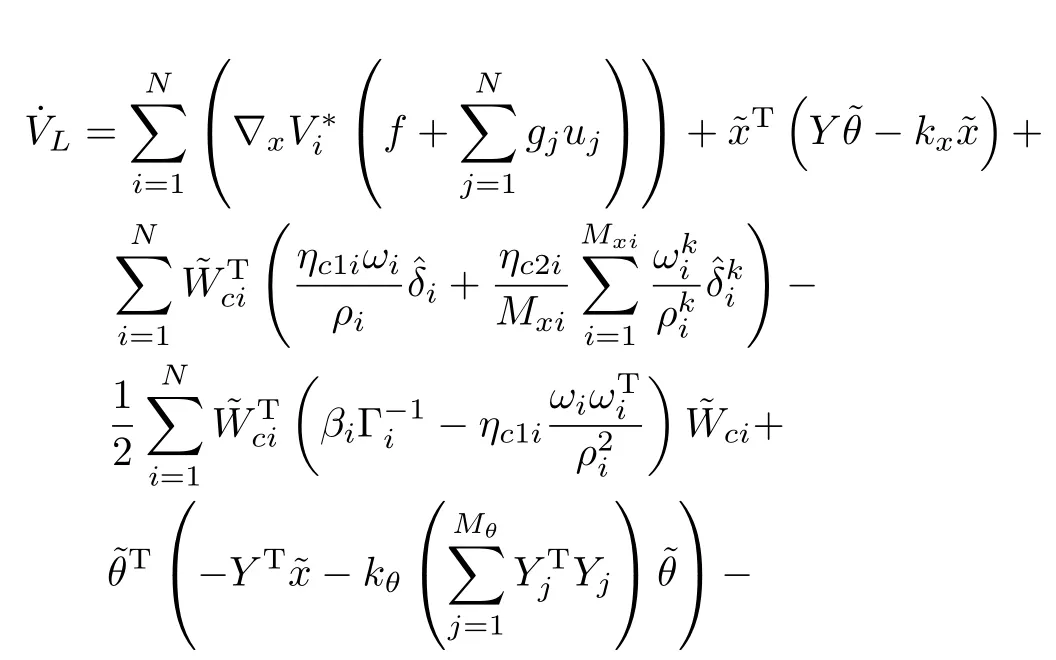
Substituting the unmeasurable forms of the BEs from(20)and(21)into(27),and using the triangle inequality,the Cauchy-Schwarz inequality and Young′s inequality,the Lyapunov derivative in(27)can be bounded as

Provided the sufficient conditions in(25)hold and the conditions

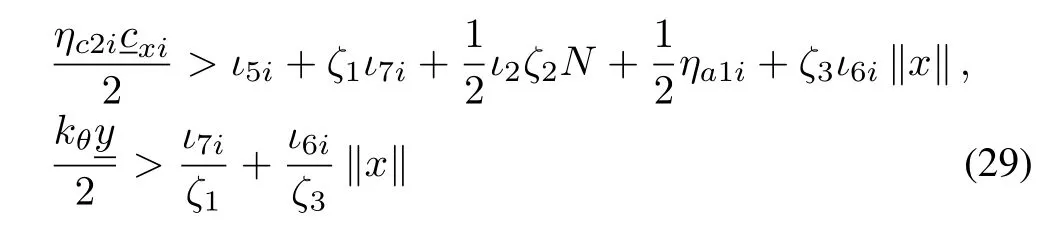
hold for allt∈R≥0.Completing the squares in(28),the bound on the Lyapunov derivative can be expressed as

Using(23),(26),and(30),Theorem 4.18 in[27]‡can‡be·i·nvoked to conclude that limt→∞sup.

Furthermore,the system trajectoriesare bounded asZfor all.Hence,the conditions in(25)are sufficient for the conditions in(29)to hold for all.

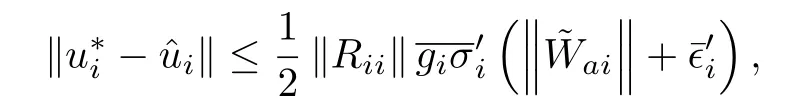
The error between the feedback-Nash equilibrium policy and the approximate policy can be expressed as for alli=1,···,N,where.Since the weightsaiare UUB,UUB convergence of the approximate policies to the feedback-Nash equilibrium policies isobtained.

Remark1.The closed-loop system analyzed using the candidate Lyapunov function in(22)isa sw itched system.The sw itching happenswhen the history stack isupdated and when the least-squares regressionmatricesΓireach their saturation bound.Similar to leastsquares-based adaptive control[26],(22)can be shown to be a common Lyapunov function for the regression matrix saturation,and the use of a singular value maxim izing algorithm to update the history stack ensures that(22)is a common Lyapunov function for the history stack updates[24].Since(22)is a common Lyapunov function,(23),(26)and(30)establish UUB convergence of the sw itched system.

V.SIMULATION

A.ProblemSetup

To portray the performance of the developed approach,the concurrent learning-based adaptive technique is applied to the nonlinear control-affine system[17]

wherex∈R2,u1,u2∈R,and

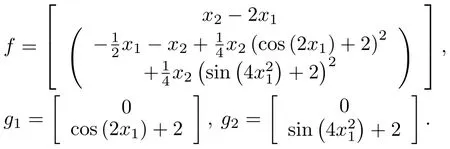
The value function has the structure shown in(2)w ith the weightsQ1=2Q2=2I2andR11=R12=2R21=2R22=2,whereI2is a 2×2 identity matrix.The system identification protocol given in Section III-A and the concurrent learning-based scheme given in Section III-B are implemented simultaneously to providean approximate online feedback-Nash equilibrium solution to the given nonzero-sum two-player game.

B.AnalyticalSolution

The control affine system in(31)is selected for this simulation because it is constructed using the converse HJ approach[28]such that the analytical feedback-Nash equilibrium solution of the nonzero-sum game is

and the feedback-Nash equilibrium control policies for Player 1 and Player 2 are

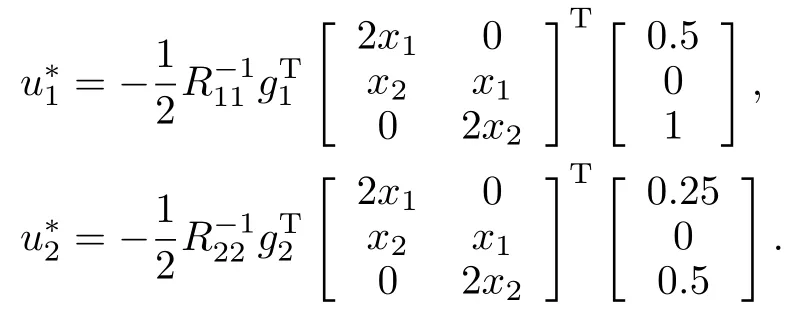
Since the analytical solution is available,the performance of the developed method can be evaluated by comparing the obtained approximate solution against the analytical solution.

C.SimulationParameters

The dynam ics are linearly parameterized asf=Y(x)θ,where

is known and the c⁄onstant vector of parametersθ=is assumed to be unknown.The initial guess forθis selected as

The system identification gains are chosen askx=5,Γθ=diag{20,20,100,100,60,60},kθ=1.5.A history stack of 30 poin[t2s4]is selected using a singular value maximizing algorithm for the concurrent learning-based update law in(9),and the state deriva[t2i9v]es are estimated using a fi fth order Savitzky-Golay fi lter.Based on the structure of the feedback-Nash equilibrium value functions,the basis function for value function approximation is selected as,and the adaptive learning parametersand initial conditions are shown for both players in Tables Iand II.Twenty-five points lying on a 5×5 grid around the origin are selected for the concurrent learning-based update laws in(17)and(18).

TABLE I SIMAULATION PARMAMERERS

D.SimulationResults

Figs.1∼4 show the rapid convergence of the actor and critic weights to the approximate feedback-Nash equilibrium values for both players,resulting in the value functions and control policies

Fig.5 demonstrates that(w ithout the injection of a PE signal)the system identification parameters also approximately converge to the correct values.The state and control signal trajectories are displayed in Figs.6 and 7.

TABLE II SIMULATION INITIAL CONDITIONS

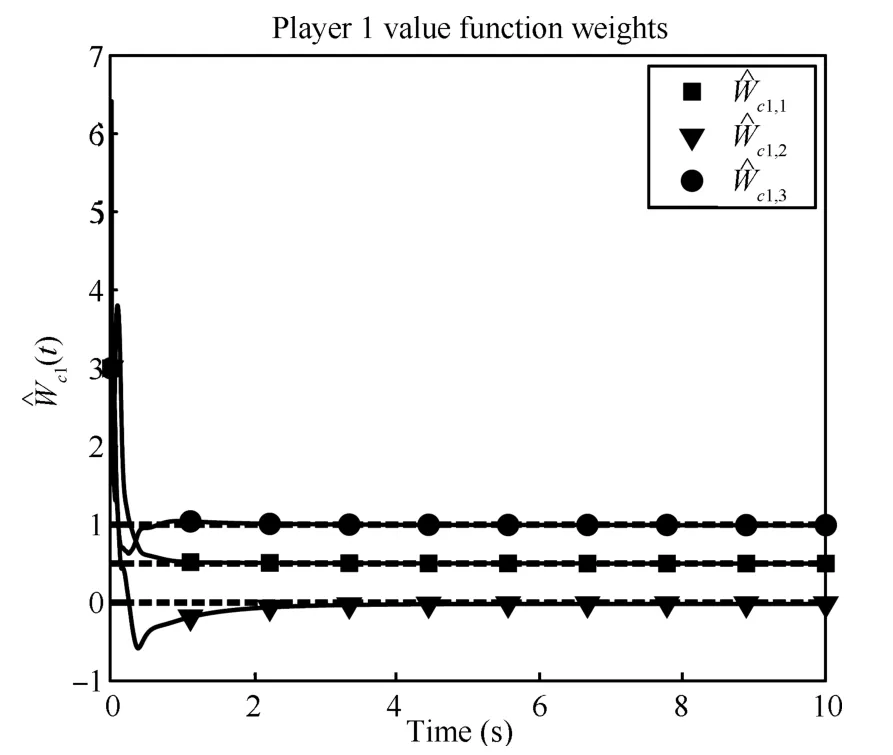
Fig.1. Player 1 critic weights convergence.

Fig.2. Player 1 actor weights convergence.

VI.CONCLUSION

A concurrent learning-based adaptiveapproach isdeveloped to determ ine the feedback-Nash equilibrium solution to anN-player nonzero-sum game online.The solutions to the associated coupled HJequations and the corresponding feedback-Nash equilibrium policies are approximated using parametric universal function approximators.Based on estimates of the unknown driftparameters,estimates for the BEsare evaluated at a set of preselected points in the state-space.The valuefunction and the policy weights are updated using a concurrent learning-based least-squares approach to minimize the instantaneous BEs and the BEs evaluated at the preselected points.Simultaneously,the unknown parameters in the drift dynam ics are updated using a history stack of recorded data via a concurrent learning-based gradient descent approach.

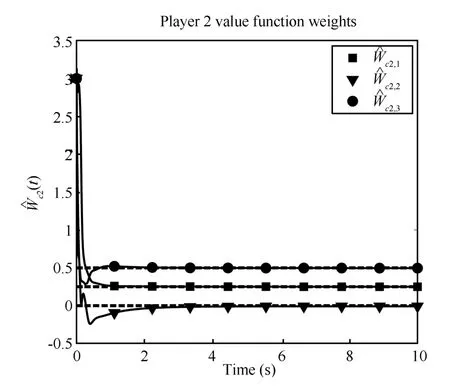
Fig.3. Player 2 critic weights convergence.

Fig.4. Player 2 actor weights convergence.

Fig.5. System identification parameters convergence.

Unlike traditional approaches that require a restrictive PE condition for convergence,UUB convergence of the drift parameters,the value function and policy weights to their true values,and hence,UUB convergence of the policies to the feedback-Nash equilibrium policies,are established under weaker rank conditions using a Lyapunov-based analysis.Simulations are performed to demonstrate the performance of the developed technique.

The developed result relies on a sufficient condition on them inimum eigenvalue of a time-varying regression matrix.While this condition can be heuristically satisfied by choosing enough points,and can be easily verified online,it cannot,in general,be guaranteed a priori.Furthermore,finding a suffi ciently good basis for value function approximation is,in general,nontrivial and can be achieved only through prior know ledge or trial and error.Future research w ill focus on extending the applicability of the developed technique by relieving the aforementioned shortcom ings.

Fig.6. State trajectory convergence to the origin.

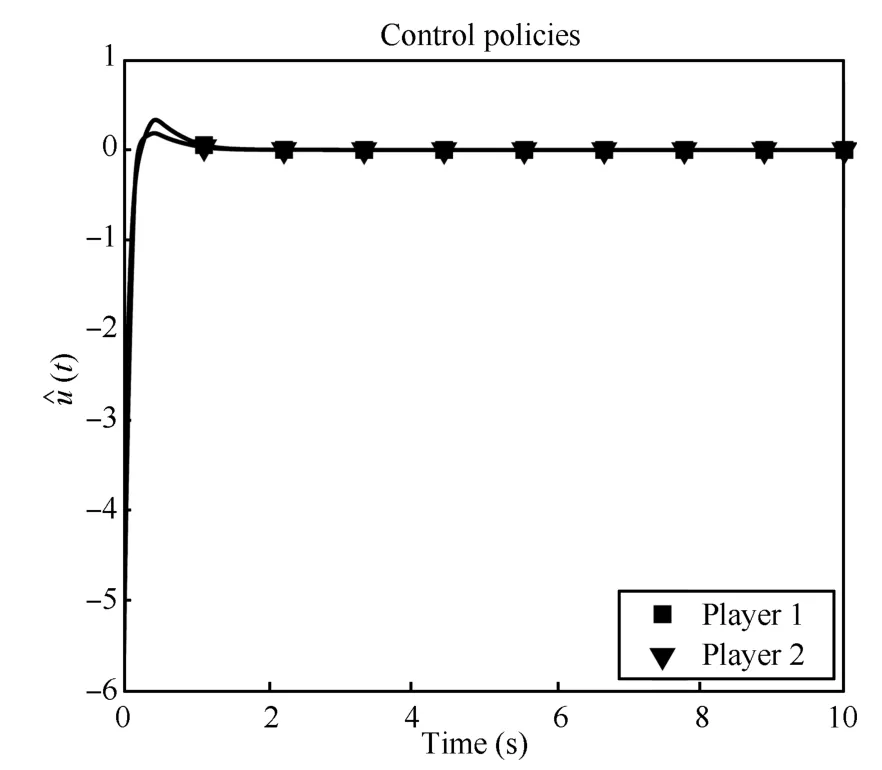
Fig.7. Control policies of Players 1 and 2.

[1]Kirk D E.OptimalControlTheory:AnIntroduction.New York:Dover Publications,2004.

[2]Lew is F L,Vrabie D,Syrmos V L.OptimalControl(Thirdedition).New York:John Wiley&Sons,2012.

[3]Isaacs R.DifferentialGames:AMathematicalTheorywithApplications toWarfareandPursuit,ControlandOptimization.New York:Dover Publications,1999.

[4]Tijs S.IntroductiontoGameTheory.Hindustan Book Agency,2003.

[5]Basar T,Olsder G.DynamicNoncooperativeGameTheory(Second edition).Philadelphia,PA:SIAM,1999.

[6]Nash J.Non-cooperative games.TheAnnalsofMathematics,1951,54(2):286−295

[7]Case JH.Toward a theory of many player differential games.SIAM JournalonControl,1969,7(2):179−197

[8]Starr A W,Ho C Y.Nonzero-sum differential games.Journalof OptimizationTheoryandApplications,1969,3(3):184−206

[9]Starr A,Ho C Y.Further properties of nonzero-sum differential games.JournalofOptimizationTheoryandApplications,1969,3(4):207−219

[10]Friedman A.DifferentialGames.New York:JohnWiley and Sons,1971.

[11]Littman M.Value-function reinforcement learning in Markov games.CognitiveSystemsResearch,2001,2(1):55−66

[12]Wei Q L,Zhang H G.A new approach to solve a class of continuoustime nonlinear quadratic zero-sum game using ADP.In:Proceedings of the IEEE International Conference on Networking Sensing and Control.Sanya,China:IEEE,2008.507−512

[13]Vamvoudakis K,Lew is F.Online synchronous policy iteration method for optimal control.In:Proceedings of the Recent Advances in Intelligent Control Systems.London:Springer,2009.357−374

[14]Zhang H G,Wei Q L,Liu D R.An iterative adaptive dynam ic programmingmethod for solving a class of nonlinear zero-sum differential games.Automatica,2010,47:207−214

[15]Zhang X,Zhang H G,Luo Y H,Dong M.Iteration algorithm for solving the optimal strategies of a class of nonaffine nonlinear quadratic zero-sum games.In:Proceedings of the IEEE Conference Decision and Control.Xuzhou,China:IEEE,2010.1359−1364

[16]Vrabie D,Lew is F.Integral reinforcement learning for online computation of feedback Nash strategies of nonzero-sum differential games.In:Proceedings of the 49th IEEE Conference Decision and Control.Atlanta,GA:IEEE,2010.3066−3071

[17]Vamvoudakis K G,Lew is F L.Multi-player non-zero-sum games:online adaptive learning solution of coupled Ham ilton-Jacobiequations.Automatica,2011,47(8):1556−1569

[18]Zhang H,Liu D,Luo Y,Wang D.AdaptiveDynamicProgramming forControl-AlgorithmsandStability(CommunicationsandControlEngineering).London:Springer-Verlag,2013

[19]Johnson M,Bhasin S,DixonW E.Nonlinear two-player zero-sum game approximate solution using a policy iteration algorithm.In:Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference.Orlando,FL,USA:IEEE,2011.142−147

[20]Mehta P,Meyn S.Q-learning and pontryagin′sm inimum principle.In:Proceedingsof the IEEEConferenceon Decision and Control.Shanghai,China:IEEE,2009.3598−3605

[21]Vrabie D,Abu-Khalaf M,Lew is F L,Wang Y Y.Continuous-time ADP for linear systemsw ith partially unknown dynamics.In:Proceedings of the IEEE International Symposium on Approximate Dynam ic Programm ing and Reinforcement Learning.Honolulu,HI:IEEE,2007.247−253

[22]Sutton R S,Barto A G.ReinforcementLearning:AnIntroduction.Cambridge,MA,USA:M IT Press,1998.4

[23]Bhasin S,Kamalapurkar R,Johnson M,Vamvoudakis K,Lew is F L,Dixon W.A novel actor-critic-identifier architecture for approximate optimal controlof uncertain nonlinearsystems.Automatica,2013,49(1):89−92

[24]Chowdhary G,Yucelen T,M¨uhlegg M,Johnson E N.Concurrent learning adaptive controlof linearsystemsw ith exponentially convergent bounds.InternationalJournalofAdaptiveControlandSignalProcessing,2012,27(4):280−301

[25]Chowdhary G V,Johnson E N.Theory and fl ight-test validation of a concurrent-learning adaptive controller.JournalofGuidance,Control,andDynamics,2011,34(2):592−607

[26]Ioannou P,Sun J.RobustAdaptiveControl.New Jersey:Prentice Hall,1996.198

[27]Khalil H K.NonlinearSystems(Thirdedition).New Jersey:Prentice Hall,2002.172

[28]Nevisti´c V,Primbs J A.Constrained nonlinear optimal control:a converse HJB approach.California Institute of Technology,Pasadena,CA 91125,Techical Report CIT-CDS 96-021,1996.5

[29]Savitzky A,Golay M J E.Smoothing and differentiation of data by simplified least squares procedures.AnalyticalChemistry,1964,36(8):1627−1639