Off-Policy Reinforcement Learning with Gaussian Processes

Girish Chowdhary Miao Liu Robert Grande Thomas Walsh Jonathan How Lawrence Carin

I.INTRODUCTION

R EINFORCEMENT learning(RL)[1]in continuous or large state spaces often relies on function approximation to maintain a compactmodel of the value(Q)function[2−4].The performance of approximate RL algorithms employing fixed feature function approximators,such as radial bases function networks w ith a priori distributed centers,often depends on the choice of those features,which can be difficult to allocate.Gaussian processes(GPs)[5]are Bayesian nonparametric(BNP)models thatare capable of automatically adjusting features based on the observed data.GPs have been successfully employed in high-dimensional approximate RL domains,such as a simulated octopus arm[6],but several aspects of their use,particularly convergence guarantees and off-policy learning have not been fully addressed.

More specifically,unlike RL algorithms employing a tabular representation,and even some function approximation techniques[3,7],no convergence results for RL algorithmsw ith GPs exist.A lso,existing RLmethodsw ith GPshave either required burdensome computation in the form of a planner[8−10]or require that the policy being learned is the same as the one being executed(on-policy learning)[6].The latter approach is less general than off-policy RL,which enables learning the optimal value function using samples collected w ith a safe or exploratory policy.

In this paper,we present a method for approximate RL using GPs thathasprovable convergenceguarantees in the offpolicy setting.More specifically,amodel-free off-policy approximate reinforcement learning technique,termed as GPQ,that uses a GP model to approximate the value function is presented.GPQ does not require a planner,and because it is off-policy,it can be used in both online or batch settings even when the data is obtained using a safe or exploratory policy.In addition,we presentan extension of GPQ thatuses a heuristic exploration strategy based on the GP′s inherent measures on predictive confidence.In addition to presenting the GPQ framework,sufficient conditions for convergence of GPQ to the best achievable optimal Q-function given the data(Q∗)are presented in the batch and online setting,and it is shown that these properties hold even if new features are added or less-important features removed to maintain computational feasibility.Our work also contributes to offpolicy approximate RL in general,because unlike other recent papers on off-policy RL w ith fixed-parameter linear function approximation[4,11−13],our approach allows the basis functions to beautomatically identified from data.Furthermore,our condition for convergence revealswhy in the batch case GPQ or kernel base fi tted Q-Iteration[3]could lead to divergence in the worst case,and how the divergence can be prevented by tuning a regularization-like parameter of the GP.A practical online implementation of this framework thatmakes use of a recent budgeted online sparse GP inference algorithm[14]is empirically demonstrated,and it is theoretically shown how the sparsification affects GPQ′s performance in the batch case.Our theoretical and empirical results show off-policy RL using a GP provides provable convergence guarantees and competitive learning speeds.

II.BACKGROUND

The problem of sequential decision making under uncertainty can be formulated as a Markov decision process(MDP)[1]:〉,w ith state spaceS,action setA,transition functionP=p(st+1|st,at),reward function,and discount factorγ∈[0,1).A deterministic policyπ:S→Pr[A]maps states to actions.Together w ith the initial states0,a policy forms a trajectorywhereand bothrtandstare sampled from the reward and transition functions.

The state-action value function or Q-function of each state P-action pair under policyis defined aswhich is the expected sum of discounted rewards obtained starting from states,taking actionaand follow ingthereafter.The optimal Q-functionQ∗satisfiesand is captured by the Bellman equation=.

Throughout this paper,bounds are derived on||−Q∗||whereis an approximation ofQ∗.Deriving such bounds provides a bound on the value of the optimal policy derived fromwhen it is executed in the realworld,specifically an error factor ofis introduced[15].

A.Reinforcement Learning

Reinforcement learning is concerned w ith finding the optimal policywhenPandRare unknown.In online RL,an agent chooses actions to sample trajectories from the environment.In batch RL,a collection of trajectories is provided to the learning agent.In either case,model-free value-based reinforcement learning methods update an estimate ofQ(s,a)directly based on the samples.When an RL method learns the value function of the same policy w ith which samples were collected,it is classified as on-policy;when the policy employed to obtain samples is different,it is termed off-policy.For instance,the Q-learning algorithm[16]performs an off-policy update of the form,w ith a time dependent learning rateαt¡ and temporal¢ difference(TD)error,wherea′is the action thatmaxim izes.The on-policy counterpart to Q-learning is SARSA[1],which uses a different TD error based on the current policy:.Off-policy algorithms can be used in situations where batch data or“safe”exploration policies are used.

For continuous RL domains,linear value function approximation is often used to model the Q-function as a weighted combination of fixed bases,that is=.Then,the off-policy gradient descent operation from Q-learning can be used to updateθusing the follow ing TD error w ith.However,function approximation can cause divergence foroff-policy RLmethods,including Q-learning and linear-least squares approaches[17−18].It is possible to guarantee convergence of some off-policy algorithms under certain constraints.For instance,Melo et al.[7]provide sufficient conditions for approximate Q-learning′s convergence:.This generally requires the initial policy to be very close toand is heavily tied to the choice of bases.The potential for divergence in off-policy settings can limit the applicability of RL algorithms to safety critical domains.

B.Related Work

A series of papers[2,6]showed GPs could be used to capture thevalue function using on-policy updates,specifically SARSA and approximate policy iteration,which may not be able to learn the value of a new policy from batch data.Others have used GPs in model-based RL to learn the MDP parameters(PandR)[8,10],including a variant of theRmaxalgorithm that explored through an“optimism in the face of uncertainty”heuristic[9].However,model-based approaches require a planner to determ ine the bestaction to takeaftereach update,which could be computationally costly.

Several recentapproaches ensure convergence in the online case by adding some form of regularization to TD algorithms for policy evaluation,as done in TDC[13];GQ[4],LARSTD[11],and RO-TD[12].These algorithms use different versions of the SARSA-style TD error,but the regularization ensures their convergence even when the samples are obtained off-policy.In contrast to these algorithms,the GPQ algorithm presented here is an off-policy learning algorithm that attempts to directly minim ize the Q-learning TD error.This TD error,which is directly derived from the Bellman optimality equations,is better suited for off-policy learning because it is the bestapproximation to the optimalQ-function given the samples that have been seen.Furthermore,many existing approaches rely on a fixed set of bases stipulated at initialization.In particular,[4]assumed the existence of a fixed setof features and Liu etal.[12]assume a fixed setof features from which features of less value are removed.In contrast,GPQ leverages a BNP approach to automatically choose features based on the data.Other algorithms,such as Bellman error basis functions[19]dynam ically construct features for linear function approximators,but thesemethodsare primarily used in on-policy evaluation and,depending on their potential space of features,may not have the representational power of GPs.In the batch case,several algorithms belonging to the fi tted Q-iteration(FQI)family of algorithms[3]can guarantee off-policy convergence w ith specifi c function approximators,including averagers[20]and certain forms of regularized least squares[21].In contrast,ourapproach leveragesGPs,which are powerful BNP function approximators.We show thatGaussian processes can,w ith a prescribed setting of one regularization parameter,guarantee convergence in thebatch case(which can be related to an FQI-like algorithm)and then describe how to extend this batch algorithm to the online case.In the online case,Geistetal.[22]use ameasurementmodel sim ilar to GPQ and FQI,and handle the nonlinearity of thatequation by using extended/unscented Kalman fi lter like approaches,which can potentially diverge.

In Section IV-B,we introduce an explorationmethod based on“optim ism in the face of uncertainty”using GP confidence intervals.Others have used confidence intervals on the MDP parameters themselves in a similar way in the discrete-state case[23].Previous work has done sim ilar exploration using GPs in supervised learning[24]and the bandit setting w ith continuous actions[25],but the latter is only for single-state RL whereas we explore in a full MDP.Other RL exploration heuristics thatutilize GP variance include a strategy based on information theory[26],whichmore explicitly targetsuncertain areas,butwas designed for on-policy RL and requires amodel to calculate long-term information gains.

A lthough rooted in the Bayesian framework,GPs have a deep connection w ith reproducing kernel Hilbert space techniques[5],therefore,thiswork also augments the grow ing body of literature in Kernel based approximate MDPs and RL[27−30].

C.Gaussian Processes

Gaussian processes(GPs)[5]are BNP function approximationmodels:they do notspecify amodel structure a prioriand explicitly model noise and uncertainty.A GP is defined as a collection of random variables,any finite subset of which has a joint Gaussian distribution w ith mean(prediction)functionm(z)and covariance kernel,such as a radial basis function(RBF),k(z′,z),for input points z and z′.In the case of modeling the Q-function,the input domain is the space of all state action pairs and the model captures a distribution over possible Q-functions.

Let Z=[z1,···,zτ]be a setof state action pairs observed at discrete sample times,where each state action pair is concatenated as z for ease of exposition.In our analysis,we assume a finite set of actions,but all analysis extends to the continuous action space as well.Let=[y1,···,yτ]Tdenote the vector of observation values at the respective state action pairs.Given some setof data pointsat corresponding locations in the input domain Z,we would like to predict the expected value of the Q-function yτ+1at some possibly new location zτ+1.Define K(Z,Z)as the kernel matrix w ith entries Kl,m=k(zl,zm).kkk(Z,zτ+1) ∈ Rτdenotes the kernel vector corresponding to theτ+1-thmeasurement,andrepresents the variance of the uncertainty in our measurement.Using Bayes law and properties of Gaussian distributions,the conditional probability can be calculated as a normal variable[5]w ith mean m(zτ+1)= αTkkk(Z,zτ+1),whereare the kernelweights,and covariance

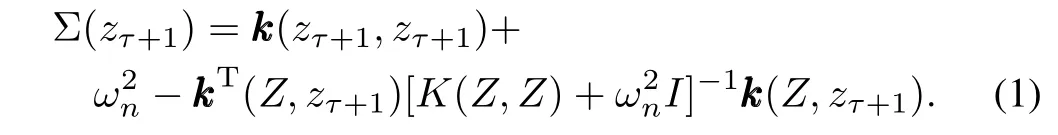
Perform ing batch prediction using GPs requires an expensive inversion of amatrix that scales as O(τ3)w ith the size of the data.Many sparsification schemes have been proposed to reduce this computational complexity to O(τm2)[31−32],where m is a number of reduced parameters.In this paper,we use the sparsification method of[14],which allows for sequential updates.This sparsification algorithm works by building a dictionary of basis vector points that adequately describe the inputdomainw ithoutincluding abasispointat the location of every observed data point.A full description of this algorithm is available in Appendix A.In order to determine when a new point should be added to the dictionary,a linear independence test is performed

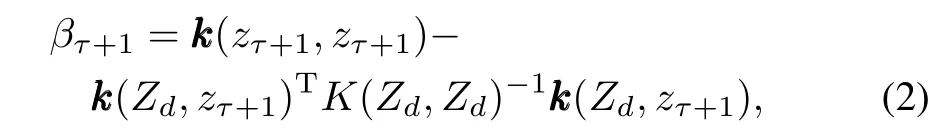
when βτ+1is larger than a specified threshold βtol,then a new data pointisadded to the dictionary.Otherw ise,theweightsατare updated,but the dimensionality ofατremains the same.

III.BATCH OFF-POLICY RLW ITH A GP

As a slight abuse of notation,we let Q∗represent the best possible representation of the true Q-function given the data available.In GPQ,we model Q∗as a GP w ith mean function m∗(s,a)and positive sem i-definite covariance kernel k([s,a],[s′,a′]).To do so,we place a zero mean Gaussian prior on Q,so Q(s,a)∼ N¡0,k(·,·)¢.Our goal is to perform posterior inference using available information so that the current estimate of themeanˆm approaches themean of Q∗.Let the current estimate of the mean of the Q-function be(s,a)=(s,a).Since samples of Q∗are not available,posterior inference needs to be performed using the best estimate of Q∗at the current time as

Everytime we update the model of(st,at)w ith a new observation,the accuracy of the observation is dependent on the accuracy of the currentmodel.Typically,the parameteris viewed as a uncorrelated,Gaussian measurement noise in GP literature.Here,we offer an alternative interpretation ofas a regularization term which accounts for the fact that currentmeasurements are notnecessarily drawn from the true model and therefore prevents ourmodel from converging too quickly to an incorrectestimate of Q∗.Aswew ill show later,plays a pivotal role in preventing divergence.

We now consider using the update rule in(3)w ith a GP model in the batch setting.

Using GPs and the update rule in(3)in the batch setting gives us A lgorithm 1,which we call GP-FQI because it is a member of the fi tted Q-Iteration fam ily of algorithms.Ateach iteration,the values of the stored points are updated based on the stored rewards and transitions as well as the previous iteration′s approximation of the Q-values,which is the form of fi tted Q-iteration.

A lgorithm 1.Batch GPQ(GP-FQI)

1)Input:Experience tuples 〈s,a,r,s′〉1,···,N

2)Output:A GP representingˆQ∗

4)repeat

6)foreach experience tuple 〈s,a,r,s′〉ido

7)yi=ri+γm axb(s′,b)

10)untilthe convergence condition is satisfied

A lgorithm 2.Online GPQ

1)foreach time stepτdo

2) Choose aτfrom sτ,using †-greedy exploration

3) Take action aτ,observe rτ,sτ+1

4)Let zτ=〈s,a〉and yτ=r+γmaxb(s′,b)

5)ifβτ+1＞ βtolthen

6) Add zτto the BV set

7) Compute kzτ+1and ατ+1according to[14]

8)if|BV|＞Budgetthen

9) Delete zi∈BV w ith lowest score according to[14]

While convergence guarantees exist for some function approximators used in FQI,such as regression trees,others,such as neural nets,are known to be potentially divergent.Below,we prove thatGP-FQIcan diverge if the regularization parameter is not properly set.However,we also prove that for any set of hyperparameters and desired density of data,a proper regularization constant can be determined to ensure convergence.We begin w ith a counter-example show ing divergence in the batch setting ifis insufficient,but show convergence whenis large enough.

Consider a system w ith three nodes located along the real line at locations−1,0,and 1.Ateach time step,the agent can move determ inistically to any node or remain at its current node.The reward associated w ith all actions is zero.A ll algorithms are initialized w ith(z)=1,∀z,γ=0.9999,and we use a RBF kernelw ith bandw idthσ=1 in all cases.We consider two settings of the regularization parameter,andFig.1 shows that whenis set too low,the Bellman operation can produce divergence in the batch setting.If the regularization is set to the higher value,GP-FQI converges.In the follow ing sections,we show that determining thesufficient regularization parameterdependsonly on the density of the data and the hyperparameters,not the initialization value oforγ.

Fig.1. Themaximum error‖−Q∗‖is plotted for GP-FQIw ith insufficient regularizationω=0.1 and sufficient regularization ω=1.

LetTdenote theapproximate Bellman operator thatupdates themean of the current estimate of the Q-function using the measurementmodel of(3),that isk+1=Tk,we argue thatTis a contraction,so a fixed point exists.For a GP model,we define the approximate Bellman operator in the batch case as training a new GP w ith the observationsyi=r(si,ai)+γm axb(,b)at the input locationszi=(si,ai).

In the follow ing theorem,we show that in the case of finite data,a finite regularization term always exists which guarantees convergence.In the next theorem,we show that a finite regularization tern exists for a sparse GP that only adds kernels when the tolerance threshold Ptol is excedded.In Theorem 3,we show that a finite bound exists,but do not compute the bound exactly as this depends on the topology of the space and kernel function.

Theorem 1.Given a GPw ith dataZof finite sizeN,and Mercer kernel that is bounded above bykmax,there exists a finite regularization parametersuch thatTis a contraction in the batch setting.In particular,

Proof.Let‖(·)‖denote the infinity norm.Consider the approximate Bellman operatorT

If‖K(Z,Z)‖‖(K(Z,Z)+I)−1‖≤1,thenTis a contraction.By the structure of the kernel,we know‖K(Z,Z)‖=for finite data,the sum is a finite sum of finite numbers,so‖K(Z,Z)‖is finite.For the second term,we assume thatis large and use[33]to bound the infinity norm of an inversematrix that is strictly diagonally dom inant.In order to be considered strictly diagonally dominant,amatrixAmust have the property,∀i.In this case,

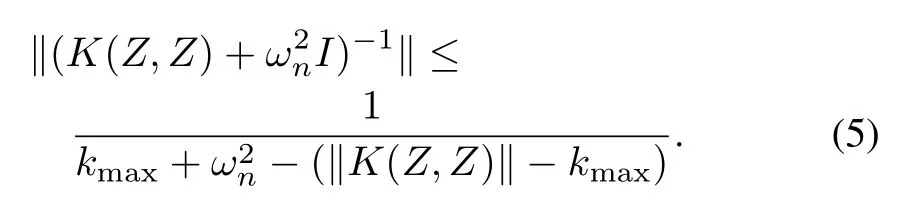
Therefore,settingωn＞2‖K(Z,Z)‖−2kmax,we have

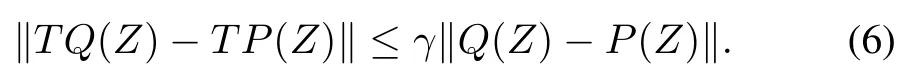
Theorem 2.Given a GPw ith infinite data generated using a sparse approximation w ith acceptance toleranceβtol,and given aMercerkernel function thatdecaysexponentially,there exists a finite regularization parametersuch thatTis a contraction in the batch setting.

Proof.To prove a contraction,we prove that‖K(Z,Z)‖is finite,so by Theorem 1 there exists a finitesuch that(4)is a contraction.The norm of‖K(Z,Z)‖is given by.We argue that the sum is convergent for an infinite numberof data points selected using the linear independence test in(12).As the volume of the input domain increases to infinity,the number of data points added by a sparse selection increases polynom ially,due to Ehrhart′s theorem,while the value they add to the sum decays exponentially fast.Thismeans that the sum is convergent as the number of BV goes to infinity.The result follows from Theorem 1.For details,the reader is referred to Appendix B.1.

Theorem 2 provides a powerful insight into the convergence properties of GPs.As the density of basis vectors increases or as the bandw idth of the kernel function grows,corresponding to decreasingβtol,the basis vector weightsαibecomes increasingly correlated.As the weights become correlated,changing the weight at one basis vector also changes theweights of nearby basis vectors.It is this sharing of weights that can result in divergence,as seen in[17].Theorem 2 shows that for a givenβtoland kernel function,there exists a finite regularization parameterthat w ill preventdivergence,however.This regularization technique can also be applied to provide convergence guarantees for FQI using a linear function approximator.In related work,[34]provides convergenceguarantees for linear FQIusing a sim ilar regularization technique solved using an optim ization-based framework.In practice,does nothave to be set very large to preventdivergence.Both Theorem 2 and[34]considerworst case analysis,which generally is not encountered in practice.

For most applications,reasonable values of∈[0.01,1]w ill prevent divergence.In the next theorem,we bound the approximation error from using a sparse representation of a GP versus a full GP.

Theorem 3.If the sparse GP algorithm is used,the error‖E[−Q∗]‖is uniform ly,ultimately bounded for the approximate Bellman operator.

Proof.Let(st,at)=tfor notational convenience.Letbe a positive definite Lyapunov candidate.LetTdenote the approximate Bellman operator applied to a sparse GP.

In the proof of Theorem 3,it should be noted thatqt∞is alwaysupper bounded.In particular,[35]shows that theupper bound onqt∞depends on the sparsification tolerance†to lin the online GP algorithm in[14].

IV.ONLINE LEARNING WITH GPQ

In the online case,an agentmust collect data on its own,and the set of samples w ill increase in size.First consider a naive implementation of GP-FQIin theonline setting inwhich at every step,we run the GP-FQIalgorithm to convergence.This leads to the follow ing changes to GP-FQI:

1)At each timestept,the greedy actiona∗=arg maxa(st,a)is selected w ith probability 1−†,and w ith probability†a random action is chosen.

2)After each〈s,a,r,s′〉experience,GPais updated by adding the points,a,r+γmaxb(s′,b).Determineusing Theorem 1 and perform GP-FQIas in Algorithm 1.

In the batch sequential version of GP-FQI,can be determ ined ateach step by directly computing‖K(Z,Z)‖.A lternatively,one can use the linear independence testand only accept data points w ithGiven this know ledge,‖K(Z,Z)‖can be computed a priori.

Corollary 1.If Theorem 1 and Theorem 2 hold,then GPFQIconverges in the batch sequential algorithm provided the data points are sufficiently dense in the domain:

Atevery iteration,GP-FQIw ill converge to a fixed estimate ofQ∗at the current data locations.Provided that the policy used for obtaining samples ensures ergodicity of the induced Markov chain,the algorithm w ill converge to an estimate ofQ∗everywhere.Ifwe use a non-sparse GPw ith infinite data,we add the condition that there iszero probability of sampling a finite set of data points infinitely often in order to prevent‖K(Z,Z)‖from grow ing to infinity.Additionally,if a sparse GP is used,then we know from Theorem 3 that our error is ultimately bounded.

A.Online GPQ

In theory,GP-FQIprovidesamethod w ith provable convergence,however the computational requirements can be intense.In our empirical results,we employ several approximations to GP-FQI to reduce the computational burden.We call this modified algorithm online GPQ and display it in A lgorithm 2.At each step of online GPQ,we take an action according to some policythat ensures ergodicity of the induced Markov chain,and observe the valueyτ=r+γmaxbτ(s′,b)at locationzτ.The sparse online GP algorithm of[14]is used to determine whether or not to add a new basis vector to the active bases setBVand then update the kernel weights.We provide a set of sufficient conditions for convergence in the online case.

Theorem 4.For an ergodic sample obtaining policy,and for each active basis set,a sufficient condition for conver£gence of(zt)→⁄m∗(zt)as£t→ ∞online GPQ⁄iswhere

Here,Ctis a negative definite andK−1tis a positive definitematrix related to the posterior and the prior covariance explained in[14].These sufficient conditions for convergence are less restrictive than[7]for Q-learning.The proof style follows closely to thatof[7].For details,the reader is referred to Appendix B.2.

It should be noted thatwhile the convergence results presented here are significant because no such results have been available before,these results only guarantee the asymptotic convergence of the Q-function to the approximate Bellman operator′s fixed point,w ithin the projection of the selected bases.Which means the algorithm w ill eventually converge,yet no guarantees on the rate of convergence are provided here.Such guaranteesare expected to depend on the choice of the exploration scheme,the algorithm′s eventual selection of bases,and the rate atwhich the predictive variance decreases.

B.Optimistic Exploration for GPQ

The online GPQ algorithm above used an†-greedy exploration strategy,which may not collect samples in an efficient manner.We now consideramore targeted exploration heuristic facilitated by the GP representation.Others have considered sim ilar heuristics based on information theory 6.Here we use a simpler strategy based on the“optim ism in the face of uncertainty”principle,which has been a cornerstone of efficient exploration algorithms(e.g.,[23]).

In the discrete-state case,optimistic value functions can bemaintained by initializing Q-values toRmax/(1− γ)and perform ing updates thatmaintain optim ism until the values are nearly accurate.Pairing this over-estimate w ith greedy action selection causes the agent to explore areas of the state space thatmay yield higher long-term values,but not at the expense of“known”areaswhich have higher valuesgrounded in real data.We propose using the upper confidence tails from the GP as an optimistic value function.Specifically,for any point〈s,a〉,the GP w ill report an upper confidence tail ofm(s)+2Σ(sτ+1)wheremandΣare defined in Section II-C.We modify GPQ to use these optimistic estimates in two ways:change value used in GP update to(si,ai)=r(si)+γmaxa[(si+1,a)+2Σ(s,a)],and always takeactions that are greedy w ith respect to the upper confidence tail.

The fi rst change uses the upper tail of the next state′s Q-value in the Bellman update to maintain optim ism of the value function and is rem iniscent of the backups performed in model-based interval estimation(38).The second change makes the algorithm select greedy actions w ith respect to an optim istic Q-function.

A degree of caution needs to be used when employing this optim istic strategy because of potentially slow convergence rates for GPQ when large amounts of data been collected.Once a large amount of data has been collected at a certain point,the confidence interval at that location can converge before GPQ has centered themean around the true Q-value.

These temporarily incorrect Q-values w ill still be optimistic and encourage exploration,but itmay take a large amount of time for these points to converge to their true values,meaning this technique is prone to over-exploration.However,inmany of our empirical tests,this variance-based exploration significantly outperformed†-greedy exploration.

V.RESULTS

Our experiments cover three domains,a discrete 5×5 Gridworld,a continuous state inverted pendulum(see(25)),and continuous state Puddle World[36].Specific details of the domains are listed in Appendix C.These domains pose increasingly more difficult challenges to GPQ when choosing basispoints.The algorithms compared in each domain include the two variants of online GPQ(†-greedy and optim istic),both using a budgeting scheme[14].We also implemented a tabular Q-learner(QL-tab)using discretization,Q-learning w ith fixed-basis linear function approximation(QL-FB),and the GQ algorithm[4].We chose these algorithms because they are off-policy and model-free online approaches for dealing w ith continuous state spaces.We report results for the best case parameter settings(see Appendix C)of 1)the learning rate(QL-tab,FA-FB,GQ),2)theexploration rate(QL-tab,FAFB,GQ,GPQ-†-greedy),3)bandw idth of kernel(FA-FB,GQ,GPQ),4)the position of kernels(GQ,FA-FB,GPQ)and 5)the numberof kernels(quantization level forQL-tab).After crossvalidation,the policy learned from all thesemethods for the three domains are evaluated based on discounted cumulative reward averaged over 20 independent runs and are shown in Fig.2.

The Gridworld consisted of 25 cells,noisy transitions,and a goal reward of 1(step reward of 0).While all of the algorithms find the optimal policy,the GPQ based methods convergemuch faster by quickly identifying important areas for basis points.We also see thatoptimistic exploration using the GP′s variance is advantageous,as the algorithm very quickly uncovers the optimal policy.

The inverted pendulum is a continuous 2-dimensional environmentw ith the reward defined as the difference between the absolute value of the angle for two consecutive states.Again,GPQ quickly finds adequate bases and converges to a near optimal policy while GQ requiresmore samples.Q-learning w ith fixed basesand a tabular representation achieve adequate policies as well but require thousands of more samples.Optimistic exploration isnotashelpful in thisdomain since the pendulum usually starts near the goal so targeted exploration is not required to find the goal region.Additional graphs in the appendix show thatoptim istic exploration is beneficial for certain parameter settings.The graphs in the appendix also demonstrate thatGPQmethodsaremore resilientagainstsmall quantizations(budgets)because they are able to select their own bases,while GPQ and QL-FB are farmore sensitive to the number and placement of bases.

Finally,we performed experiments in the PuddleWorld domain,a continuous 2-dimensional environmentw ith Gaussian transition noise and a high-costpuddle between the agentand the goal.Because of the large range of values around the puddle,basis placement ismore challenging here than in the other domains and GPQ sometimes converges to a cautious(puddle adverse)policy.Multiple lines are shown for QLFB and GQ,depicting their best and worst case in terms of parameter settings,as they were extremely sensitive to these settings in this domain.Note that the best case versions of GQ and QL-FB reached better policies than GPQ,in the worst case,their Q-values appear to diverge.While this is not immediately evident from the discounted-reward graph,an additional graph in the appendix shows the average steps to the goal,which more clearly illustrates this divergence.While GQ has convergence guarantees when data comes from a fixed policy,those conditions are violated here,hence the potential for divergence.In summary,while very careful selection of parameters for QL-FB and GQ leads to slightly better performance,GPQ performs almostaswellas their best case w ith less information(since it does not need the bases a priori)and far outperforms theirworst-case results.

V I.CONCLUSIONS

In this paper,we presented a nonparametric Bayesian framework(GPQ)that uses GPs to approximate the value function in off-policy RL.We presented algorithms using this framework in the batch and online case and provided sufficient conditions for their convergence.We also described exploration scheme for the online case thatmade use of the GP′s prediction confidence.Our empirical results show that GPQ′s representational power allows it to perform as wellor better than other off-policy RL algorithms.Our results from also reveal thata regularization-like term can help avoid in an application Thoerems 1∼3 of off-policy approximate reinforcement learning employing Gaussian kernels.In future work,we plan to analyze the theoretical properties of our optim istic exploration scheme and deploy the algorithm on practical robotics platforms.

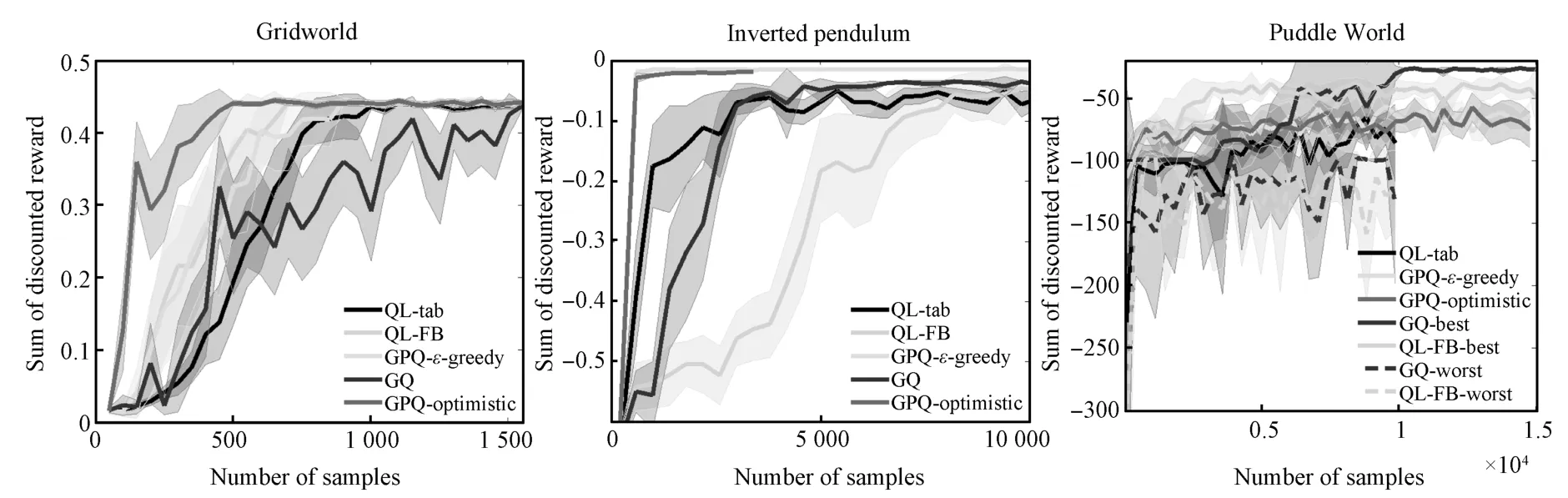
Fig.2 Average sum of discounted rewards for the experimental domains.The GQ and the QL variants are givenmore information because their bases are specified a priori,yet GPQ is able to reach comparable performance(often faster)while choosing its own basis functions.

APPENDIX A SEQUENTIAL GPUPDATES

Perform ing batch prediction using GPs requires the inversion of amatrix thatscalesw ith the size of the data.Inverting this matrix at every iteration is computationally taxing,and many sparsification schemes have been proposed to reduce this burden[14,31−32].In this paper,we use the sparsification method used in[14],which allows for sequential updates.The sparsification algorithm in[14]works by building a dictionary of basis points that adequately describe the input domain w ithout including a basis pointat the location of every observed data point.

Given a dictionary of bases,Zd,the prediction and covariance equations are computed as

whereC=−(K+ω2I)−1,i.e.,Cis the negative of the inverseof the regularized covariancematrix which is computed recursively.A natural and simple way to determine whether to add a new point to the subspace is to check how well it is approximated by the elements inZ.This is known as the kernel linear independence test[14],and has deep connections to reproducing kernel Hilbert spaces(RKHS)[5].The linear independence testmeasures the length of the basis vector(zτ+1)that is perpendicular to the linear subspace spanned by the current bases.For GPs,the linear independence test is computed as

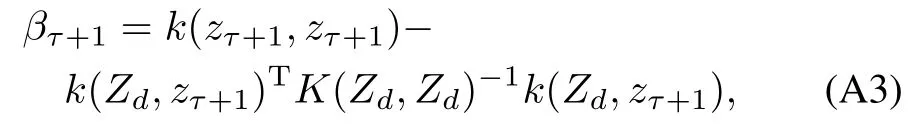
whenβτ+1is larger than a specified threshold†to l,then a new data point should be added to the dictionary.Otherw ise,the associated weightsατare updated,but the dimensionality ofατremains the same.When incorporating a new data point into the GPmodel,the inverse kernelmatrix and weights can be recomputed w ith a rank−1 update.To compute the updates in an online fashion,fi rst define the scalar quantities

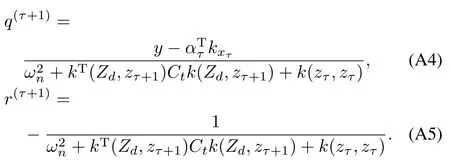
Leteτ+1be the(τ+1)coordinate vector,and letTτ+1(·)andUτ+1(·)denote operators that extend aτ-dimensional vector and matrix to a(τ+1)vector and(τ+1)×(τ+1)matrix by appending zeros to them,respectively.The GP parameters can be solved recursively by using

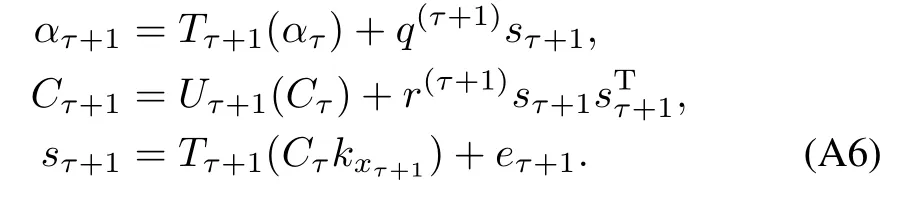
The inverse of thematrixK(Z,Z),denoted byP,needed to solve forγτ+1is updated online through

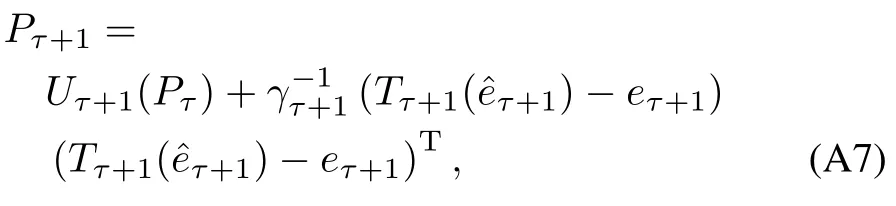
APPENDIX B CONVERGENCE PROOFS

A.Batch GP-TQE

Theorem 2.Given a GPw ith infinite data generated using a sparse approximation w ith acceptance toleranceβto l,and given a Mercer kernel function that decays exponentially,there exists a finite regularization parametersuch that the Bellman operatorTis a contraction in the batch setting.

Proof.We show that for a Mercer kernel that decays exponentially,there always exists a finitesuch that the Bellman operator results in a contraction in the supremum norm.For ease of exposition,allnorms are assumed to be the infinity norm unless otherw ise stated.Consider the Bellman operator

To bound‖K(Z,Z)‖‖(K(Z,Z)+I)−1‖ ≤1,fi rstconsider the norm of‖K(Z,Z)‖.By the structure of the kernel,we know

We now argue that the norm ofK(Z,Z)is bounded for an infinite number of basis vectors selected using the linear independence test in(A9).The number of points that can be included in the basis vector set given the sparse selection procedure grows only polynom ially as the volume of the input space increases.However,the kernel function decays exponentially fastas a function of distance.Therefore,as thevolume of the input domain increases,the number of added kernels increases polynom ially while the value they add to the sum(A10)decays exponentially fast.Thismeans that the sum is convergent as the number of BV goes to infinity.We formalize this notion.

The following argument assumes a squared exponential kernel function,M＞0.However,the results generalize to a variety of kernels that decay exponentially fast.Given some sparsity parameterβto l,thereexistsan associatedweighted distancesuch that all points.In particular,thisbound can be computed as=−ln(1−βto l).

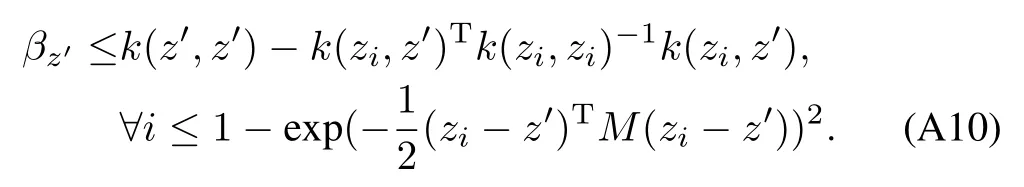
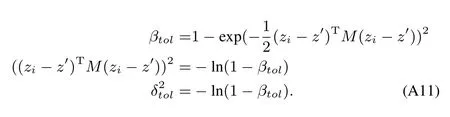
This gives us a bound on how close any two points can be in a sparse GP.We now assume the worst case analysis that all points are as compact as possible while satisfying(A11).Given a volume in the input domain,distributing a maximal number of basis vectors is equivalent to perform ing a patterning operation w ith a lattice.

From Ehrhart′s theory[39],we know that the number of lattice points in a polytope scales polynom ially w ith the axis scaling factor,t,w ithmaximum degree equal to the dimension of the space.In order to place an upper bound on(A9)to show convergence,we begin by considering the case of concentric hyperspheres of radiinδto l,n∈Z around a basis vector location.Each hypersphere contains a number of lattice points that grows polynom ially as some functionL(nδto l).To conservatively estimate,one can add the total number of lattice points contained in the interior of the hypersperen+1,L((n+1)δto l),at the distancenδto l.This estimate is conservative in two ways.First,all of the lattice points inside hyperspherenare counted multiple times in the summation.Secondly,all of the lattice points at a distance between[nδto l,(n+1)δto l]are given weight at distance(nδto l).Summing over allhyperspheres,we have for anyzj,

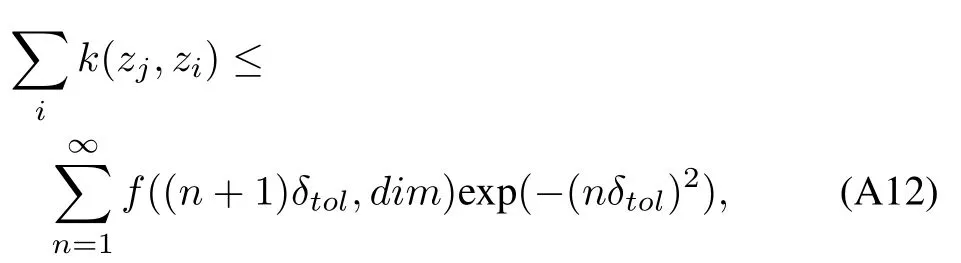
wheref((n+1)δto l,dim)exp(−(nδto l)2)is a polynom ial function w ith highest degree dim.Substituting

One can easily verify that the rightside of(A13)convergesby the integral test.Since‖K(Z,Z)‖is finite,we know that there exists a finitethat results in contraction for the Bellman operator.

B.Online GPQ

In the following,we present a sufficient condition for convergence of online GPQ(see Section IV-A).Themain idea is to show that themean of the GPestimate of the Q-function,,converges to themeanm∗.Note that,whereα∗is the unique m inim izer of the regularized least squarescost function.Foreaseof exposition,we define the follow ing notation:k(Zt,zt)=kkkt,.Similar to proofs of other online RL algorithms,including TD learning[18]and Q-learning[7],an ODE approach is used to establish stability[40].The update in(15)is rew ritten here for the case when the active basis set is fixed,that is,whenβt≤ βto l

Theorem 4.For an ergodic sample obtaining policyand for each active basis setBV,a sufficient condition for convergencew ith probability 1 of(zt)→m∗(zt)ast→ ∞when using the online sparse GP algorithm of(A14)w ith the measurementmodelin(3)of themain paper is

Proof.Ensuring that assumptions required for Theorem 17 of[40]hold,the follow ing ODE representation of theαupdate(A14)exists:

In the follow ing,it is shown thatα→ α∗for each active basis set.Letand consider the continuously differentiable function＞0 for all/=0,therefore,Vis a Lyapunov like candidatefunction[41−42].The fi rstderivative ofValong the trajectories ofα(t)is

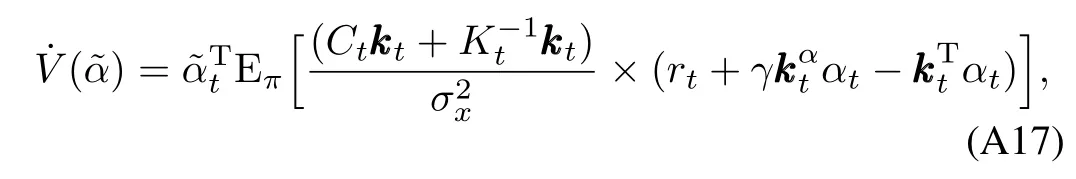
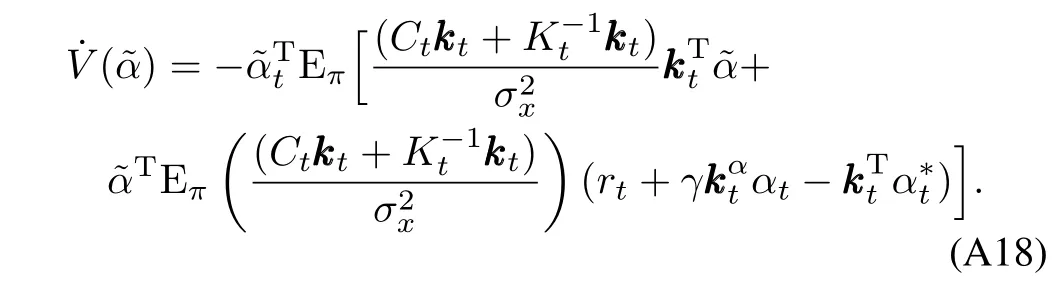
Hence,if the condition in(A15)is satisfied,()＜0 andα→α∗w ith probability 1 for each active basis set.

The argumentabove can be extended to show thatm(z)→m∗(z)even if new bases are added to the active basis set.To see this,letkbe the time instant when a new basis is added and letbe the associated ideal weight vector.

Note that the nature of the sparse GP algorithm ensures thatk+1≥k+ΔTw ithΔT＞0.IfΔTis sufficiently large such thatthen the convergence is uniform across all bases.

APPENDIX C DETA ILSOF EMPIRICAL RESULTS

Our experiments cover three domains,discrete 5×5 Gridworld,a continuous state inverted pendulum(similar to[43]),and continuous state Puddle World[36].The Gridworld consisted of 25 cellswith the agent always starting in the lowerleft corner,a 0 step cost,and a goal state in the upper-right cornerw ith reward 1 andγ=0.9.Transitionswere noisy w ith a 0.1 probability of the agent staying in its current location.We also performed experiments on the inverted pendulum,a continuous 2-dimensional environment w ith three actions:applying forces of−50N,0N,or 50.The goal is to balance the pendulum uprightw ithin a threshold of(−/2,/2)and the reward is defined as the difference between the absolute value of the angle for two consecutive states.

The PuddleWorld domain isa continuous2-dimensionalenvironmentw ith an agentmoving in the four compassdirections and Gaussian noise added to itsmovements.The initialstate is at the bottom leftof the domain and the goal region isnear the top-rightcorner.Thegoal region and puddle placement follows the description of[36].The“puddle”(which is really two overlapping puddles)between the agent and the goal causes negative reward proportional to the agent′s distance to the center of each puddle.Steps outside of the puddle cause a reward of−1 except at the goalwhere the reward is 0.

The results are influenced by several parameters,including 1)the learning rate(QL-tab,FA-FB,GQ),2)the exploration rate(QL-tab,FA-FB,GQ,GPQ-†-greedy),3)bandw idth of kernel(FA-FB,GQ,GPQ),4)the position of kernels(GQ,FA-FB,GPQ)and 5)the number of kernels(quantization level for QL-tab).The learning rate is set as 0.5/tαw ithα∈{0.1,0.3,0.5},the exploration rate is set according to 1/tβw ithβ∈{0.1,0.3,0.5}.For Gridworld the kernel budget is 25;for Inverted Pendulum,the budget is chosen from{36,100}and for Puddle World we use budgets from{100,400}.The quantization level for tabular Q-Learning is set the same as the budget for those function approximation methods.For each of the algorithms,the best combination of parameter settingswas used for the figures in themain paper.

The follow ing experiments from the inverted pendulum domain show the robustness of GPQ against changes in the quantization(budgeting)level and also the sensitivity of the fixed basis methods to the number of basis points.Fig.A2 demonstrates that GPQ methods are more resilient against small budgets because they are able to select their own bases,while GPQ and QL-FB are far more volatile.These graphs also show that optim istic exploration is beneficial for certain parameter settings.

Fig.A1.The performance of GPQ w ith†-greedy exploration on Baird′s counterexample(the“Star”problem)which can cause divergencew ith fixed-basis linear function approximation.

The graphs evaluating performance in Puddle World in Fig.A3 include an additional graph that shows the average steps to the goal,whichmore clearly illustrates the divergence of GQ and QL-FB.The divergence in these worst cases is caused by having many bases(＞100)w ith overlapping bandw idths(＞0.05).In contrast,a smaller number of bases w ith the same small bandw idth actually produces the bestperformances for these algorithms,because weights are updated almost independently.Fig.A4 elaborates on this sensitivity by show ing the performance of all the algorithm under different budget(quantization)constraints w ith all other parameters fixed.We see GQ and QL-FB are very sensitive to the budget,and QL-tab is sensitive to the quantization level,while GPQ is relatively stable.In summary,while very careful selection of parameters for QL-FB and GQ leads to slightly better performance,GPQ performs almost aswell as their best case w ith less information(since itdoesnotneed thebasesa priori)and far outperforms theirworst-case results.

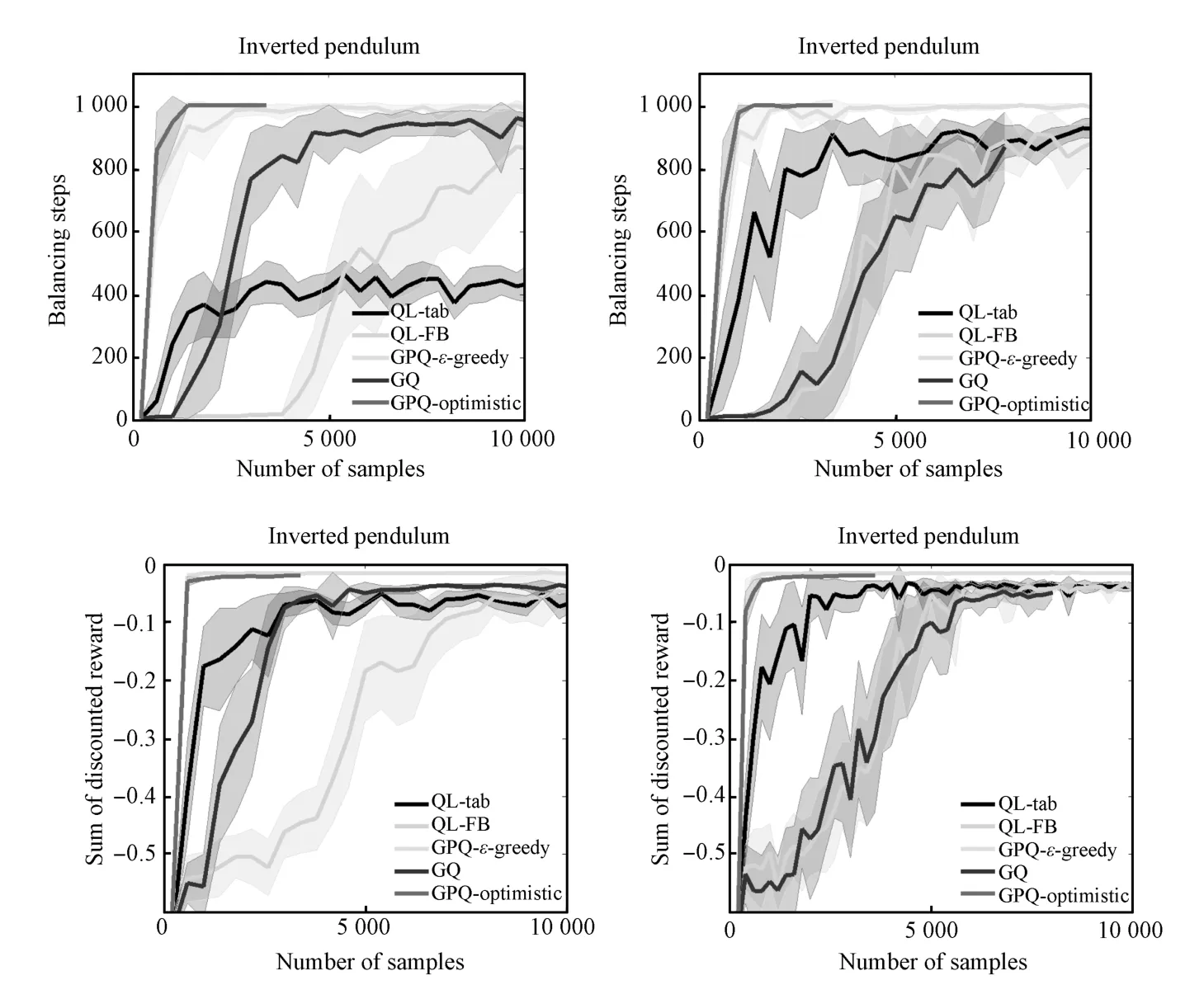
Fig.A2.The performance for inverted pendulum under differentbudget(quantization levels),36(left)and 100(right).GPQ is not sensitive to the quantization level because itselects its own bases,while the quantization level impacts the other algorithms significantly.For example,w ith higher a quantization level GQ converges slow ly,and w ith a lower quantization level QL-tab performances poorly.

Fig.A3.The performance of the algorithms in Puddle World.The bandw idth is set to be 0.1 for the basis function in allmethods.The number of basis(budget)is set to be 400.FA-FB and GQ diverge when the bases are placed uniform ly over the state space.

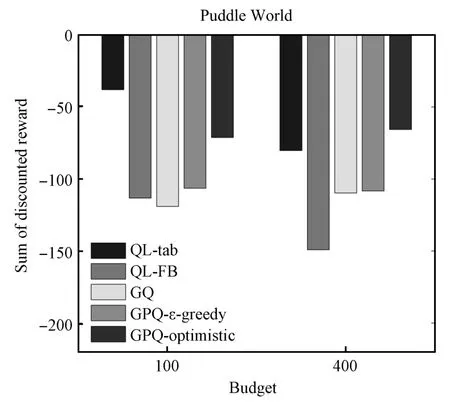
Fig.A4.The performance for PuddleWorld under different budget(quantization levels).

[1]Sutton R,Barto A.ReinforcementLearning,an Introduction.Cambridge,MA:M IT Press,1998.

[2]Engel Y,Mannor S,Meir R.Reinforcement learning w ith Gaussian processes.In:Proceedings of the 22nd International Conference on Machine learning.New York:ACM,2005.201−208

[3]Ernst D,Geurts P,Wehenkel L.Tree-based batch mode reinforcement learning.JournalofMachine Learning Research,2005,6:503−556

[4]Maei H R,Szepesv´ari C,Bhatnagar S,Sutton R S.Toward off-policy learning control w ith function approximation.In:Proceedings of the 2010 InternationalConferenceon Machine Learning,Haifa,Israel,2010.

[5]Rasmussen C E,Williams C K I.Gaussian Processes for Machine Learning.Cambridge,MA:The M IT Press,2006.

[6]Engel Y,Szabo P,Volkinshtein D.Learning to control an octopus arm w ith gaussian process temporal difference methods.In:Advances in Neural Information Processing Systems 18.2005.347−354

[7]Melo FS,Meyn SP,Ribeiro M I.An analysisof reinforcement learning w ith function approximation.In:Proceedings of the 2008 International Conference on Machine Learning.New York:ACM,2008.664−671

[8]Deisenroth M P.Efficient Reinforcement Learning Using Gaussian Processes[Ph.D.dissertation],Karlsruhe Institute of Technology,Germany,2010.

[9]Jung T,Stone P.Gaussian processes for sample efficient reinforcement learning w ith rmax-like exploration.In:Proceedings of the 2012 European Conference on Machine Learning(ECML).2012.601−616

[10]Rasmussen C,KussM.Gaussian processes in reinforcement learning.In:Proceedingsof the Advances in Neural Information Processing Systems,2004,751−759

[11]Kolter J Z,Ng A Y.Regularization and feature selection in leastsquares temporaldifference learning.In:Proceedingsof the 26th Annual International Conference on Machine Learning.New York:ACM,2009.521−528

[12]Liu B,Mahadevan S,Liu J.Regularized off-policy TD-learning.In:Proceddings of the Advances in Neural Information Processing Systems 25.Cambridge,MA:The M IT Press,2012.845−853

[13]Sutton R S,Maei H R,Precup D,Bhatnagar S,Silver D,Szepesv´ari C,Wiew iora E.Fast gradient-descentmethods for temporal-difference learning with linear function approximation.In:Proceedingsof the 26th Annual InternationalConferenceon Machine Learning.New York,USA:ACM,2009.993−1000

[14]Csat´o L,Opper M.Sparse on-line gaussian processes.Neural Computation,2002,14(3):641−668

[15]Singh S P,Yee R C.An upper bound on the loss from approximate optimal-value functions.Machine Learning,1994,16(3):227−233

[16]Watkins C J.Q-learning.Machine Learning,1992,8(3):279−292

[17]Baird L C.Residual algorithms:reinforcement learning w ith function approximation.In:Proceedings of the 12th International Conference on Machine Learning.Morgan Kaufmann,1995.30−37

[18]Tsitsiklis JN,van Roy B.An analysis of temporal difference learning w ith function approximation.IEEE Transactions on Automatic Control,1997,42(5):674−690

[19]Parr R,Painter-Wakefield C,Li L,Littman M L.Analyzing feature generation forvalue-function approximation.In:Proceedingsof the2007 International Conference on Machine Learning.New York:IEEE,2007.737−744

[20]Ormoneit D,Sen S.Kernel-based reinforcement learning.Machine Learning,2002,49(2−3):161−178

[21]Farahmand A M,Ghavamzadeh M,Szepesv´ari C,Mannor S.Regularized fi tted q-iteration for planning in continuous-space Markovian decision problems.In:Proceedings of the 2009 American Control Conference.St.Louis,MO:IEEE,2009.725−730

[22]GeistM,Pietquin O.Kalman temporal differences.JournalofArtificial Intelligence Research(JAIR),2010,39(1):483−532

[23]Strehl A L,Littman M L.A theoreticalanalysis ofmodel-based interval estimation.In:Proceedings of the 22nd International Conference on Machine Learning.New York:IEEE,2005.856−863

[24]Krause A,Guestrin C.Nonmyopic active learning of Gaussian processes:an exploration-exploitation approach.In:Proceedings of the 24th International Conference on Machine Learning.New York:IEEE,2007.449−456

[25]Desautels T,Krause A,Burdick J W.Parallelizing explorationexploitation tradeoffs w ith Gaussian process bandit optimization.In:Proceedings of the 29th International Conference on Machine Learning.ICML,2012.1191−1198

[26]Chung J J,Law rance N R J,Sukkarieh S.Gaussian processes for informative exploration in reinforcement learning.In:Proceedings of the 2013 IEEE International Conference on Robotics and Automation.Karlsruhe:IEEE,2013.2633−2639

[27]Barreto A D M S,Precup D,Pineau J.Reinforcement learning using kernel-based stochastic factorization.In:Proceedingsof the Advances in Neural Information Processing Systems 24.Cambridge,MA:The M IT Press,2011.720−728

[28]Chen X G,Gao Y,Wang R L.Online selective kernel-based temporal difference learning.IEEETransactionson NeuralNetworksand Learning Systems,2013,24(12):1944−1956

[29]Kveton B,Theocharous G.Kernel-based reinforcement learning on representative states.In:Proceedings of the 26th AAAIConference on Artifi cial Intelligence.AAAI,2012.977−983

[30]Xu X,Hu DW,Lu X C.Kernel-based least squares policy iteration for reinforcement learning.IEEE Transactions on Neural Networks,2007,18(4):973−992

[31]Snelson E,Ghahramani Z.Sparse Gaussian processes using pseudoinputs.In:Proceedings of the Advances in Neural Information Processing Systems.Cambridge,MA:M IT Press,2006.1257−126

[32]L´azaro-Gredilla M,Qui´nonero-Candela J,Rasmussen C E,Figueiras-Vidal A R.Sparse spectrum gaussian process regression.The Journalof Machine Learning Research,2010,11:1865−1881

[33]Varah JM.A lower bound for the smallest singular value of amatrix.LinearA lgebraand Its Applications,1975,11(1):3−5

[34]Lizotte D J.Convergent fi tted value iteration w ith linear function approximation.In:Proceedings of the Advances in Neural Information Processing Systems 24.Cambridge,MA:The M IT Press,2011.2537−2545

[35]Kingravi H.Reduced-Set Models for Improving the Training and Execution Speed of Kernel Methods[Ph.D dissertation],Georgia Institute of Technology,Atlanta,GA,2013

[36]Boyan J,Moore A.Generalization in reinforcement learning:Safely approximating the value function.In:Proceedings of the Advances in Neural Information Processing Systems 7.Cambridge,MA:The M IT Press,1995.369−376

[37]Engel Y,Mannor S,Meir R.The kernel recursive least-squares algorithm.IEEETransactionson SignalProcessing,2004,52(8):2275−2285

[38]Krause A,Singh A,Guestrin C.Near-optimal sensor placements in gaussian processes:theory,effi cient algorithms and empirical studies.The JournalofMachine Learning Research,2008,9:235−284

[39]Ehrhart E.Geometrie diophantienne-sur les polyedres rationnels homothetiques an dimensions.Comptesrendushebdomadairesdesseancesde l′academ ia dessciences,1962,254(4):616

[40]Benveniste A,PriouretP,M´etivier M.Adaptive A lgorithmsand Stochastic Approximations.New York:Springer-Verlag,1990

[41]Haddad W M,Chellaboina V.Nonlinear Dynam ical Systems and Control:A Lyapunov-Based Approach.Princeton:Princeton University Press,2008

[42]Khalil H K.NonlinearSystems.New York:Macm illan,2002.

[43]Lagoudakis M G,Parr R.Least-squares policy iteration.Journal of Machine Learning Research(JMLR),2003,4:1107−1149