Event-Triggered Optimal Adaptive Control Algorithm for Continuous-Time Nonlinear Systems

Kyriakos G.Vamvoudakis

I.INTRODUCTION

O PTIMAL feedback control design has been responsible for much of the successful performance of engineered systems in aerospace,industrial processes,vehicles,ships,and robotics.But the vastmajority of the feedback controllers use digital computers,and rely on periodic sampling,computation,and actuation.Shared congestion and energy saving objectives demand that every information through a network should be rigorously decided when to transmit.For that reason oneneeds to design“bandw idth”effective controllers thatcan function in event-driven environments and update their values only when needed.Event-triggered control design is a new ly developed framework that can potentially have lots of applications that have lim ited resources and controller bandw idth and offers a new point of view,w ith respect to conventional time-driven strategies,on how information could be sampled for control purposes.

The event-triggered controlalgorithms(see[1-3])are composed of a feedback controller updated based on sampled state,and the event-triggering mechanism that determines when the control signal has to be transm itted from a stability and performance point of view.This can reduce the computation and communication resources significantly.For linear systems,sampled-data control theory provides powerful tools for direct digital design,while implementations of nonlinear control designs tend to rely on discretization combined w ith fast periodic sampling.The basic idea is to communicate,compute,or control only when something significant has occurred in the system.Themotivation for abandoning the timetriggered paradigm is to better cope w ith various constraints or bottlenecks in the system,such as sensors w ith lim ited resolution,lim ited communication or computation bandw idth,energy constraints,or constraintson the numberof actuations.In order for the controller to keep the previous used state sample,a sampled-data and a zero-order-hold(ZOH)actuator component are commonly used.

All the event-triggered control algorithms available in the literature rely on a combination of offl ine computations,in the sense of computing the Riccati or Hamilton-Jacobi-Bellman equations,and online computations in the sense of updating the controller.Computing and updating controller parameters using online solutionsmay allow for changing dynam ics,e.g.,to handle the reduced weight of an aircraft as the fuel burns.A ll this work has been mostly done for linear systems.For nonlinear systems things are more complicated because of the infeasibility of the Ham ilton-Jacobi-Bellman equation.For that reason,one needs to combine event-triggered controllers w ith computational intelligent ideas to solve the complicated Hamilton-Jacobi-Bellman equation online by updating the controller only when it isneeded butstillguaranteeing optimal performance of the originalsystem and nota linearized version of it.To overcome all those limitations we w ill use a reinforcement learning technique and specifically an actor/critic neural network framework[4].The actor neural network w ill eventually approximate the event-triggered optimal controller and the critic neural network w ill approximate the optimal cost.But since the dynam ics are evolving in both discrete time and continuous time we w illmodel it as an impulsive model[5−7].The discrete time dynam ics w ill take care of the“jumps”of the controller when an event is triggered and the continuous time dynamics w ill take care of the“inter-event”instants of the state,and the actor/critic neural networks.

There are several triggering conditions proposed in the literature mostly static state-feedback controllers(e.g.,[1-3],and the references therein)and output based controllers as in[8].In most of them,the event is triggered when the error between the last event occurrence and the current observation of the plant exceeds a bound.The authors in[9]proposed a networked event-based controlscheme for linear and nonlinear systems under non-ideal communication conditions,namely w ith packet drop outs and transmission delays.A framework for event-triggered controller communications in a network of multi-agents is proposed by[10]to solve a synchronization problem of linear agents.A problem w ith network delays and packet losses is being considered in[11],where the authors extented the regular event-triggered controller to cope w ith delays and losses in the feedback signal.In[12],the authors propose two types of optimal event-based control designunder lossy communication.Despite of their computational benefi ts compared to the optimal solution,it turns out that both algorithmsapproach the optimalsolution very closely but their algorithm relies heavily on offl ine optim ization schemes.By follow ing the work of[2−3],[13]combined modelbased network control and event-triggered control to design a framework for stabilization of uncertain dynamical systems subject to quantization and time-varying network delays.In[1],three different approaches are considered for periodic event-triggered control for linear systems,an impulsive approach,a discrete-time piecew ise linear system approach and a perturbed linear system approach.But all this is done for linear systemsby solving differential Riccatiequationsoffl ine.

The contributions of the present paper are fourfold.First,it is the fi rst time that an event-triggered controller for a nonlinearsystem issolved onlinew ith guaranteed performance and w ithout any linearizing process.Second,an actor/critic algorithm is used to approximate the cost and the eventtriggered controller by using neural networksw ith continuous and jump dynam ics.Those dynam icsaremodeled as impulsive systems.Third,we avoid using a zero-order hold component explicitly in the implementation of our algorithm,but rather implement it inside theactorneuralnetwork.Finally,the paper provides stability and optimal performance guarantees.

The remainder of the paper is structured as follows.Section IIformulates theproblem.In Section III,wepropose theonline event-triggered optimal adaptive control algorithm by using an actor/critic reinforcement learning framework.Simulation results and comparisons to a time-triggered controller for a linear and a nonlinear system are presented in Section IV.Finally,Section V concludes and talks about future work.

Notation.R denotes the real numbers set,R+denotes the set{x∈R:x＞0},Rn1×n2is the set ofn1×n2real matrices,N＞0 is the setof naturalnumbers excluding zero,‖·‖denotes the Euclidean norm,‖·‖Pdenotes the weighted Euclidean norm w ithPa matrix of appropriate dimens¡ions¢,and(·)Tdenotes the transpose.Moreover,we¡w rit¢efor them inimum eigenvalue ofmatrixMandMfor the maximum.Finally a continuous functionα:[0,α)→[0,∞)is said to belong to classKfunctions if it is strictly increasing andα(0)=0.

II.PROBLEM FORMULATION

Consider the follow ing nonlinear continuous-time system:

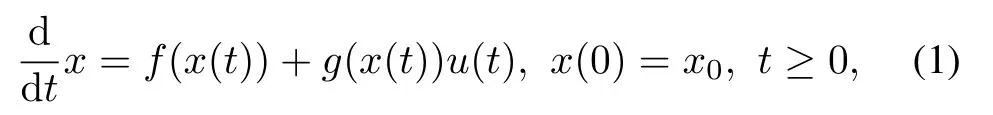
wherex∈Rnis a measurable state vector,f(x)∈Rn,is the drift dynamics,g(x)∈Rn×mis the input dynamics andu∈Rmis the control input.It is assumed thatf(0)=0 andf(x)+g(x)uis locally Lipschitz and that the system is stabilizable.

In order to save resources the controller w ill work w ith a sampled version of the state.For that reason one needs to introduce a sampled-data component that is characterized by a monotone increasing sequence of sampling instants(broadcast release times),whererjis thej-th consecutive sampling instant.The output of the sampled-data component is a sequence of sampled statesj,wherej=x(rj)for allandj∈N.The controller maps the sampled state onto a control vectorj,which after using a ZOH becomes a continuous-time input signal.For simplicity,we w ill assume that the sampled-data systems have zero task delays.An event triggered controlsystem architecture isshown in Fig.1.

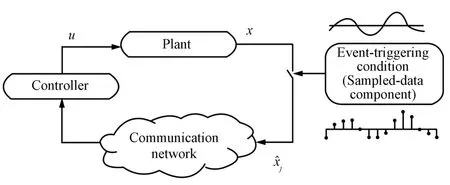
Fig.1. Event trigger control schematic.

In order to decidewhen an event is triggered wew ill define the gap or difference between the current statex(t)and the sampled statej(t)as

and the dynam ics of the gap are evolving according to

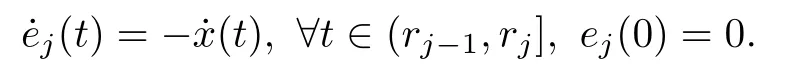
Remark 1.Note thatwhen an event is triggered att=rj,a new statemeasurement is rendered that resets the gapejto zero.

We want to find a controlleruof the formu=k(j(t))≡k(x(t)+ej(t))thatminim izes a cost functional sim ilar to the one w ith the time-triggered controller

w ith monotonically increasing functionQ(x)≥0 on Rnand w ith lim ited updates.

By using the error defined in(2),the closed loop dynam ics w ithu(j)=k(j(t))during the interval(rj−1,rj]can be w ritten as

to achieve input-to-state stability(ISS)w ith respect to the measurement errorsej(see(2)).The follow ing definition adopted from[3]is needed.n

Definition 1.A smooth positivedefinite functionV:R→R+is said to be ISS Lyapunov function for the closed-loop dynam ics(4)if there exist classK∞functions,αandγsatisfying

From this point of view,it is clear that in order for the closed-loop dynam ics(4)to be ISS w ith respect to the measurement errorsejthen there exists an ISS Lyapunov function for(4).

We shall see that the restrictive assumption on ISS is not needed in our proposed algorithm.

The ultimate goal is to find the optimal cost functionV∗defined by

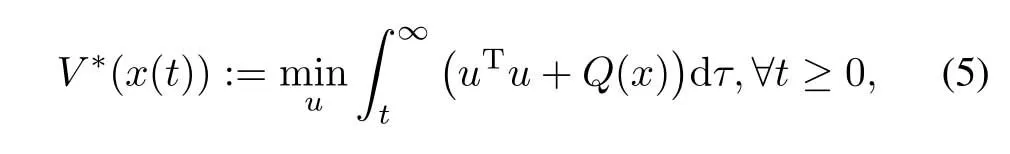
subject to the constraint(1)given an aperiodic event-triggered controller asw ill be defined in the subsequent analysis.

III.EVENT-TRIGGERED REGULATOR AND EX ISTENCE OF SOLUTION

One can define the Hamiltonian associated w ith(1)and(5)for the time-triggered case as

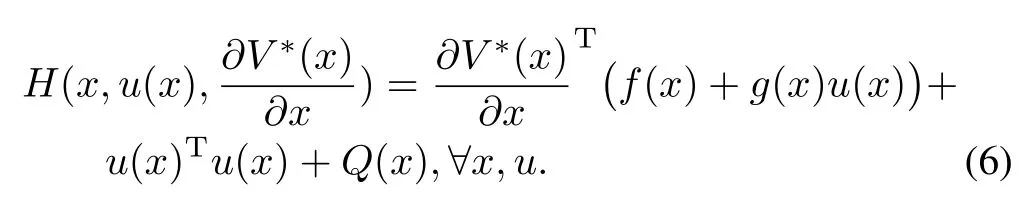
Now assume that the controller has unlim ited bandw idth.Then one needs to find the control inputu(t)such that the cost function(3)is m inim ized.Hence,we w ill employ the stationarity condition[14]into the Ham iltonian equation(6)and we w ill have

or

for the time-triggered case.

The optimal costand the optimal control satisfy the following Ham ilton-Jacobi-Bellman(HJB)equation,

From now on,we w ill call the HJB(8)as time-triggered HJB equation.

In order to reduce the communication between the controller and the plant,one needs to use an event-triggered version of the above HJB equation(8)by introducing a sampleddata componentw ith aperiodic controller updates that ensure a certain condition on the state of the plant to guarantee stability and performance as we w ill see in the subsequent analysis.For that reason the control input uses the sampledstate information instead of the trueoneand hence(7)becomes

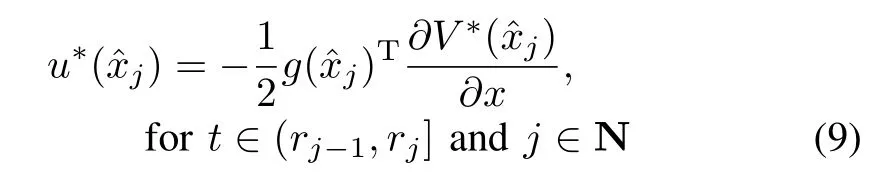
By using the event-triggered controller given by(9),the HJB equation(8)becomes∀x,j∈Rn,

which is eventually the equation we would like to quantify and compare it to(8).

The follow ing assumptions[2]are needed before we state the existence of solution and stability theorem for the eventtriggered control system.

Assumption 1.Lipschitz continuity of the controller w ith respect to the gapej,

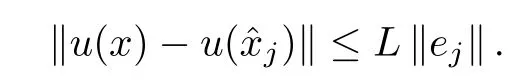
Assumption 2.Lipschitz continuity of the closed-loop system w ith respect to the state and to the gapej,

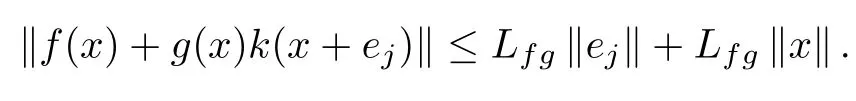
Remark 2.These assumptions are satisfied inmany applications where the controller is affine w ith respect toej.

Note that the control signalu∈R→Rmis a piecew ise constant function(produced by a ZOH w ithout any delay).The sequence of control can be w ritten as

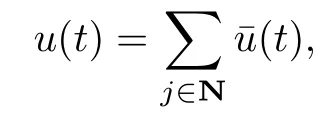
w ith,

Lemma 1.Suppose that Assumption 1 holds.Then the event-triggered HJB given by(10)can be related to timetriggered HJB given by(8)as

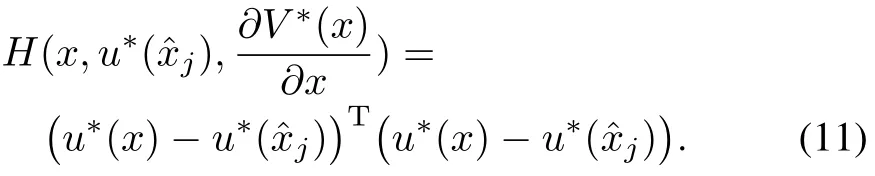
Proof.In order to prove the equivalence,we w ill take the difference between(8)and(10)as follows:

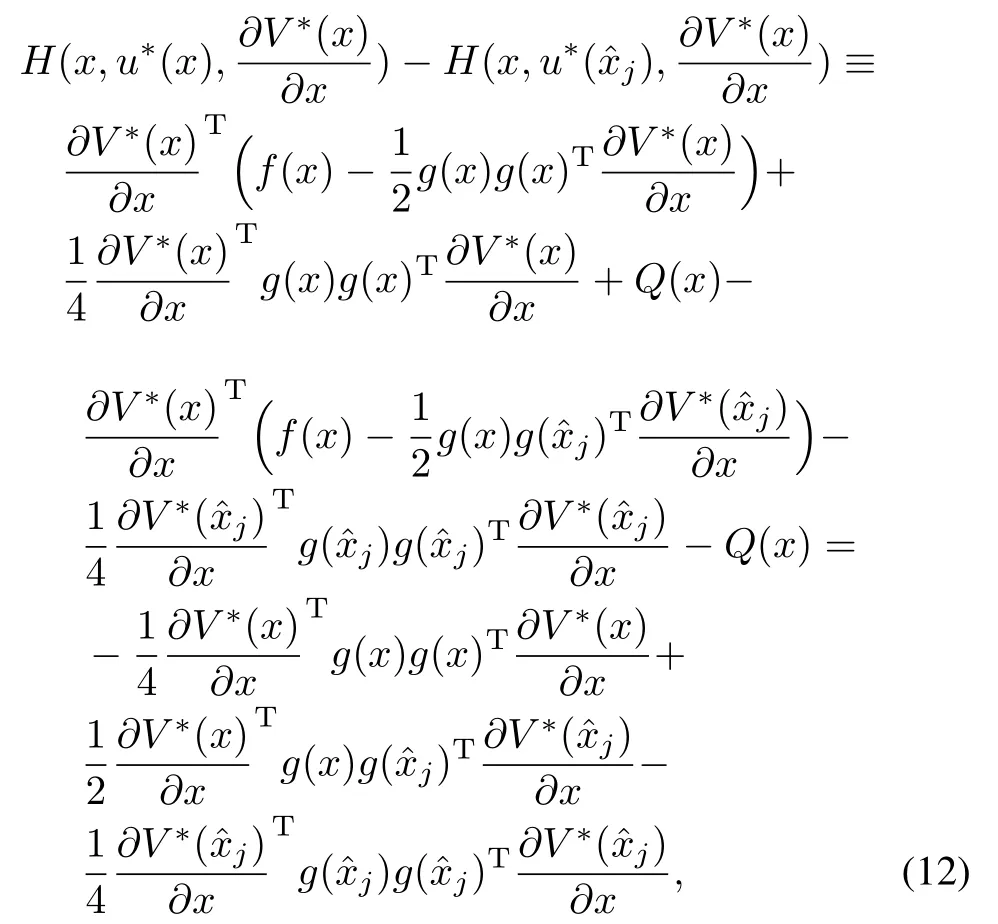
Remark 3.A fter taking norms and using Assumption 1 yields,

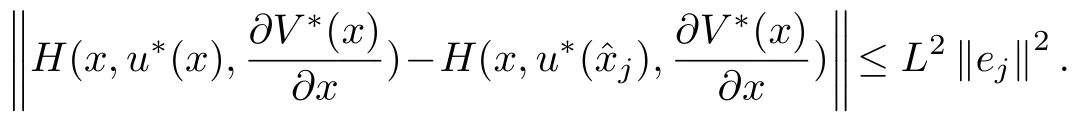
Now since¡ the¢ contro¡ller¢ is ISS then the state dependent thresholdmeans that at the broadcast timeejis forced to be zero.As the state asymptotically approaches the origin the threshold gets smaller.Furthermore,V∗from Definition 1 is an ISS-Lyapunov function for the continuously sampled(time-triggered)system.It is straightforward thatu∗(x)is a discretized version ofu∗(j).

Remark 4.We shall see in Theorem 1 thatwew ill pickejto guarantee optimality and stability.

The follow ing lemma adopted from[3]proves that the interexecution times are bounded.

Lemm a 2.For any compact setS⊆Rncontaining the origin,there exists a timeτ∈R+such that for any initial condition originating fromSthe inter execution release times{rj−rj−1}j∈Ndefined implicitly by(19)are lower bounded asτ≤rj−rj−1for allj∈N.See[3]for the proof.

Theorem 1.Suppose thereexistsa positive definite functionV∈C1thatsatisfies the time-triggered HJB equation(8)w ithV(0)=0.The closed-loop system fort∈(rj−1,rj],and allj∈N w ith control policy given by

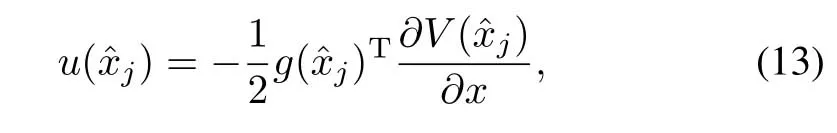
and triggering condition

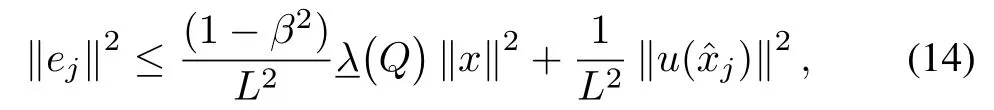
for some user defined parameterβ∈(0,1)is asymptotically stable.Moreover the control policy(13)is optimal and the optimal value is given by

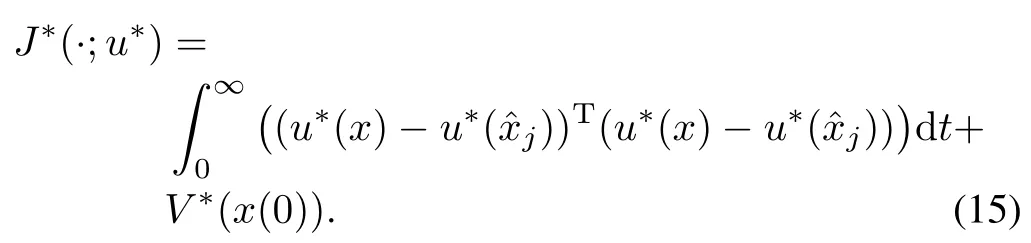
Proof.The orbital derivative along the solution of(1)w ith the event-triggered controller∀t∈(rj−1,rj]is

Now,by w riting the time-triggered HJB equation(8)as

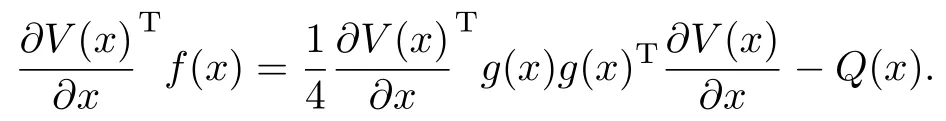
We can rew rite the orbital derivative(16)w ith the eventtriggered controller as

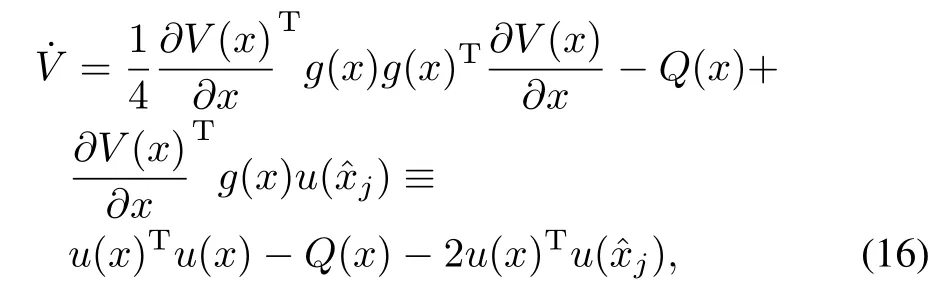
By using the Lipschitz condition from Assumption 1,we can w rite

Finally by substituting(18)into(17),and assum ing thatQ(x):=xTQxw ithQ∈Rn×n≥0,one has the follow ing bound:

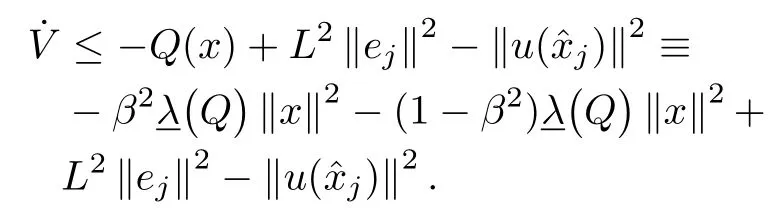
Finally the closed-loop system is asymptotically stable given that the follow ing inequality is satisfied for allt∈(rj−1,rj],

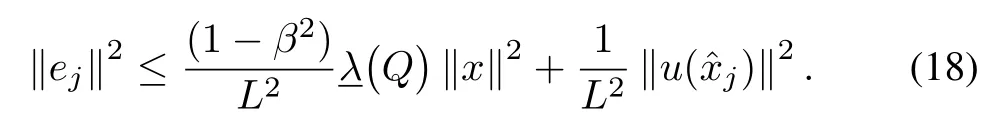
Now we need to show that the inter-transm ission time is nontrivial.Fort∈(rj−1,rj]and by using the Lipschitz continuity of the closed-loop dynamics according to Assumption 1,it has been shown in[2]that

wherewe used the fact that the ratio of the gap and the system statemust be greater than a positive constant

Since the functionVis smooth,zero at zero and converge to zero ast→∞and by denoting asV∗the optimal costwe can w rite(3)as

Now after subtracting zero from(11)and completing the squares yields

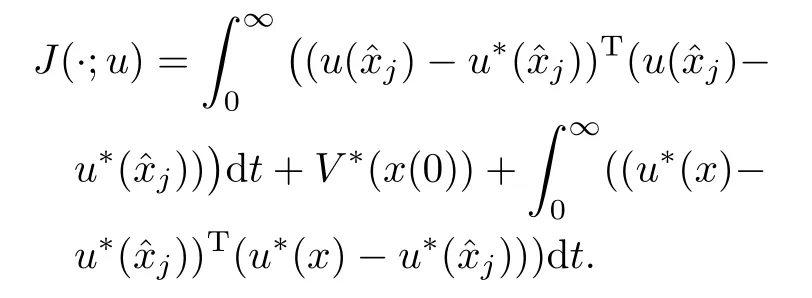
Now by settingu(j)=u∗(j),it is easy to prove that

where for brevity we have omitted the dependence on the initial conditions.

Remark 5.It is worth noting that if one needs to approach the performance of the time-triggered∫ con¡troller we need to make the quanti¢zation error termdtas close to zero as possible by adjusting the parameterβof the triggering condition given in(14).Thismeans thatwhenβis close to 1 one samplesmorefrequently whereaswhenβis close to zero,the intersampling periods become longer and the performance w ill be far from the time-triggered optimal controller.

Remark 6.The control law(13)iswell-defined and satisfies the usual optimality conditionJ∗(x(0);u∗)≤J(x(0);u)as discussed in[15].

Remark 7.The state sampler w ill continuously monitor the condition(14)and when a violation is about to occur the sampler w ill trigger the sampling of the system state.

In linear systems of the form=Ax+Buw ithA,Bmatricesof appropriate dimensions the previous theorem takes the follow ing form.

Corollary 1.Suppose there exists a positive definite function of the formV=xTPxwhereP∈Rn×nis a symmetric positive definitematrix that satisfies the follow ing Riccati equation:

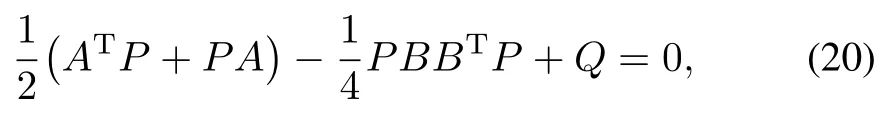
whereQ∈Rn×n≥0.The closed-loop system fort∈(rj−1,rj],and allj∈N w ith control policy given by

and triggering condition given by(14)isasymptotically stable.Moreover the control policy(22)is optimal,and the value is

Proof.The proof follows from Theorem 1 by direct substitutions.

Remark 8.Note thataccording to[2]one can use a simpler condition than(14),namelyfor some user defined parametersβ,δ∈(0,1).

A visualization of how the value(15)changesw ith the size of bandw idth is presented in Fig.2,where one can see that as the bandw idth increases by tweakingβto be close to 1,one approaches asymptotically the performance of the infinite bandw idth or time-triggered controller.

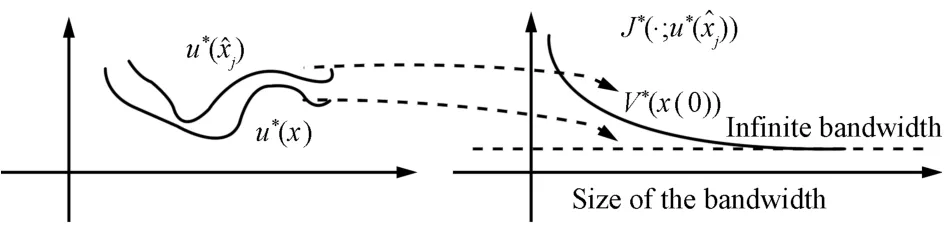
Fig.2. Visualization of the performance of the event-triggered control w ith respect to the time-triggered control and increased bandw idth.

Solving the event-triggered HJB equation(10)for the optimal cost for nonlinear systems and the Riccati equation(21)for the matrixPfor linear systems is in most of the cases infeasibleand has to be done in an offl inemanner thatdoesnot allow the system to change its objective while operating.For that reason the follow ing section w ill provide an actor/critic neural network framework to approximate the solution of the discretely sampled state controller HJB and Riccatiequations.

IV.ACTOR/CRITIC ALGORITHM

The fi rststep to solve theevent-triggered HJB equation(10)is to approximate the value functionV∗(x)from(5).Thevalue function can be represented in a compact setΩ⊆Rnby a critic neural network of the form

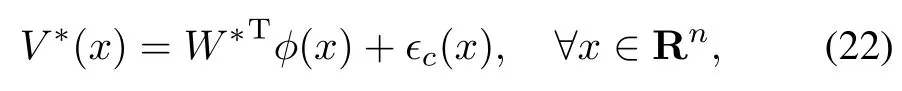
whereW∗∈Rhdenotes the ideal weights bounded as‖W∗‖≤Wmax,andis a bounded continuously differentiable basis function(‖φ‖ ≤φmaxandthe activation functions w ithhneurons,and†c(x)is the correspondin g res idual error such that supand supThe activation functionsφare selected such thath→∞one has a complete independent basis forV∗.

For causality issues and due to the online nature of our algorithm,wew ill define the triggering inter execution release time to be int∈(rj−1,rj]w ithj∈N(in the subsequent analysis,jw ill be in this set).

Based on this,the optimal event-triggered controller in(13)can be re-w ritten as

Remark 9.The control input jumpsat the triggering instants and remains constant∀t∈(rj−1,rj].This is in generally achieved w ith zero-order hold but we shall see that in our algorithm it is not necessary.

A.Learning Algorithm

The optimal event-triggered controller(24)can be approximated by another neuralnetwork which we callan actor.This has the follow ing form for allt∈(rj−1,rj]:

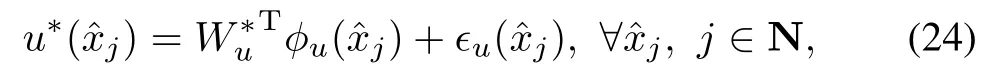
whereW∗u∈Rh2×mare the optimalweights andφu(ˆxj)are the NN activation functions defined sim ilarly to the critic NN andh2is the number of neurons in the hidden layer and†uis the actor approximation error.Note that in order foru∗to be uniform ly approximated the activation functions must define a complete independent basis set.The residual error†uand the activation functions are assumed to be upper bounded by positive constants as supand,respectively.

The value function(23)and the optimal policy(25)using currentestimatescandurespectively of the idealweightsW∗andW∗uare given by the follow ing critic and actor neural networks,

Ourgoalnow should be to find the tuning laws for theweightsandu.In order to do thatwe w ill use adaptive controltechniques[16].For that reasonwew illdefine the errorec∈R as

Hence one needs to pick the weightscto m inimize an integral squared error of the formas

whereαdetermines the speed of convergence.

By defining the critic error dynamics asc:=W∗−cand taking the time derivative one has

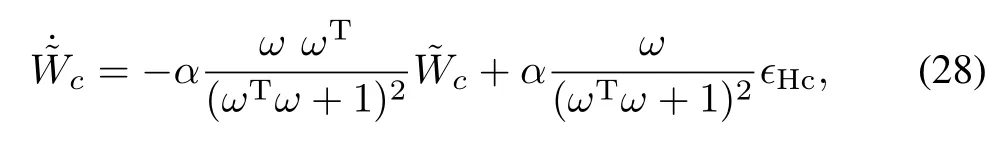
It is convenient to w rite the critic error dynamics as a sum of a nominal and a perturbed systemwhereand

Theorem 2.The nominal systemSnomis exponentially stable and its trajectories are satisfying‖c(t)‖ ≤‖c(t0)‖κ1e−κ2(t−t0),for someκ1,κ2∈R+fort＞t0≥0 provided that the signalis persistently exciting(PE)over the interval[t,t+T]w ithtt+T M MTdτ≥ γI,w ithγ∈R+andIis an identitymatrix of appropriate dimensions and also that there existsM B∈R+such that for allt≥t0,max{|M|,M}≤M B.

Proof.Consider the Lyapunov functionL:Rh→R,for allt≥0,

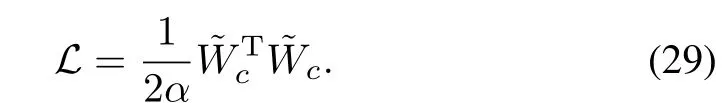
By differentiating(30)along theSnomone has

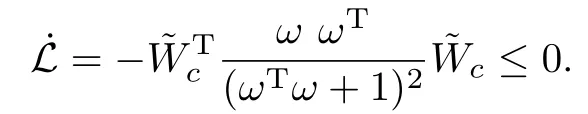
View ing the nom inal systemSnomas a linear time-varying system,the solutioncis given as(the reader is directed to[8]for the details)

where the state transition matrix is defined asTherefore we can prove that for the nominal system,the equilibrium point is exponentially stable provided thatMis PE and therefore for someκ1,κ2∈R+we can w rite∀t≥t0,

Finally by combining(31)and(32),we have

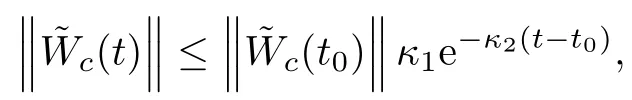
from which the result follows.

Remark 10.The above theorem designs an observer for the critic weights.It is shown in[17−19]thatκ1,κ2∈R+can be expressed as functions ofT,γ,BM.Based on the aforementioned papers we can prove the relaxed persistence of excitation condition(e.g.,u-PE).The interested reader is directed there formore details.

Now in order to find the tuning for the actor neuralnetwork we need to define the erroreu∈Rmin the follow ing form,

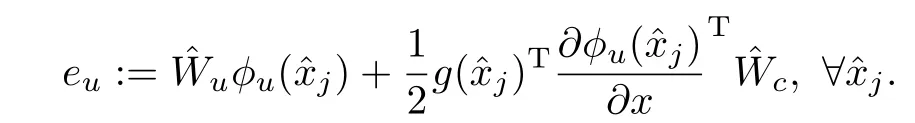
The nature of the update law for the actors w ill have an aperiodic nature and hence,it has to be updated only at the trigger instants and held constant otherw ise.This has a form of an impulsive system as described in[5,7].

We can then define the follow ing laws:

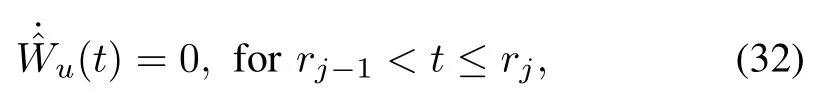
and the jump equation to computeu(r+j)given by

By defining the actor error dynam ics as˜Wu:=W∗u−ˆWuand taking the time derivative using the continuous update(33)and by using the jump system(34)updated at the trigger instants one has

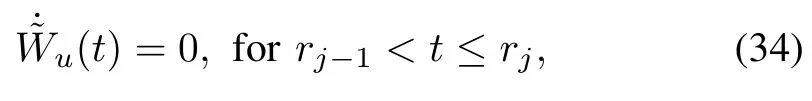
and

respectively.

B.Impulsive System Approach

Before we proceed to the design of the impulsive system the follow ing assumption is needed,

Assumption 3.The functiong(·)is uniform ly bounded onΩ,i.e.,supx∈Ω‖g(x)‖ ≤gmax.

Since the dynam ics are continuous but the controller jumps to anew valuewhen an event is triggeredweneed to formulate the closed-loop system as an impulsive system[5].But fi rstin order to deal w ith the presence of the neural network approximation errors and known bounds[20],and obtain an asymptotically stable closed-loop system one needs to add a robustifying term to the closed loop system of the form,

whereA,B∈R+satisfy

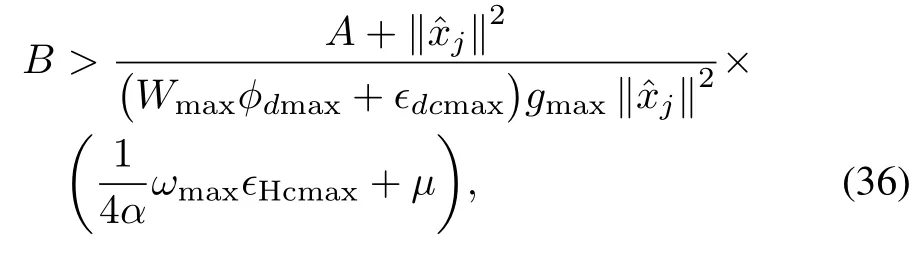
where

The closed-loop system dynamics(4)can now be w ritten as

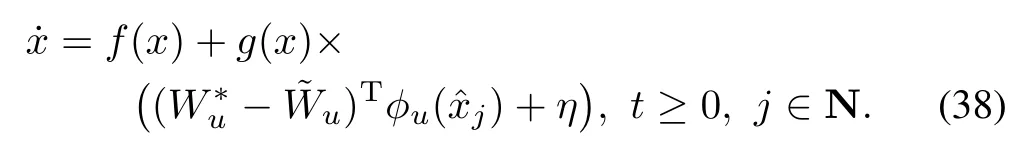
Finally we can combine the follow ing continuous and discrete time dynam ics(29),(35),(36),(39)by defining the augmentedstateψ:=[xTTjcTT]Tand after taking the time derivative fort∈(rj−1,rj],j∈N,

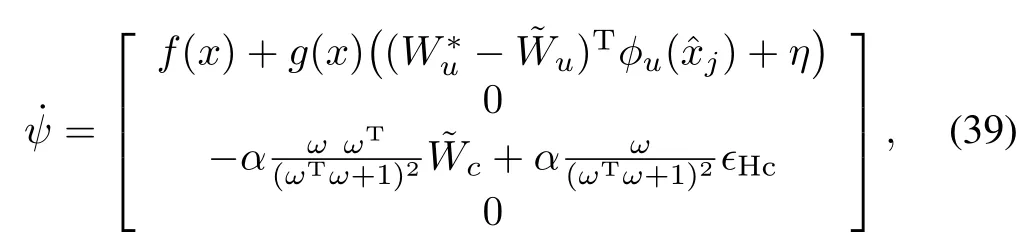
which are the dynamics while the controller is kept constant and the jump dynam ics fort=rjis given by

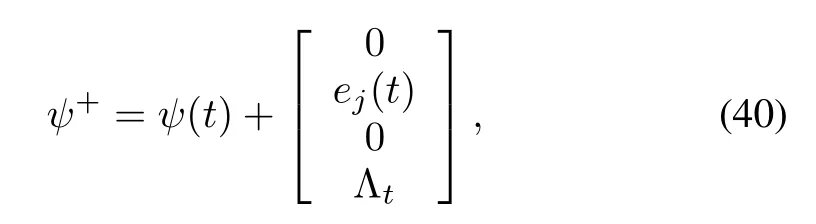
C.Convergence and Stability Analysis

Fact 1.The follow ing normalized signal satisfies:

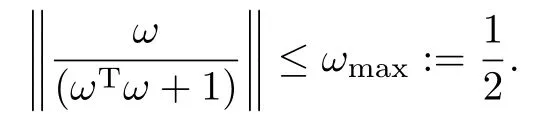
The follow ing theorem proves asymptotic stability of the impulsive closed-loop system described by(40)and(41),and convergence to the optimal solution.

Theorem 3.Consider the nonlinear continuous-time system given by(4)w ith the event-triggered control input given by(27)and the critic neural network given by(26).The tuning laws for the continuous-time critic and impulsive actor neural networks are given by(28),(33)and(34)respectively.Then there exists a quadruple⊂Ωw ithΩcompact such that the equilibrium point of the impulsive systemexists globally and converges asymptotically to zero for allx(0)insideΩx,j(0)inside,(0)insideandu(0)insidegiven the follow ing triggering condition:

whereβ∈(0,1)and the follow ing inequalities are satisfied:

for the critic neural network and

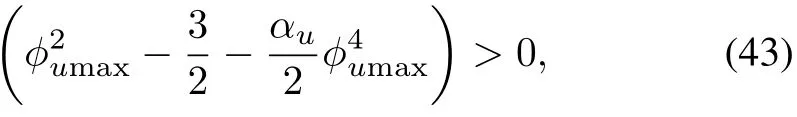
for the actor neural network.

Proof.In order to prove stability of the impulsive model,we have to consider the continuous and the jump dynam ics separately.Initially we w ill consider the follow ing Lyapunov functionV:Rn×Rn×Rh×Rh2→R for the continuous part(40)of the impulsivemodel,

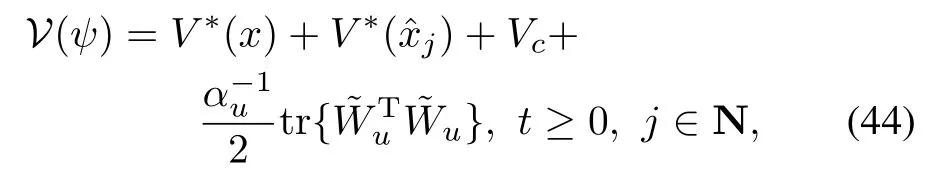
whereV∗(x)andV∗()are the optimal value functions for the continuou˜s sampled and event-triggered sampled system andVc:=‖Wc‖2is a Lyapunov function for the critic error dynam¡ ics¢ given by(29).Note thatVcsatisfieswhere the latter is a consequence of Theorem 2.

By taking the time derivative of(45)of the fi rst term w ith respect to the closed-loop system trajectories given by(39),the second term has a zero derivative,the third term w ith respect to the perturbed critic error estimation dynam ics(29),and substitute the actor dynam ics given by(33)(which are zero)for the last term one has(note that one can easily see the augmented state continuousdynamics in(40))∀j∈N andt≥0,

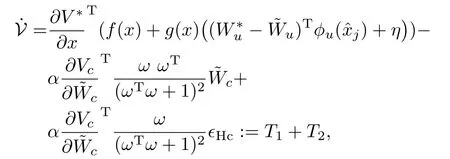
where for simplicity in the subsequent analysis we w ill consider the follow ing two terms and we w ill neglect the robustifying term for now:

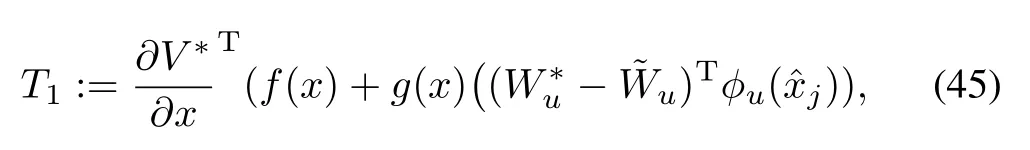
and

First we w ill simplify and upper bound the termT1from(46).In order to do that we w ill rew rite the time-triggered HJB equation(8)as

and after substituting(48)in(46),and usingandwe have

By using the Lipschitz condition from Assumption 1,we have

By substituting(50)in(49)and settingQ(x):=xTQxw ithQ≥0∈Rn×nwe have

after using(42).

Now for the termT2from(47)we have

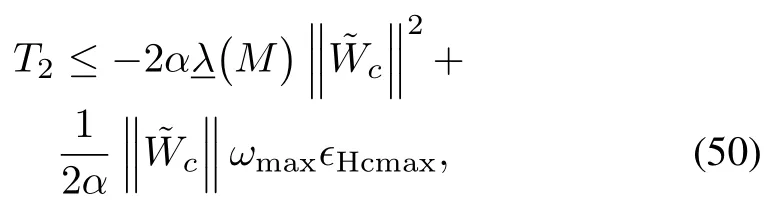
and after applying Young′s inequality at the second term of(51)one has

Note that the second term thathasknown boundsw illbe dealt from the robustifying termηas we shall see later(see(37))and by using the inequality(43)we can guarantee asymptotic stability of the critic neural network estimation error.

Now we have to consider the jump dynamics given by(41)which are the sampled statesand the actor neuralnetwork updates.For that reasonwew ill consider the follow ing difference Lyapunov function:

and since the states and the critic neural network estimation error are asymptotically stable,we have thatV∗(x+)≤V∗(x(rj))andA lso since we have proved that the states are asymptotically stable and since during the jump one haswe have thatThen one can w riteΔV(j):=wherekis a class-Kfunction[21].

Now we have to find a bound for the follow ing term:

where we have used the Frobenius no rm,Youn g′s inequality,and(34).By grouping the termsw ithtogetherwe have

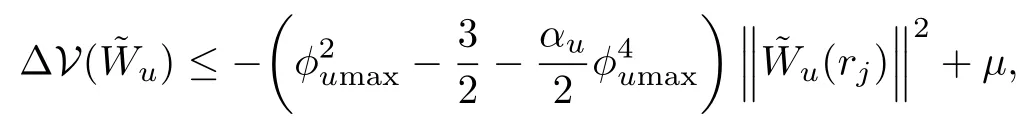
whereµis the known bound defined in(38)since we have proved that the critic neural network estimation error is asymptotically stable.Now we can either prove uniform ultimate boundedness(UUB)[21]as long as the sampled state satisfies,or the actor estimation errororwe can put the known bounds into the robustifying term[20]and prove asymptotic stability as long as(44)is true.The result holds as long as we can show that the statex(t)remains in the setΩ⊆Rnfor all times.To this effect,define the follow ing compact set:

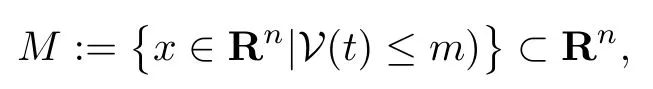
wheremis chosen as the largest constant so thatM⊆Ω.Since by assumptionx0∈Ωx,andΩx⊂Ωthen we can conclude thatx0∈Ω.Whilex(t)remains insideΩ,we have seen that≤0 and thereforex(t)must remain insideM⊂Ω.The fact thatx(t)remains inside a compact set also excludes the possibility of finite escape time and therefore one has global existence of solution.

V.SIMULATIONS

To support our theoretical developments and to show the advantages of an event-triggered optimal adaptive controller w ith respect to a time-triggered optimal adaptive controller as proposed in[22−23],two simulation examples are presented,one for an F16 aircraft plant and one for a nonlinear system,namely a Van-der PolOscillator.In both examples,the tuning gains are picked asα=20 andαu=0.2 andβ=0.7.

A.Aircraft Plant

Consider the F16 aircraft plant used in[24],

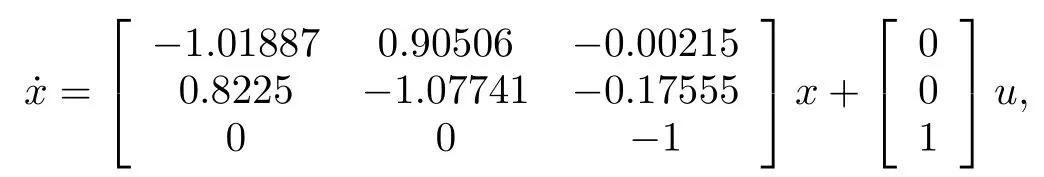
whereQ,Rare identity matrices of appropriate dimensions.If one solves the Riccati equation offl ine we w ill have,.The critic NN activation basis functionφ(x)are picked as quadratic in the state and the actor NN activation functions are picked asThe critic neural network of the optimal adaptive event-triggered algorithm presented in Theorem 3 converges to,=[1.4259 1.1713−0.1391 1.4412

−0.1498 0.4346]T.Theevolution of thesystem time-triggered state versus the event sampled state is presented in Fig.3.The event-triggered control input versus the time-triggered control input is presented in Fig.4 and the evolution of the sampledstates thatare used by the event-triggered controller are shown in Fig.5.In Fig.6,one can see that the event-trigger threshold converges to zero as the states converge to zero.A comparison between the event-triggered controller statemeasurements and the time-triggered controller is shown in Fig.7 where the event-triggered controlleruses less than 80 samplesof the state asopposed to the time-triggered controller thatusesmore than 700 samples.

B.Van-der Pol Oscillator

Consider the follow ing affine in control input Van-der Pol oscillator w ith a quadratic costw ithQthe identity matrix of appropriate dimensions andR=0.1 given by

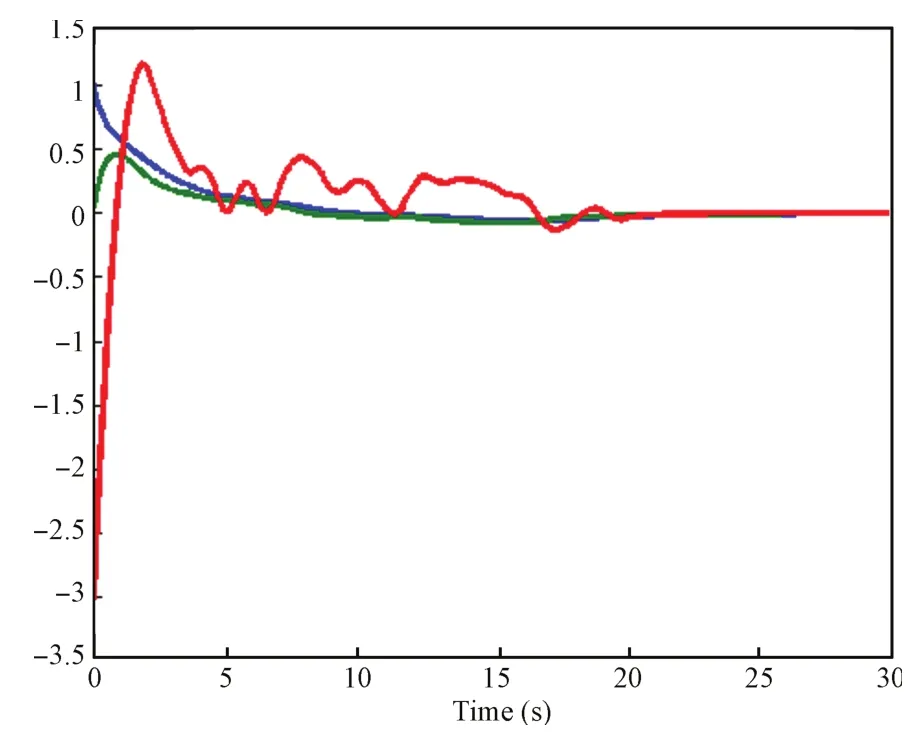
Fig.3. Evolution of the system states.

Fig.4. Event-triggered control input vs.time-triggered control input.

Fig.5. Sampled states used by the event-triggered controller.

Fig.6. Event-triggered threshold and triggering instants.

Fig.7. Number of state samples used.

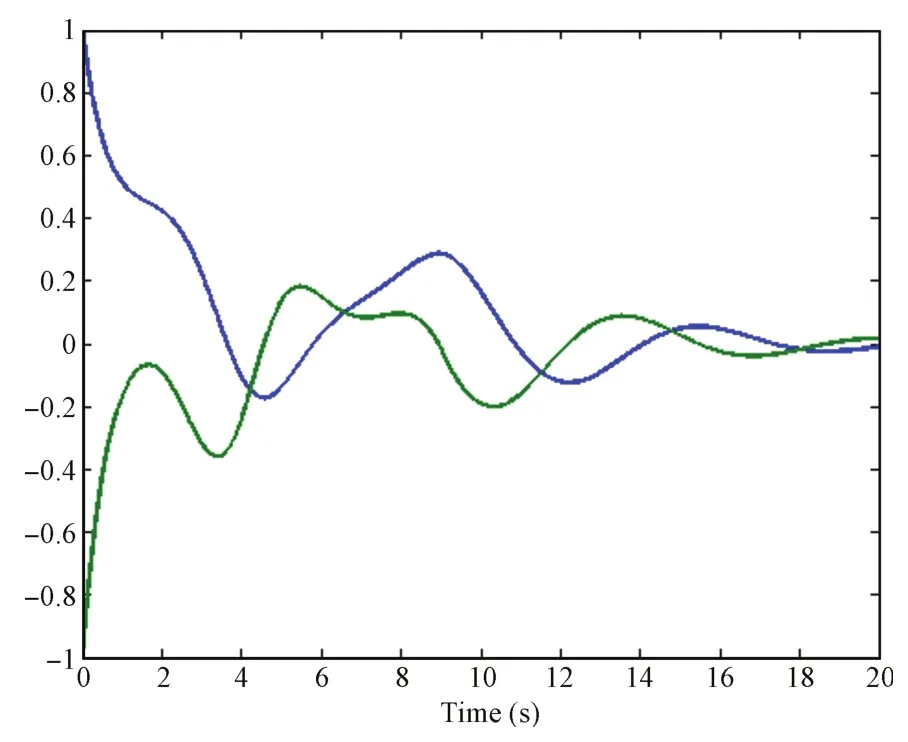
Fig.8. Evolution of the system states.

Fig.9. Event-triggered control input vs.time-triggered control input.

In Fig.11,one can see that the event-trigger threshold converges to zero as the states converge to zero.A comparison between the event-triggered controller statemeasurements and the time-triggered controller is shown in Fig.12,where the event-triggered controller uses 83 samples of the state as opposed to the time-triggered controller thatuses almost8000 samples,which is a great improvement in applications w ith bandw idth limitations and shared resources.Finally the interevent timesasa function of the time isshown in Fig.13,where one can see the significant improvementw ith respect to state transmissions.

Fig.10. Sampled states used by the event-triggered controller.

Fig.11. Event-triggered threshold and triggering instants.

VI.CONCLUSION AND FUTUREWORK

Thispaperhasproposed an optimaladaptiveevent-triggered control algorithm for nonlinear systems.The online algorithm is implemented based on an actor/critic neural network structure.A critic neural network is used to approximate the cost and an actor neural network is used to approximate the optimal event-triggered controller.Since in the algorithm proposed therearedynamics thatexhibitcontinuousevolutions described by ordinary differentialequations and instantaneous jumps or impulses,we used an impulsive system approach.Simulation results of an F16 aircraft plant and a controlled Van-der Poloscillator show the effectivenessand efficiency of the proposed approach in termsof control bandw idth and performance.Future work w ill be concentrated on extending the results in completely unknown systems and multiple decision makers.

Fig.12. Number of state samples used.

Fig.13. Inter-event times as a function of time.

[1]HeemelsW PM H,DonkersM C F,Teel A R.Periodic event-triggered control for linear systems.IEEE Transactions on Automatic Control,2013,58(4):847−861

[2]Lemmon M D.Event-triggered feedback in control,estimation,and optimization,.Networked Control Systems vol.405:Lecture Notes in Control and Information Sciences.Heidelberg:Springer-Verlag,2010.293−358

[3]Tabuada P.Event-triggered real-time scheduling of stabilizing control tasks.IEEE Transactions on Automatic Control,2007,52(9):1680−1685

[4]Lew is F L,Vrabie D,Vamvoudakis K G.Reinforcement learning and feedback control:using natural decision methods to design optimal adaptive controllers.IEEEControlSystems,2012,32(6):76−105

[5]Haddad W M,Chellaboina V,Nersesov S G.Impulsive and Hybrid Dynam ical Systems:Stability,Dissipativity,and Control.Princeton,NJ:Princeton University Press,2006.

[6]Hespanha JP,Liberzon D,Teel A R.Lyapunov conditions for inputto-state stability of impulsive systems.Automatica,2008,44(11):2735−2744

[7]Naghshtabrizi P,Hespanha J P,Teel A R.Exponential stability of impulsive systems w ith application to uncertain sampled-data systems.Systemsand Control Letters,2008,57(5):378−385

[8]Donkers M C F,Heemels W P M H.Output-based event-triggered control w ith guaranteed L∞-gain and improved and decentralised event-triggering.IEEE Transactions on Automatic Control,2012,57(6):1362−1376

[9]Wang X,Lemmon M D.On event design in event-triggered feedback systems.Automatica,2012,47(10):2319−2322

[10]Demir O,Lunze J.Cooperative control of multi-agent systems w ith event-based communication.In:Proceedings of the 2012 American Control Conference.Montreal,QC:IEEE,2012.4504−4509

[11]Lehman D,Lunze J.Event-based control w ith communication delays.In:Proceedingsof the 2011 IFACWorld Congress.M ilano,Italy:IFAC,2011.3262−3267

[12]Molin A,Hirche S.Suboptimal event-based control of linear systems over lossy channels estimation and control of networked systems.In:Proceedings of the 2nd IFACWorkshop on Distributed Estimation and Control in Networked Systems.Palace,France:IFAC,2010.55−60

[13]Garcia E,Antsaklis P J.Model-based event-triggered controlw ith timevarying network delays.In:Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference.Orlando,FL:IEEE,2011.1650−1655

[14]Lew is F L,Syrmos V L.OptimalControl.New York:JohnWiley,1995.

[15]Barradas B,de Jesu´s J,Gommans T M P,Heemels M.Self-triggered MPC for constrained linear systemsand quadratic costs.In:Proceedings of the 2012 IFAC Conference on Nonlinear Model Predictive Control.Leeuwenhorst,Netherlands:IFAC,2012.342−348

[16]Ioannou P A,Fidan B.Adaptive Control Tutorial.Advances in design and control,SIAM(PA),2006.

[17]Lor´ıa A.Explicit convergence rates for MRAC-type systems.Automatica,2004,40(8):1465−1468

[18]Lor´ıa A,Panteley E.Uniform exponentialstability of linear time-varying systems:revisited.Systemsand Control Letters,2003,47(1):13−24

[19]Panteley E,Loria A,Teel A.Relaxed persistency of excitation for uniform asymptotic stability.IEEE Transactions on Automatic Control,2001,46(12):1874−1886

[20]Polycarpou M,Farrell J,Sharma M.On-line approximation control of uncertain nonlinear systems:issues w ith control input saturation.In:Proceedings of the 2003 American Control Conference.Denver,CO:IEEE,2003:543−548

[21]Khalil H K.NonlinearSystems.New Jersey:Prentice Hall,2002.

[22]Vamvoudakis K G,Lew is F L.Online actor-critic algorithm to solve the continuous-time infinite horizon optimal control problem.Automatica,2010,46(5):878−888

[23]Vrabie D,Vamvoudakis K G,Lew is F L.Optimal adaptive control and differential games by reinforcement learning principles.Control Engineering Series.New York:IET Press,2012.

[24]Stevens B,Lew is FL.AircraftControland Simulation(Second Edition).New Jersey:John Willey,2003.

[25]Nevistic´ V,Primbs J A.Constrained Nonlinear Optimal Control:A Converse HJB Approach,Technical Memorandum No.CIT-CDS 96-021,1996.