极限平衡有限元在边坡稳定性分析中的应用

杨宏宇，白伟明，邹洪海

（青岛海洋地质研究所，山东 青岛 266071）

0 引 言

边坡失稳是工程安全的热点问题[1-2]。实际工程中，边坡稳定性分析方法主要采用刚体极限平衡分析方法[3]。由于天然岩土体应力状态受岩土介质变形与强度特性的共同控制，采用刚体极限平衡分析方法评价边坡稳定性时又需对滑体条间应力进行假设，计算结果往往不尽人意。同样，采用基于经典数学物理方程与计算机技术的数值分析方法，虽然可得到边坡应力场，且满足应力变形协调条件，但却又无法给出边坡的安全系数。因此，若能将两者有效联系，则既可克服刚体极限平衡分析不满足应力变形协调原理的缺陷[4-5]，又可得到更为合理的安全系数。

边坡稳定性计算的关键是确定出滑面并获得滑面法向、切向力[6]。当采用刚体极限平衡分析时，不同的条分法计算结果间往往存在一定偏差[7]，且仅当条分底面法向和切向力与真实值较为接近时，计算结果才比较理想。为此，国内外许多学者尝试通过结合优化理论或基于有限元分析方法来提高计算的有效性，如动态规划法[8]、遗传算法等，均有效克服了安全系数局部最优的不足[9]。

本文以有限元数值计算所得的边坡应力场为基础，通过指定一个搜索区域，将其格栅化后，以格栅节点控制圆弧形滑移面圆心，不断迭代试算，确定边坡最危险滑移面位置及安全系数，然后将其与刚体极限平衡分析结果对比，以此验证采用数值极限平衡有限元法分析边坡稳定的适用性。

1 边坡滑面搜索流程

边坡失稳是边坡体内部应力和强度变化的结果，故边坡安全与其应力状态密切相关。以有限元数值计算获取边坡应力场进行极限平衡分析，可弥补刚体极限平衡分析法不满足应力变形协调原理的缺陷，使所得的边坡最危险滑面及安全系数更为合理、准确。本文采用滑面圆心格栅化控制法确定最危险滑面，具体计算流程如下：

（1）预先指定滑面圆心搜索范围，并对搜索范围进行格栅化。

（2）依次选取格栅点作为滑面圆心，以坡脚可能发生剪出的范围内任意一点作为滑面上一点，确定滑面及滑面方程。

（3）将步骤（2）中确定出的当前滑面离散化 （即按滑面穿过的单元大小将整个滑面划分为小的弧段），以弧段中心为控制点搜寻每个弧段所穿过的单元位置，并根据单元节点应力计算出穿过该单元的弧段上的法向力和沿弧段的切向力。

（4）累计所有滑弧段的抗滑力与滑动力获得滑面抗滑力与滑动力，从而计算出当前滑动面的安全系数，若当前计算结果小于先前计算值，更新全局安全系数及滑面位置。

（5）遍历所有网格格栅点，即可确定出边坡安全系数及最危险滑面位置。

2 工程实例

2.1 模型及参数

边坡模型尺寸见图1，斜坡坡脚为45°。为简便模型构建，边坡材料视为均质、各向同性的单一材料，其相应的材料参数见表1。有限元网格见图2。模型由2 551个单元，5 338个节点构成。

图1 边坡几何尺寸（单位：m）

表1 材料参数

图2 有限元网格模型

2.2 计算结果

边界约束采用位移约束，即固定模型左右及下边界，然后应用经典的More-Columb屈服准则进行应力场的有限元数值模拟，所得主应力、应力分量见图3。塑性区见图4。

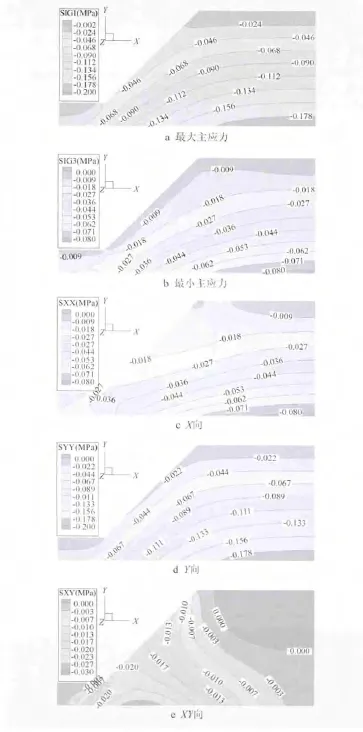
图3 主应力、应力分量（单位：MPa）

计算结果表明，最大主应力－0.178 MPa，最小主应力－0.080 MPa，均表现为压应力，坡脚位置应力变化较其他部位相对复杂；水平向 （X方向）和竖直向 （Y方向）应力变化表现出相同的规律；坡脚XY方向应力变化剧烈，出现剪切塑性区，故可断定最危险滑面剪出口位置应该位于坡脚处，该结果同时可作为极限平衡稳定性分析滑面剪出口位置选择。

图4 剪切塑性区

2.3 稳定性分析

边坡稳定分析的关键问题是确定出合理的最危险滑动面位置及相应的安全系数。许多情况下，在采用刚体极限平衡分析法进行边坡稳定性分析时发现，搜寻出的边坡安全系数小于1.0，而实际边坡仍然处于稳定状态，计算结果与实际情况矛盾，此时的刚体极限平衡分析结果具有局限性。本文将有限元计算所得单元应力、应变、位移等结果引入到求解边坡临界滑动面安全系数中，建立了数值计算与滑坡稳定评价的联系，考虑了滑体条间应力假设的不足，克服了刚体极限平衡分析法不满足应力变形协调的缺陷，可有效地确定出边坡最危险滑移面位置及安全系数。

以有限元数值计算所得的应力场为基础，应力变形分析结果为参照，即以坡脚位置作为剪出口，边坡左上侧区域格栅节点控制圆弧形滑面圆心，进行边坡最危险潜在滑面位置搜索及安全系数的迭代计算，最终确定出边坡最危险滑面位置及安全系数。刚体极限平衡法 （包括Bishop法、Janbu修正、Spencer法和M-P法）与极限平衡有限元法最危险滑面搜寻结果见图5。由于刚体极限平衡计算结果非常相近，搜寻滑面重合，故图5中刚体极限平衡滑面仅1条。将其与极限平衡有限元法搜寻结果对比发现，极限平衡有限元所得滑面位置较刚体极限平衡结果更靠近边坡内，主要是由于刚体极限平衡分析法将土条视为刚体，没有考虑边坡土体在天然状态下产生塑性变形时应力应变场的变化，从而导致了分析结果间的差异。

表2为采用不同的方法计算所得的安全系数。从表2可知，刚体极限平衡分析计算的安全系数均值为1.469，极限平衡有限元计算所得安全系数为1.516，两者结果相近，具有一致性，说明数值极限平衡有限元法是有效的，可合理确定出边坡最危险滑面位置及安全系数，特别是对已经产生塑性变形的边坡将更具适用性。而对于土钉、锚杆、锚索等支护边坡的稳定性计算及优化设计，采用极限平衡有限元计算分析亦可很好地解决其在复杂应力状态下的安全分析与评价问题。

图5 不同方法计算的最危险滑面位置

表2 不同方法计算的安全系数

3 结 论

（1）边坡极限平衡有限元分析考虑了滑体条间应力假设的不足，克服了刚体极限平衡分析法不满足应力变形协调的缺陷，可确定出边坡最危险滑面位置及安全系数。

（2）对已产生塑性变形的边坡进行安全性评价时，极限平衡有限元法比刚体极限平衡分析法更具适用性。

［1］ 王玉平，曾志强，潘树林.边坡稳定性分析方法综述［J］.西华大学学报：自然科学版,2012，31（2）:101-105.

［2］ SHI Chong,ZHANG Yulong,ZHANG Qiang.Safety factor calculation method of anchored slope based on pseudo cohesion theory ［J］.Applied Mechanics and Materials,2012,170-173:453-456.

［3］ 陈祖煜.土质边坡稳定分析原理·方法·程序［M］.北京：中国水利水电出版社，2003.

［4］ TURNER J P,JENSEN W G.Landslide stabilization using soil nail and mechanically stabilized earth walls： Case study［J］.J.of Geotech.and Geoenvirn.Eng.,ASCE,2005,131（2）:141-150.

［5］ COTTON P E,DAVID M,LUARK P F.Seismic response and extended life analysis of the deepest top-down soil nail wall in the U.S［J］.Geotechnical Special Publication,2004,124（3）:723-740.

［6］ 徐卫亚，周家文，邓俊晔，等.基于Dijkstra算法的边坡极限平衡有限元分析［J］.岩土工程学报， 2007， 29（8）:1159-1172.

［7］ 张鹏.岩土边坡刚体极限平衡法的误差根源与范围研究［D］.西安：西安理工大学，2003.

［8］ 范鹏贤，朱大勇，郭志昆，等.动态规划法求解边坡安全系数最小上限解［J］.岩土工程学报， 2007， 29（3）:467-470.

［9］ 陈云敏，李育超，凌道盛.蒙特卡洛法与有限元结合搜索边坡临界滑动面［J］.岩土力学， 2004， 25（S2）:75-80.