电火花线切割机床四轴联动单位弧长增量插补法

陈默，陈昊，赵万生

（上海交通大学机械与动力工程学院机械系统与振动国家重点实验室，上海 200240）

电火花线切割机床四轴联动单位弧长增量插补法

陈默，陈昊，赵万生

（上海交通大学机械与动力工程学院机械系统与振动国家重点实验室，上海 200240）

提出了一种单位弧长增量插补法，其主要思路为：每个插补周期沿曲线增加一个单位弧长增量，累计各轴所对应的增量，每溢出一次，该进给轴输出一个单位脉冲增量。通过定义广义弧长参数，将上下异形面中较短的曲线进行重新参数化，以曲线坐标值增量表达式的泰勒展开式为依据，实现了对上下异形面的四轴联动一步式直接插补。仿真实验结果表明：该方法还具有误差更小、存储空间需求更小的优点。

电火花线切割加工；单位弧长增量插补法；四轴联动

电火花线切割机床以其特殊的扫掠式加工方式，被广泛应用于直纹面工件的加工。随着工件形状的不断复杂化，线切割加工中针对上下异形面的变锥度加工功能也变得越来越重要。变锥度加工运动控制的关键技术在于规划四轴的运动，使上下异形面工件的上、下平面的曲线插补在满足一定精度要求的条件下同步协调进行。吕晓纲等提出了一种表面轨迹直控法，对上、下平面的曲线分别进行插补计算，再引入行程协调函数来决定上、下平面的插补次序[1]。袁立新等在表面轨迹直控法的基础上，增加了对相邻的上、下平面插补进行合并的步骤，减小了上、下导轮反复进退所带来的速度变化[2]。刘康等设计了双插补器，2个插补器分别用于插补工件上、下平面曲线和上、下导轮运动轨迹曲线[3]。

一些现有方法对各平面曲线的插补采用脉冲增量法（如逐点比较法、数字积分法、最小偏差法等），其局限性在于：对于圆的插补需进行过象限判别；沿曲线的插补进给速度不均匀，导致对上下异形面插补的精确等比例控制过程变得困难与复杂；不适用于复杂参数曲线（如NURBS曲线）的插补。Yang等提出了一种基于数据采样法的线切割NURBS曲线轨迹插补法[4]，即用小直线段对NURBS曲线进行逼近（粗插补），再对小直线段做精插补；粗插补带来的弦高误差导致其精度比采用脉冲增量法低，且需生成大量的小直线段，从而形成长篇的G代码，消耗了大量的存储空间。此外，上述方法的思路均是将线切割加工运动轨迹插补过程分为“单曲线插补+协调”两步进行。为了实现对上下异形面或锥面线切割加工轨迹的高精度四轴联动一步式直接插补，本文提出了单位弧长增量插补法。

1 四轴联动单位弧长增量插补法原理

1.1 单位弧长增量插补法原理

上下异形面或锥面线切割加工运动轨迹的四轴联动插补与其他机床加工运动轨迹插补的一大区别在于：需保证上下异形面插补具有良好的同步性，即两条曲线的插补要按等比例的进度执行，而进度的比较依据则是两条曲线的弧长。因此，有必要引入以弧长为参数的插补方法，根据每个插补周期内的弧长参数增量来决定各轴是否进给。

如图1a所示，对于平面曲线，以弧长s作为参数的表达式：

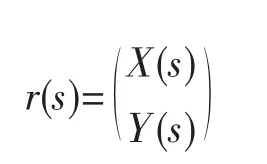
为了便于对算法进行统一描述，以x1代替X、以x2代替Y来表示曲线坐标，即：

图1 单位弧长增量插补法示意图

如图1b所示，在每个插补周期内沿曲线运动一小段距离，这一小段运动轨迹在每个坐标轴上将产生一段投影直线；将这些投影直线段的长度以机床的脉冲当量BLU为单位进行表示，其数值的近似整数值就是当前插补周期内各轴的进给脉冲数。由于机床运动的分辨率是由各轴BLU对应的长度决定的，因此，为了保证插补轨迹能最大程度地拟合原始曲线，取弧长参数增量△s=1 BLU，使每个插补周期内的每个坐标增量的绝对值≤1 BLU。每个坐标值的增量计算式为：

式中：第2个等号将坐标值增量做m阶泰勒展开，一般情况下，根据曲线的不同取m=1或m=2，可满足精度要求。由此可见，采用式（1）直接计算坐标值增量需引入浮点数操作。要避免浮点数操作，可将其凑成如下形式：

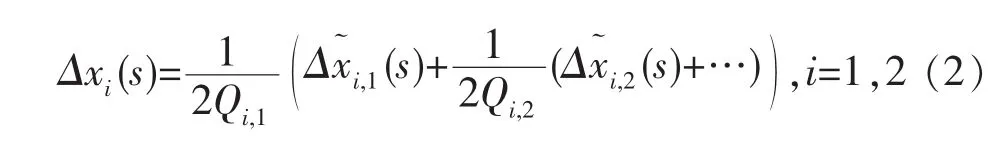
式中：△x～i,j(s)为i轴的j阶增量当量；Qi,j为i轴的j阶阈值。式（2）就是单位弧长增量法的插补递推式。

为了便于说明式（1）和式（2）之间的关系，下面以圆弧插补为例进行介绍。圆弧的弧长参数表达式为：

式中：θs为圆弧的起始角，为便于说明，取其值为0；R为圆弧半径；k为圆弧方向系数，当k=1时，为逆时针插补；当k=-1时，为顺时针插补。由式（1）求坐标值增量表达式的泰勒展开式，取展开阶数m=2，可得：

比较式（2）、式（3）、式（4）可知各轴各阶增量当量：

以及相应的阈值：

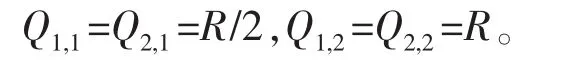
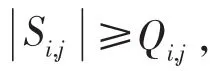
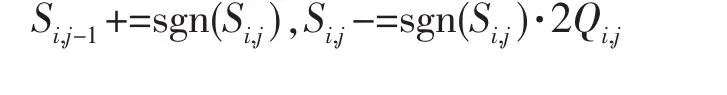
第1个式子表示将sgn(Si,j)加入累加器Si,j-1中，第2个式子表示从累加器Si,j中减去sgn(Si,j)·2Qi,j，符号函数为：

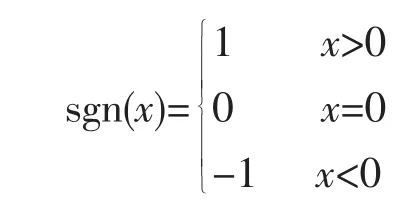
注意到零阶累加器Si,0实际上就是第i轴的坐标值，其值按一阶累加器Si,1的进位情况进行改变。上述计算过程实质上类似于实数加减法计算（图2）。重复进行该计算过程，直到累计弧长值s大于或等于原始曲线的总弧长L，完成对整条曲线的插补。

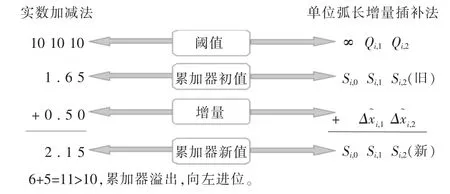
图2 实数加减法计算与单位弧长增量插补法计算的类比

与脉冲增量法相比，单位弧长增量法在每个插补周期内以固定的单位弧长增量沿弧线进给，使进给速度更均匀；在插补圆弧时，无需做过象限判别，简化了算法。与数据采样法相比，单位弧长增量法避免了采用小线段逼近原始曲线的粗插补过程，直接对曲线进行精插补，具有更高的插补精度。此外，单位弧长增量插补法以曲线表达式的弧长参数方程的泰勒展开式为基础，对参数曲线具有普适性，使线切割加工上下异形面或锥面变得异常简单；另一方面，插补的终点判别是以弧长来计算，也避免了指定某个轴的进给长度所带来的欠进给误差。

1.2 上下异形面四轴联动一步式直接插补的实现

上下异形面的线切割加工路径插补问题可归结为对工件上、下平面加工路径曲线的同步插补问题（图3）。

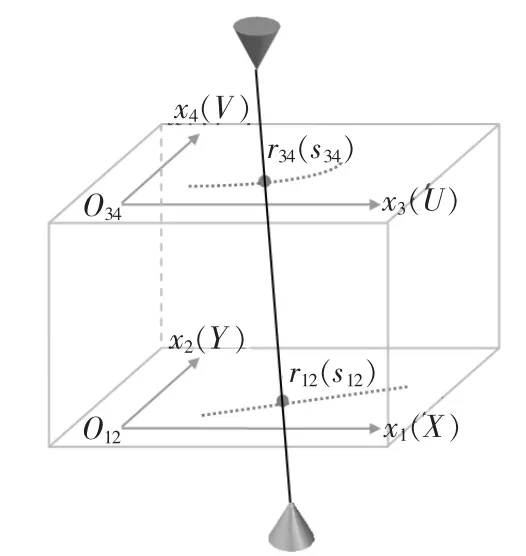
图3 线切割加工轨迹插补示意图

以（x1，x2）表示下平面曲线的坐标（X、Y）、（x3，x4）表示上平面曲线的坐标（U、V），则上、下平面曲线的弧长参数表达式为：

式中：s12和s34分别为下平面曲线和上平面曲线的弧长参数。要使两条曲线的插补同时开始、同时结束，就需使每个插补周期内两条曲线的弧长参数保持如下比例关系：

式中：L12和L34分别为下平面曲线和上平面曲线的弧长。设：

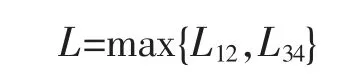
不失一般性，设L12＞L34，则L=L12，定义广义弧长参数：

并根据式（7）对上平面曲线做参数变换：

将式（8）和式（9）代入式（5）和式（6），并将两条曲线的表达式合写为一个表达式：

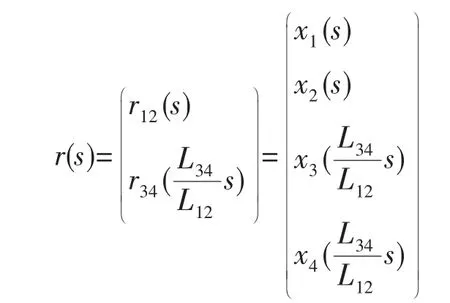
这样，对上下异形面的插补就化为对一条以广义弧长s为参数的四维空间的曲线的插补。根据前节的单位弧长增量插补法，对该曲线表达式中的各元素做泰勒展开并化为式（2）的形式，获得增量当量△x～i,j(s)和阈值Qi,j，再设置累加器Si,j，即可实现对该曲线的插补。L34＞L12的情形与L12＞L34的情形类似，只是广义弧长定义为s=s34，并对下平面曲线做参数变换。两种情形对曲线的变换结果可归结为：

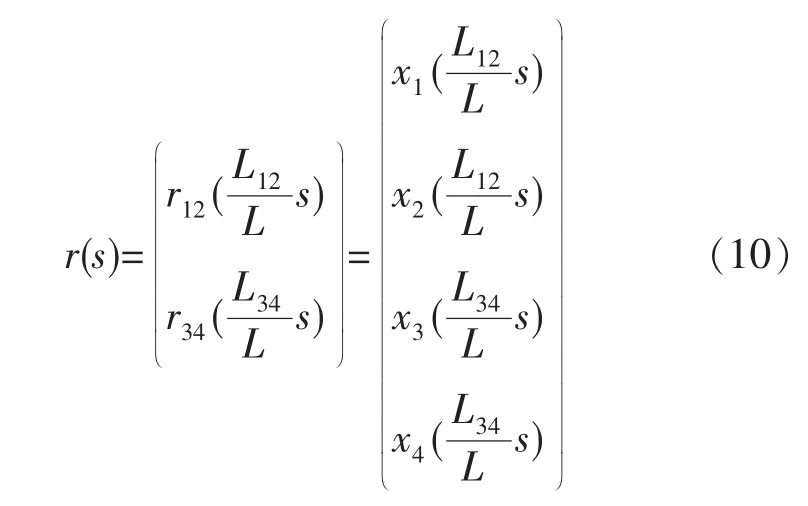
插补的流程见图4。可见，通过对短曲线的重新参数化，将两条曲线化为一条曲线，无需额外增加行程协调的步骤，实现了对上下异形面的一步式直接插补。

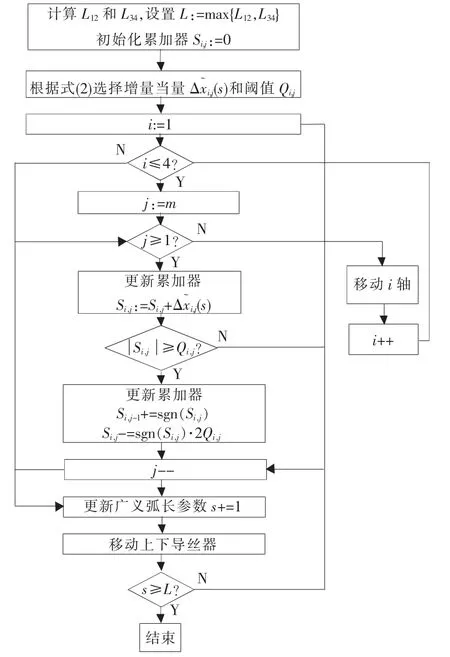
图4 插补流程图

2 仿真实验

以“天圆地方”形状的工件为例，根据其对称性，取其中1/4的加工轨迹进行插补仿真实验（图5）。加工轨迹的上下异形面加工参数见表1，其中机床的分辨率为1 μm=1 BLU。

并与式（2）比较，可知各轴各阶增量当量为：

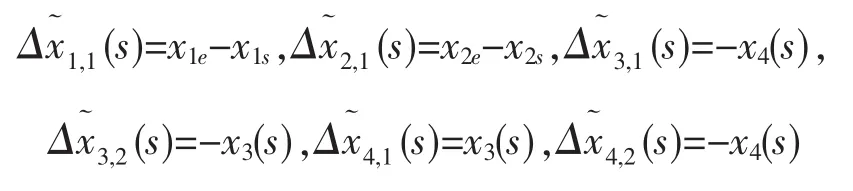
相应的阈值为：

表1 仿真加工轨迹数据

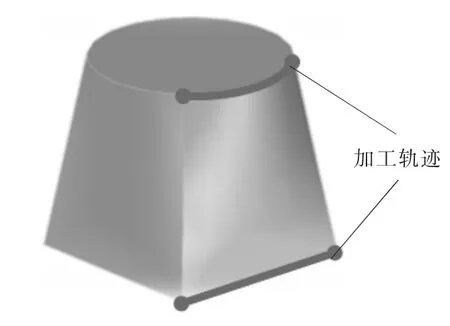
图5 加工仿真轨迹（加粗曲线）

由图5可看出，下平面轨迹为直线，计算弧长得L12=10 000 BLU；上平面轨迹为逆时针圆弧（k= 1），计算弧长得L34=7854 BLU。因此，L12＞L34，L=L12，定义广义弧长参数s=s12。根据式（10），可得四维空间中的曲线表达式：

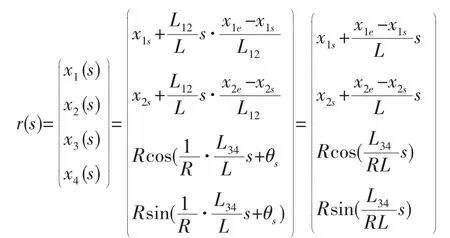
根据式（1），对坐标值增量表达式做泰勒展开，其中，直线和圆弧的增量表达式分别展开至1阶和2阶，得：

基于上述计算结果，以单位弧长增量法进行插补，并与数据采样法（允许最大弦高误差为0.5 BLU的粗插补与脉冲增量法精插补相结合）的插补结果进行对比（表2）。

表2 仿真结果

由仿真结果可见，数据采样法的插补误差比单位弧长增量法都大，这是由于数据采样法的粗插补采用了小直线段逼近曲线而引起了弦高误差，且精插补的脉冲增量法也会带来一定的误差，两个误差的叠加结果较大。此外，数据采样法的粗插补阶段获得的一系列小直线段，使CAM软件生成较多的G代码指令；而单位弧长增量法只需一条G代码就能表示一对曲线，大大节省了插补器的存储空间。

3 结论

通过定义广义弧长参数，将单位弧长增量插补法应用于线切割上下异形面的插补。与传统方法相比，其优势在于：

（1）避免了采用小直线段逼近原始曲线所带来的弦高误差，提高了插补精度，减少了插补器所需的存储空间。

（2）以曲线坐标增量表达式的泰勒展开式为插补依据，上、下平面曲线的类型不再限于直线和圆。

（3）对于直线和圆的插补，可避免浮点数运算，且误差不大于1 BLU。

（4）对于圆的插补，无需过象限判别。

（5）四轴联动一步式直接插补方式保持了上下异形面等比例匀速插补，无需引入行程协调函数。

因此，由单位弧长增量插补法的原理可见，其不但适用于线切割加工轨迹的插补，也适用于带旋转轴的多轴联动同步插补，在高精度、高可达性的机床中具有广泛的应用前景。

[1]吕晓纲，金志强.线切割上下异形锥度曲面加工控制的研究[J].电加工，1998（5）：41-43.

[2]袁立新，谭锡林.四轴联动线切割双平面插补控制的研究[J].电加工与模具，2001（5）：16-18.

[3]刘康，柳忠彬，胡光忠，等.线切割上下异形锥度加工的双插补控制算法的实现[J].机床与液压，2011，39（8）：26-28.

[4]Yang M Y，Park J H.A study on an open architecture CNC system with a NURBS interpolator for WEDM[J]. The International Journal of Advanced Manufacturing Technology，2002，19（9）：664-668.

“电加工技术发展规划专题研讨会”在苏州召开

为了集思广益，提出电加工技术在高档数控机床与基础制造装备专项（04专项）“十三五”期间发展规划的建议，中国机械工程学会特种加工分会和中国机床工具工业协会特种加工机床分会邀请我国电加工领域20余名专家，于2014年7月23日在苏州召开了电加工技术发展规划专题研讨会。

中国科学院院士、中国机械工程学会特种加工分会理事长、南京航空航天大学朱荻教授主持了会议。中国机床工具工业协会特种加工机床分会理事长、中国机械工程学会特种加工分会荣誉理事长、苏州电加工机床研究所有限公司董事长叶军研究员介绍了工信部正在制定的04专项“十三五”发展规划相关情况，并提出了电加工（包括电火花加工和电化学加工）技术发展规划建议框架。与会代表围绕这一框架，就电加工技术及装备的发展建议进行了深入的讨论。大家认为，“十三五”期间要以电加工技术及产品研发创新基本能力的建设为主线，加强电加工关键基础共性技术的研究，加强研发、试验、检测平台的建设，进一步加强产、学、研、用的合作，集聚优势资源，借鉴追赶与自主创新相结合，扎实、系统地突破和提升一批电加工关键基础共性技术，进一步提升高端电加工主导产品的技术水平和市场竞争力，并为我国航天、航空、航海、军工等重要领域提供具有更高水平和独具特色的产品。

根据会议研讨的结果，就电加工关键共性技术的攻关及研究实验平台的建设、高端电加工主导产品性能水平的提升、电加工专项技术及专用设备的研制、国家级电加工重点实验室及工程技术中心的建设等形成了具体的意见和建议。

（特种加工分会）

Four-axes Drived Unit Arc Length Increment Method for WEDM

Chen Mo，Chen Hao，Zhao Wansheng
（Shanghai Jiao Tong University，Shanghai 200240，China）

This paper proposes a unit arc length increment method which in each interpolated period，the curve increases one basic arc length unit(BLU)，while cumulated the increments of each axis overflows，the axis generate one unit pulse increment.The generalized arc length parameter is defined to reparameterize the shorter curve，and a ruled surface is directly interpolated by using the Taylor expansions of incremental functions of coordinates.Simulation results show that the proposed method gives less error and requires less memory space.

WEDM；unit arc length increment method；four-axes drived

TG661

A

1009－279X（2014）04－0013-05

2013-12-30

国家自然科学基金资助项目（51175337）；机械系统与振动国家重点实验室项目（MSVMS201111）

陈默，男，1986年生，博士研究生。