关于圆周率的又一种解法
2018-03-14吴润鑫
数学学习与研究 2018年3期
吴润鑫

【摘要】本文基于初等数学的几何与代数方法,同时应用高等数学的极限思想,提出圆周率的正弦与正切表达式.当循环次数大于10时,该计算方法可准确得到圆周率的小数点后5位;当循环次数大于25时,该计算方法可准确得到圆周率的小数点后14位;当循环次数大于30时,该计算方法可准确得到圆周率的小数点后15位.本方法可以作为计算π的一种简单、有效的方法.
【关键词】圆周率;三角函数;圆心角;弧长;无限分割
一、引 言
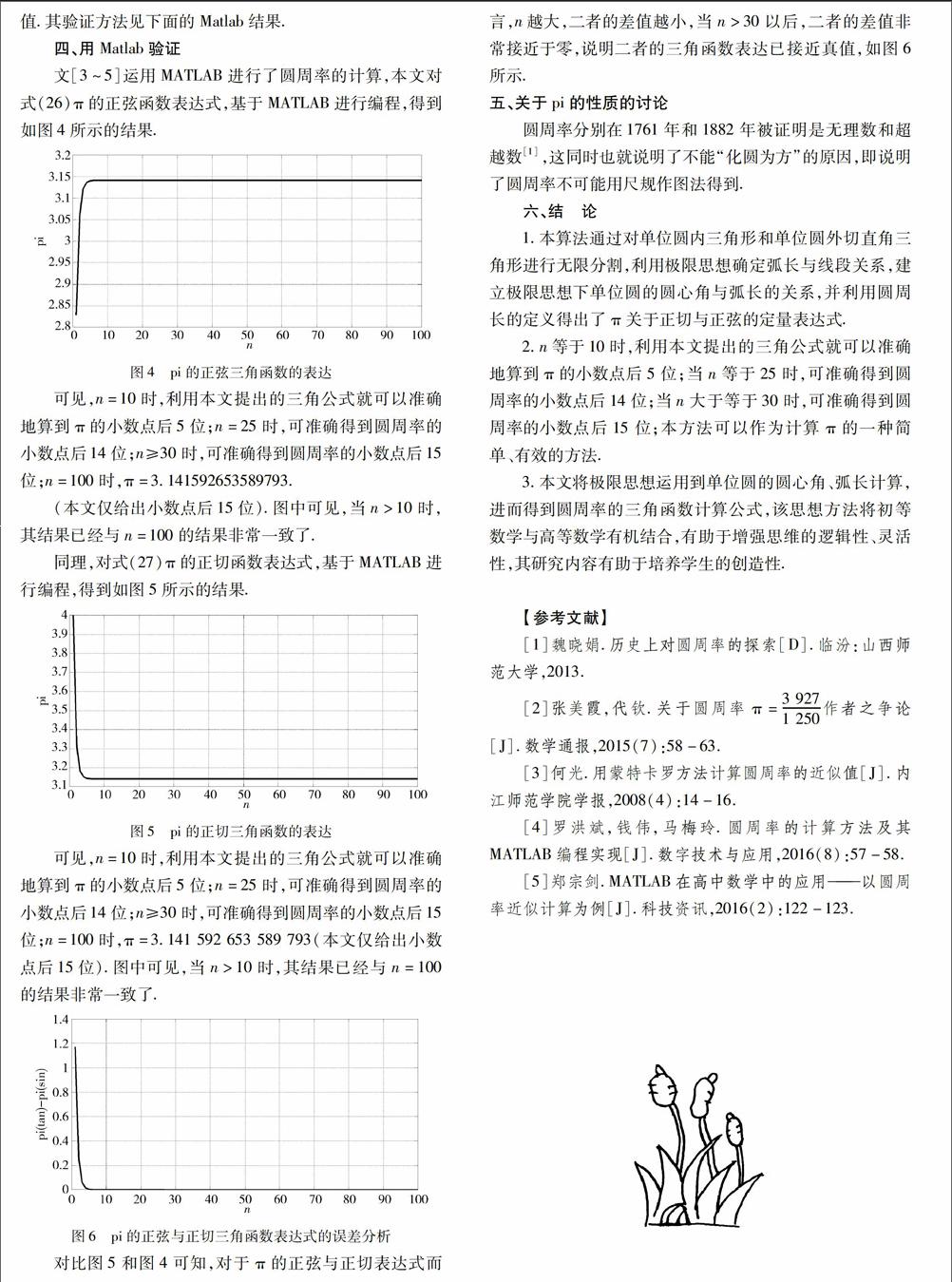
圆周率用希腊字母π表示.公元前3世纪之前,古巴比伦、古印度和古代中国分别开始研究圆周率的计算;公元前3世纪,古希腊阿基米德计算圆周率在3~4之间;公元3世纪,中国刘徽提出割圆法,得到圆周率的4位精度;公元5世纪,中国祖冲之得到圆周率7位精度,并得到两个近似值.1 200年后,1609年德国鲁道夫得到圆周率35位精度,1761年,瑞士兰伯特证明圆周率是无理数,1882年,德国林德曼证明圆周率为超越数.电子计算机的出现使π值计算有了突飞猛进的发展,如今,计算机已算到π的后几千万亿位小数.
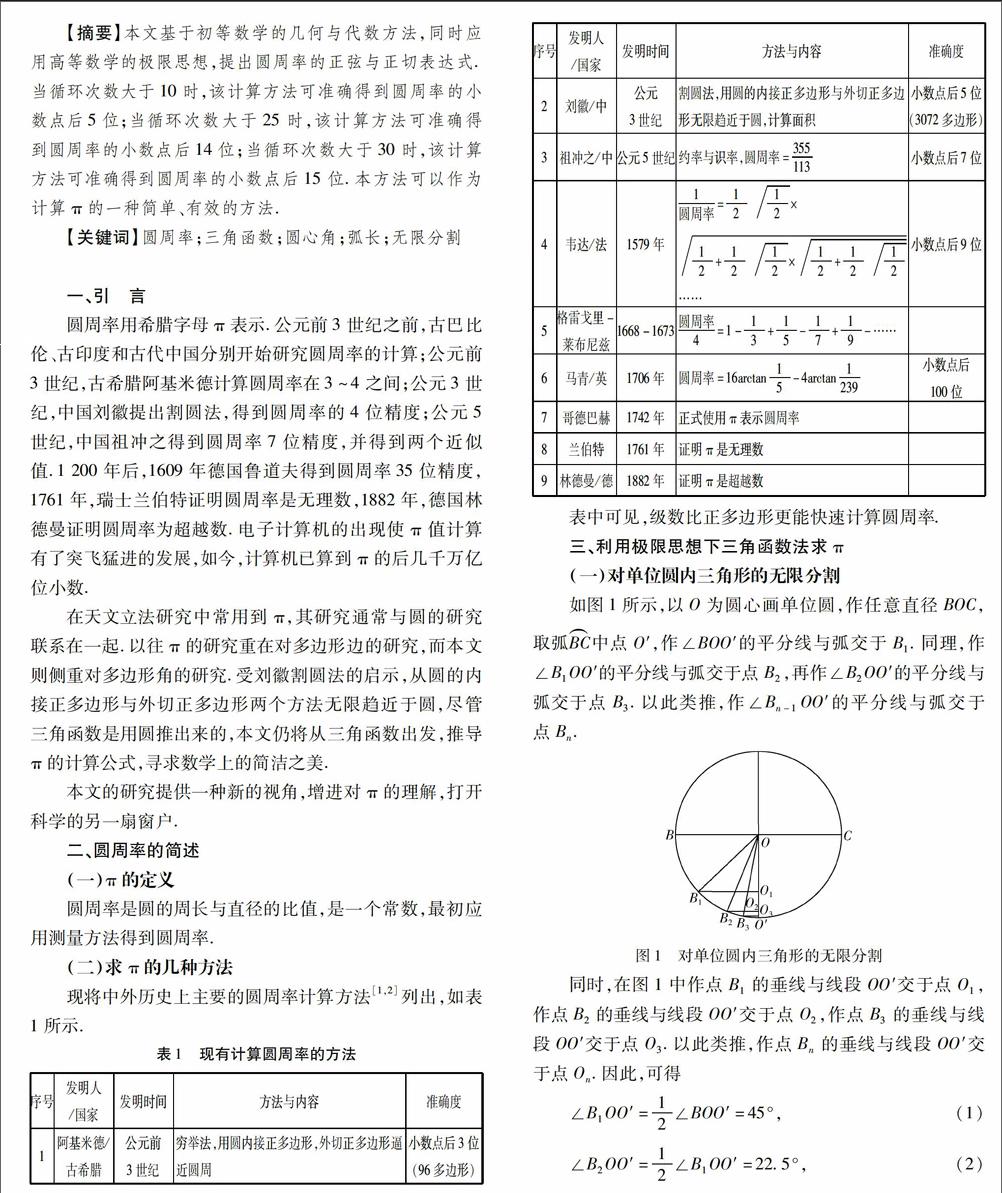
在天文立法研究中常用到π,其研究通常与圆的研究联系在一起.以往π的研究重在对多边形边的研究,而本文则侧重对多边形角的研究.受刘徽割圓法的启示,从圆的内接正多边形与外切正多边形两个方法无限趋近于圆,尽管三角函数是用圆推出来的,本文仍将从三角函数出发,推导π的计算公式,寻求数学上的简洁之美.
