弧长和扇形面积公式教学设计

兰标超

一、内容和内容解析

（一）内容

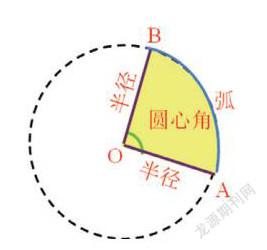
弧长和扇形面积公式

（二）内容解析

弧长和扇形面积公式是与圆有关的计算中的两个常用公式，应用弧长和扇形面积公式可以计算一些与圆有关的图形的周长和面积，也可以解决一些简单的实际问题.学习这两个公式也为圆锥侧面积公式的推导打下了基础.

弧长公式是在等分圆周和圆周长公式的基础上，借助部分与整体之间的联系推导出来，运用相同的方法，可以在圆面积公式的基础上推导出扇形面积公式，进而通过弧长公式表示扇形面积.

基于以上分析，确定本节课的教学重点是：弧长和面积公式的推导及运用.

二、目标和目标解析

（一）目标

1.以圆的周长和面积为基础，探究弧长和扇形的面积公式，并会用来计算弧长和扇形面积.

2.体会类比、转换的数学思想.

（二）目标解析

达成目标1的标志是：学生能够理解10的圆心角所对的弧长等于圆周长的对的扇形面积等于圆面积的;能够发现n0的圆心角所对的弧长和扇形面积都是10的圆心角所对的弧长和扇形面积的n倍;能够利用弧长表示扇形面积，并能利用公式计算弧长和扇形面积.

达成目标2的標志是：在弧长和扇形面积公式的推导过程中，发现弧长与圆周长、扇形面积与圆面积都是部分与整体之间的关系，从而将计算弧长和扇形面积的问题转化为求圆周长和圆面积的一部分来解决，体会转化、类比的数学思想

三、教学问题诊断分析

对于“10的圆心角所对的弧长等于圆周长的”，有些学生觉得有些抽象，难以把等分弧与等分3600角联系起来。因此公式的推导过程设计应围绕着如何突破这个难点。

基于以上分析，本节课的教学难点是：推导弧长和扇形面积公式的过程。

教学过程设计：

问题引入：数学来源于生活，在我们日常生活中，弧形随处可见，大到星体运行轨道，小到水管弯管，操场跑道，高速立交的环形入口等等，你有没有想过，这些弧形的长度怎么计算呢？请大家再观察扇面，这节课我们就一起探讨与扇形有关的一些几何量.

设计意图：激发学生的学习兴趣，引发学生的数学思考.让学生体验从实际背景中抽象出数学问题、寻求结果、解决问题的过程。

温故知新：复习“圆弧”的概念.

老师提问：圆的周长是否可以看作弧长？若可以，它应看成多少度的圆心角所对的弧长？

设计意图：让学生加深对“弧长是圆周长的一部分”“圆周长可以看作360°的圆心角所对的弧长”的理解，为下一步用“部分”与“整体”的关系推导弧长公式做铺垫.

1.推导并应用弧长公式

问题1：试计算下图中各段弧长，并总结弧长计算公式.

归纳：弧长计算公式是：

设计意图：理解了弧长是圆周长的一部分后，先让学生计算180°，90°，60°这些特殊圆心角所对的弧长，其实就是让学生在数学实践中理解“具体的一段弧长占所在圆周长的几分之几”的问题，进而发现计算规律.如果学生没发现计算规律，教师再启发学生思考同圆或等圆中1°的圆心角所对的弧长与n°的圆心角所对的弧长有何数量关系，最后总结弧长计算公式.

教师提问：我们是如何推导弧长公式的？

学生回答：在同圆或等圆中， 先1°的圆心角所对的弧长，再求n °的圆心角所对的弧长.

设计意图：尝试回顾解决问题的过程，培养学生总结数学经验，养成乐于思考的良好品质，体会数学的基本思想和思维方式.

教师提醒：弧长公式中n和180习惯上是不带单位的.

设计意图：提醒学生在以后的解题中要注意数学书写的规范性.

例1：制造弯形管道时，经常要先按中心线计算“展直长度”，再下料，已知图中∠AOB=100°，试计算图

设计意图：通过实际问题，加深学生对弧长公式的认识，同时让学生体会数学与生活生产息息相关，数学广泛应用于社会生产和生活的各个方面

师生活动：让学生独立完成，并让学生代表展示解题结果.

设计意图：（1）了解、评价学生学习弧长公式的过程和结果;

（2）培养学生独立思考的能力，在运用数学知识和方法解决问题的过程中，认识数学的价值.

（3）让学生感受成功的快乐，体验独自克服困难、解决数学问题的过程，有克服困难的勇气，具备学好数学得信心.

2.推导扇形面积公式

师生活动：（出示图）介绍扇形的定义。

教师师：强调扇形是面，对于面数学中往往考虑如何求它的面积。

教师提问：同学们已经认识了扇形.你能否类比刚才我们研究弧长公式的方法推导出扇形面积的计算公式？（学生在学案上完成任务，并让学生代表展示学习成果）

设计意图：（1）让学生再次理解局部和整体的关系，培养学生独立思考的能力，体会类比、转化的数学思想，能针对他人所提出的问题进行反思，经历借助图形思考问题的过程，掌握分析问题和解决问题的一些基本数学思想方法.

（2）让学生积极参与数学活动，对数学有好奇心和求知欲，敢于发表自己的想法，养成勤奋、合作交流等学习习惯，形成严谨求实的科学态度.

教师提问： 比较弧长与扇形面积公式，你能用弧长表示扇形面积吗？试一试！

师生活动：教师引导。在得出扇形的另一个计算公式之后，教师可以引导学生，这个公式与三角形的面积公式类似，只要把扇形看作一个曲边三角形，把弧长l看成底，半径R看成高就可以了。

设计意图：通过比较弧长和扇形面积公式，让学生发现可以通过弧长表示扇形面积，为圆锥曲侧面积公式的推导作准备。

例2;如图，已知☉O的半径是6cm，∠AOB=120°试求阴影部分面积.

（学生在学案上完成，学生代表展示解题结果）

设计意图：加深学生对扇形面积公式的认识，培养学生养成认真勤奋、独立思考的学习习惯，形成严谨的科学态度。

2.课堂小结

（1）弧长和扇形面积公式是什么？你是如何得到这两个公式的？如何运用？（2）弧长与圆周长、扇形面积与圆面积之间有什么联系？

设计意图：通过小结梳理本节课所学内容，把我本节课的核心——弧长和扇形面积公式，并体会部分与整体之间的联系和类比、转化的数学思想.

2.布置作业：习题24.4  1（1）（2），4，6，8.

设计意图：考查学生对本节课学习目标完成效果.

课后教学反思：

本节课的内容一般来说老师会把重点放在公式的理解和熟练运用上，对于九年级的学生来说这很重要，而且弧长公式和扇形面积公式的推导过程也比较容易理解。但是这样可能导致中等及以下学生因为某些概念、细节的不理解或者不懂，造成学习的障碍。结合学生的实际，分析学生可能出现障碍的地方，逐步引导学生观察、比较，从基本的概念入手，处理好各个思维的转折点，在注重基础的同时发展学生的数学能力，关注了全体学生的发展。

针对学生的实际情况，在课堂中关注大多数学生能够参与到教学中来很重要，存在的不足之处是，于九年级的学生来说，成绩较好学生的思维明显受到限制，不能最大限度地培养数学优生的数学思维。如何在关注全体学生的同时让优生最大限度的发展，最终体现课程标准中让不同的人在数学上得到不同的发展的理念，是我们数学课堂教学一直要思考的问题。本堂课的不足还在于时间的分配上不是很合理，由于在学生在探索弧长时我担心引导措施不到位，导致时间过长，后面的教学环节比较吃紧，对学生在新知的应用上没有足够的时间。有待于在今后的教学中注意这方面的问题，以便进一步提高课堂教学效率.

参考文献：

[1]韩美艳.“弧长和扇形面积”教学设计[J]. 中小学数学：初中版， 2017（5）：3.