斜齿轮系统多自由度耦合模型及非线性因素表征

程联社，陈润霖

（1.杨凌职业技术学院机电工程学院，陕西 杨凌712100；2.西安交通大学机械工程学院，陕西 西安710049）

0 引言

斜齿轮传动的重合度大，提高了齿轮的承载能力，工作平稳性好，噪音小，在对性能要求较高的场合已经全面取代了直齿轮，如工程机械、冶金、采矿、食品工业及航空航天等领域［1］。但是结构上斜齿轮引入了螺旋角因素，从单自由度振动拓展为多自由度振动，包括齿轮的扭振、横向弯曲振动、轴向振动和齿轮体的圆盘振动等［2］，加上齿轮传动的诸多非线性因素，使得斜齿轮系统动力学行为更为复杂，这就需要对斜齿轮传动系统动力学模型进行深入的分析，以利设计。完整的传动系统模型是以齿轮系统中的传动系统作为分析对象，包含齿轮副，传动轴，也可以包含支承轴承、原动机和负载的惯性［3－7］。

1 斜齿轮弯－扭－轴耦合振动模型建立

1对相啮合的斜齿轮如图1所示。其中，Oa和Op分别为主、从动斜齿轮的中心；F为2个齿轮的啮合力；kn为轮齿啮合刚度；cn为啮合阻尼；kay，kaz，cay，caz分别为主动轮的径向和轴向的支承刚度、阻尼；kpy，kpz，cpy，cpz分别为从动轮的径向和轴向的支承刚度、阻尼。

图1 斜齿轮弯－扭－轴耦合分析模型

该斜齿轮系统为一个6自由度系统，根据牛顿运动定律，设其广义位移列阵为：

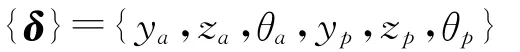
yi，zi，θi（i＝a，p）分别为主动轮和从动轮的中心点在切向（y向）、轴向（z向）的平移振动位移和绕轴向（z向）的扭转振动位移。Ii（i＝a，p）分别为主、从动齿轮绕其轴线的转动惯量；Ti（i＝a，p）分别为作用在主、从动齿轮的外载荷力矩。

将切向和轴向动态力代入上式中，把上面的方程写成矩阵形式，即得到斜齿轮系统的动力学模型为：

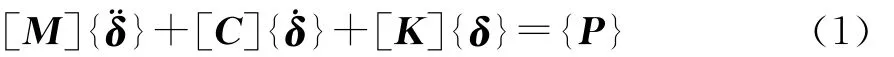
［M］为质量矩阵；［C］为阻尼矩阵；［K］为刚度矩阵；［P］为外激励向量。

2 斜齿轮弯－扭－轴耦合系统振动分析

2.1 固有频率和振型

对于式（1），不考虑轮齿误差e和各种阻尼c，令P＝0，采用模态分析法［2］可得：

令［A］＝［M］－1［K］，则矩阵［A］6个特征值的平方根（ω1，ω2，ω3，ω4，ω5，ω6）即为斜齿轮系统的各阶固有圆频率，其对应的特征向量即为对应的主振型。针对某斜齿轮传动系统，各参数数值如表1所示。

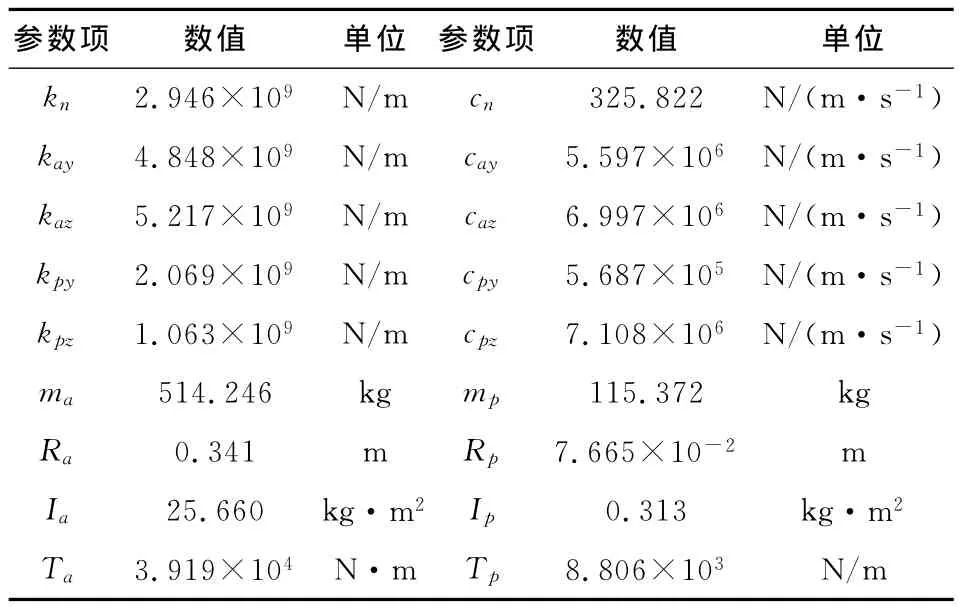
表1 振动模型中各参数数值

把各参数代入式（1）中，不考虑阻尼和轮齿误差e，通过编程求解得到系统的各阶固有频率分别为：f1＝0Hz，f2＝455Hz，f3＝573Hz，f4＝726Hz，f5＝1 047Hz，f6＝2 843Hz。

其对应的主振型分别为：

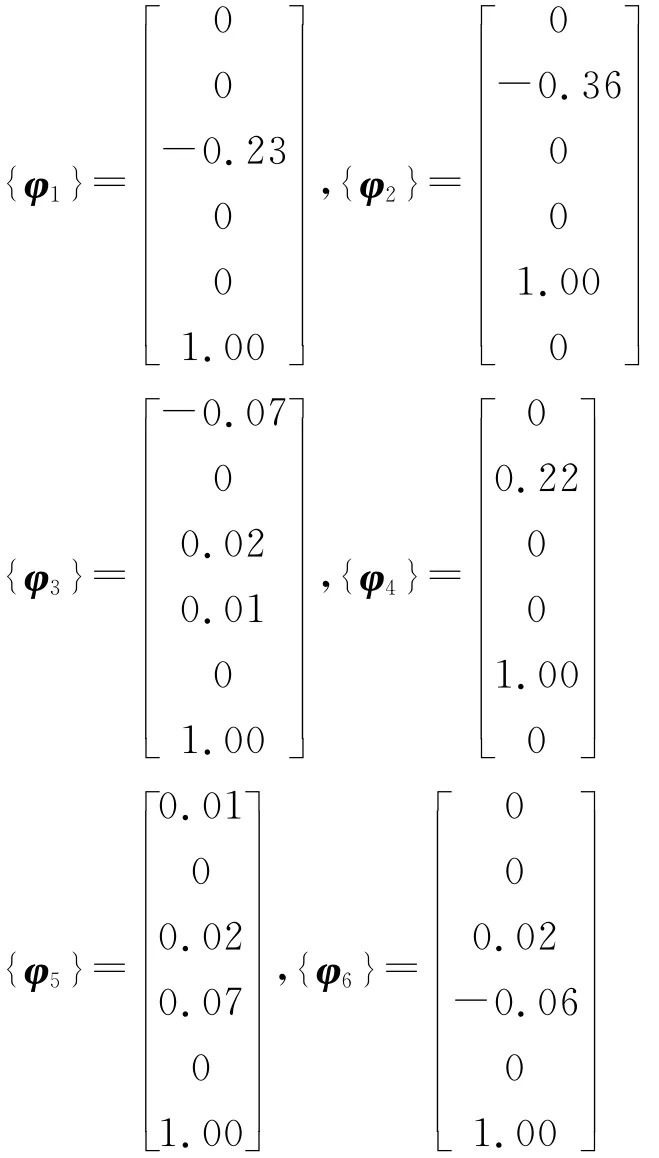
对于上述6个振型，1阶振型为斜齿轮的刚体振型，2～6阶振型为弹性振动的振型。其中，2阶振型为轴向振动，最大振动为从动轮的轴向振动；3阶振型为径向和扭转振动，最大振动为从动轮的扭转振动；4阶振型为轴向振动，最大振动为从动轮的轴向振动；5阶振型为径向和扭转振动，最大振动为动轮的扭转；6阶振型为径向和扭转振动，最大振动为从动轮的扭转振动。

2.2 耦合振动响应分析

假定在t＝0时刻，系统的初始位移和初始速度分别为：

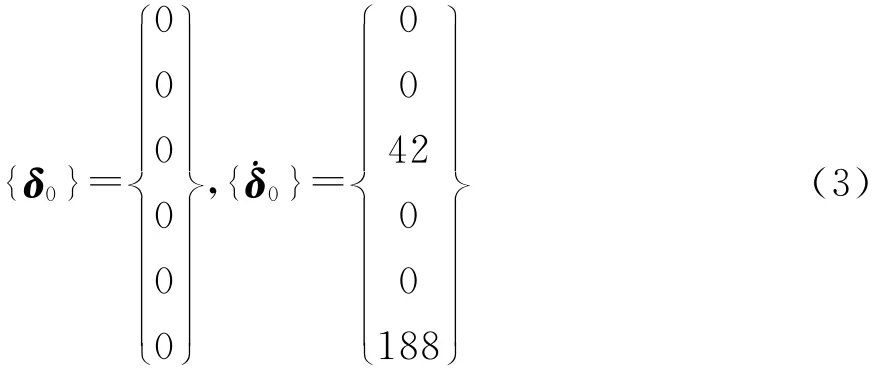
在不考虑阻尼的条件下，采用振型叠加法，求得系统的振动时域关系。相比较而言，斜齿轮副的主、从动轮的径向振动位移都较大，分别为0.747mm和0.633mm，而轴向振动位移都比较小。对于扭转振动，从动轮的扭转振动情况比较严重，在齿顶的振动位移达到了1.738mm，主动轮的扭转振动则要小得多，齿顶的振动位移大约0.129mm。

3 斜齿轮传动非线性因素分析

3.1 时变刚度的表征分析

在斜齿轮啮合过程中，轮齿啮合的接触线是倾斜的，且同时啮合的轮齿对数较多（一般≥3），为了简化起见，假设载荷在接触线长度方向上均匀分布，这就可以用齿轮副接触线长度的变化代替瞬时啮合刚度的变化，来求解一对斜齿轮副的时变啮合刚度。

如图2所示，平面ABCD为一对斜齿轮的啮合平面。AD＝εα·Pb（Pb为基圆齿距）；AB＝CD＝b（b为斜齿轮副的齿宽）；BE，DF等均为齿轮副的啮合接触线；βb为齿轮副的基圆螺旋角；εα，εβ分别为斜齿轮副的端面和轴向重合度。

于是，一对相啮合的轮齿接触线长度的变化曲线如图3所示。

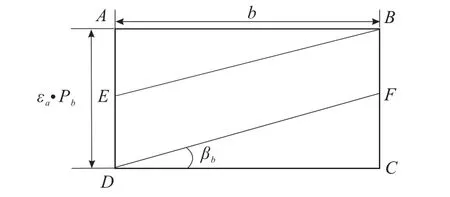
图2 斜齿轮啮合平面

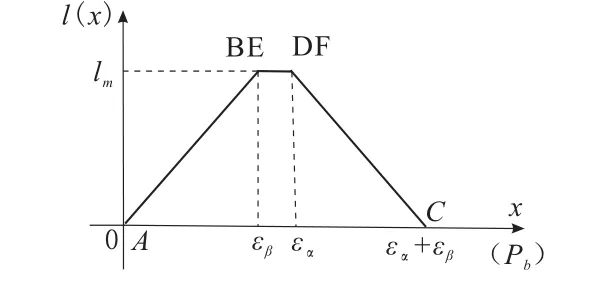
图3 一对轮齿接触线长度变化曲线

故接触线长度函数的表达式为：

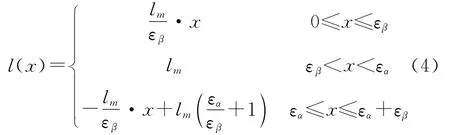
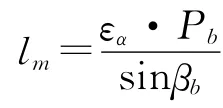
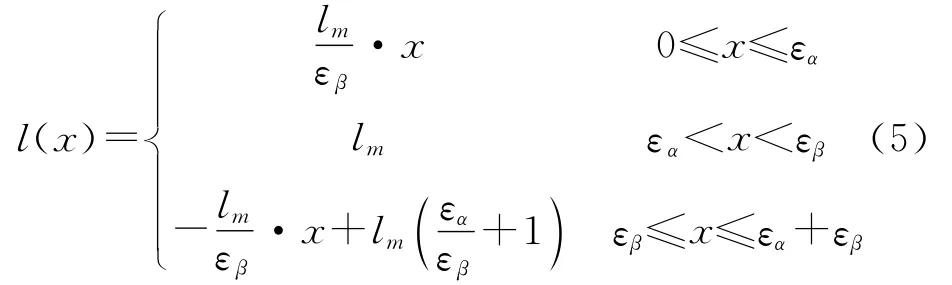
由于斜齿轮副的总重合度大于1，则总存在多对轮齿的接触，它们共同分担载荷。由于系统研究的斜齿轮副重合度大于2，所以至少有2对轮齿接触，在实际啮合过程中接触线的总长度即为这几条接触线长度之和，如图4所示。

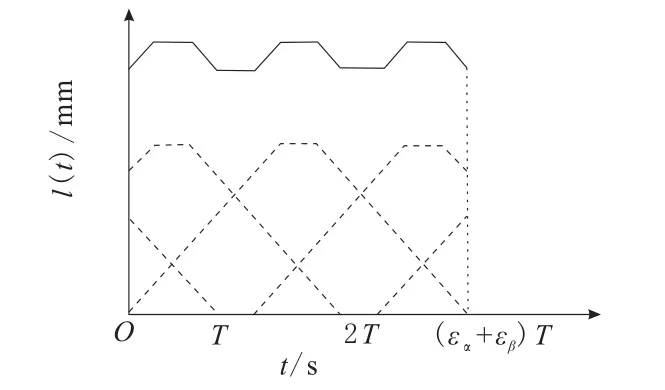
图4 多对轮齿啮合的接触线总长度随时间变化曲线

根据前面的假设，设斜齿轮副动态啮合刚度与接触线之间的关系为：

kl为刚度与接触线之间转化的一个系数。若km为斜齿轮副的平均啮合刚度［8］，la为一个周期内接触线的平均长度，则kl＝km／la。

于是，在1个周期T（T＝60／（n1z1））内，斜齿轮刚度变化曲线如图5所示。其中，n1，z1分别为主动轮的转速和齿数。

把刚度随时间变化的函数用傅里叶级数展开，并针对某斜齿轮传动系统，通过编程计算得该齿轮副的时变啮合刚度曲线及各阶傅里叶展开曲线如图6所示。

通过对比可知，前5阶傅里叶级数展开的曲线与原时变刚度曲线基本吻合，其精度可以满足一般计算的要求，可以采用前5阶傅里叶展开式来代替原时变刚度的分段函数，即

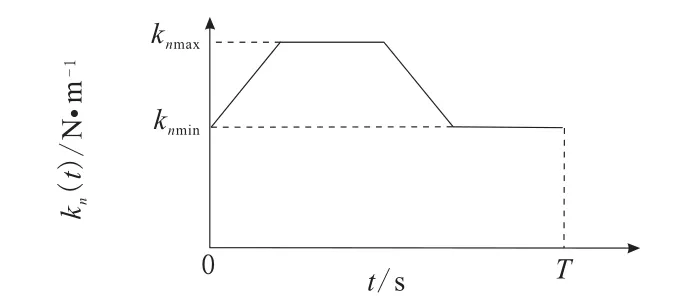
图5 1周期内刚度变化曲线

图6 斜齿轮刚度曲线及1，3，5阶傅里叶展开曲线

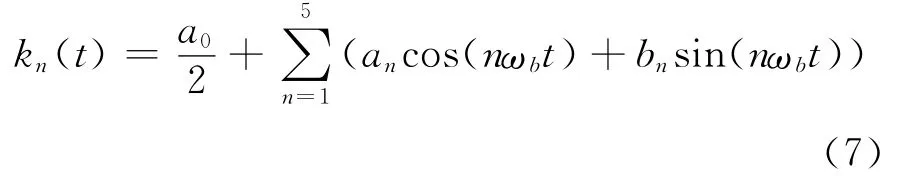
an，bn为傅里叶系数，ωb＝2π／T。在代入非线性动力学模型中时，需先计算确定系数an，bn和ωb。对于所研究的某斜齿轮传动系统，系数如表2所示。

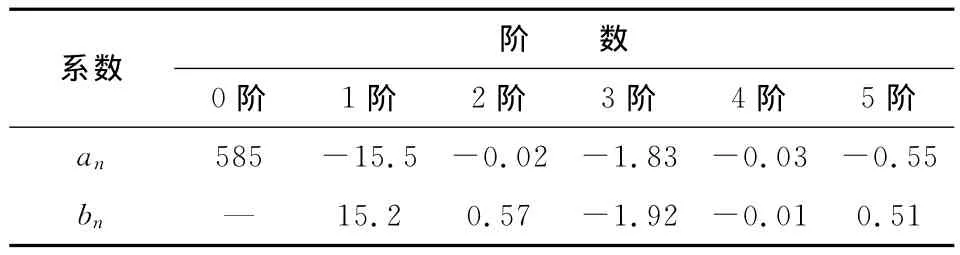
表2 时变刚度表达式中的系数（×107） N／m

3.2 齿侧间隙的表征分析

设函数f为描述具有齿侧间隙时轮齿啮合力的非解析函数［8］，若将其处理成对称形式，则其表达式为：

c为齿侧间隙。

间隙函数的曲线如图7所示。在［－k，k］范围内用高次多项式进行拟合，结果如图8和图9所示。

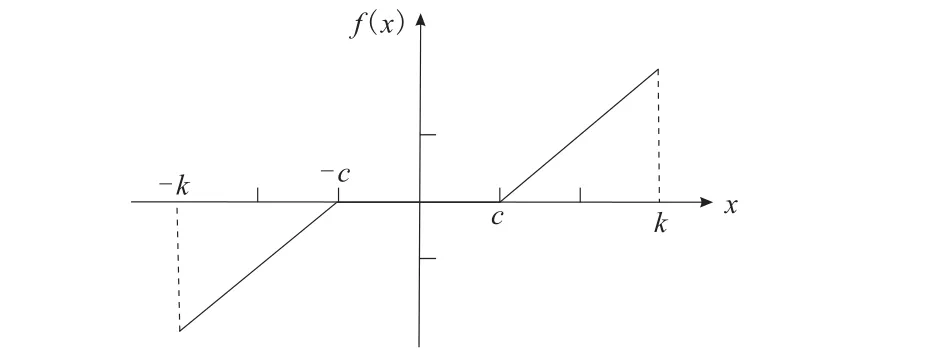
图7 齿侧间隙描述函数

图8 齿侧间隙函数及1，3，5阶拟合曲线

图9 齿侧间隙函数及5，7，9阶拟合曲线

对比图8，图9，可知多项式的次数取的越高，拟合的精度也就越高，但是当次数高于7次以后，多项式次数的提高对拟合精度的提高已经不明显了。实际上，3次多项式已经能够反映齿侧间隙描述函数的总体变化趋势，所以为了之后分析的方便，可以用3次多项式来拟合齿侧间隙描述函数，即

对所研究的某斜齿轮传动系统，齿侧间隙为c＝5×10－5m，取k＝2×10－4m，可得a1＝0.344，a3＝1.201×107。

4 结束语

通过振型分析可知，所研究的斜齿轮副的扭转振动比径向振动和轴向振动大得多，需重点考虑。并分析了2种非线性因素，采用接触线长度等效的简化算法给出了时变刚度的表达式；基于“振－冲”模型给出了齿侧间隙的表达方法。这些为齿轮系统非线性动力学分析提供了依据。

［1］ 唐定国，陈立民.齿轮传动技术的现状和展望［J］.机械工程学报，1993，20（3）：35－41.

［2］ 李润方，王建军.齿轮系统动力学［M］.北京：科学出版社，1997.

［3］ 苏武会，李育锡.斜齿轮转子系统弯扭耦合振动分析的整体传递矩阵法［J］.机床与液压，2007，35（6）：38－41.

［4］ 楼建勇，林 江.斜齿轮传动装置动力学模型的建立及动特性研究［J］.浙江工业大学学报，1998，26（1）：83－88.

［5］ 王立华，李润方，林腾蛟，等.齿轮系统时变刚度和间隙非线性振动特性研究［J］.中国机械工程，2003，14（13）：1143－1148.

［6］ 李瑰贤，马 亮，林少芬.宽斜齿轮副啮合刚度计算及扭振特性的研究［J］.南京理工大学学报，2002，26（1）：35－39.

［7］ 王玉新，柳 杨，王仪明.考虑啮合时变刚度和传递误差的齿轮振动分析［J］.机械传动，2002，26（1）：5－8.

［8］ GB／T 3480－1997.渐开线圆柱齿轮承载能力计算方法［S］.