基于模型预测控制的阵风减缓技术研究

刘岳锋，白俊强，孙智伟

（西北工业大学航空学院，陕西 西安710072）

0 引言

阵风减缓是主动控制技术的重要组成部分，在现代飞机设计中得到了越来越广泛的应用。它能有效地降低阵风引起的附加过载，改善飞行品质并提高结构的疲劳寿命。传统PID控制、线性二次高斯控制（LQG）和鲁棒性控制（H∞）等都在阵风减缓控制中得到了应用，并取得较好效果［1］。但实际系统都存在舵偏角和舵偏速率等约束，上述方法均难以处理系统存在约束的情况。

模型预测控制（MPC）是20世纪70年代产生于工业过程控制领域的一类计算机控制算法。MPC基于滚动优化，通过在线求解二次规划（QP）问题，得到每一采样时刻满足系统约束的最优控制输入。MPC的特点是滚动优化，滚动实施，具有一定的自适应性，因此，MPC非常适合状态和输入存在约束的非线性或时变系统。但由于每一采样时刻都需求解QP问题，MPC存在计算量大的缺陷［2］。随着计算机软硬件水平的不断发展以及高效可靠QP算法的出现，使MPC应用到诸如航空航天和机器人等实时性要求较高的控制领域成为可能［3－6］。

1 模型构造

1.1 阵风模型

飞机过载增量主要由垂直阵风引起，而水平阵风的影响较小，因此，设计阵风减缓系统时着重考虑垂直阵风的影响［7］。

系统使用离散和连续阵风模型进行控制律设计和仿真。对于离散阵风，一般采用（1－cos）阵风模型，具体形式为：

wg为垂直阵风速度为阵风强度；Lg为阵风尺度。

对于连续阵风模型，由于仅针对刚性飞机进行阵风减缓研究，只需要考虑低频范围的阵风。在低频范围内，Dryden模型和Von Karman模型基本一致［8］。因此，采用结构形式更为简单的Dryden模型。

Dryden函数谱为有理谱，根据有理谱成形理论，可以认为连续阵风wg是以单位强度白噪声w为输入的一个线性成型滤波器的输出。由此可得到连续阵风的线性化模型为：

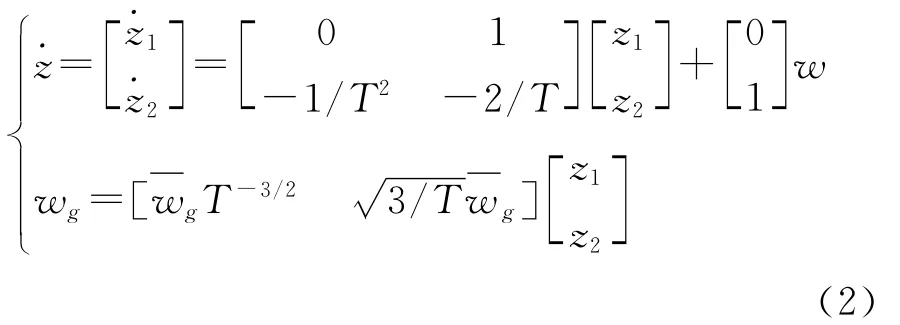
T为风干扰的特征长度L与航迹速度V0的比值。

1.2 飞机－阵风模型

飞机的动力学特性是通过六自由度方程来描述的，但是六自由度方程为非线性方程，并且存在纵向和横航向耦合，不便于进行控制律设计。通过小扰动假设，标准的六自由度方程被线化和解耦，从而得到线化的纵向小扰动方程。此外，垂直阵风wg引起迎角增量Δαg，相当于在飞机运动方程中引入了Δαg的干扰，它对飞机运动的影响即是对迎角α的影响［9］。因此，结合飞机纵向小扰动方程和阵风的线性化模型，可建立如下状态空间方程，即

其中

Δυ，Δα，Δq，Δθ分别为航迹速度、迎角、俯仰角速率和俯仰角的增量；Δnz为法向过载增量；δe和δf分别为升降舵和襟翼偏角；v代表输出量的随机扰动，为零均值的Gauss白噪声。

2 模型预测控制

2.1 预测模型

MPC是一种基于模型的控制算法，对于MPC来讲，只注重模型的功能，而不注重模型的形式。预测控制的功能就是根据对象的历史信息和未来输入，预测未来输出。因此，预测控制具有展示未来动态行为的能力。

对于式（3）所示状态空间模型，预测模型具体形式为：

x（k＋j｜k）为k时刻对k＋j时刻状态量的预测值；x（k）为k时刻状态量；u（k＋j｜k）为k时刻对未来k＋j时刻控制输入的预测值。

2.2 滚动优化

在MPC中，通常优化不是一次离线进行，而是反复在线运行。即在每一采样时刻，优化性能指标通常只涉及未来的有限时间，而到下一采样时刻，这一优化时域向前推移。这是滚动优化的含义，也是MPC区别于传统最优控制的根本特点。优化的滚动实施能应对由于模型失配、约束和干扰等引起的不确定性，及时进行弥补，始终把最新的优化建立在实际的基础上，使控制保持实际上的最优。

2.3 控制器求解

由于MPC为离散控制方法，故需要使用离散的状态空间方程。对于式（3）所示被控系统，选择二次性能函数作为优化目标，式（5）给出了二次性能函数的一般形式，即

xk，xref，k和uk分别为k 时刻状态变量，参考状态变量以及控制信号；向量U为控制时域Nu的控制信号序列；Np为预测时域，预测时域要比控制时域长；矩阵Q和R为状态变量以及控制量的权重矩阵；Qf为终端加权矩阵。

预测状态变量序列可以通过未来输入序列U和当前状态变量xk表示，形式为：

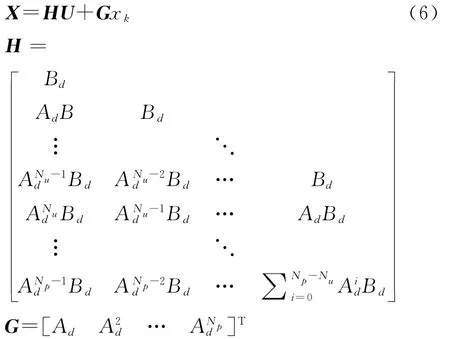
由于缺乏完整的状态信息（部分状态变量不可测量或难以测量），必须使用当前状态的估计值＾xk来代替式（5）中的xk。＾xk可以通过最优估计器来获取，系统采用Kalman滤波器作为估计器。

为了更真实地反应物理系统的实际特性，避免不可实现的控制输入，在当前研究中引入舵面偏角约束。因此，式（5）所示问题转化为带约束的优化问题，具体形式为：

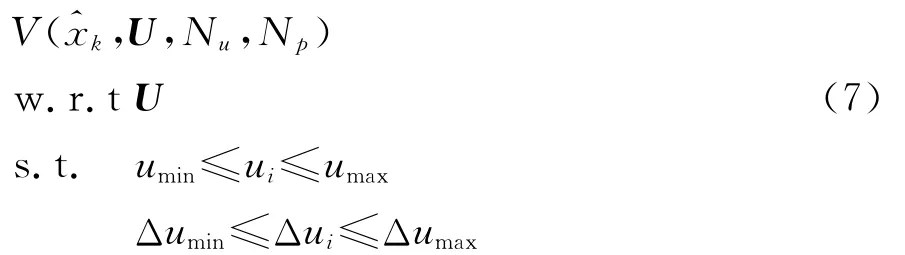
式（7）不等式约束可以转换为紧凑的矩阵形式FU≤c，其中，F，c分别为：

对未来输出预测序列以及不等式约束使用紧凑形式表达，可以将二次性能指标转化为：

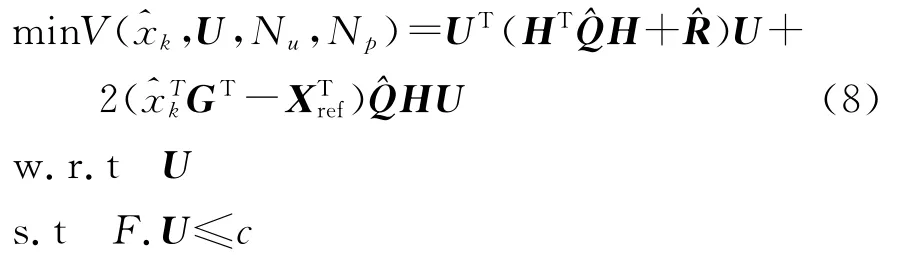
Xref为整个预测时域的参考状态变量序列，＾Q，＾R为块对角矩阵，可以表示为：Q＝diag［Q Q …Qf］，R＝diag［R R … R］。

式（8）为典型二次规划问题，对于正定权重矩阵Q，可以知道矩阵HT＾Q＾H 同样为正定矩阵，因此，式（8）实际为一个凸二次规划问题。对于此类问题，最优解存在且唯一。参考文献［10］提供了一种高效的凸优化算法，能够快速求得最优控制输入。MPC控制系统的工作原理如图1所示。

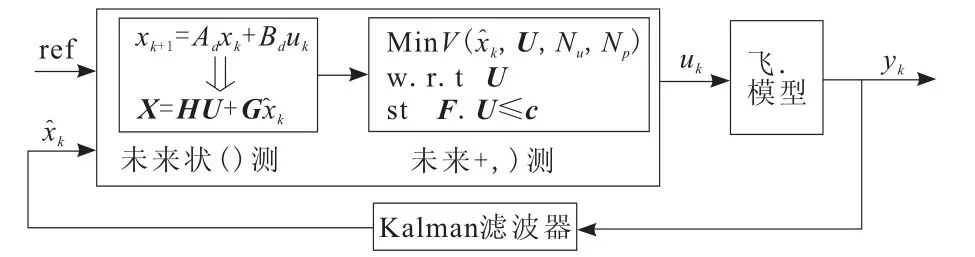
图1 MPC系统原理

2.4 模型预测控制器稳定性分析

如果一个系统可镇定和可检测，那么标准LQ无限时域控制方法可以构造一个稳定优化控制器。然而，MPC为有限时域控制器，一个以二次性能指标为基础的有限时域控制器通常并不能保证渐近稳定。使用有限时域控制，是为了数值处理更容易，但是也可能造成系统不稳定。为了保证MPC的稳定性，近年来发展了许多稳定性 MPC算法［11－12］。如果（A，B）是可镇定的；（A，Q1／2）可观的；且性能指标函数满足单调性条件，即V（xk，U＊，N＋1）≤V（xk，U＊，N），则MPC控制器是稳定的。

应用以下任何一类终端条件，约束MPC单调性即可满足：终端等式约束；终端约束集；终端代价函数。前2种方法会减小可行域，特别是终端等式约束。系统采用终端代价函数方法。当终端代价函数满足式（9），可以保证性能指标函数满足单调性条件［11］，即

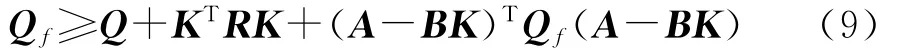
K为线性二次调节器（LQR）增益（LQR选取与MPC一致的Q，R权重矩阵）。

根据矩阵的schur补性质，式（9）可以转化为线性矩阵不等式（LMI）形式，从而可以方便求出2］。LMI形式为：

3 Kalman滤波器

在飞机纵向运动的4个主要状态变量中，只有俯仰角速度和俯仰角的测量精度较高可直接利用，而迎角和航迹速度的测量结果，由于受到诸多因素的影响而不能直接用于控制系统，所以一般用迎角和航迹速度的最优估计值代替，组成状态反馈矩阵［13］。

对于式（3）描述的系统，状态估计值可以通过Kalman滤波器来获得，即

L（k）的求解需要给定输入干扰协方差矩阵Qn，测量噪声协方差矩阵Rn和输入输出协方差矩阵Nn。利用＾x（k）代替x（k），即可与 MPC控制器联合求解。

4 仿真分析

4.1 模型描述

为了验证MPC算法的性能，将阵风减缓控制器应用于某大型飞机，并针对系统无约束和有约束情况，分别与LQG控制器进行对比仿真计算。给定阵风强度为5m／s，飞行速度为200m／s。飞机展长为44.8m，机身长为54.1m，机翼面积为260 m2，平均气动弦长为6.6m，巡航质量为130 000 kg。

4.2 仿真结果及分析

MPC控制器性能取决于权重矩阵，预测时域和控制时域的长度。其中，控制时域的选择需要通过反复试验，一般而言控制时域越长，控制性能越好，但计算量也越大。MPC控制器参数如表1所示。

表1 MPC控制器参数

图2～图3给出了飞机在1－cos阵风下，2种控制方法的仿真结果。结果比较了在有约束和无约束2种情况下，系统的过载响应。仿真结果表明，在无约束时，MPC和LQG减缓效果基本一致；有约束时，MPC的舵面响应更快，更早进入舵面饱和状态，因而对于系统约束具有更强的适应性。

图2 无约束过载响应（1－cos阵风）

图3 有约束过载响应（1－cos阵风）

图4～图5给出了飞机在连续Dryden阵风下，2种控制方法的仿真结果。相比LQG控制器，MPC控制器在系统存在约束时，具有更强的适应性和更好的性能。

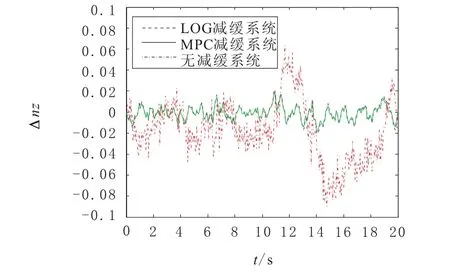
图4 无约束过载响应（Dryden阵风）

图5 有约束过载响应（Dryden阵风）

MPC和LQG控制器的阵风减缓率如表2所示。

表2 阵风减缓率 %

从表2可看出，离散阵风减缓率大于连续阵风减缓率；无约束减缓率大于有约束减缓率；有约束时，MPC控制器减缓率大于LQG控制器。

连续阵风下控制系统所消耗的计算时间如表3所示。

表3 控制器计算时间 s

其中，计算机主频为2.67GHz，单核运算，仿真时间为20s，采样步长为0.05s。从表3中可知，LQG为无穷时域离线控制器，其计算效率高于在线的MPC控制器；有约束比无约束计算效率低；且预测时域越长，计算效率越低；所有计算时间远小于实际仿真时间，不会导致控制器延迟，计算效率可以满足工程需要。

5 结束语

通过小扰动假设获得飞机动力学模型，并与阵风模型结合得到飞机－阵风状态空间方程。在系统状态空间方程基础上进行控制律设计和仿真计算，得出以下结论：

a.当系统不存在约束时，MPC实质就是有限时域的LQG算法，因而此时MPC阵风减缓率与LQG减缓率基本一致。

b.系统存在约束时，MPC采用滚动优化策略，每一时刻进行最优二次规划求解，能够获得满足约束条件的最优控制；而LQG是属于一次离线优化，不能在优化中考虑约束的影响。因此，在约束条件下，MPC控制性能优于LQG算法。

c.MPC算法采用滚动在线优化，计算效率低于LQG；MPC预测时域越长效率越低，且有约束比无约束效率低，但MPC计算效率能够满足工程需要。

［1］ 粱苏南，王立新，张曙光.飞机风载荷减缓控制技术及其发展［J］.飞行力学，2003，21（1）：1－4.

［2］ 邹 涛，丁宝苍，张 端.模型预测控制工程应用导论［M］.北京：化学工业出版社，2010.

［3］ Kim H J，Shim D H，Sastry S.Nonlinear model predictive tracking control for rotorcraft－based unmanned aerial vehicles［J］.American Control Conference，2002，（5）：3576－3581.

［4］ Kang Y，Hedrick J K.Design of nonlinear model predictive controller for a small fixed－wing unmanned aerial vehicle［C］.AIAA Guidance，Navigation and Control Conference and Exhibit.Colorado，Keystone，2006.

［5］ 华思亮，陈宗基，袁利平.基于模型预测控制的无人机编队自主重构研究［J］.系统仿真学报，2009，（20）：383－386.

［6］ 吴成富，冯 乐，隋 丹，等.模型预测控制算法在飞机自动着陆控制系统中的应用［J］.西北工业大学学报，2004，22（2）：140－144.

［7］ 张军红，李振水，詹孟权，等.LQG控制理论在阵风载荷减缓系统中的应用［J］.飞行力学，2007，25（2）：61－64.

［8］ 肖业伦，金长江.大气扰动中的飞行原理［M］.北京：国防工业出版社，1993.

［9］ 文传源.现代飞行控制［M］.北京：北京航空航天大学出版社，2004.

［10］ Boyd S，Vandenberghe L.Convex optimization［M］.Cambridge：Cambridge University Press，2004.

［11］ Kwon W H，Han S.Receding horizon control：model predictive control for state models［M］.London：LVerlag London L；mieed Springer，2005.

［12］ Batina I.Model predictive control for stochastic systems by randomized algorithms［D］.Proefschrift：Technische Universiteit Eindhoven，2004.

［13］ Gangsaas D，Ly U，Norman D C.Practical gust load alleviation and flutter suppression control laws based on a LQG methodology［R］.Washington：Boeing Commercial Airplane Company，1981.