基于齐次量纲雅可比矩阵的四自由度并联机构运动灵巧度分析

姜子强，李永刚，许立新

（天津职业技术师范大学机械工程学院，天津300222）

0 引言

基于雅可比矩阵的运动学尺度综合是并联机构的主要设计任务之一。但对于输出运动是平移运动和转动运动相耦合的机构，其雅可比矩阵存在量纲不一致的问题，致使其不能直接应用于机构的运动灵巧度分析。

雅可比矩阵对于奇异性分析、刚度矩阵的建立和运动尺度综合具有重要的意义［1－5］。因此，雅克比矩阵的构造一直是机构学领域的研究热点之一［2，6－9］。少自由度并联机构的完整雅克比矩阵通常为6×6矩阵，其中，完整雅克比矩阵包括约束子矩阵和运动子矩阵［2，6］。Joshi［3］利用螺旋理论给出了对称并联机构的完整雅可比矩阵的建模方法。李永刚［4］等利用该方法分析了非对称机构的雅可比矩阵的求解方法。但是此类雅可比矩阵存在量纲不一致的问题。为此，一种基于数值算法的齐次雅可比矩阵被提出用于尺度综合和运动灵巧度分析［7－8］。随后，Liu［9］等又给出一种解析方法，并用若干中对称机构进行了实例分析。

借助以上方法，构造出了非对称并联机构2RRS－2RUS的齐次量纲完整雅克比分析。通过求解齐次量纲雅克比矩阵的条件数的分布规律，对经过归一化处理的机构尺度参数，进行了性能参数随各尺度参数的变化规律。

1 2RUS－2RRS并联机构

如图1所示，并联机器人主要由定平台和动平台及连接平台的4条支链组成。每条支链包括驱动杆和固定杆，一端通过R副与定平台连接，一端通过球副S与动平台相连。支链1，3机构相同，为RUS无约束支链。2，4相同为RRS约束支链。约束支链中的转动副轴线相互平行，无约束支链中的虎克铰一条轴线与该支链的R副平行，另一条轴线与该支链的R副垂直，通过改变驱动杆的旋转角度，来调整动平台的位姿。

图1 2RRS－2RUS并联机构

机构坐标系的建立，如图2所示。定平台A1A2A3A4和动平台B1B2B3B4分别是以R和r为半径的圆台，各支链与两平台的连接点分别为AiBi（i＝1，2，3，4），且均匀分布在圆台的边上。为便于分析，将在定平台的中心O上建立固定坐标系O｛x，y，z｝，X 轴沿着A1A3，Z 轴垂直于定平台竖直向上，Y轴满足右手定则。在动平台中心P上建立动坐标系，w轴沿着Z轴的方向垂直于动平台，u沿着PB1的方向，v轴由右手定则确定。动平台上各球铰中心在固定坐标系中表示为X－Y′－X′′，各支链中的驱动杆和固定杆长分别为li1和li2，驱动角度分别为αi（i＝1，2，3，4）。

图2 螺旋坐标系

如果只考虑2，4支链，动平台可以进行X，Y，Z轴方向的移动和绕X，Y轴方向的转动，但由于1，3支链中第2个转动副的约束作用，动平台沿Y轴方向的移动受到限制，最终在4个支链的约束下，该机构具有二维移动和二维转动，X，Z轴方向的移动与绕X，Y轴方向的转动。

2 完整及齐次量纲雅克比矩阵的建立

2.1 约束子矩阵的建立

根据螺旋理论，将动平台的瞬时速度用＄p＝［wTvT0］表示，w为动平台的角速度，v0为动平台上瞬时速度与定坐标系原点相重合的那一点的线速度矢量。瞬时速度，可以通过各支链的瞬时螺旋运动线性叠加得到：

由图2可知，1，3支链的各关节的运动螺旋，即

2，4支链的各关节的运动螺旋为：

ai为点Ai相对于O的位置矢量；bi为点Bi的位置矢量，即bi＝RBi；ci为点Ci的位置矢量，即ci＝bi＋li2wi2；sij为第i条支链的第j个转动副的单位方向向量。

根据螺旋理论，可以找到与每条支链的5个运动螺旋都互逆的运动反螺旋，其反螺旋在该并联机构中的描述为与各支链中所有转动副（R副）共面的运动螺旋［1］。

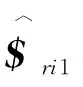
将式（4）与式（1）做互易积得：

将上式写成矩阵形式为：

Jc为约束子矩阵，由于2，4支链所采用的是虎克铰，所以在动平台运动过程中，并没有提供约束，也就是说只有1，3链有约束子矩阵。

2.2 运动子矩阵的建立

式（8）与式（2）做互易积，得：

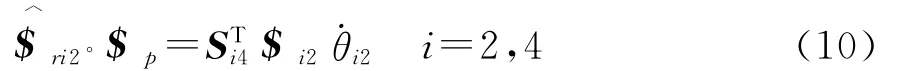
式（9）与式（2）做互易积，得：

联立式（10）和式（11），得到：

2.3 完整雅克比矩阵的建立

将运动子矩阵和约束子矩阵联系起来即得到完整雅克比矩阵。即联立Ja和Jc，得完整雅克比矩阵为：

3 齐次量纲雅克比矩阵

雅克比矩阵的使用条件是受限的，只有机构中只存在移动或转动时才可使用，而齐次量纲雅克比矩阵的条件数可以运用到有着复杂运动（同时包含转动和移动）的机构中。

首先在坐标O点建立一个参考坐标系R，在O′1个固定坐标系R0和1个瞬时坐标系R′，ei，j表示在点pi处，沿着轴j的单位向量，如图3所示。

图3 平台坐标系的建立

将平台P点相对于O′的速度表示出来，即

v为P点的线速度；w为P的角速度；ri为P到O′的距离。

然后用ei，j对上式两边分别进行点乘，得：

ei，j0＝RTeij，ri0＝RTri为R0相对于R′在R 坐标系下的单位向量，＄ij0为在R0坐标系中的节距为零的单位力螺旋，表示沿ei，j0方向指向P点的单位力。

然后利用四面体构造齐次量纲雅克比矩阵，根据四面体的特点建立5个点，借用四面体的底面（三角形）P1，P2，P3，P4的3个顶点和中心点，再加上四面体的顶点构成5个点。O′为底面的中心，分别为四面体的4个顶点，ri0是顶点Pi到O′的距离，每个顶点都由3组正交轴组成，分别是ei，10┴ei20，ei，10┴ri0和ei，20┴ri0（i＝ 1，2，3，4），其构建图形如图4所示。

图4 四面体坐标系的建立

由此得到如下向量：

βi为ri（i＝1，2，3）与x轴之间的夹角；r为ri的长度。

式（15）可以写为：

Jp0＝［＄0，10＄0，20… ＄4，10＄4，20］T，vp＝［v0，1v0，2… v4，1v4，2］T。Jp0是 一 个 11×6的矩阵，对2RRS－2RUS的4自由度机构来说，可以从Jp0中选取4组线性相关的行向量组成一个4×6的矩阵Jpa0。

然后再由线性映射关系L：＄t∈R6→vpa∈Rf，可以得到：

Jpa便是所求的4×4的4自由度的齐次量纲雅克比矩阵。

Jpa0只与ri0和ei，j0有关。

4 运动学性能评价指标

4.1 条件数

衡量机构运动性能的指标称之为灵巧度。目前衡量机器人灵巧度的指标有2类：一是雅克比矩阵条件数，二是可操作度。使用条件数作为衡量灵巧度的指标。

雅克比矩阵条件数是机构输入速度相对偏差的放大因子，决定了其求逆的计算精度和稳定性，所以在机构设计中要求条件数在操作范围内越小越好，当条件数为1时，机构处于最佳的运动传递性能，其所对应的点具有各向同性点，在位型上称之为运动学各向同性；而当条件数处于无穷大时，机构处于奇异位置。

齐次量纲雅克比条件数，采用矩阵的谱范数表示为：

σmax为齐次量纲雅克比矩阵Jpa的最大奇异值；σmin为齐次量纲雅克比矩阵Jpa的最小奇异值。

给定2RRS－2RUS机构的结构参数l11＝l21＝l31＝l41＝135cm，l12＝l22＝l32＝l42＝170cm ，R＝120cm，r＝80cm。机构齐次量纲雅克比矩阵的条件数。关于姿态角的分布规律，机构条件数关于位置的分布规律，如图5和图6所示。

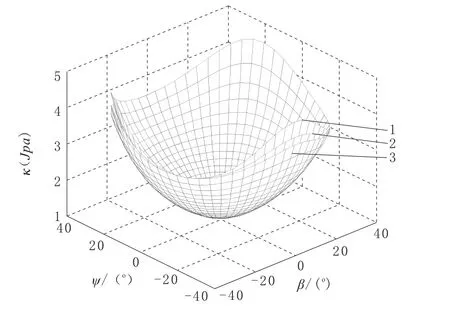
图5 2RRS－2RUS机构Jpa的条件数分布

图5中，1为x＝0m，z＝0.25m；2为x＝0m，z＝0.55m；3为x＝0m，z＝0.75m。

图6 2RRS－2RUS机构Jpa的条件数分布

图6中，1为ψ＝0°，θ＝0°；2为ψ＝15°，θ＝20°；3为ψ＝30°，θ＝40°。

从图5可看到，2RRS－2RUS的条件数κ（Jpa）随z高度的增加，变化并不明显，即z的值对条件数的影响很小。

观察图6可以看出，随着姿态角角度增大，条件数值变大，即机构的运动能力有所减弱。

4.2 全域均值条件数

由于雅克比矩阵依赖于并联机构的位形，只采用一个位型参数下的条件数作为评价指标，具有局限性，所以为总体评价灵巧度，首先对机构的整个工作空间中的各个位型雅克比矩阵条件数求平均值η，显然η越小机构的运动性能越好，即

St为给定工作空间某一高度截面面积。

为了便于讨论尺度参数对机构操作性能的影响，在给定了动平台中心x，z向移动范围和所需的动平台转角范围，同时也给定了机构的尺寸参数（设计变量）：定平台半径R、动平台半径r和连杆长度li1，li2（各支链对应的固定连杆尺寸相同），用r分别对R 和li1，li2（i＝1，2，3，4）进行归一化处理，得：

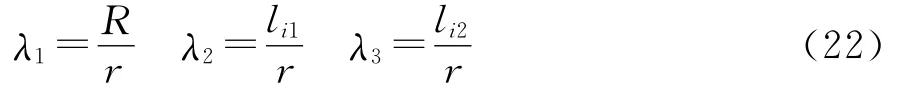
在此，设定参数的变化范围为：λ1＝1～2，λ2＝1～2，λ3＝1～2。然后求出均值条件数随λ1，λ2，λ3的变化规律，如图7所示。

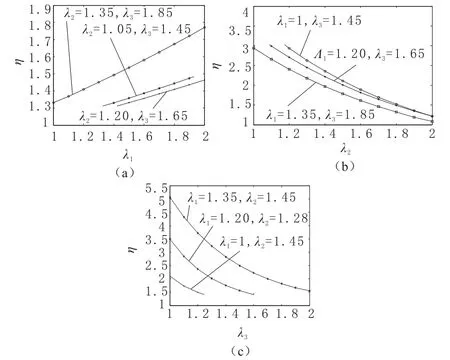
图7 2RRS－2RUS机构Jpa的条件数随λ1，λ2，λ3 的分布

通过观察图7得出如下结论：

a.在给定的范围内，均值条件数随着λ1的变大而增大，其运动性能有所减弱。

b.在参数的变化范围内，均值条件数随着λ2，λ3的变大而减小，其运动能力有所增强。

5 结束语

利用螺旋理论构造出2RRS－2RUS机构完整的6×6雅克比矩阵，可以反映出系统的约束和驱动信息；基于完整雅可比矩阵，可以导出4×4齐次量纲雅克比矩阵；利用齐次量纲雅克比矩阵条件数作为灵巧度指标，分别固定位置参数和姿态参数，得到了齐次量纲雅克比矩阵条件数关于ψ，θ和x，z的分布规律图；以动平台半径为标准对结构参数进行归一化处理，得到了λ1，λ2，λ3，结合全域均值条件数，求得了均值条件数随λ1，λ2，λ3的分布规律，为该机构的进一步优化设计做了贡献。

［1］ 于靖军，刘辛军，丁希仑，等.机器人机构学的数学基础［M］.北京：机械工业出版社，2008.

［2］ 韩书葵，方跃法，槐创锋.4自由度并联机器人刚度分析［J］.机械工程学报，2006，（42）：31－34.

［3］ Joshi S A，Tsai L W.Jacobian analysis of limited－DOF parallel manipulators［J］.Transactions of the ASME，Journal of Mechanical Design，2002，5：341－348.

［4］ 李永刚，宋轶民，冯志友，等.4自由度非完整对称并联机构的完整雅克比矩阵［J］.机械工程学报，2007，43（6）：37－40.

［5］ 黄 府，刘会议.基于雅克比矩阵条件数的并联机构参数优化［J］.设计，2012，39（12）：41－45.

［6］ 胡 波，路 懿.求解3－RPS并联机构刚度的新方法［J］.机械工程学报，2010，46（1）：24－29.

［7］ Kim S K，Ryu J.New dimensionally homogeneous Jacobian matrix formulation by three end－effector points for optimal design of parallel manipulators［J］.IEEE Transactions on Robotics and Automation，2003，19（4）：731－737.

［8］ Sun T，Song Y M，Li Y G，et al.Dimensional synthesis of a 3－DOF parallel manipulator based on dimensionally homogeneous Jacobian matrix［J］.Science China Technological Sciences，2010，53：168－174.

［9］ Liu H，Huang T，Chetwynd D G.A method to formulate a dimensionally homogeneous jacobian of parallel manipulators［J］.IEEE Transactions on Robotics ，2011，27（1）：150－156.