开放进程中人民币汇率间相依性研究——基于动态Copula－GJR－t模型的分析

谢 赤 张 鹏 曾志坚

湖南大学 工商管理学院，湖南 长沙 410082

一、引言

随着全球经济一体化的推进，中国经济正以飞速姿态融入世界经济体系，所面临的外汇风险不断增大。特别是从2005年7月21日起，人民币开始实行“以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度”，加剧了外汇风险的形势。与此同时，近年来国际金融危机频繁爆发，欧美各国汇率出现大幅波动，以美国为首的一些国家为了缓解本国经济恢复与增长的压力，屡次向中国施压，要求人民币升值，将人民币汇率问题推到了风口浪尖，人民币兑美元中间价迭创新高，升值态势强劲，这也加剧了人民币对其它货币汇率的波动。中共十八大报告提出要深化金融体制改革，进一步推进利率市场化和汇率形成机制改革，人民币汇率波动区间将会继续扩大。

在上述背景下，外汇风险对于有关监管部门、金融机构、投资者和涉外企业已经是一种现实存在，加强外汇风险管理刻不容缓。由于外汇风险的有效管理是以外汇风险的准确度量为前提的，而上述有关机构和企业往往持有或投资于多个外汇资产，不同外汇资产之间有着一定的关联，因此要想准确度量外汇组合的风险，必须先对不同货币与人民币汇率间的相依性进行精确刻画。

本文所考察的所谓相依性(dependence)，是基于Copula模型的视角，指有关变量间所有线性和非线性以及对称和非对称相关关系，它不同于以往简单的Pearson线性相关性的思维。Pearson无法刻画变量间非线性和非对称的关系，更无法捕捉到变量间的尾部相依性。与传统相关性相比，本文所指的相依性涉及的考察点更精确、更具体，是对以往相关性概念有关缺陷的克服和相关内容的拓展。

二、相关文献回顾

金融资产间的相依性素来是学术界考察的重点和热点，纵观国内外已有研究，目前对汇率间相依性的研究主要包括三大类。

第一类是以GARCH模型为主体的研究。Laopodis(1998)［1］、Kearney and Patton(2000)［2］运用静态的多元GARCH模型对不同汇率间的相关关系进行了考察。Kitamura(2010)［3］用时变相关的多元GARCH模型研究了欧元、英镑和瑞士法郎兑美元汇率之间的相依性。王昭伟(2011)［4］运用BEKK－MGARCH模型检验了中日韩三国货币汇率的协同波动现象。Kim et al．(2013)［5］建立DCC－GARCH模型对日元与亚洲其它货币汇率间的相依关系进行了研究，发现由于日本和亚洲新兴经济体的积极互动，日元与这些货币联系愈来愈强。

第二类是以VAR方法为基础的协整检验和Granger因果关系检验及其相关拓展。张志波和齐中英(2012)［6］用VAR方法分析了金融危机期间亚洲国家货币的风险传染效应，研究表明，危机期间印尼、马来西亚、韩国和菲律宾的外汇市场受到感染。Nikkinenhe et al．(2006)［7］、Shachmuroe and Shachmuroe(2008)［8］采用 VAR 模型对汇率间的相关关系进行了研究。黄学军和吴冲锋(2006)［9］、代幼渝和杨莹(2007)［10］运用Granger因果关系检验考察了人民币即期汇率与NDF(Non－deliverable Forwards)市场汇率的相依性。Antonakakis(2012)［11］则把VAR模型与GARCH模型结合，对欧元、英镑、日元和瑞士法郎兑美元汇率间的相依性进行了分析。

然而，上述两类方法多从线性、静态相关的角度探讨汇率收益率的相关性，假定汇率收益率的残差服从正态分布，如果样本数据中存在非线性、非正态、尖峰、厚尾等性质，运用这些方法得到的结果就很可能偏离实际。另外，上述两类方法无法刻画极端事件对金融资产相依关系的影响。

第三类是以Copula函数为基础的研究。Copula函数跳出了正态分布假设的束缚，从而避免了不合理的边际分布所带来的模型误差，且能深入地刻画出每一时点汇率间波动的相依性，克服了上述两类方法的缺陷。Patton(2006)［12］、Dias and Embrechts(2010)［13］构建了Copula模型对汇率间的相依结构进行考察，实证结果都发现Copula模型的建模效果优于其它动态基准模型。Diks et al．(2010)［14］采用Copula模型分析了加拿大元、瑞士法郎、欧元、英镑及日元兑美元汇率的相依性，并指出t Copula的建模效果优于其它Copula模型。崔百胜(2011)［15］用藤结构Copula模型考察了欧元兑美元、人民币、港元和日元四种汇率波动间的相依性，但藤结构Copula模型无法刻画出汇率间相依性的动态变化特征。高岳等(2012)［16］运用动态Copula模型对中国主要外汇储备兑美元汇率间的相依结构进行了研究，并指出动态Copula函数仿真VaR可以覆盖最大损失风险。

总体来看，Copula方法有着优于第一类、第二类方法的统计性质，近年来被学者们尝试应用于汇率间相依结构的研究，并取得不错的成果。但迄今为止对人民币汇率相依性的考察还停留在即期汇率与人民币NDF市场之间以及DF市场间，鲜有文献专门探讨汇改后人民币对不同货币汇率间相依性问题，也少见学者对美国次贷危机、欧洲债务危机爆发期间人民币对世界主要货币汇率间的风险传染问题进行深入分析，更没有研究专门考察极端事件下汇率间相依性的变化与股票市场间相依性的变化有何异同，而这些问题对学术研究和实际操作都极具意义。所以，本文运用最新的Copula原理构建了动态Copula－GJR－t模型，从多个角度出发对开放进程中人民币主要汇率间的相依性进行考察。

三、模型构建

(一)边际分布的设定

考虑到金融收益序列大多具有自相关及条件异方差、尖峰、厚尾以及“杠杆效应”，因此本文拟采用ARMA(p，q)－GJR模型对人民币汇率各收益率的波动进行建模，并假设误差形式服从t分布。

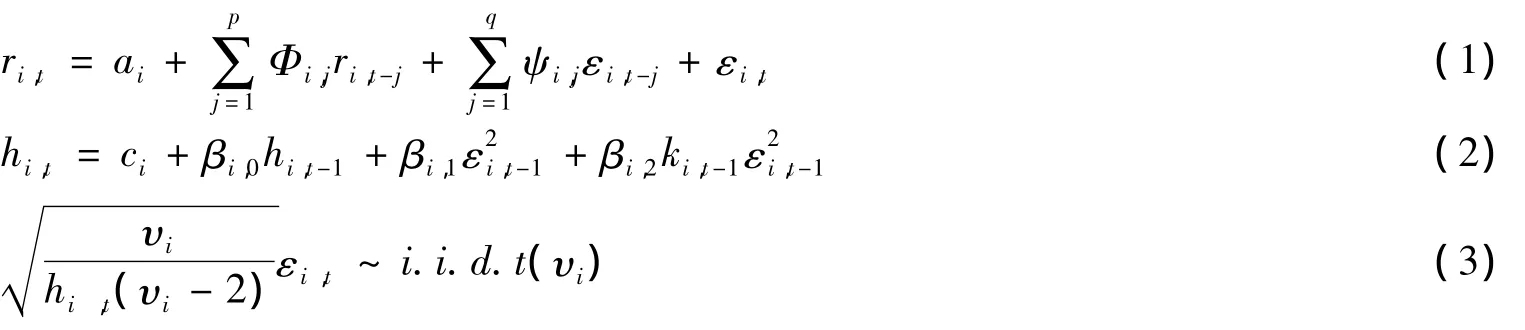
其中，ri，t表示人民币汇率的收益率，ai为截距项，p 是收益率的自回归阶数，Φi，j反映滞后j期的历史收益率对当期收益的影响，q是残差项的自回归阶数，ψi，j反映滞后j期的历史残差对当期收益的影响，εi，t为时刻t的残差，hi，t为时刻t收益率的条件波动率，βi，o+ βi，1+0．5βi，2的大小反映了收益率序列的波动持续性，βi，o是 GARCH 项的系数，βi，1是ARCH项的系数，βi，2反映上一期利空和利好消息对当期收益率波动的影响，用来衡量“杠杆效应”，ki，t－1为虚拟变量，当残差 εi，t－1为负时，ki，t－1=1，否则 ki，t－1=0。

(二)Copula函数的选取

在得到单个变量的边际分布之后，便可选取合适的Copula函数进行相依性建模。本文对人民币兑美元、欧元和日元汇率间相依性考察分为两个层面，第一个层面是对上述汇率间一般情况下的相依性进行考察;第二个层面是对上述汇率间的极值相依性(即尾部相依性)进行考察。对于两收益率间一般情况下相依结构的描述，使用较多的是Gaussian Copula和t Copula函数，为突出本文建模的准确性，本文将在后面的实证中进行对比。

Gaussian Copula的条件密度函数为:

t Copula的条件密度函数为:

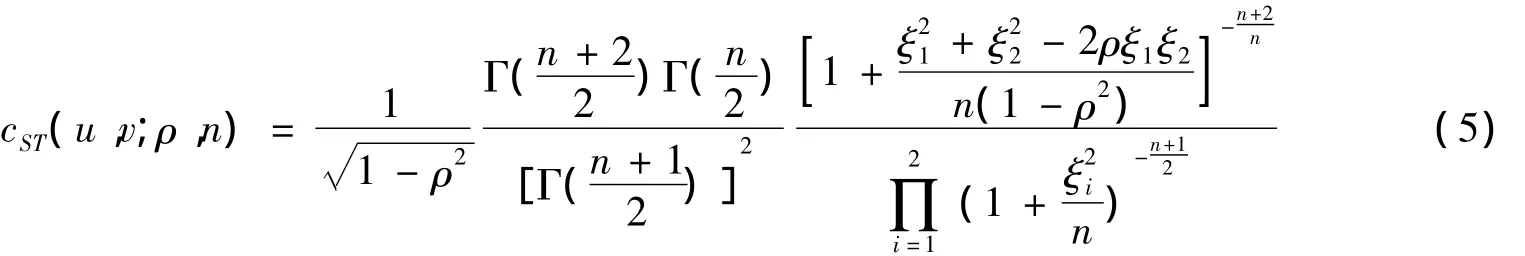
其中，Φ－1(．)是标准正态分布函数 Φ(．)的逆函数(．)是 t分布函数 Tn(．)的逆函数为相依性参数。

尾部相依性包括上尾和下尾相依性。Gaussian Copula因为尾部相依性为零，所以无法刻画，t Copula的上、下尾部相依性相等，而实际金融市场中金融资产间的尾部相依性往往是非对称的，所以它也无法准确刻画。因此，对于第二个层面的考察，本文引入SJC Copula(Symmetrical Joe－Clayton Copula)，它能准确地捕捉金融市场间非对称的尾部相依性。

SJC Copula的函数形式为:

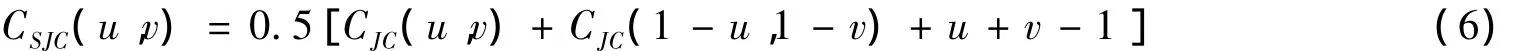
其中，有:

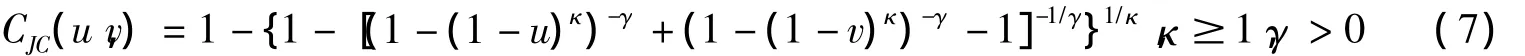
SJC Copula函数的参数与上、下尾部相依性参数有一一对应的关系:

另外，考虑到汇改后人民币汇率处于不断变化的环境中，本文参考Patton(2006)的研究，令Copula中的相依性参数服从动态变化的过程。

其中，Gaussian Copula和t Copula中的相依性参数ρ分别服从如下动态变化过程:

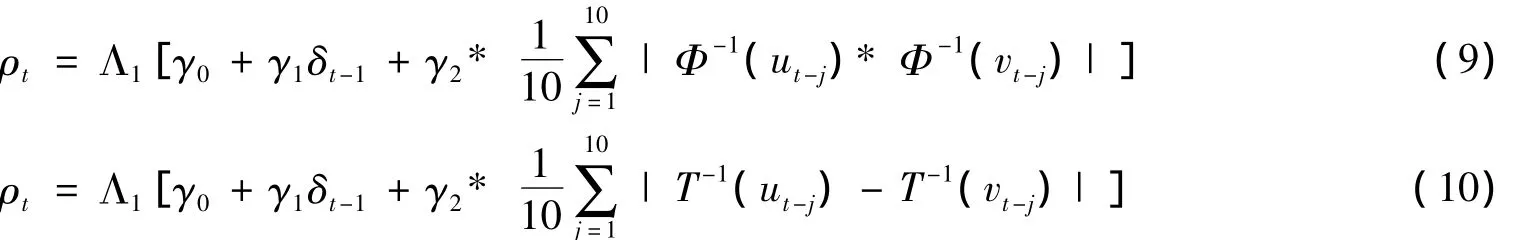
SJC Copula中的上、下尾部相依性参数λU、λL服从如下动态变化过程:

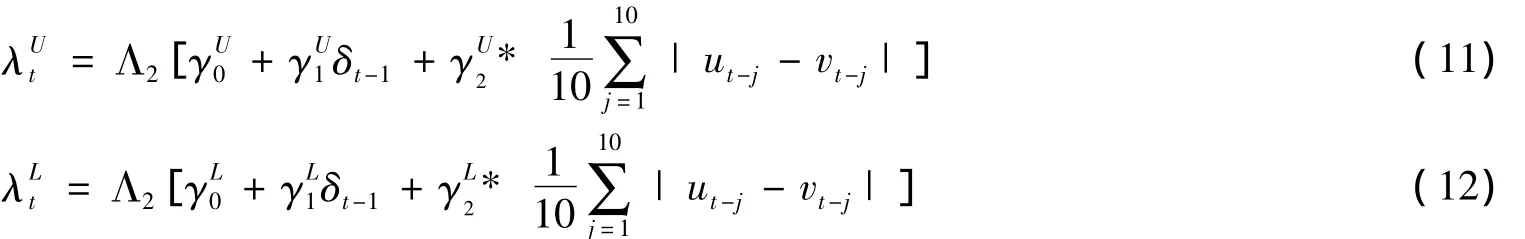
四、实证研究

(一)数据来源及描述性统计

当前，美元、欧元和日元是世界上最主要的三种货币，人民币对这三种货币汇率的波动会对中国经济产生非常重要的影响。另外，由于2005年7月21日以前人民币汇率是盯住美元的，就本文所涉及的研究问题实际意义不大。因此，本文选取2005年7月22日至2013年4月30日人民币兑美元、欧元和日元的每日汇率中间价作为样本数据开展实证研究。数据来源于中国国家外汇管理局，人民币汇率均采用直接标价法。人民币汇率的收益率采取对数收益率:

表1 人民币兑美元、欧元和日元汇率的收益率统计性质描述

由表1可以看出，人民币兑美元、欧元和日元汇率的收益率的均值都为负，这与近年来人民币不断升值的实际情况相吻合。人民币兑美元汇率的收益率的标准差最小，反映了美元作为国际主导货币，有着较好的稳定性。在偏度上，各汇率的收益率序列均表现出不同程度的左偏。在峰度上，各汇率的收益率的峰度显著大于3。另外，由Jarque－Bera统计量来看，所有收益率序列均在1%水平上拒绝正态分布的原假设，说明它们呈现“尖峰厚尾”的性质。对各汇率的收益率序列进行ARCH－LM检验发现，各收益率序列均存在条件异方差性，适合用GARCH模型进行建模。由Ljung－Box统计量可以看出，人民币兑美元、兑日元汇率的收益率存在高阶序列相关。最后，由ADF检验和PP检验结果可知，所有收益率序列的统计量在1%的水平上都显著，说明各收益率序列是平稳的。

表2 人民币汇率序列间的相关性系数的估计

由表2知，人民币兑美元与兑欧元、兑日元汇率的Pearson线性相关系数、Kendall、Spearman秩相关系数都为负，说明整体上人民币兑美元汇率与兑欧元、兑日元汇率的变化趋势相反。人民币兑欧元汇率与兑日元汇率的三种相关系数为正，说明整体上它们呈现出相同的变化趋势。

(二)边际分布的参数估计

经过反复拟合检验，边际分布的具体参数估计结果如表3。

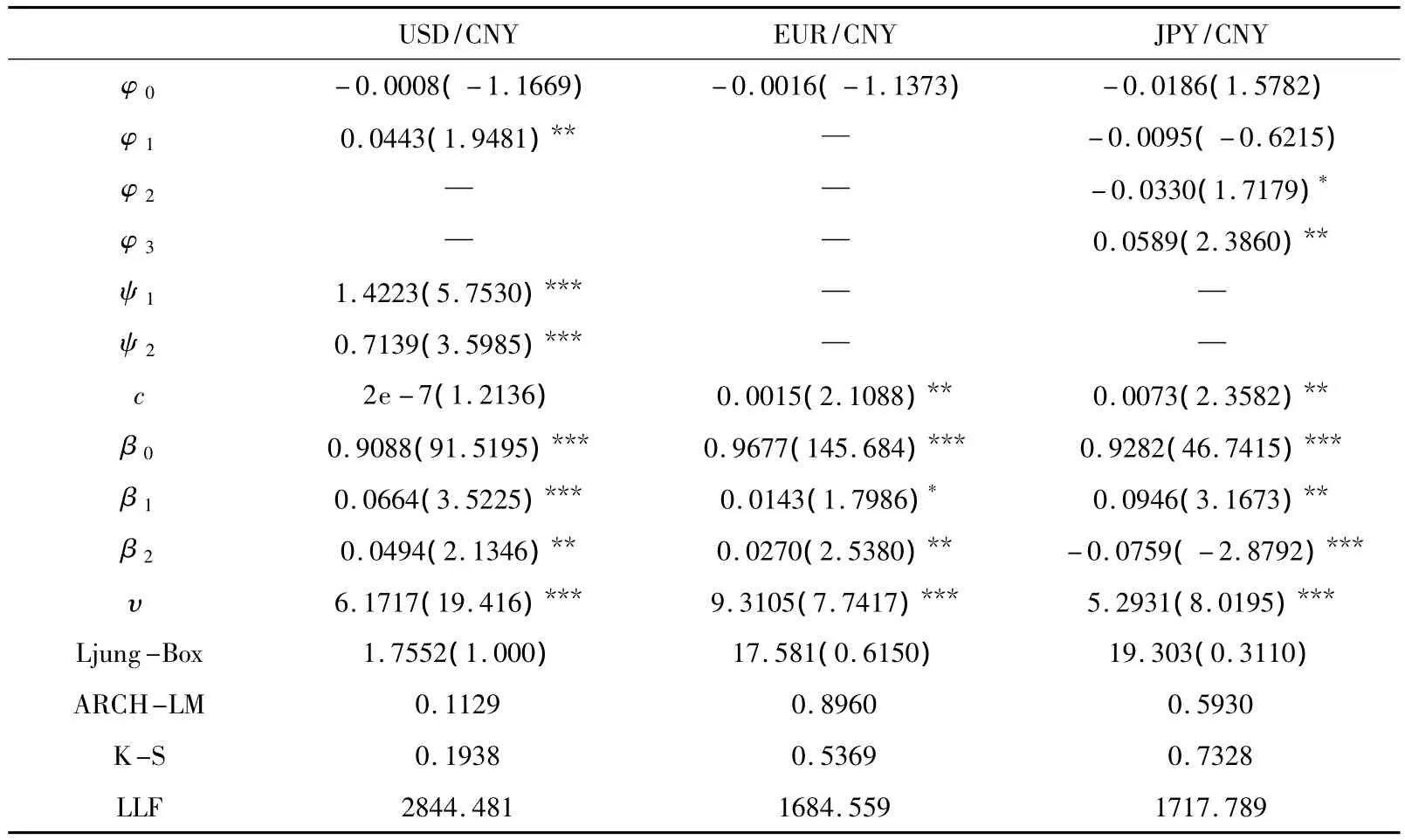
表3 边际分布的参数估计

从Ljung－Box和ARCH－LM的检验结果可知，人民币汇率收益率的高阶序列相关性以及ARCH效应都已被消除。β0+β1+0．5 β2接近于1，表明各收益率序列的波动效应都较持久。从β2来看，它们的t统计量在5%的水平上都是显著的，说明采用GJR模型来估计各收益率序列的条件方差是较为合理的。其中，人民币兑美元、兑欧元汇率的β2值都大于零，说明负向“杠杆效应”明显，人民币升值(εi，t＜0)带来的冲击大于贬值带来的冲击，人民币升值的信息对人民币汇率的波动影响较大;人民币兑日元汇率的β2值小于零，说明正向“杠杆效应”明显，人民币贬值(εi，t＞0)带来的冲击大于升值带来的冲击，人民币贬值的信息对人民币汇率的波动影响较大①负向“杠杆效应”指投资者对利空消息反应强烈，本文中人民币升值是利空消息;正向“杠杆效应”指投资者对利好消息反应强烈，本文中人民币贬值是利好消息。。各收益率的自由度参数υ都集中在4～10之间，并且都在1%的水平上显著，表明各收益率存在明显的厚尾特性。另外，3个序列在5%水平上均通过K－S检验，说明本文的边际分布建模是合理的。

(三)人民币汇率间的一般相依性结果及分析

获得边际分布函数的参数估计值后，便可得到各汇率收益率的累积分布函数值序列u和v，然后利用它们对Copula函数进行参数估计，所得结果如表4。

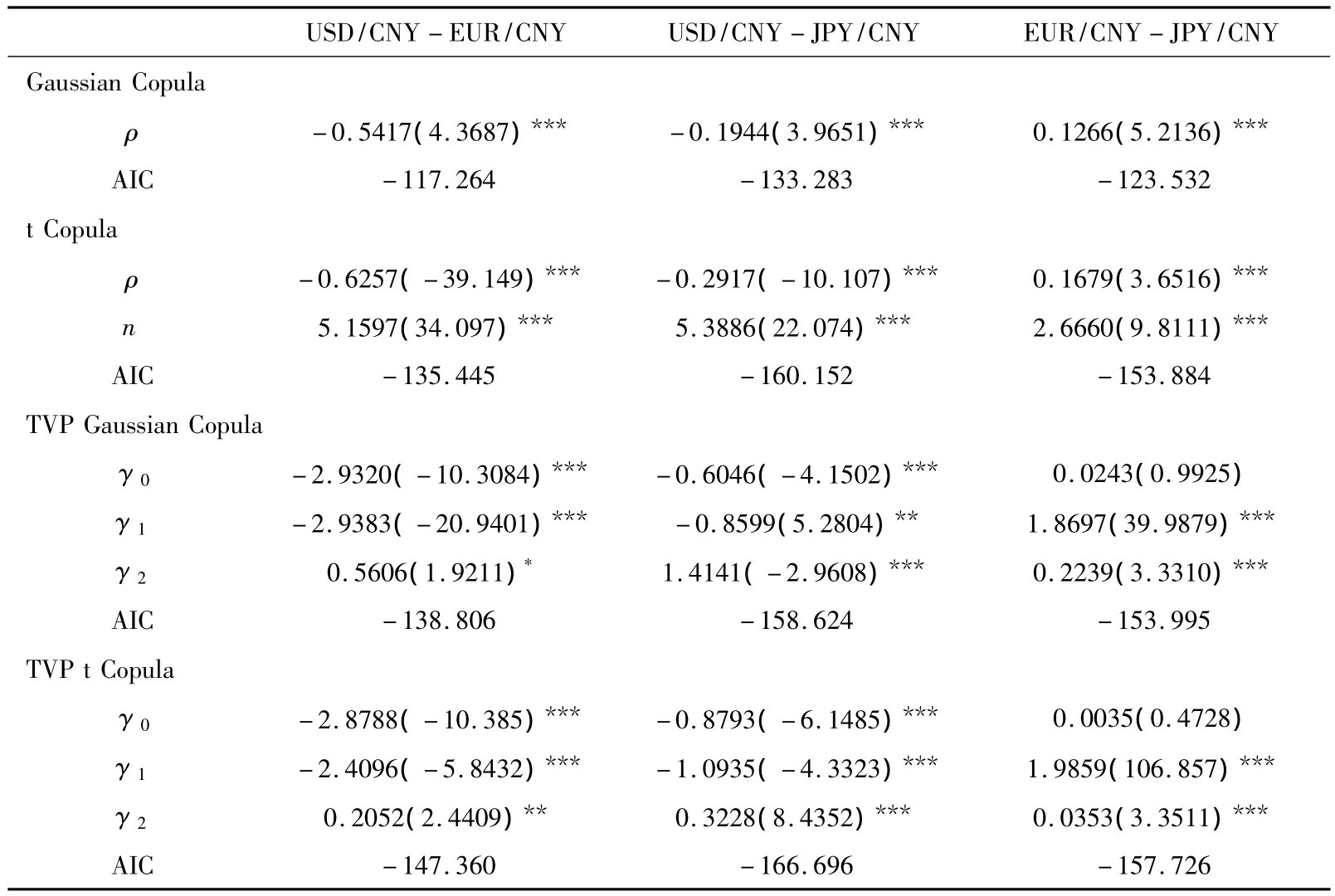
表4 Gaussian Copula和t Copula模型的参数估计

由表4可以看出，TVP t Copula模型所得到的AIC在各组中都是最小的，表明其拟合效果较好。所得条件相依图如图1、图2、图3。

1．从图1、图2、图3可看出，三汇率间的相依性呈现显著的动态性，且与前面所获得的Pearson、Kendall和Spearman相关系数有较大差异，所以用这三个相关系数对其相依性进行刻画是不合适的。人民币兑美元汇率与兑欧元、兑日元汇率都呈现负相依性，且前者的负相依程度较大，这可能是因为美元与欧元、日元所代表的经济体是相互竞争的经济体，美元所代表的经济体与欧元所代表的经济体之间更是竞争激烈。人民币兑欧元汇率与兑日元汇率整体上呈现正相依性，但在某些时点呈现出了强负相依状态，这可能是金融危机等极端事件造成的。同时，它们间的相依性在三者中波动幅度最大，从－0．9～0．6，从侧面反映出人民币主要是盯住美元，人民币兑美元汇率波动幅度相对较小，而人民币兑欧元和日元汇率的波动幅度较大。

2．在美国次贷危机爆发后，人民币兑美元与兑欧元、兑日元汇率之间的负相依程度并没有显著变化，说明次贷危机在初期对两者间相依性并没有显著影响。人民币兑欧元与兑日元汇率间的相依性由正变为负，说明次贷危机对人民币兑欧元和兑日元汇率分别产生了不同的影响。随着次贷危机全面爆发，对三汇率间的相依性也产生了显著影响。

由图1、图2、图3还可以发现，在2008年9月左右，三汇率间的相依性都发生了显著的变化，而这个时期正是“雷曼兄弟”全面破产，全球金融危机爆发阶段。

其中，人民币兑美元与兑欧元汇率的负相依性急剧增强。这可能是因为危机爆发，投资风险上升，大量投资者购买美国国债规避风险，导致美元走强，欧元走弱，欧元对美元汇率大幅贬值，而此时人民币并没有因为美元走强而贬值，人民币盯住美元，因而两者之间的负相依性增强。这点与股票市场间的相依性有很大的区别。在经济动荡或危机期间，股票市场间一般会呈现比较紧密的正相依性。曾志坚等(2009)［17］及庞晓波和李艳会(2010)［18］研究发现在金融危机深化时期，中国股票市场与世界股票市场呈现显著增强的正相依性。Cheung et al．(2010)［19］对2007～2009年全球金融危机期间全球股市间的相依结构进行了研究，发现危机期间美国股市与世界其它股市的正相依性显著增强。

人民币兑美元与兑日元汇率的负相依性也显著增强。这是因为之前一段时期人民币对美元和对日元都是处于升值状态，全球金融危机爆发后，日元并没有像欧元那样对美元贬值，反而对美元升值。究其原因，主要是长期以来，日本维持低利率政策，借款成本较低，所以很多投资者大量借入日元投资到收益率高的其它货币金融资产赚取较高收益。全球金融危机爆发后，经济形势恶化，投资收益下降，投资者迅速平仓，纷纷变卖外国资产偿还日元，导致对日元需求大幅上升，所以人民币对日元大幅贬值。而此时人民币是盯住美元，因而两者之间的负相依性增强。

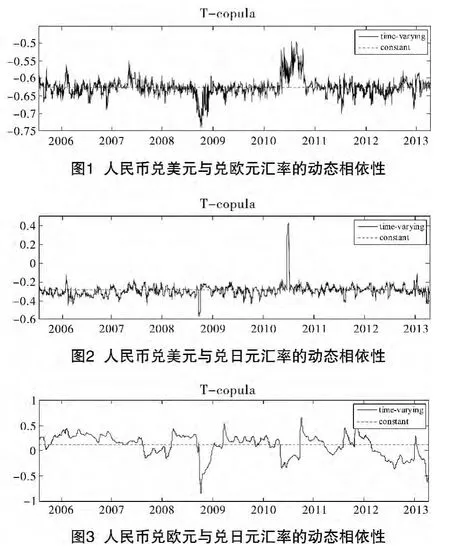
人民币兑欧元与兑日元的汇率在这段时期成截然相反的走势，故它们之间呈现强负相依状态。

3．在欧洲债务危机爆发后，人民币兑欧元与兑美元、兑日元汇率之间的相依性短期内并没有显著变化。但在2010年3月以后，人民币兑欧元与兑日元汇率之间的相依性出现剧烈波动，这可能与欧债危机的影响是蔓延性而不是急剧性有关。

然而，欧债危机的爆发对人民币兑美元与兑欧元、兑日元汇率间的相依性一直没有显著影响。这是因为在这段时期，货币当局为了维护人民币的平稳发展和国内金融环境的稳定，暂停了人民币汇改，人民币转而又回归成单一盯住美元的策略，在一定程度上扭曲了人民币兑美元与兑欧元、兑日元汇率间的相依性。但在2010年中，人民币兑美元与兑欧元、兑日元汇率间的相依性出现一个急剧变化的过程，这可能与人民币二次汇改有关。因为重启汇改后，人民币汇率更大幅度的双向波动开始出现，所以2010年中是人民币兑美元与兑欧元兑日元汇率相依结构变化的一个突变点，它们间的相依性出现急剧变化。

4．在后金融危机时代，人民币兑美元与兑欧元、兑日元汇率间的相依性较平稳，但人民币兑欧元与兑日元汇率间的相依性则是波动剧烈，特别是在2012年以后，它们间的相依性几乎完全趋于负值，在2013年4月，两者的相依性甚至达到－0．6。这可能与该时期日本的宽松货币政策有很大关系，日本政府大量发行日元以刺激经济，导致日元对人民币较大幅度贬值，而这段时期欧元对人民币的汇率则较为稳定。

(四)人民币汇率间的尾部相依性结果及分析

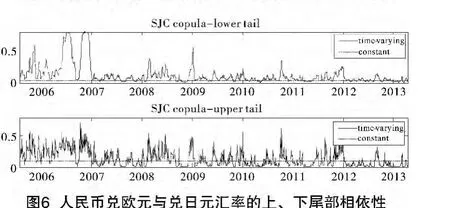
为进一步考察人民币兑美元、欧元和日元汇率间的极端风险传染，本文采用动态SJC Copula对它们间的上、下尾部相依性进行分析，如图4、图5、图6所示。

上、下尾相依性的度量在金融风险管理中十分重要，这两个指标可以直观地反映两个市场间是否存在风险传染关系，即一个市场的大涨(大跌)是否会引起另一个市场的大涨(大跌)。

从图4、图5、图6可知，人民币兑美元与兑欧元、兑日元汇率间的上、下尾部相依性都十分接近于零，说明人民币兑美元汇率与兑欧元、兑日元汇率不存在大幅同涨或同跌的风险传染关系。这可能是因为美元与欧元、日元是竞争的关系，当美元大幅升值(贬值)时，欧元和日元更多的是呈现贬值(升值)的状态。这与股票市场有着显著差异。相比之下，人民币兑欧元与兑日元的汇率间呈现波动较大的上、下尾相依性，说明两者同时大涨或大跌的可能性较大，存在风险传染关系。不过，次贷危机和欧债危机爆发后，两者之间的上、下尾部相依性并没有发生区别于其它时期的显著变化。

五、结论

本文引入Copula函数方法构建动态Copula－GJR－t模型对人民币三种主要汇率间的相依性进行了全面考察，突破了大部分现有研究仅考察汇率间线性相关性或静态相关性的局限，深入刻画和分析了美国次贷危机、欧洲债务危机期间人民币汇率的波动相依性，并对汇率间的风险传染问题进行了探讨。研究结论如下。

1．人民币兑美元、欧元和日元汇率都存在“杠杆效应”。人民币兑美元、欧元存在负向“杠杆效应”，人民币升值的消息对人民币与美元、欧元汇率波动影响较大;人民币兑日元存在正向“杠杆效应”，人民币贬值的消息对人民币与日元汇率波动影响较大。

2．三种汇率间的相依程度具有显著差别。人民币兑美元汇率与兑欧元、兑日元汇率间呈现显著的负相依性，而人民币兑欧元汇率与兑日元汇率既有负相依性也有正相依性，且波动幅度较前两者更大。这表明相对于人民币兑美元的汇率来说，人民币兑非美元货币的汇率有着更大的波动，较能反映市场的真实状况。

3．人民币汇率间呈现出很强的时变、非线性相依性。本文构建的动态Copula－GJR－t模型准确地刻画了这些特征，说明引入Copula模型对人民币汇率相依性进行考察是合理的，这为今后继续对人民币汇率相依性进行更深入考察提供了新思路。

4．三种汇率间的相依性在极端事件下呈现出显著变化，但不是像股票市场那样呈现出更加紧密的正相依性，而是表现为负相依性增强。同时，对尾部相依性的考察发现人民币兑美元与兑欧元、兑日元汇率的上、下尾相依性基本为零，不存在同时大涨或大跌的可能性;人民币兑欧元与兑日元有着波动较大的上、下尾相依性，说明两者存在极端风险传染关系。

5．当前，人民币汇率仍很大程度受美元影响，人民币汇率间的相依性发生了一定程度的扭曲，不能真实反映市场的实际情况。在稳定国家宏观经济的情况下，中国应该逐步开放外汇市场，加快人民币改革的步伐，完善汇率形成机制，使人民币顺应时代的发展，真正国际化和市场化。

［1］Laopodis，N．T．，1998．Asymmetric Volatility Spillovers in Deutsche Mark Exchange Rates，Journal of Multinational Financial Management，Vol．8，No．4:413 －430．

［2］Kearney，C．，and Patton，A．J．，2000．Multivariate GARCH Modeling of Exchange Rate Volatility Transmission in the European Monetary System，Financial Review，Vol．35，No．1:29－48．

［3］Kitamura，Y．，2010．Testing for Intraday Interdependence and Volatility Spillover Among the Euro，the Pound and the Swiss Franc Markets，Research in International Business and Finance，Vol．24，No．2:158－171．

［4］王昭伟．外汇市场的协同波动与联合干预［J］．国际金融研究，2011(6)．

［5］Kim，B．H．，Kim，H．，and Min，H．G．，2013．Reassessing the Link between the Japanese Yen and Emerging Asian Currencies，Journal of International Money and Finance，Vol．33，No．5:306 －326．

［6］张志波，齐中英．基于VAR模型的金融危机传染效应检验方法与实证分析［J］．管理工程学报，2005(3)．

［7］Nikkinenhe，J．，Sahlstrm，p．，and V h．maa，S．，2006．Implied Volatility Linkages Among Major European Currencies，Journal of International Financial Markets，Institutions and Money，Vol．16，No．2:87－103．

［8］Shachmurove，T．，and Shachmurove，Y．，2008．Dynamic Linkages Among Asian Pacific Exchange Rates 1995－2004 International Journal of Business，Vol．13，No．2:101－117．

［9］黄学军，吴冲锋．离岸人民币非交割远期与境内即期汇率价格的互动:改革前后［J］．金融研究，2006(11)．

［10］代幼渝，杨莹．人民币境外NDF汇率、境内远期汇率与即期汇率关系的实证研究［J］．国际金融研究，2007(9)．

［11］Antonakakis，N．，2012．Exchange Return Co－movements and Volatility Spillovers Before and After the Introduction of Euro，Journal of International Financial Markets，Institutions and Money，Vol．22，No．5:1091－1109．

［12］Patton，A．J．，2006．Modeling Asymmetric Exchange Rate Dependence，International Economic Review，Vol．47，No．2:527－556．

［13］Dias，A．，and Embrechts，P．，2010．Modeling Exchange Rate Dependence Dynamics at Different Time Horizons．Journal of International Money and Finance，Vol．29，No．8:1687－1705．

［14］Diks，C．，Panchenko，V．，and Dijk，D．，V．，2010．Out－of－sample Comparison of Copula Specifications in Multivariate Density Forecasts，Journal of Economic Dynamics ＆ Control，Vol．34，No．9:1596 －1609．

［15］崔百胜．基于Copula－vines的欧元汇率波动相关性实证研究［J］．华东经济管理，2011(6)．

［16］高岳，王家华，公彦德．具有时变t－Copula蒙特卡罗方法的外汇储备收益风险度量［J］．系统管理学报，2012(3)．

［17］曾志坚，徐迪，谢赤．金融危机影响下证券市场联动效应研究［J］．管理评论，2009(2)．

［18］庞晓波，李艳会．中日两国汇率与股价指数的联动性分析［J］．现代日本经济，2010(2)．

［19］Cheung，W．，Fung，S．，and Tsai，S．H．，2010．Global Capital Market Interdependence and Spillover Effect of Credit Risk:Evidence from the 2007－2009 Global Financial Crisis，Applied Financial Economics，Vol．20，No．(1－2):85－103．