时间分数阶倒向扩散问题的全变分正则化

张维，严春梅

(成都理工大学管理科学学院，四川成都610059)

0 引言

近年来，倒向扩散问题引起了许多学者进行讨论.与经典的扩散模型进行对比，倒向扩散模型有许多不同的性质.比如带有长尾分布的质量传送就不能由经典的扩散模型来描述，这时候就需要用分数阶导数代替经典的时间导数，时间分数阶导数具有记忆效应的缓慢扩散，缓慢扩散最早是由Adams E.E和Gelhar L[1]提出.因为分数阶导数是非局部的，倒向扩散问题是不适定的，相对于时间是不可逆的，向前扩散过程的过度光滑作用使其对不连续的初始状态重建困难.Liu J J和Yamamoto M对分数阶倒向问题做出了研究[2]，倒向扩散模型在图像修复方面有广泛的应用，修复图像的核心是用不连续的图像灰度描绘图像边缘，然而，经典的扩散模型忽略了图像模糊的记忆效应，因此我们引进缓慢扩散模型.

考虑一个时间分数阶倒向扩散模型

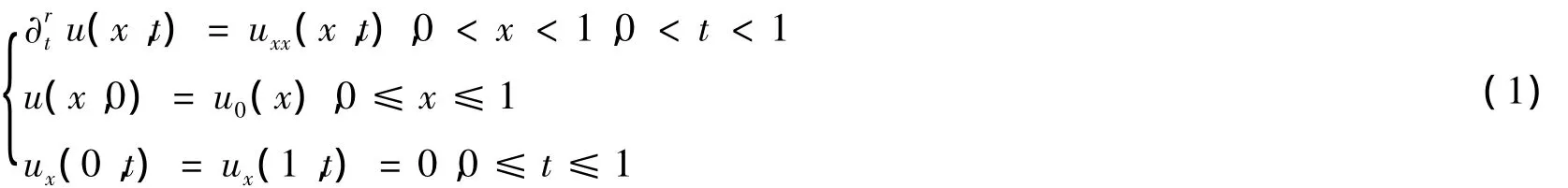
其中r∈(0，1)是关于时间的分数微分阶数，u0(x)是Ω上的有界凸子集，是初始时刻的值.方程(1)中是Caputo导数定义下的分数阶导数，

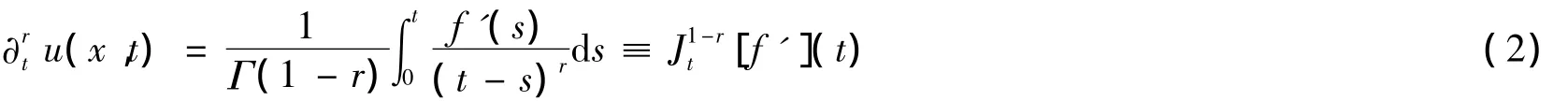
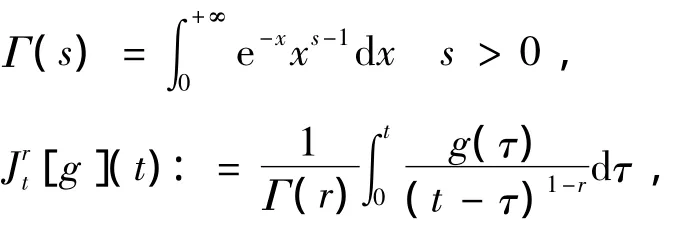
倒向问题是由带噪声的终端数据gδ(x)来反演初值u(x，0)=u0(x)，假设噪声数据满足

δ＞0是误差水平，g(x):=u(x，T)为终点时刻的观测值.由Parseval等式，对式(1)中x作傅里叶变换有

再对式(4)中t做拉普拉斯变换有

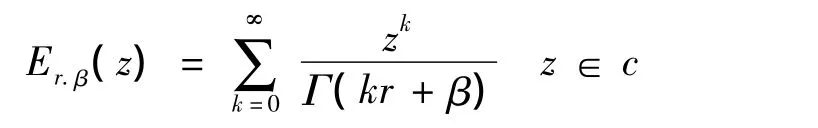
其中r＞0，β∈R是任意常数.

因此，我们由式(5)建立了u(x，0)与u(x，T)之间的关系式.

Er.1是Mittag-Leffler函数，定义如下

1 分数阶倒向扩散的全变分正则化

我们将式(5)中u0进行全变分正则化表示为

约束条件:

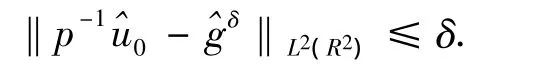
A为一些可容许的近似解.

用拉格朗日公式将式(6)化为无约束的最优化问题

本文将式(1)的近似解转换为求解式(7)最优化问题，下面我们将讨论式(7)解得存在唯一性及稳定性.

定理1 存在唯一性.设A在L1(Ω)上的闭的凸子集，对于∀λ＞0，最优化问题(7)在A上存在唯一极小元.

证明要证明定理1，需要引进引理[3]，引理如下:假设C是Lp(Ω)中的一个闭的凸子集，1≤p≤的线性有界算子，假设K1≠0，1函数被定义为

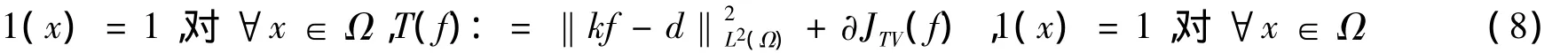
在C上存在唯一极小元.定理1的详细证明见文[4].

定理2 稳定性

1)一致BV强制:对任意子列un∈Lp(Ω)，当lim‖un‖BV=+∞时，有

2)稳定性:在BV有界集中Jn→J一致收敛，等价于给定B＞0，ε＞0，存在N，st当n＞N，‖u‖BV≤B时，

证明因为Jn(un)≤Jn()，由式(10)得

因此由式(9)知，子列un是BV有界的，假设式(11)中=u≠，由J的弱下半连续性质可得:

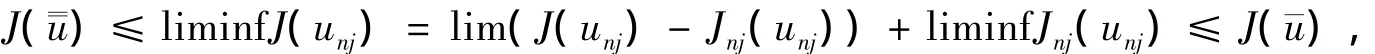
这与定理1中J存在唯一极小元矛盾，即得证.

2 相关的迭代方法

本文用两种计算方法求解问题(7)，分别为Bregman迭代和分离的Bregman迭代方法.

2.1 Bregman迭代

正如上文所述，Bregman迭代最初是由Osher在图像处理中所介绍的[5]，Bregman迭代求解式(7)近似解时，迭代的次数少并且对参数λ是不敏感的，当正则化参数很难选取时，Bregman迭代提供了一个可行的数值解.

凸函数J(·)在点u和v的Bregman距离定义如下:

其中p是J(·)在点v处的次梯度.

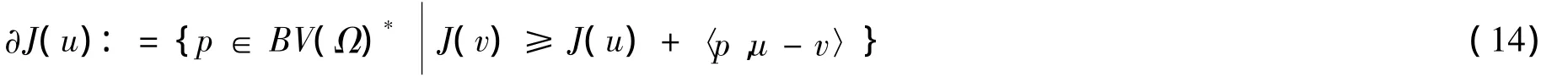
为了求解最优化问题(7)，当u0=p0=0时，文[4]给出了详细的计算过程并进一步得到以下迭代步骤:

当然迭代的收敛率也在文[4]中有详细的叙述，这里就不赘述了.

2.2 分离的Bregman迭代

由Bregman迭代公式我们可以求解(7)的近似解，那么下面我们将用分离的Bregman迭代方法快速地求解式(7)的近似解.

对于式(7)，我们提出分离的Bregman迭代构想，

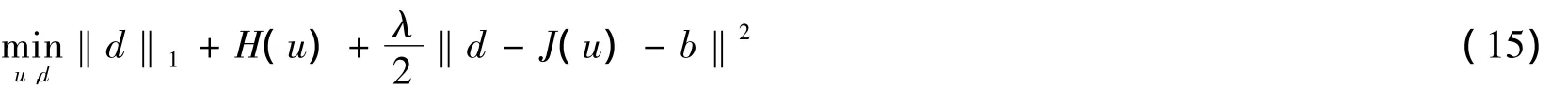
文[6]已经证明了式(15)与式(7)是等价的，我们就可以用下面的迭代公式求解最优化问题:

这时，我们需要解决以下3个步骤，

第3步:bk+1=bk+J(uk+1)－dk.

首先在第1步中，由于耦合性，这是一个关于u的最优化问题是可微的，那么可以直接用傅里叶变换，Gauss-Seidel，共轭梯度法求解.

在第2步中，可以通过软阀值算子有效的求解

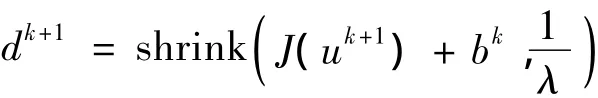
在第3步中已经明确给出了迭代式子，可以直接求解.

通过文[7]我们可以明确得出分离的Bregman迭代方法在计算机中的算法实现，以及收敛率的分析[8].

3 结论

本文运用全变分正则化将时间分数阶倒向扩散问题的不适定性适定化，讨论了最优化问题解的存在唯一性以及稳定性，给出两种迭代方法对最优化问题的解进行数值计算，并且保证了收敛率.

[1] Liu J J，Yamamoto M.A backward problem for the time-fractional diffusion equation[J].Appl Anal，2010，89(11):1769-1790.

[2] Adams E E，Gelhar L W.Filed study of dispersion in a hetero-geneous aquifer 2 spatial moments analysis[J].Water Resour Res，1992，28(12):3293-3307.

[3] Acar R，Vogel C R.Analysis of bounded variation penalty methods for ill-posed problems[J].Inverse problems，1994，10(6):17-29.

[4] Wang L Y，Liu J J.Total variation regularization for a backward time-fractional diffusion problem[J].Inverse problems，2013，29(11):115013-115034.

[5] Osher S，Burger M，Goldfarb D，et al.An iterative regularization method for total variation based image restoration[J].SIAM J Multiscale Modelling Simul，2005，4(2):60-89.

[6] Goldstein T，Osher S.The Split Bregman Method for L1-Regularized problems[J].SIAM J Imaging Sci，2009，2(2):323-342.

[7] 贾小宁.基于傅立叶-全变差正则化的图像去卷积算法[D].长春:吉林大学数学研究所，2011.

[8] Cai J F，Osher S，Shen Z.Split Bregman Methods and Framed based Image Restoration[J].SIAM Multiscale Model Simul，2009，8(2):337-369.