改进的三步相位测量轮廓术

马晓航，朱听玲，赵中立，边心田

(淮阴师范学院物理与电子电气工程学院，江苏淮安223300)

0 引言

相位测量轮廓术[1-3]具有测量精度高、测量范围广、对背景和噪声不敏感等优点，被广泛应用于工业检测、机器视觉、生物医学和实物仿形等领域[4-9].近些年，相位测量轮廓术在三维面形测量中发展迅速，其理论已经相当成熟.通常采用定步长相位测量轮廓术[6，8]来测量物体的三维面形.定步长相位测量轮廓术要求投影到物体表面上的光栅每次移动相等的步长，而且总步长之和为2π的整数倍.该方法对步长相等相移的条件要求较高，在实际测量中很难达到此条件，因此对被测物体面形的恢复具有一定的难度.高成勇[10]等人提出三步非等步相位测量轮廓术，降低了相移条件严格的问题;刘玉凤[11]等人改进了三步非等步相移测量轮廓术，避免了在计算物体的截断相位时由光强相除导致的盲点而使相位计算出错的问题.

本文提出了改进的三歩相移算法恢复被测物体的三维面形，针对相位测量轮廓术系统，采用主动控制相移量，推导出相位求解公式，计算出被测物体的三维面形.通过计算机仿真实验表明，提出的方法具有较高的测量精度和可行性.

1 测量原理

相位测量轮廓术系统原理如图1所示.当一帧正弦光栅图像投影到三维漫反射物体表面上时，由于受物体高度的调制，通过成像系统获得变形条纹图像可表示为

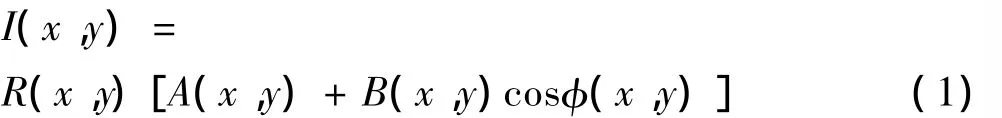
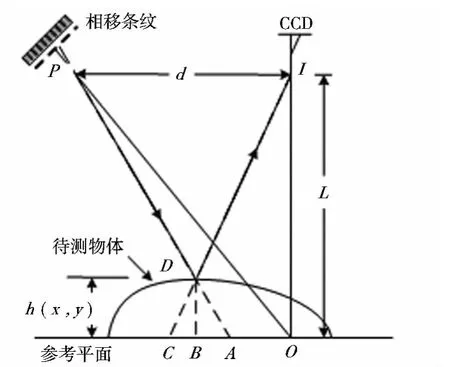
图1 相位测量轮廓术原理图

式中，R(x，y)表示物体表面不均匀的反射率，A(x，y)表示背景强度，B(x，y)/A(x，y)表示条纹的对比.相位函数φ(x，y)表示了条纹的变形，与待测物体的三维面形有关.

连续投影3帧具有相移的正弦条纹，相邻两帧条纹的相移量为α，所产生相应的3帧变形条纹图像可表示为

其中，α⊂(0，2π)，联立式(2)、(3)、(4)，可以计算出相位函数

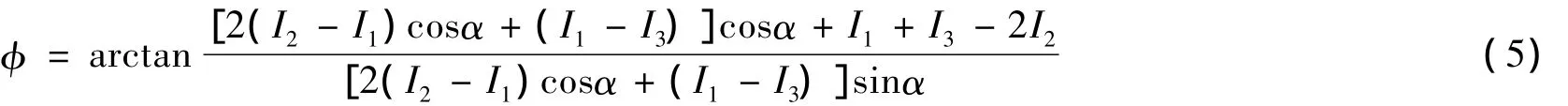
由式(5)计算出的相位分布φ(x，y)被截断在反正切函数的主值范围内，因而此时的相位是离散的，为了从相位函数计算被测物体的高度分布，必须将截断的相位恢复成连续的相位分布φu(x，y).

一般情况下，采用发散照明的相位测量轮廓术系统，其相位与高度h(x，y)之间的映射关系[12]为

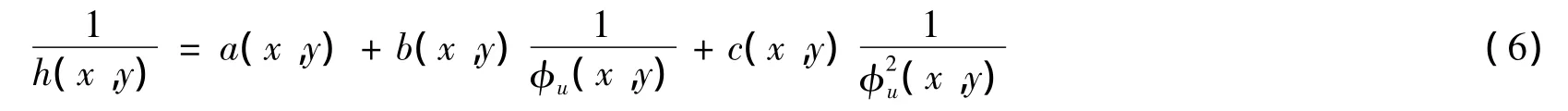
式中，参量a(x，y)，b(x，y)，c(x，y)可以通过标定获得，在投影条件不变的情况下，式(6)中的系数a(x，y)，b(x，y)，c(x，y)是不变的，利用相位分布φu(x，y)与高度h(x，y)之间的映射关系就可以计算出待测物体的三维面形.

2 计算机仿真

图2 模拟物体

图3 变形条纹图

为了验证提出方法的可行性，进行了计算机仿真实验.用计算机生成大小为512×512pixel的peaks函数图像，高度为4 cm，如图2所示.测量系统的几何参量:L=900 mm，d=270 mm，光栅周期为28pixel.CCD采集到受物体高度调制后的变形光栅图像如图3所示.利用3帧变形条纹的强度分布，结合式(3)求出物体上各点的相位分布，然后再通过相位展开等计算解调出待测物体的三维面形信息.在模拟中加入4%的随机噪声，利用改进的三步相移法重建出被测物体的三维面形分布如图4所示，测量误差如图5所示.由图5可以看出，本方法具有较好的抗噪性能，在条纹图中加入4%的随机噪声后，测量误差依然保持在0.02 cm以内.

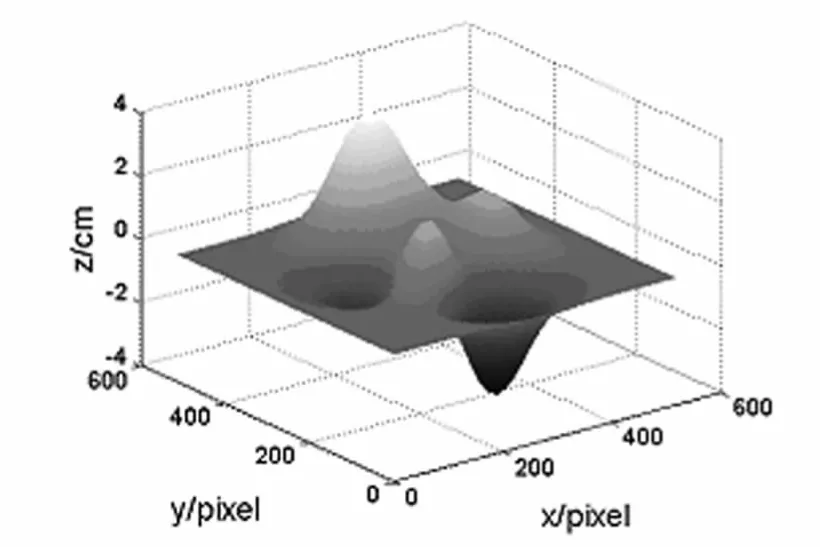
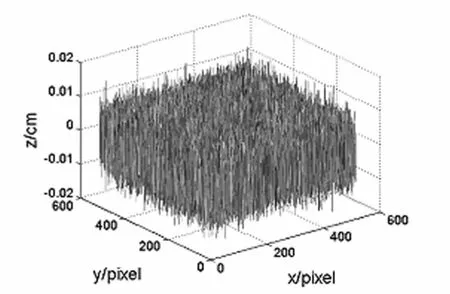
图5 测量误差

通过计算机仿真可以看出，改进的三步相位测量轮廓术能够较好地恢复出被测物体的三维面形，可以应用于三维面形的测量.

3 结论

提出了可控制相移量的三步相移三维面形测量方法，该测量方法只需在3个等相移位置获得3帧受物体高度调制的变形条纹图即可求出相位分布，然后利用相位——高度之间的映射关系即可恢复出被测物体的三维面形分布.计算机仿真实验表明，提出的方法可以很好地恢复出被测物体的三维面形，在很大程度上提高了测量的自动化程度，为产品的在线测量、质量检测提供了一种实用、有效地测量方法.

[1] 肖焱山，曹益平，武迎春，等.相位测量轮廓术中一种快速的系统标定方法[J].四川大学学报:工程科学版，2013，45(1):164-168.

[2] Luo Z Y，Dai J L.Study on an improved five-interferogram phase-shifting algorithm[J].Chinese optics letters，2008，6(5):342-345.

[3] 陈永权，曹益平，常山.非整数倍双频光栅投影的相位测量轮廓术[J].光电工程，2006，33(1):116-119.

[4] 李华伟，申作春，覃银红，等.相位测量轮廓术应用于叶片测量[J].航空动力学报，2012，27(2):275-281.

[5] Zhang S，Yau S T.High-resolution real-time 3D absolute coordinate measurement based on a phase-shifting method[J].Opt Express，2006，14(7):2644-2649.

[6] 喻睿智，曹益平.一种采用相位测量轮廓术的工件在线三维检测方法[J].光子学报，2008，37(6):1139-1143.

[7] 朱林，达飞鹏，盖绍彦.相位测量轮廓术中一种有效补偿相移误差的新算法[J].东南大学学报:自然科学版，2010，40(1):302-307.

[8] Bian X T，Xue J P，Cheng J.Phase measuring profilometry based on elliptically pattern grating[J].2013，124(19):3924-3928.

[9] 赵婧，王永昌，刘凯.一种抑制相位测量轮廓术饱和误差的方法[J].中国激光，2013，40(10):1008001

[10] 高成勇，王蕴珊，周灿林.三步非定步长相移轮廓术研究[J].光电子·激光，2004，15(8):967-970.

[11] 刘玉凤，曹益平，何宇航.新改进型三步非等步相位测量轮廓术算法[J].光电子·激光，2010，21(1):83-86

[12] 苏显渝.信息光学[M].北京:科学出版社，2011.