分数阶微分包含反周期边值问题解的存在性

齐悦

(淮安市高级职业技术学校，江苏淮安223300)

0 引言

分数阶微分方程起源于物理学、人口动力学和经济等研究领域，是人们理解现实世界数学模型的重要工具.因此，分数阶微分方程的研究受到数学工作者的广泛关注.

2012年，Cabada和Wang研究了带有反周期边值条件的分数阶微分方程[4]:

其中0＜p＜1＜q＜2，cDα是Caputo分数阶导数，f是一个连续函数.作者利用Guo-Krasnoselskii不动点定理，研究了带有积分边值的分数阶微分方程(1)的正解的存在性.

受文[4]的启发，在本文中，我们研究如下分数阶微分包含反周期边值问题:

其中0＜p＜1＜q＜2，cDα是Caputo分数阶导数，F:[0，T]×R→P(R)定义在[0，T]上的多值映射.P(R)表示R的所有非空子集.

本文的主要目的是将文[4]的结果扩展到多值情形.我们的结果包含非线性项是凸和非凸两种情形.利用不动点定理研究带有边值条件问题的分数阶微分包含问题(2)的解的存在性.

我们假设读者熟知分数阶微分方程理论和多值映射理论.为方便起见，给出证明主要结果所用的一些常规记号.

对于赋范空间(X，‖·‖)，令

Pcp(X)={Y∈P(X):Y是紧的}，Pcp，c(X)={Y∈P(X):Y是紧凸的}，对于每个y∈C([0，T]，R)，定义F的选择集合为:

SF，y:={v∈L1([0，T]，R):v(t)∈F(t，y(t))对于a.e.t∈[0，T]}

令(X，d)是由赋范空间(X，‖·‖)引进的度量空间.考虑Hd:P(X)×P(X)→R∪{∞}定义如下:

其中d(A，b)=infa∈Ad(a，b)且d(a，B)=infb∈Bd(a，b).显然，(Pb，cl(X)，Hd)是度量空间并且(Pcl(X)，Hd)是一个广义度量空间[4].

令F:[0，T]×R→P(R)是一个带有非空紧值的多值映射，定义与F有关的一个多值算子F:C([0，T]×R)→P(L1([0，T]，R))如下:

下面给出4个引理，它们是证明结论的主要工具，在证明过程中起关键作用.

引理1[4](Kakutani映射的非线性选择定理)令E是Banach空间，C是E的一个闭凸子集.U是C的一个开子集，且0∈.若F:U→Pc，cv(C)是上半连续紧的映射，其中Pc，cv(C)表示的一族非空紧凸子集.则或者

(ii)存在一个u∈∂U及λ∈(0，1)使得u∈λF(u).

引理2[5]令X是一个Banach空间.设F:[0，T]×R→Pcp，c(X)是一个L1-Carathéodory multivalued映射且H是一个由L1([0，T]，X)到C([0，T]，X)线性连续映射，则算子

是C([0，T]，X)×C([0，T]，X)中的一个闭图算子.

引理3[6]令Y是一个可分的度量空间.设F:Y→P(L1([0，T]，R))是一个多值算子，满足F是下半连续且有非空闭的可分解值.则F存在一个连续选择，即存在一个连续单值函数f:Y→L1([0，T]，R)使得对于每个x∈Y有f(x)∈N(x).

引理4[7]令(X，d)是一个完备度量空间.若F:X→Pcl(X)是一个压缩映射，则不动点集F≠φ.

1 主要结果

列出本文的假设条件:

(A1)函数F:[0，T]×R→Pcl(R)是Carathéodory且存在非空紧凸值.

(A2)存在一个连续非减函数ψ:[0，∞)→(0，∞)和一个函数p∈L1([0，T]，R+)使得

(A3)函数F:[0，T]×R→Pcl(R)是一个非空紧的多值映射使

(i)(t，y)|→F(t，y)is L⊗B，

(ii)y|→F(t，y)对于t∈[0，T]是下半连续的.

引理5[4]假设2＜α≤3，0＜p＜1＜q＜2，g∈C([0，T]，R)，则以下问题

存在唯一解

为方便起见，记

定理1 假设(A1)～(A2)成立，若存在一个正数M＞0使得

则问题(2)在[0，T]至少存在一个解.

证明定义算子T:C([0，T]，R)→P(C[0，T]，R)如下:

对于f∈SF，y，我们将证明算子T满足引理1的所有条件.我们将证明分为如下几步.

步骤1:对于每个y∈C([0，T]，R)算子T是凸的.因为SF，y是凸的，易证.

步骤2:T映射C([0，T]，R)中的有界集到有界集.

对于正数r，令Br={y∈C([0，T]，R):‖y‖≤r}中的有界球，则对于h∈T(y)，y∈Br，存在f∈SF，y，使得

并且有

因此，我们有

步骤3:T映射C([0，T]，R)中的有界集到等度连续集.令t'，t∈[0，T]，且t'＜t，y∈Br，其中Br是C([0，T]，R)的一个有界集，对于h∈T(y)，我们有

上式右端不等式当t→t'时趋于0，因此由Ascoli-Arzelá定理，T全连续.

步骤4:T存在一个闭图.令yn→y*，hn∈T(yn)且hn→h*.然后，我们需证明h*∈T(y*).对于hn∈T(yn)，存在fn∈SF，yn，使得

接下来，需证明对于t∈[0，T]存在f*(s)∈SF，y，

考虑如下连续线性算子Φ:L1([0，T]，R)→C([0，T]，R)定义如下:

注意到

当n→∞.因此，由引理2，Φ◦SF是一个闭图算子.另外我们有hn(t)∈Φ(SF，yn).当yn→y*，我们有

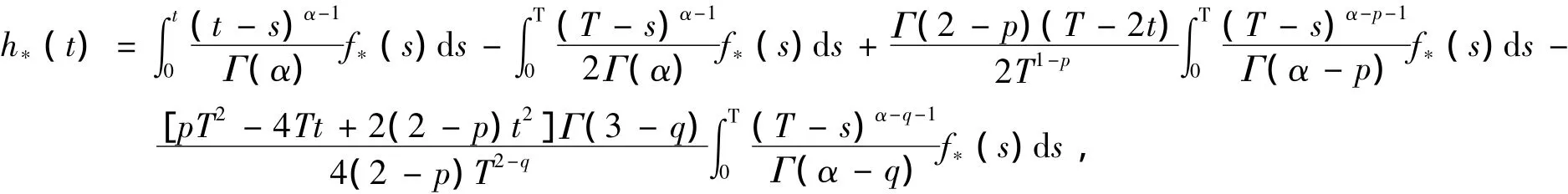
对于某个f*∈SF，y*.

步骤5:存在一个开集U⊂C([0，T]，R)，y∈T(y)对于λ∈(0，1)，x∈∂U令η∈(0，1)，y∈ηT(y).则对于t∈[0，T]存在f∈L1([0，T]，R)，f∈SF，y使得对于t∈(0，1)，我们有

类似步骤2的讨论，我们有

由(4)，存在M使得‖y‖≠M.令

如下讨论，假设F是非凸情形.主要工具为Bressan and Colombo选择定理和带有可分解值的下半连续映射.

定理2 假设(A2)和(A3)成立，并且存在r＞0使得式(4)成立，问题(2)至少存在一个解y.

证明由(A2)～(A3)，F是下半连续型.由引理3，存在f∈C([0，T]，R)→L1([0，T]，R)使得f(y)∈F(y)，对于所有的y∈C([0，T]，R).考虑相应的问题

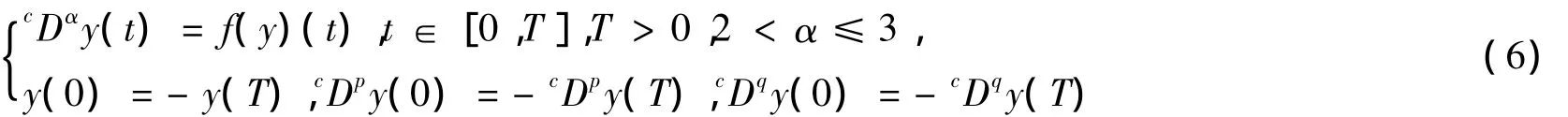
注意到，若y∈C3([0，T]，R)是式(6)的一个解，则y是问题(2)的一个解.为了将问题(2)转化为一个不动点问题，我们定义算子T如下:

容易验证T是连续并且是全连续的.证明余下的步骤类似于定理1的证明，在此省略.

[1] Cabada A，Wang G T.Positive solutions of nonlinear fractional differential equations with integral bound-ary value conditions[J].J Math Anal Appl，2012，389:403-411.

[2] 刘洪洁，赵俊芳，耿凤杰，等.一类分数阶微分方程正解的存在性[J].数学的实践与认识，2012，42(2):241-248.

[3] 王永庆，刘立山.Banach空间中分数阶微分方程m点边值问题的正解[J].数学物理学报，2012，32(1):246-256.

[4] Granas A，Dugundji J.Fixed Point Theory[M].New York:Springer-Verlag，2005.

[5] Lasota A，Opial Z.An application of the Kakutani-ky Fan theorem in the theory of ordinary differential equations[J].Bull Acad Polon Sci Ser Sci Math Astronom phys，1965，13:781-786.

[6] Bressan A，Colombo G.Extensions and selections of maps with decomposable values[J].Studia Math，1988，90:69-86.

[7] Covitz H，Nadler J S B.Multivalued contraction mappings in generalized metric spaces[J].Israel J Math，1970，8:5-11.