一种适合量子计算的素性检验方法

周忠奇

(湖北省煤炭地质局，湖北武汉430070)

0 引言

众所周知，如果m＞1是素数，ordm(a)是正整数a对模数m的阶，则必有

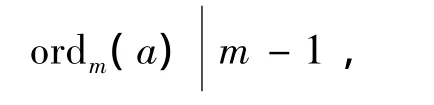
定理 设≥3为正奇数，a为正整数，(a，m)=1，m≠9，15，25，49，561，6601，并设

若k不为整数，则m为合数;若k为整数且k＜9，则m为素数.

证明定理，需要以下引理.

引理1[4]p为奇素数，(a，p)=1，则

引理2[1]如果m=…是m的标准分解式，则正整数a对模数m的阶d=[f1，…，fk]式中，fi表示a对模数的阶.

引理3设m=p1p2p3，其中p1＜p2＜p3，p1，p2，p3为互不相同的奇素数，设

则

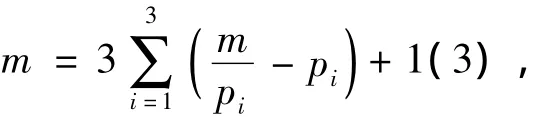
由m=p1p2p3和式(3)知p1，p2，p3都不等于3，且当5≤p1＜p2＜p3，p3≥37时n＜.当5≤p＜p＜p＜37时n≠，所以对于任意不同的奇素数p，p，p，n≠

由m=p1p2p3和式(4)知p1，p2，p3都不等于5.若p1=3，由式(4)有5(p2+p3)+p2p3=7此不可.当7≤p＜p＜p，p≥53时n＜，在7≤p＜p＜p＜53的所有素数中，仅有p=7，p=23， p=41，m=6601使n=3

3＜p2≤7时式(5)不成立.当p2=11时，p3=17，m=561使当p1≥5时，由式(2)

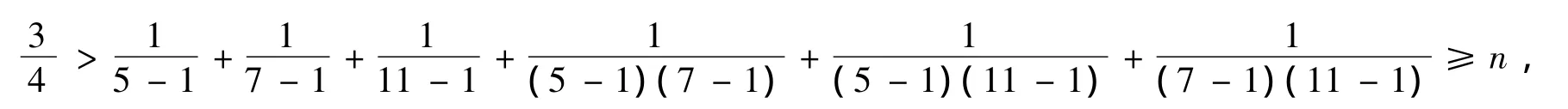
定理 证毕.

引理4设m=p1p2，p1＜p2，p1，p2为不相同的奇素数，若

则

(ii)仅有m=p1p2=7×13=91使

(iii)仅有m=p1p2=3×5=15使

(iv)仅有m=p1p2=5×13=65使

若p1=3，式(7)不成立;若，因p1和p2为不相同的素数，所以若由式(6)

p1=3，5，7时式(8)不成立;若p1=11，由式(8)，p2不为素数;若p1≥13，则所以

当p1=3或5时，式(9)不成立.当p1=7时，由式(9)，p2=13，m=91使当p1≥11时，p2＜11.

若p1=3时，由式(10)，p2=5，m=15使若p1≥5时，由式(10)，可知

若p1=3，式(11)不成立.若p1=5，由式(11)，p2=13，m=65使若p1≥7，由式(11)p2=定理证毕.

引理5设m为奇数若m=9，15，25，49时k不为整数.若m=561，6601时k＞8.

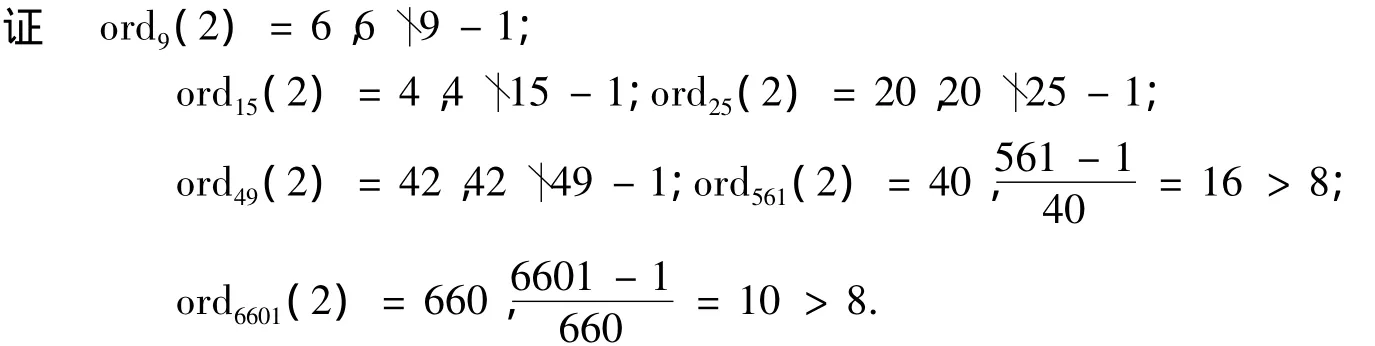
引理得证.

1 定理的证明

若ordm(a)≠m－1，根据引理1，m必为合数.

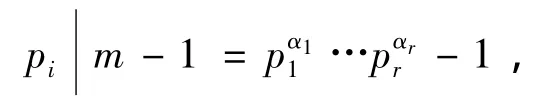
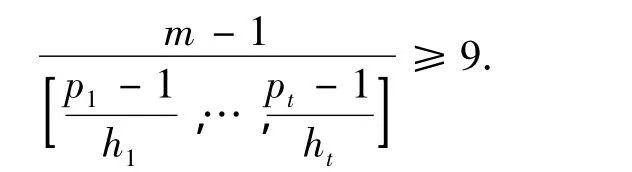
如果t=1，p为奇素数，m=pα且当α＞2时

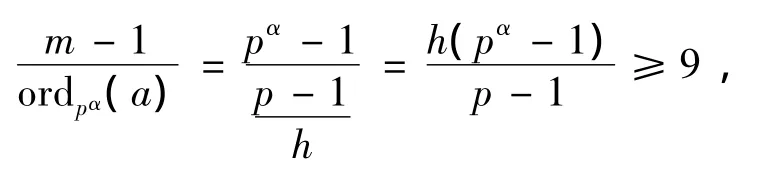
当α=2时

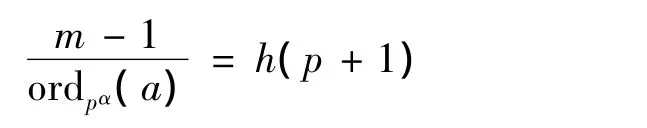
只有在p=3，h=2;p=3，h=1;p=5，h=1;p=7，h=1几种情况下h(p+1)＜9，此时m=9，25，49.所以，当m=pα，m≠9，25，49时

如果m=p1……，pi(i=1，…，t.)qj(j=1，…，s.)均为各不相同的奇素数且ordpi(a)=若t≥1，s≥1，则

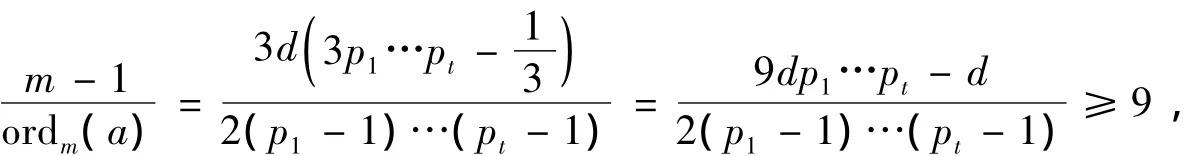
不妨设m=p1…pr，下面要证明的是:如果，则r=1.因

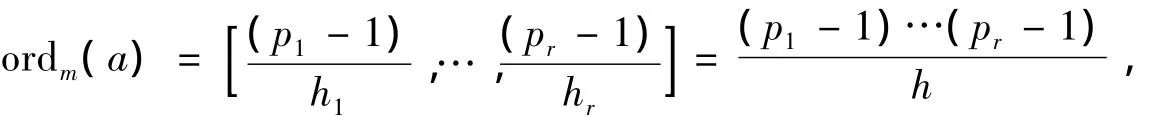
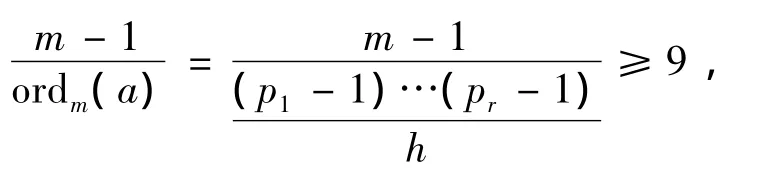
当r=2时，m=p1p2，p1＜p2，p1，p2为不相同的奇素数，

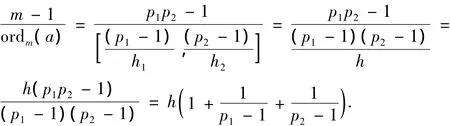
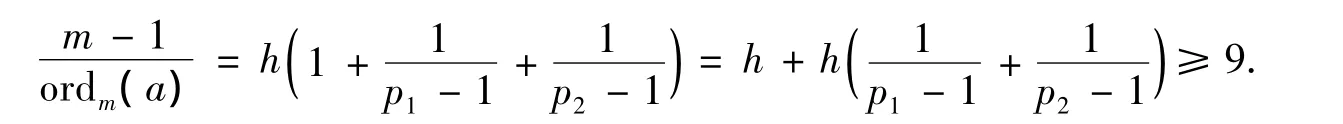
因此，只有h＜8.因p1－1与p2－1均为偶数且

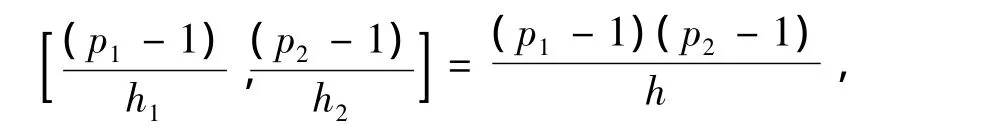
因此，在h中必存在一个因子2，即h＜8的所有可能取值为:2，4，6.因

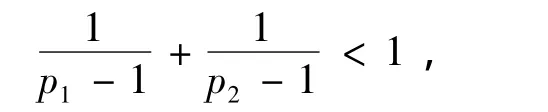
所以只要证明，当m≠9，15，25，49，561，6601时

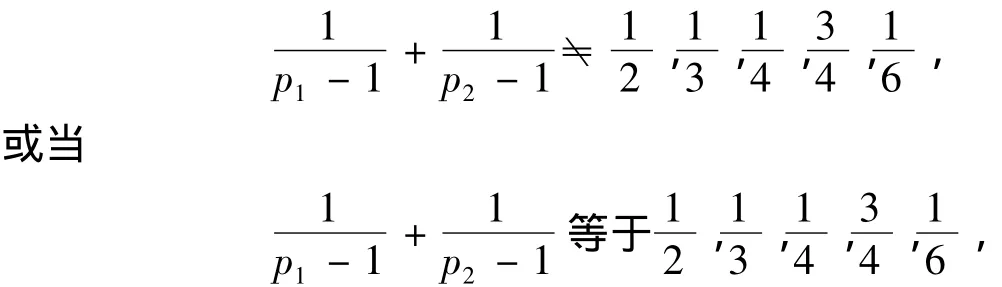
根据引理4知:当m=p1p2，p1＜p2，p1，p2为不相同的奇素数时

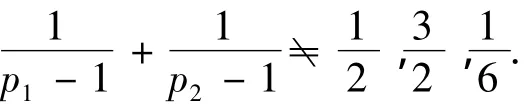
根据引理1和引理2知ord65(a)=[ord5(a)，ord13(a)]的所有可能取值为:1，2，3，4，6，12.所以，若时，m－1=90.

根据引理1和引理2知ord91(a)=[ord7(a)，ord13(a)]，的所有可能取值为:1，2，3，4，6，12，若

所以，当m≠15，m=p1p2且

当r=3时，m=p1p2p3，p1＜p2＜p3，p1，p2，p3为各不相同的奇素数，设

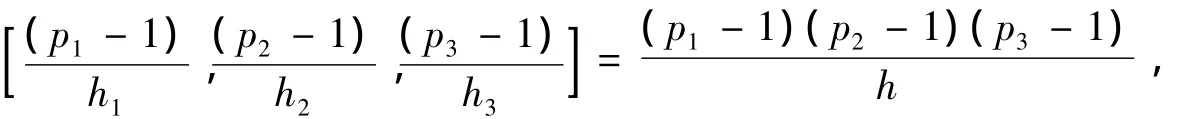
所以在h中必有一个因子4，即h＜8的可能取值只有4，现只要证明，当m≠9，15，25，49，561，6601时

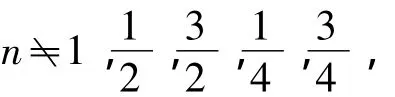
综合以上证明过程得出以下结论:

2 由定理得到的素性检验方法

根据定理，我们可以得到一种确定型一般性素性检验方法:

对于一个奇数m，当m≠9，15，25，49，561，6601时，可以给定一个整数a1＞1，m＞a1，并计算d1=(a1，m)，若d1＞1，则m为合数;若d1=1，再计算ordm(a1)和若k1不为整数，则m为合数;若k1为整数且小于9，则m为素数;若k1为整数且大于或等于9，则再给定一个整数a2＞1，m＞a2≠a1，并计算d2=(a2，m)，若d2＞1，则m为合数;

如果d2=1再计算ordm(a2)和，若k2不为整数，则m为合数;若k2为整数且小于9，则m为素数;若k2为整数且大于或等于9，则再给定一个整数a3＞1，m＞a3≠a2≠a1，…，直到将m判定为合数或素数为止.

实际上，根据引理1.5我们可以设定a1=2从而可以不考虑m≠9，15，25，49，561，6601的因素.下面给出一个判定正整数是否为素数的程序的具体步骤:

1)输入奇数m;a←2;

2)d←(a，m);如果d＞1，则输出合数m.退出;

4)如果k不等于整数，则输出合数m.退出;

5)如果k是整数且k＜9，则输出质数m.退出;

6)a←a+1转到第2)步.

3 结束语

以上的素数检验方法是一种确定型一般性检验方法.通过实际计算可知:用a=2检验一轮便可确定95%以上的数是合数或是素数.例如，a1=2时，在106以内，只有9 538个整数未能确定其素数或合数.

从给出的检验程序可以看出:决定检验时间的主要是求(a，m)和ordm(a)，求(a，m)是可在多项式时间内完成的，但现有计算机求ordm(a)的速度比较慢，但根据资料显示，如果采用量子算法求ordm(a)[5]是多项式时间可完成的，所以，本文给出的应该是一种适合量子算法的素性判别方式.

[1] 柯召，孙琦.数论讲义[M].2版.北京:高等教育出版社，2001.

[2] 颜松远.计算数论[M].杨思熳，译.北京:清华大学出版社，2008.

[3] Ribenboim P.博大精深的素数[M].孙淑玲，冯克勤，译.北京:科学技术出版社，2007.

[4] Joseph H Silverman.数论概论[M].3版.孙智伟，译.北京:机械工业部出社，2008.

[5] 吴盛俊，周锦东，张永德.量子算法简介[J].大学物理，1999，18(12):1-5.